赵春茹，曲军恒，王小龙

(1.梧州学院 信息与电子工程学院，广西 梧州 543002；2.佛山科学技术学院 数学与大数据学院，广东 佛山 528000；3.华南理工大学 数学学院，广东 广州 510640)

0 引言

1 问题和预备知识

1.1问题提出

(1)

假设位势V(x)与非线性项f(x,u)分别满足下列条件：

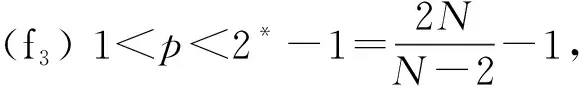
1.2 预备知识

我们注意到方程(1)的解是下列泛函的临界点

(2)

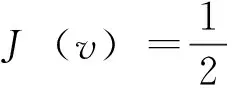
(3)

(4)

非平凡解的存在性。

引理1 设条件(f1)-(f3)成立,对任意的‖v‖=ρ0,存在ρ0,α0>0使得J(v)≥α0.

F(x,s)≤ε∣G(s)∣2+C(ε)∣G(s)∣p+1

且

从而存在一个和ε有关的常数Cε>0,使得

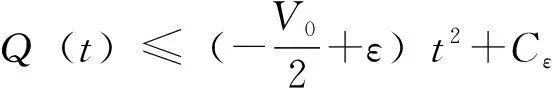
≥C‖v‖2-Cε‖v‖2*

因此，对‖v‖=ρ0，取ρ0>0足够小，使得J(v)≥α0，命题得证。

由(f3)可知,对任意的s>M,存在M>0,使得F(x,s)≥CGμ(s).

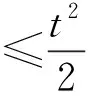
由μ>2知,当t→∞时,J(tφ)→-∞,故命题得证。

由引理1和引理2可知，对常数

c=infsupJ(γ(t))>0

γ∈Γt∈[0,1]

引理3 序列{vn}是有界的。

(5)

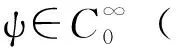
(6)

由条件(f4)知

(8)

由条件(f3)知,F(x,s)CGμ(s)≥CG2(s),s≥1.则

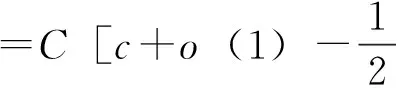
(9)

且由g关于t单调递增，则

(10)

由(f1)-(f3)及Lebesgue控制收敛定理，则

(11)

从而J'(v)ψ=0.

2主要结果

定理1 在条件(V1)、(V2),及(f1)-(f4)下，问题(1)存在非平凡解。

证明：假设v=0,下证{vn}是J∞:H→R的(PS)序列，其中

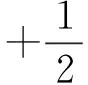
(12)

由(f1)-(f3)知,

则

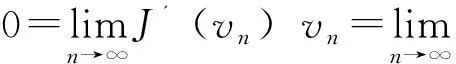
(13)

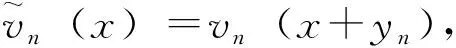
(14)

c∞=infsupJ∞(γ(t))>0,

γ∈Γt∈[0,1]

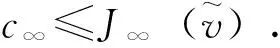
(15)

则由c∞的定义可知

若V(x)≡V∞,则v是非平凡解。假设V(x)

矛盾。从而v是非平凡解。