廉蒙蒙

（安阳工学院机械工程学院，河南安阳455000）

0 引言

边界元法是用于求解工程与科学问题的常用数值分析方法之一，它的基本思想是将经典问题的基本解融入到边界积分方程中，把微分方程的边值问题归化成边界上的积分方程，并以其为控制方程，在借鉴有限元离散的基础上，利用各种离散化技术，通过将边界进行插值离散后，边界积分方程离散为代数方程组,再用数值方法求解代数方程组,从而得到原问题边界积分方程的解[1-2]。边界元法具有边界积分方程非常深厚的数学基础,是继有限元法之后兴起的一种有效的数值方法，这种方法不仅可以用来分析弹性力学等固体力学的问题,同时也可应用于流体力学、声场,以及电磁场等其它的研究领域[3]。

早在1963年M.A.Jaswon[4]首次通过有势的理论对Laplace方程变换，建立了边界积分方程的数值方法，即诞生了间接边界元法，并求解了位势问题。同年G.T.Symm也做了相关的工作[5]。Rizzo在1967年首次提出了直接边界元法，并求解了二维弹性静力学问题，这也是边界元法文献中第一篇关于直接边界元法的文献[6]。关于边界积分方程法的专著是T.A.Cruse和F.J.Rizzo[7]于1975年出版的，并正式的命名此法为边界积分方程方法，这也是边界元中的第一本专著。C.A.Brebbia[8]于1986年编著了《工程师用的边界单元法》，全面详细地介绍了边界元法的原理和应用，并讨论了位势问题和二维弹性静力学力学问题在边界元方法中的应用，并用FORTRAN语言编辑的程序来数值模拟相关问题，这标志着边界元方法已进入了系统性的研究。

1 边界积分方程

边界元法中运用Betti功能互等定理，得到著名的Somigliana等式，即区域内点Y位移的积分表达式[9]

当Y→Γ时，得到弹性静力学的位移边界积分方程

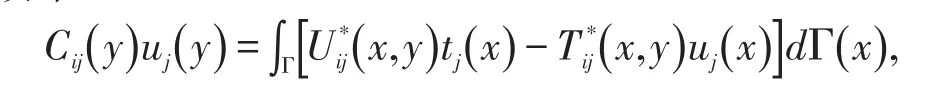
式中 ∫Γ(∙ ∙ ∙)dΓ为沿边界积分的Cauchy主值积分，x和y分别表示边界上的场点和源点，如图1所示。Cij(y)称为位移奇异系数，它依赖于边界Γ上y点附近的几何形状与弹性常数，对于光滑的边界点处，Cij=δij2。但是在实际的计算中，并不是直接计算这一系数，而是通过刚体位移求得。uj(x)和tj(x)分别表示边界Γ上的位移分量和面力分量；Ui∗j(x,y)，Ti∗j(x,y)为边界积分方程的核函数，亦称为基本解，它们分别表示在无限弹性平面的一点y(源点)的i方向作用单位集中力时，在边界上ui任意一点x(场点)的j方向上产生的位移和面力。对于平面应变问题它们的具体形式为[10]

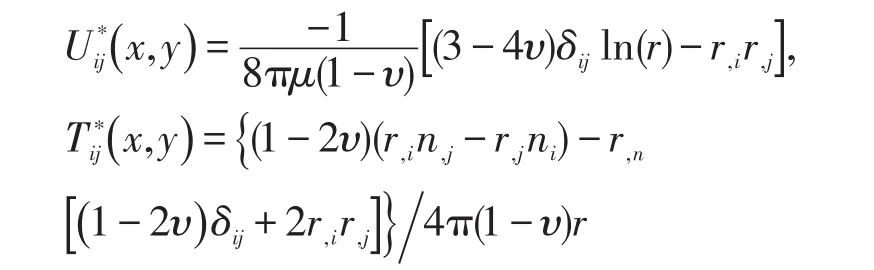
式中，令xi和yi分别为场点和源点的坐标,则源点y到场点x的矢径r→定义为

采用线性单元离散边界积分方程后，可以写成

把各节点的位移与面力分别记作单元位移矢量{u(e)}和单元面力矢量{t(e)}

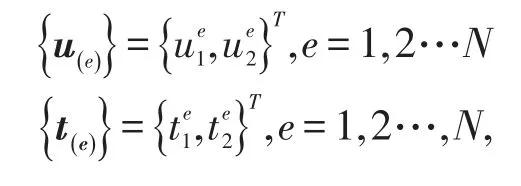
2数值计算

例：受均匀压力P=1的狭长薄板，如图2所示，狭长板沿x轴的长度为L=2m，板的厚度h在1～10-10m之间变化，板的弹性剪切模量μ=8.0×1010Pa，泊松比υ=0.2，当y=0时，边界条件ux=uy=0。

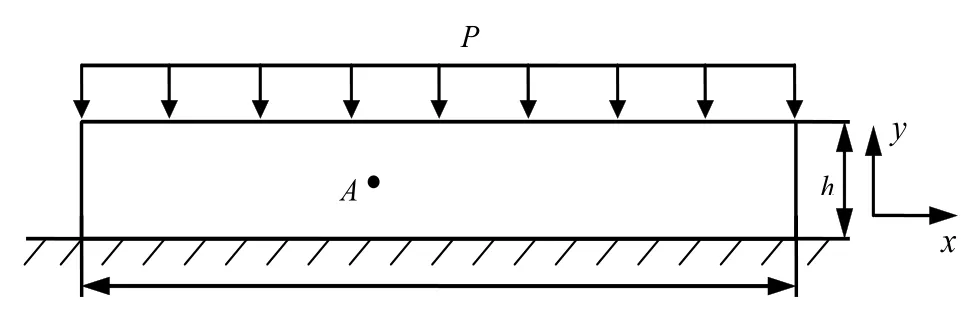
图2 受均匀压力的狭长板

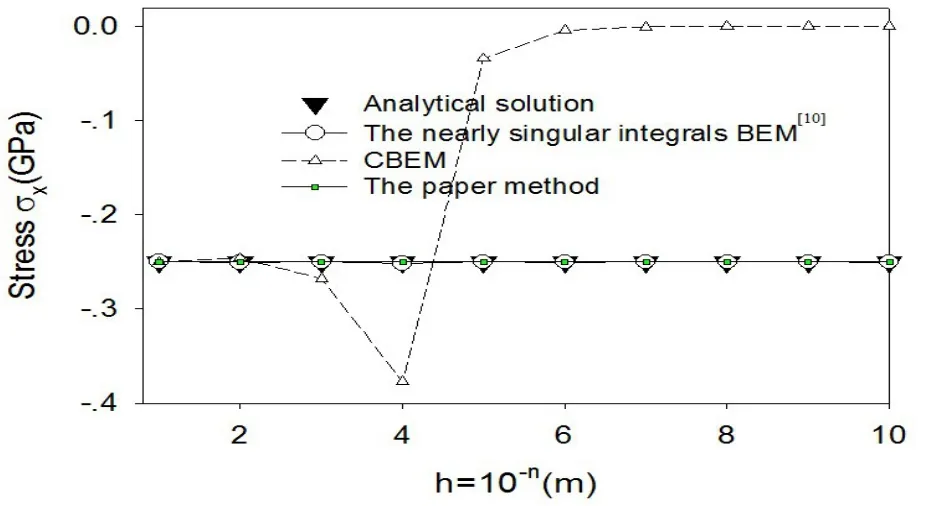
图3 A点的应力

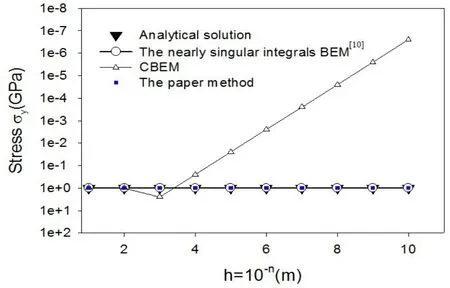
图4 A点的应力σy

图3和4的数据表明，本文所计算的结果即使是在h=10-10m时，依然与精确解非常的吻合。表1、表2的数据表明，本文即使没有进行近奇异积分的处理，但是所计算的结果依然和精确解十分吻合。

3 结论

本文应用边界元法所计算的结果即使没有处理近奇异积分，依然比较精确，究其原因是Mathe⁃matica软件数值精度比较高，其次是智能积分，通常会采用自适应算法计算积分的近似值，对积分区间进行递归分割，直到达到指定的准确度为止。以往近奇异积分的处理即坐标变换是为了将变化比较剧烈的曲线变得比较平缓，这样用Gauss积分法计算近奇异积分式子才能达到很高的精度。由此可见，计算近奇异积分，对于高级的程序语言来说，其智能的积分计算功能已经完全能够胜任近奇异积分计算这项工作，不需要再做任何的处理。

表1 直线x=1.8上内点应力σx的计算结果(h =10-9m)