Perturbative Treatment for Stationary State of Local Master Equation∗
2018-07-09JianYingDu杜建迎andFuLinZhang张福林
Jian-Ying Du(杜建迎)and Fu-Lin Zhang(张福林)
Department of Physics,School of Science,Tianjin University,Tianjin 300072,China
1 Introduction
It is generally impossible to isolate a quantum system from its surroundings,which is referred to an open quantum system.Studying open quantum systems has both theoretical and practical significance,such as in quantum thermodynamics[1−2]and quantum information.[3]However,only few system-environment models can be solved exactly.For most cases,the effects of environment are treated by employing various effective models,e.g.,time dependent Hamiltonian,quantum Langevin and stochastic Schrödinger equations,quantum state diffusion models or Hilbert-space averaging methods.[4−9]
The most widely applied approach is the quantum master equation,[7−9]which can be derived from a quantum system-environment model by the partial trace over the environment under appropriate approximations.The most common approximations are the Born-Markov(factorization and memoryless)approximations and the rotating wave approximations,which lead to the Gorini-Kossakowski-Lindblad-Sudarshan(GKLS)quantum master equation.[10−11]
The local approach is an approximation often invoked in building the quantum master equation of a composite open system with a weak internal coupling,whose subsystems coupled to local environments.The internal coupling is supposed to have no effect on the local dynamical generator,often in the GKLS form,of each individual component.And the master equation is constructed by simply adding the local dynamical generators.The other extreme is the global approach,in which the system with a strong internal coupling is considered as a whole,and the global dynamical generators are derived in the standard procedure to build the quantum master equation.Each of the two approaches has its own pros and cons.The local GKLS master equation is found to be thermodynamic inconsistent,which may lead to a heat current flowing against the temperature gradient.[12]But,in deriving the global one,the eigenvalue problem for the system Hamiltonian can be difficult.In addition,for a global GKLS master equation,the steady-state,which is a mixture of eigenstates of the whole system,is often far from direct product states of subsystems.This makes it to be hard to define the local temperature of a subsystem.[13]Currently,efforts are being made to study the local and global GKLS master equations and test their validity or divergence.[14−21]
In this contribution,we are going to present a perturbative method to solve the stationary states of local master equations,with linear local dynamical generators.The steady-state is,in general,the most important solution of a master equation,e.g.it can be regarded as the quantum counterpart of classical thermodynamic cycle in the sense of self-contained quantum thermal machines.[18−19,21−30]
On the one hand,the perturbative method further simplifies the task to derive the stationary state,which is represented by a series of the strength of weak internal interaction.And on the other hand,the recurrence relation of the steady-state clearly shows the competition between the internal interaction and the trend back to the local stationary state.Particularly,when the local dynamical generators are in the GKLS form,such competition becomes the one between incoherent operations and the unitary creating quantum coherence.[31−32]This pro-vides a possible perspective to relate the thermodynamic consistency with quantum coherence.As two examples,we study the two-qubit model analysed in Refs.[12,14–15]and the three-qubit absorption refrigerator[22,24]to demonstrate our perturbative method and discuss the relation between quantum coherence and thermodynamic consistency.
2 Perturbative Method
In the local approach,the master equation for an open system reads
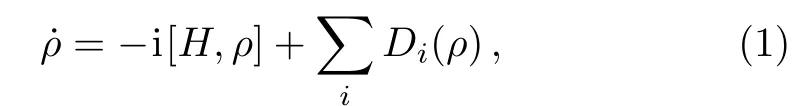
where H is the total Hamiltonian of the whole system,and Diis the local dynamical generator on i-th subsystem induced by the coupling with its environment.The Hamiltonian can be written as the sum of free Hamiltonian of subsystems and internal interaction as
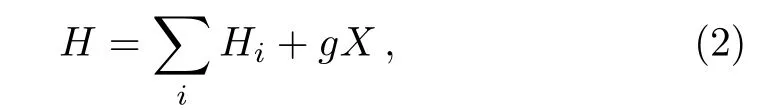
where we denote the interaction Hint=gX with g being a small dimensionless constant and X is a nonlocal operator specifying the couplings.
We assume that the steady-state solution of master equation(1)exists and is unique,satisfying
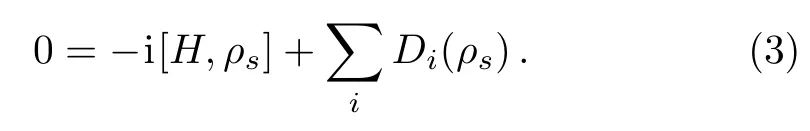
When internal interaction g=0,the solution is simply the direct product of local steady states
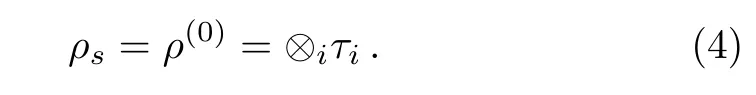
Here the local state τiof a subsystem is determined by
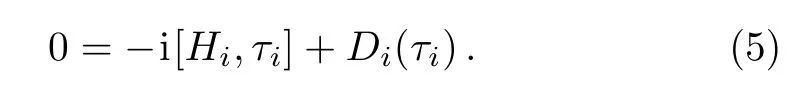
Similar with the perturbation theory described in every textbook on quantum mechanics,we represent the steady state by the series

The zeroth-order term ρ(0)is given by Eq.(4),and the normalization condition requires Trρ(k)=0 for k>0.When the local dynamical generators Diare linear,one can insert the series into Eq.(3)and obtain the recurrence relation
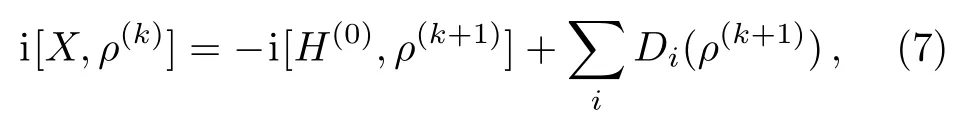
where H(0)=∑iHiis the free Hamiltonian and k=0,1,2,...The steady-state problem described by Eq.(5)is often trivial,e.g.τibeing a thermal state in the temperature of its bath in an equilibrium state.Then,the task becomes to derive ρ(k+1)from the commutator[X,ρ(k)]and the properties of H(0)and Di,starting with ρ(0).
When Diare in the GKLS form,the local steady states τiare functions of free Hamiltonian Hiand thus are incoherent states with respect to the representation of Hi.And,both the two terms in the right hand of Eq.(7)correspond to the changes of ρ(k+1)under incoherent operations in an infinitesimal interval of time,in which the commutator originates from the unitary generated by H0and Difrom the transition and dephasing caused by baths.Whereas,the unitary deriving by the interaction Hintmay produce coherence,when it does not commute with the diagnalized states it acting on.In such case,the recurrence relation(7)shows the fact that,the coherence generated from ρ(k)by the internal interaction is counteracted by the decoherence of ρ(k+1).Hence,the steady-state solution is the result of competition between the internal interaction and incoherent operations.
One can simply rewrap the density matrix ρsto a vector,and simultaneously Diand −to matrices operating on it,as the treatments of stationary state in Ref.[18]and transient state in Ref.[29].In this way,the series ρ(k)can be derived by using the perturbation theory for algebraic eigenvalue problem.[33]In present work,we omit this standard method,but show a process for construction of the series of steady state by using two simple examples in the following parts.In these examples,the generating and destroying of coherence in Eq.(7)are shown visually.
3 Two-Qubit Heat Transfer Network
The first example is the simplest heat transfer network model composed of two qubits,1 and 2,each of which is coupled to a single heat bath with temperature T1andLet us denote the Pauli operators for qubit i asand=(±)/2.The free Hamiltonian is given by

And the two subsystems are weakly coupled to each other with the bipartite operator
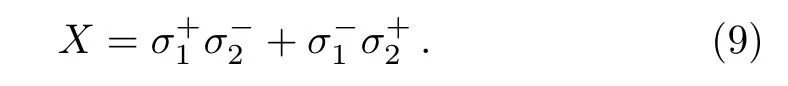
The local steady state τiis a thermal state,

where si=tanh(−βiEi/2)with βi=1/Ti.For simplify,we model the local dissipator for each bath on its corresponding qubit as[22]

where piis the dissipation rate,depending on how well each qubit is relative to its bath.It is a modified version of the one derived from the Jaynes-Cummings(JC)model with the dephasing rate being doubled,[34]and can be rewritten explicitly in the GKLS form(pointed out in the supplementary material of Ref.[22]).
Substituting the zero-order steady state ρ(0)= τ1⊗ τ2and the interaction operator into Eq.(7),one can obtain

where∆s=(s1−s2)/2 and
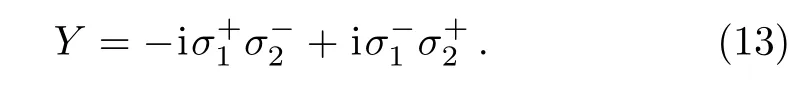
It is obvious that the infinitesimal interaction generates the coherence term Y. One can directly assume the first order ρ(1)consists of Y,which is suppressed by Di.In addition,the commutators[H(0),Y]∝ ∆EX and[H(0),X]∝∆EY,where∆E=E1−E2.That is,the free Hamiltonian rotates the o ff-diagonal term in the space of{X,Y}when ∆E0.Therefore,one can assume
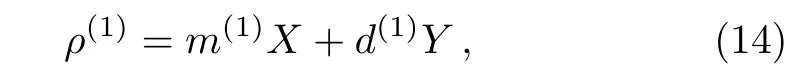
where m(1)and d(1)are the parameters to be determined.Inserting the form of ρ(1)into the right hand of Eq.(7),we obtain

where q=
Substituting the first-order term ρ(1)into the left hand of Eq.(7),the commutators[X,ρ(1)]∝−.It commutes with the free Hamiltonian H0.According with the effects of local dissipators on,we suppose
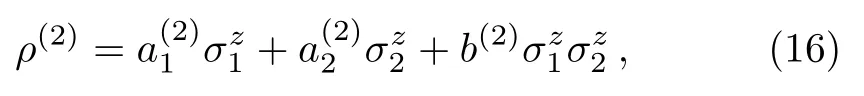
withand b(2)to derive.It is easily to obtain
by using the relation in Eq.(7).The left hand of Eq.(7)for k=2 is given by
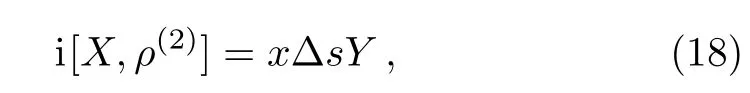
where x= −2q2/[(q2+∆E2)p1p2].The linearity of the right hand leads to
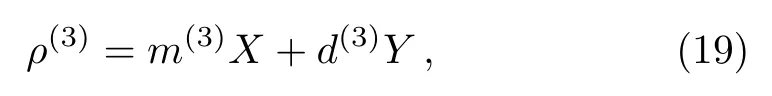
and m(3)=xm(1),d(3)= xd(1),or in other words
From the two steps to derive ρ(2)and ρ(3)and the linearity of the recurrence relation,one can find that the series of ρ(k)for k>0 is composed of two geometric series.That is,the steady state is given by
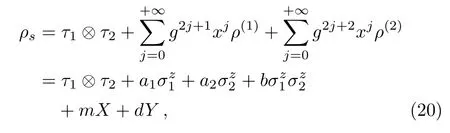
where the parameters can be directly obtained by using the sum formulae of geometric series as
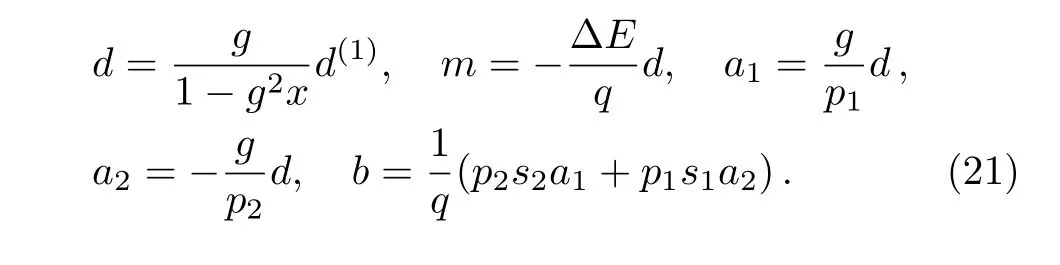
4 Three-Qubit Absorption Refrigerator
We take the three-qubit model of quantum absorption refrigerator as the second example.It is proposed in the study of the fundamental limitation on the size of thermal machines,[22]and has raised a subsequent stream of works about self-contained quantum thermal machines,[18−19,21,23−30]Similar with the two-qubit model studied above,the three qubits 1,2,and 3,interact with three baths,1,2,and 3,at temperatures T1 which extracts heat from the target,and dissipates it into bath 2 through the spiral,qubit 2.The qubit 3 plays the role of the engine,which gains free energy from the hot bath 3,to drive the heat current from the target to spiral. The commutator of the tripartite interation and the zero-order term of steady state= τ1⊗τ2⊗τ3is proportional to the tripartite coherent term Yr=−.Such term is suppressed byby H0=H1+H2+H3to in the space of{Xr,Yr}.We derived the first order of steady state as Here∆Er=E1+E3−E2,qr=q1+q2+q3and∆sr=(s1−s2+s3−s1s2s3)/4.Denoting ri=(1+si)/2Using the similar steps as the case of two-qubit model,the steady state of the three-qubit absorption refrigerator can be represented by the sum of two geometric series.By using the sum formulae of infinite geometric series,one obtains When ∆Er=0,the stateis consistent with the result in Ref.[24]. The steady-state solutions enable us to derive the heat currents and verify the consistency of the local master equation with thermodynamics.The first law of thermodynamics is a conservation law of energy,which can be expressed by the steady-state heat currents Qias[35] The second law for an isolated system is given by[36] stating that the rate of entropy production is nonnegative. The heat current Qiprovided by bath i is defined as which is the change of energy of an open system in state ρ under the influence of Di.It is easy to prove that the sum of all heat currents at steady state is zero,by calculating average energy of the right hand of Eq.(3).That is,the first law of thermodynamics in Eq.(28)is fulfilled.However,the second law may be violated in the cases of nonresonant,i.e. ∆E0 for the two-qubit model and∆Er0 for the refrigerator. The currents of the two-qubit steady state(20)are When the parameter pi= γi[1+exp(−βiEi)],this is formally consistent with the results in Ref.[12],and pi=Ji[1+exp(βiEi)]leads to the ones in Ref.[14].The minor difference between our results and the two mentioned references stems from different dephasing rate.Substituting the currents(31)into the rate of entropy production in(29),one obtains where ξ is a function of all the parameters of the twoqubit model,which is always positive.When∆E=0,it is easy to find that,the two factors in the two square brackets of Eq.(32)are of the same sign,and consequently dS/dt≥ 0.However,when ∆E0,the two factors may have opposite signs,and thus dS/dt<0.For instance,in the case of∆E<0 and∑i(−1)iβiEi>0,the sum of the two may be less than zero.These analyses also apply to the three-qubit refrigerator in steady state(25),since its currents and entropy production are also in the forms as(31)and(32),with the replacing∆E→∆Er,q→qr,d → drand ξ→ ξr>0.These results demonstrate that,the local approach is valid only under the resonance between subsystems. Such inconsistency can be understood by comparing the heat currents(31)with the ones drawn by the internal interaction from subsystems. The later are defined as the influences of the interaction on local energies,=iTr{Hi[Hint,ρ]}.For the two-qubit model in steady state(20),it is easy to obtained that The results for the refrigerator have the same form,with the mentioned replacing d→dr.It is directly to check that,these currents fulfill the second law in Eq.(29)but break down the first law in Eq.(28).Their differences with the heat currents provided by the baths(31)are proportional to the amounts of detuning,and is caused by the energy allocated to global coherent terms of the steady state.Only when the differences vanish,the first and second laws of thermodynamics are fulfilled simultaneously.These analyses do not rely on the compact forms of steady states in Eqs.(20)and(25),as the conflict can be found by using only the first and second orders of the steady states.These results indicate an implicit assumption of the local master equation that,the global terms of a steady state are without influence upon the currents.That is,the local approach requires that no global coherence contributing to total energy is produced in the competition between the internal interaction and couplings with baths.This is similar to the well known fact that,the laws of thermodynamics are broken down when open systems are correlated with their environments.[37−38]Furthermore,we argue that,for a subsystem in the local approach,the rest of a composite open system plays the role of environments.And,the requirement of resonance is similar with the fact that,only the resonant frequencies of reservoirs are involved in the standard GKLS master equation. We present a perturbative method to solve the stationary states of linear local master equations,with the internal interaction being weak enough.This method is demonstrated by the two-qubit heat transfer network and three-qubit absorption refrigerator,in which each qubit and its bath is modeled by a simple reset model as the treatment in Ref.[22].The recurrence relation shows that the stationary state is the result of competition between incoherent operations and the unitary creating quantum coherence.Our two examples indicate that,it is required that no global coherence contributing to total energy is produced in the competition,by the thermodynamic consistency of local master equations. In our investigation of the consistent of local master equations with thermodynamics,we did not compare the results with the open systems under other treatments as in the recent works,[14−21]but analyze consistency of the theory by studying the heat currents drawn by the interaction and the ones provided by the baths.Here,we argue that,the treatment in Ref.[15]is not reasonable to consider a local master equation as the limit of the global one,as they are two different extremes of the internal interactions.It would be interesting to extend our perturbative method to the case with strong system-environment couplings,where the higher-order and non-Markovian effects[39]must be taken into account. [1]G.Gemma,M.Michel,and G.Mahler,Quantum Thermodynamics,Springer,Berlin(2004). [2]J.Gemmer,M.Michel,and G.Mahler,Quantum Thermodynamics:Emergence of Thermodynamic Behavior Within Composite Quantum Systems,volume 784 of Lecture Notes in Physics,Springer Verlag,Heidelberg(2009). [3]M.A.Nielsen and I.L.Chuang,Quantum Computation and Quantum Information,Cambridge University Press,Cambridge(2000). [4]M.V.Berry,Proc.R.Soc.London,Ser.A 392(1984)45. [5]N.Gisin and I.C.Percival,J.Phys.A:Math.Gen.25(1992)5677. [6]J.Gemmer and M.Michel,Eur.Phys.J.B 53(2006)517. [7]H.P.Breuer and F.Petruccione,The Theory of Open Quantum Systems,Oxford University Press,Oxford(2002). [8]C.Gardiner and P.Zoller,Quantum Noise:A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics,Vol.56,Springer Science&Business Media(2004). [9]I.de Vega and D.Alonso,Rev.Mod.Phys.89(2017)015001. [10]G.Lindblad,Commun.Math.Phys.48(1976)119. [11]V.Gorini,A.Kossakowski,and E.C.G.Sudarshan,J.Math.Phys.17(1976)821. [12]A.Levy and R.Koslo ff,Europhys.Lett.107(2014)20004. [13]M.Kliesch,C.Gogolin,M.J.Kastoryano,et al.,Phys.Rev.X 4(2014)031019. [14]P.D.Manrique,F.Rodríguez,L.Quiroga,and N.F.Johnson,Adv.Cond.Matt.Phys.2015(2015)615727. [15]A.Trushechkin and I.Volovich,Europhys.Lett.113(2016)30005. [16]P.P.Hofer,M.Perarnau-Llobet,L.D.M.Miranda,et al.,New J.Phys.19(2017)123037. [17]J.O.González,L.A.Correa,G.Nocerino,et al.,Open Syst.Inf.Dyn.24(2017)1740010. [18]C.S.Yu and Q.Y.Zhu,Phys.Rev.E 90(2014)052142. [19]L.A.Correa,J.P.Palao,G.Adesso,and D.Alonso,Phys.Rev.E 87(2013)042131. [20]G.De¸cordi and A.Vidiella-Barranco,Opt.Commun.387(2017)366. [21]Z.X.Man and Y.J.Xia,Phys.Rev.E 96(2017)012122. [22]N.Linden,S.Popescu,and P.Skrzypczyk,Phys.Rev.Lett.105(2010)130401. [23]A.Levy and R.Koslo ff,Phys.Rev.Lett.108(2012)070604. [24]P.Skrzypczyk,N.Brunner,N.Linden,and S.Popescu,J.Phys.A:Math.Theor.44(2011)492002. [25]N.Brunner,N.Linden,S.Popescu,and P.Skrzypczyk,Phys.Rev.E 85(2012)051117. [26]N.Brunner,M.Huber,N.Linden,et al.,Phys.Rev.E 89(2014)032115. [27]L.A.Correa,J.P.Palao,D.Alonso,and G.Adesso,Sci.Rep.4(2014)03949. [28]R.Kosloff and A.Levy,Annu.Rev.Phys.Chem.65(2014)365. [29]J.B.Brask and N.Brunner,Phys.Rev.E 92(2015)062101. [30]J.Goold,M.Huber,A.Riera,et al.,J.Phys.A:Math.Theor.49(2016)143001. [31]T.Baumgratz,M.Cramer,and M.Plenio,Phys.Rev.Lett.113(2014)140401. [32]M.L.Hu,X.Hu,Y.Peng,et al.,arXiv:quantph/1703.01852(2017). [33]J.H.Wilkinson,The Algebraic Eigenvalue Problem,Clarendon Press,Oxford(1965). [34]J.Y.Du and F.L.Zhang,New J.Phys.20(2018)063005. [35]R.Alicki,J.Phys.A:Math.Gen.12(1979)L103. [36]R.Koslo ff,Entropy 15(2013)2100. [37]D.Jennings and T.Rudolph,Phys.Rev.E 81(2010)061130. [38]M.N.Bera,A.Riera,M.Lewenstein,and A.Winter,Nat.Commun.8(2017)2180. [39]X.Zhao,J.Jing,B.Corn,and T.Yu,Phys.Rev.A 84(2011)032101.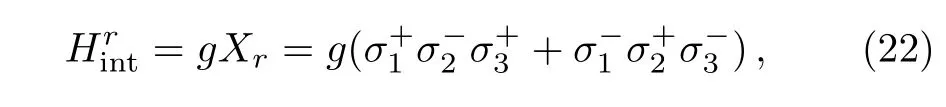
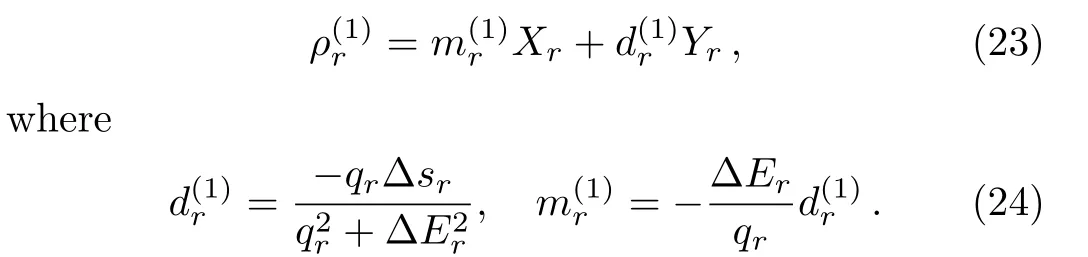


5 Thermodynamic Consistency


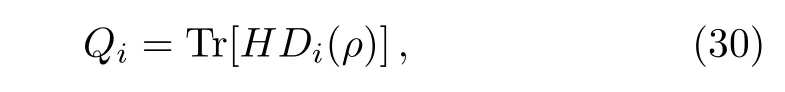
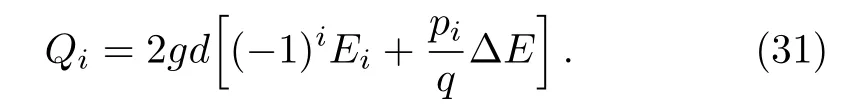
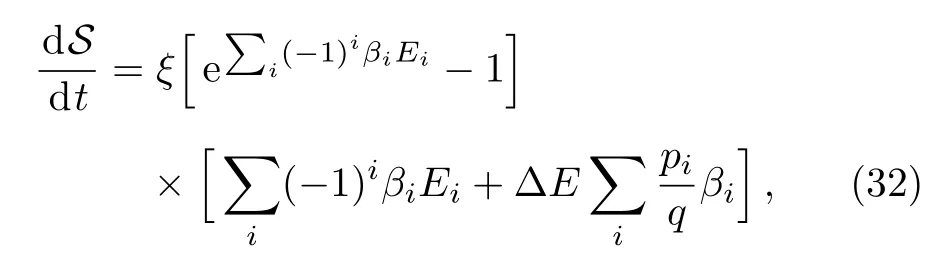

6 Summary
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Electron Correlations,Spin-Orbit Coupling,and Antiferromagnetic Anisotropy in Layered Perovskite Iridates Sr2IrO4∗
- The Three-Pion Decays of the a1(1260)∗
- A New Calculation of Rotational Bands in Alpha-Cluster Nuclei
- Upshot of Chemical Species and Nonlinear Thermal Radiation on Oldroyd-B Nano fluid Flow Past a Bi-directional Stretched Surface with Heat Generation/Absorption in a Porous Media∗
- Detection of Magnetic Field Gradient and Single Spin Using Optically Levitated Nano-Particle in Vacuum∗
- Transverse Transport of Polymeric Nano fluid under Pure Internal Heating:Keller Box Algorithm
