二型模糊真值代数性质
2018-07-04刘志强谭武霜熊清泉
刘志强, 谭武霜, 熊清泉
(四川师范大学 数学与软件科学学院, 四川 成都 610066)

本文在文献[16]的基础上首先讨论了单调函数在连续t-模(┬)与t-余模(┴)上模糊真值运算的性质.然后探讨了连续t-模(┬)与t-余模(┴)上模糊真值运算的性质.紧接着讨论了在最小t-模与最大t-余模下凸模糊集有限并与交的性质.最后讨论了具有相同最大值的凸模糊集的模糊真值代数性质,并且证明了所有具有相同最大值的凸模糊集在二型模糊的并与交运算下构成一个格.
1 预备知识
为了讨论方便,下面给出一些定义和基本结论.设I表示一个单位区间或一个结合代数([0,1],∨,∧,′,0,1),J表示一个有界线性序集或一个结合代数(J,∨,∧,′,0,1).函数┬:I×I→I(┴:I×I→I)是I上的一个t-模(t-余模),满足:
1) 交换律:x┬y=y┬x;
2) 结合律:(x┬y)┬z=x┬(y┬z);
3) 单调性:x≤u且y≤v有x┬y≤u┬v;
4) 边界条件:x┬1=x(x┴0=x).
逐点定义┴-并和┬-交形式如下:
(f∪┴g)(x)=f(x)┴g(x),
(f∩┬g)(x)=f(x)┬g(x).
本文假设┴和┬在I上都是连续的.
定义1.1[2]设S为一个集合,S的二型模糊子集A是一个映射
A:S→Map(J,I).
用Map(S,Map(J,I))表示集合S中的所有二型模糊子集.
定义1.2[2]设f1,f2∈Map(J,I),∀a,u,v,w∈J,运算、定义如下:
1) (f1f2)(a)={f1(u)∧f2(w)|u∨w=a};


4)

集合Map(J,I)在运算、下构成一个代数(Map(J,I),,,其为模糊真值代数.在不混淆的情况下,以下用M表示.
定义1.3[2]设f∈M,fL和fR满足
注1.1函数fL单增,fR单减.用fL和fR分别表示f的L与R运算,显然supf=fRL且fL,fR∈M.
引理1.1设f∈M且f为凸模糊集,记U={u∈J|f(u)=fRL},∀u1∈U,则
(1)
证明当a≥u1时,fL(a)=supf(a)=fLR(a);当a 图1表示了凸函数f的fL与fR的图像. (a) fL (b) fR 定义1.4[2]设f1,f2∈M,则 f1 (2) (3) 定义1.5[16-17]设f1,f2∈Map(J,I),*为J上的一个二元运算,*的┬-扩展运算定义为 ┬f2(w)}. 显然如下结论成立: (4) (5) 引理1.2[2]设f1,f2∈M,则: 5)f1f1=f1,f1f1=f1; 6)f1f2=f2f1,f1f2=f2f1; 引理1.3[16]设f1,f2∈Map(J,I),则: 其中f⊆g⟺(∀u∈J)(f(u)≤g(u)).由于部分文献使用符号不一致,为了不引起混淆,以下统一用⊆表示≤. 引理1.4[16]设f1,f2∈Map(J,I),则: 引理1.5[2]设f1,f2∈Map(J,I),则: (f1 (f1 引理1.6[16]设f1,f2∈Map(J,I),则: (8) (9) 引理1.7[2]设f∈M,则以下条件等价: 1)f是凸函数; 2)f=fL∧fR; 3)f在某处的函数值可表示为一个增函数在该点的函数值和一个减函数在该点的函数值的交. 假设fi∈M(1≤i≤n).记F+={f∈M|f=fL},F-={f∈M|f=fR},即F+和F-分别表示所有单调不减和单调不增连续模糊真值构成的集合.显然,∀f∈F+,f有右最大值,即fR=fLR;∀f∈F-,f有左最大值,即fL=fLR[14]. 定理2.1设fi∈F+(1≤i≤n),则: 证明在连续t-模┬和┴下, (f1∩┬f2)∩┬f3=f1∩┬(f2∩┬f3), (f1∪┴f2)∪┴f3=f1∪┴(f2∪┴f3), 1) 由引理1.4的1)及引理1.6知 又由引理1.4的1)知 即 2) 由引理1.3的2)得 ⊆ 由引理1.2的2)得 故 3) 与2)的证明类似. 4) 由3)得 由注1.1得 (f1∪┴f2)LR=sup(f1∪┴f2)= 即 定理2.2设fi∈F-(1≤i≤n),则: 证明在连续t-模┬和┴下, (f1∩┬f2)∩┬f3=f1∩┬(f2∩┬f3), (f1∪┴f2)∪┴f3=f1∪┴(f2∪┴f3), 1) 由引理1.4的2)及引理1.6知 根据引理1.4的1)得 即 2) 由引理1.2的2)知 ⊆ 由引理1.3的1)知 故 3) 与2)的证明类似. 4) 由3)得 由注1.1得 (f1∪┴f2)RL=sup(f1∪┴f2)= 即 特别地当┬=∧时有如下的结论成立. 推论2.1设fi∈F+(1≤i≤n),则: 推论2.2设fi∈F-(1≤i≤n),则: 注2.1当┴=∨时,可得引理1.2的3).由推论2.1和2.2知 推论2.1和2.2与引理1.2的4)和引理1.3比较可知,对有限个单调增函数在连续t-模(连续t-余模)和有限个单调减函数在连续t-模(连续t-余模)条件下等号成立. 定理2.3设fi∈M(1≤i≤n),则: 证明1)和2)及3)和4)的证明方法分别一致,这里只证明1)与3). 1) 由引理1.5得 (f1f2)RL=((f1f2)R)L= 由定义1.4得 即(f1在和运算下满足结合律[9],可推知(f1f2…类似可证 3) 由引理1.5得 (f1 由定义1.4得 (f1f2 注2.2由定理2.3的1)和2)知在M中有限个函数并的最大值与有限个函数交的最大值相等,且都等于这有限个函数的最大值取小,即 证明由定义1.4和引理1.7有 (f1 (因为f(a)=fL(a)∧fR(a)). (10) 由引理1.1得 当n=2时, (i) 如果a (f1f2)(a)= (ii) 如果u1≤a (f1f2)(a)= (*) (iii) 如果a≥u2,则 (f1f2)(a)= (fi单调不增,即fi∈F-(i=1,2)) 由(i)、(ii)和(iii)有 (f1f2)(a)= 下面假设个数为n-1时结论成立,即 当个数为n时,由(11)式有 下面对(14)和(15)式进行简化,有以下2种情况: 情况1).如果a (a) 当a (b) 当un-1≤a 所以 综合(a)和(b),当a (17) (18) 由(15)、(17)和(18)式有 由情况1)和2)定理得证. 证明证明方法与定理2.4类似,略去. 2.3模糊真值代数用C表示M中所有凸函数的集合,N表示M中所有标准函数的集合,则C和N关于M的运算分别构成M的子代数,同时也是一个Kleene代数[2].令L=C∩N,即为M中所有标准凸函数构成的集合.文献[2]证明了L为一个分配格,同时构成了De Morgan代数和Kleene代数.本小节讨论具有相同最大值的凸隶属函数的集合C(α),证明了集合C(α)在M的运算关系下是M的一个子代数,并且在和运算下构成一个格. 定义2.1设fi∈M,α∈[0,1],定义 其中Λ为一个指标集.若α=1,则fi为标准凸隶属函数. 证明由(10)式知 fi 由结合律可证 图 2 fi∈C(α)(i=1,2,3,4)的图像 推论2.3设f,g∈C(α),则 f(fg)=f(fg)=f. 证明 f(fg)= (fL∧((fR∧g)∨(f∧gR)))∨ (f∧((fRL∧gL)∨(fL∧gRL)))= (fL∧fR∧g)∨(fL∧f∧gR)∨ (f∧fRL∧gL)∨(f∧fL∧gRL)= (f∧g)∨(f∧gR)∨(f∧gL)∨(f∧gRL)= f∧(g∨gR∨gL∨gRL)=f. 引理2.7[2]设f,g,h∈C(α),则 f(gh)=(fg)h, 引理2.8[2]设f,g,h∈C(α),则 f(gh)=(fg)(fh), 由引理1.2的5)和6)和推论2.3及引理2.7知C(α)为一个格.进一步由引理2.8知,C(α)还是一个分配格. 推论2.4设fi∈C(α)(1≤i≤n),则: 证明1) 由定理2.3的1)和3)知 且 由fi∈C(α),即fi最大值相等,故 类似由定理2.3的2)和4)可证明2). (20) (21) 本文主要讨论了二型模糊集的模糊真值以及二型模糊真值在连续t-模(┬)与t-余模(┴)上的性质,得到了二型模糊集在最小t-模和最大t-余模下并与交运算的最大值性质,凸模糊集有限并与交的运算性质.最后证明了具有相同最大值的凸模糊集在模糊真值代数运算下为一个格.对于凸模糊集在模糊真值运算下形成格的其他性质将在以后讨论. [1] ZADEH L. The conpect of a linguitic variable and its application to approximate reasoning-2[J]. Learning Systems and Intelligent Robots,1975,8(4):199-249. [2] WALKER C, WALKER E. The algebra of fuzzy truth values[J]. Fuzzy Sets and Systems,2005,149(2):309-347. [3] WALKER C, WALKER E. Type-2 operations on finite chains[J]. Fuzzy Sets and Systems,2014,236(1):33-49. [4] HARDING J, WALKER C, WALKER E. On complete sublattices of the algebra of truth values of type-2 fuzzy sets[J]. IEEE International Fuzzy Systems Conference,2007,46:1-5. [5] HARDING J, WALKER C, WALKER E. The variety generated by the truth value algebra of type-2 fuzzy and sets[J]. Fuzzy Sets and Systems,2010,161(5):735-749. [6] HARDING J, WALKER C, WALKER E. The Truth Value Algebra of Type-2 Fuzzy Sets:Order Convolutions of Functions on the Unit Interval[M]. Boca Raton:CRC Press,2016. [7] HARDING J, WALKER C, WALKER E. Lattices of convex normal functions[J]. Fuzzy Sets and Systems,2008,159(9):1061-1071. [8] DUBOIS D, PRADE H. Fuzzy Sets and Systems:Theory and Applications[M]. New York:Academic Press,1980. [9] MIZUMOTO M, TANAKA K. Some properties of fuzzy sets of type-2[J]. Inform Control,1976,31(4):312-340. [10] MIZUMOTO M, TANAKA K. Fuzzy sets of type-2 under algebraic product and algebraic sum[J]. Fuzzy Sets and Systems,1981,5(3):277-290. [11] NIEMINEN J. On the algebraic structure of fuzzy sets of type-2[J]. Kybernetica,1997,13(4):261-273. [12] LIANG Q, MENDEL J. Interval type-2 fuzzy logic systems:theory and design[J]. IEEE Trans Fuzzy Systems,2000,8(5):535-550. [13] LIANG Q, MENDEL J. Interval type-2 fuzzy logic systems[C]//Proceeding of the 2000 IEEE International Conference on Fuzzy Systems. Piscataway:IEEE Service Center,2000:328-333. [14] GERA Z, DOMBIA J. Exact calculations of extended logical operations on fuzzy truth values[J]. Fuzzy Sets and Systems,2008,159(11):1309-1326. [15] GONZALO R, HANI H. Join and meet operations for type-2 fuzzy sets with nonconvex secondary memberships[J]. IEEE Trans Fuzzy Systems,2016,24(4):1000-1008. [16] HU B Q, KWONG C K. On type-2 fuzzy sets and their t-norm operations[J]. Information Sciences,2014,255(10):58-81. [17] HU B Q, WANG C Y. On type-2 fuzzy relations and interval-valued type-2 fuzzy sets[J]. Fuzzy Sets and Systems,2014,236(2):1-32. [18] WANG C Y, HU B Q. On fuzzy-valued operations and fuzzy-valued fuzzy sets[J]. Fuzzy Sets and Systems,2014,268(1):72-92.





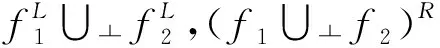

2 主要结论












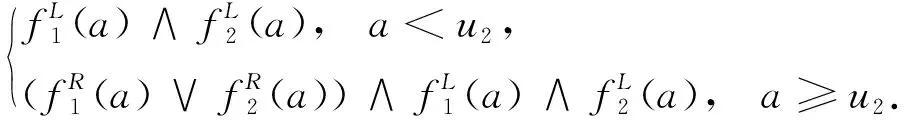







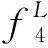






3 结论
