李 扬，许文甫，马双鸽，2

(1.中国人民大学 a.应用统计科学研究中心，b.统计学院，北京 100872；2.耶鲁大学 生物统计系，美国 48097)

一、引 言

大数据时代，数据的高维性与复杂性是对统计研究者的挑战。基于惩罚似然函数的变量选择方法可以在避免遗漏重要影响因素的条件下剔除不重要的变量，使模型更加简洁且易于解释，是近年来统计方法研究的热点[1]。虽然这类方法已被证明有良好的理论与计算性质，但在应用研究中往往受到实际问题与数据的挑战：一方面，虽然成组Lasso等方法可以利用成组惩罚函数刻画影响因素间的相关结构，实现变量的成组选择[2]，但生物信息学的实证研究往往要求分析者在成组变量选择结果上进一步选出具体的影响因素；另一方面，应用研究的数据往往不满足理论模型的分布假设要求。譬如图1中的直方图与正态概率图说明婴儿出生体重不完全服从正态分布假设，存在一定程度的污染(Contamination)。这种污染导致线性回归模型最小二乘估计量的无偏性或有效性受到影响[3]，进而影响基于模型结果对实际问题解释的科学性。

针对第一个问题，分析者可以引入双重惩罚函数同时进行组内变量的选择，如成组Bridge、混合MCP、稀疏成组Lasso等[4-6]。其中成组Bridge具有更好的组选择、变量选择和预测效果[7]。针对第二个问题，当前研究者主要使用具有稳健性的损失函数解决分布异于假设的影响，如复合分位数回归变量选择、最小绝对偏差损失变量选择、指数平方损失变量选择[8-10]。但上述损失函数只能处理来自响应变量异常值的影响，缺乏污染数据的一般性。记观测到的数据A划分为A0和A1两部分，其中A0是满足模型分布假设的部分数据，A1是被污染的部分数据。在污染数据的一般定义中，A1有两个来源：第一种是来自响应变量的均值模型分布污染[11]，第二种是来自随机误差项的异常值污染。均值模型分布污染指A1生成于与A0不同的均值模型，因此两部分数据的方差可能相同但均值存在结构性差异。复合分位数回归等方法只能处理第二种数据污染情况，缺乏对第一种数据污染情况下估计的稳健性。

最小密度势差异准则是Basu等提出的稳健有效参数估计准则，其核心思想是定义经验分布G与假设分布F所对应的密度函数g和f之间的差异，通过最小化该差异得到未知参数的估计[12]。Ghosh和Basu将该估计准则推广到线性回归模型的参数估计[13]。许文甫和林玲构造了基于最小密度势差异准则的变量选择和成组变量选择模型[3，14]。这种稳健变量选择模型既可以处理来自随机误差项的异常值污染，也可以处理来自响应变量的均值模型分布污染，更具有一般性。当数据中不存在污染时，最小密度势差异准则等价于最小二乘估计，具有最小方差的有效性，优于最小绝对偏差损失变量选择等方法[3，15]。

本文以应用研究中存在污染的实际数据为研究对象，探讨稳健的稀疏成组变量选择方法，提出基于最小密度势差异准则的成组Bridge模型。该研究方法既能选择重要的变量组又能在组内选择重要变量。与最小绝对偏差损失等稳健变量选择方法相比，该方法可以同时处理两种污染来源。与成组Bridge等稀疏成组变量选择方法相比，该方法可以在污染数据条件下保持参数估计的稳健性。

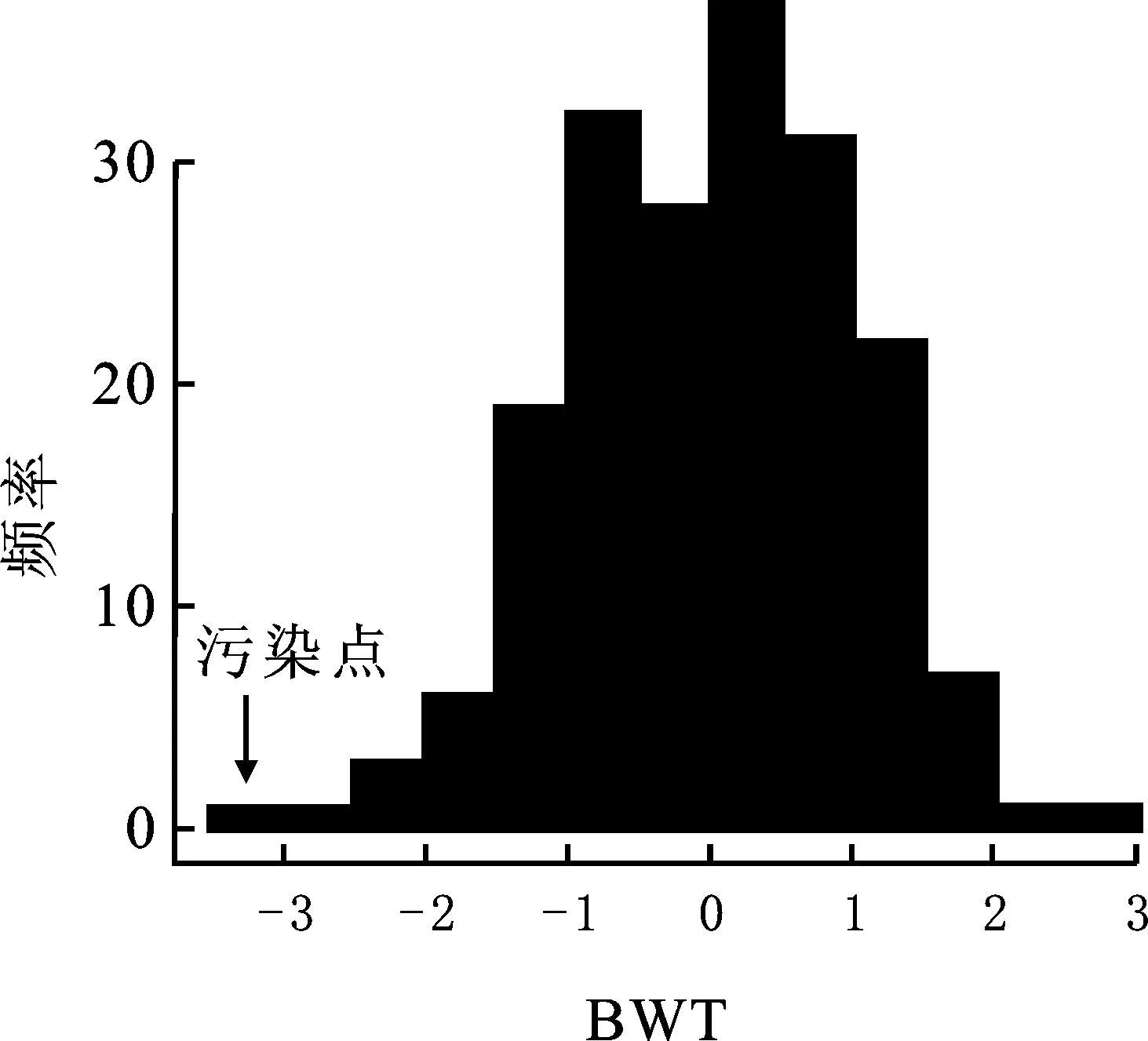
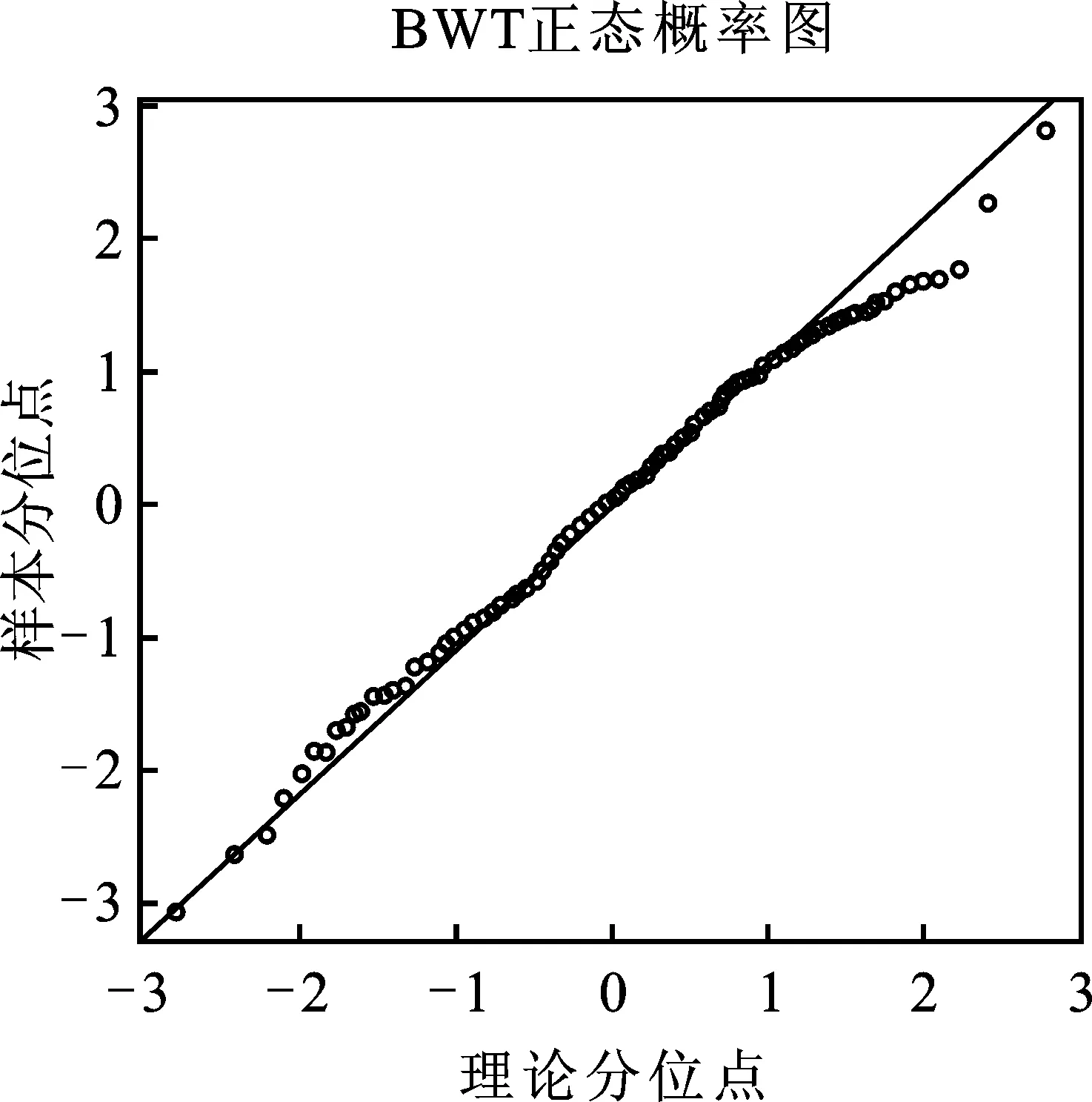
图1 婴儿出生体重(BWT)的直方图和正态概率QQ图

二、基于最小密度势差异准则的成组Bridge模型

(一)目标函数

考虑线性回归模型：

其中，n为样本量，β是p维参数列向量。假定εi独立同分布于N(0,σ2)。借鉴基于罚函数变量选择方法的思想，最小化目标函数(1)式得到基于最小密度势差异准则的成组Bridge估计量。

(1)

(二)参数估计

基于最小密度势差异准则的成组Bridge模型(DPD+gBridge)中包含两类参数：一类是待估参数，如回归系数β及误差项方差σ2；另一类是调节参数，如惩罚调节参数λn和稳健调节参数α。在给定λn和α时，采用迭代方法对β和σ2进行估计。在每一轮迭代循环中，研究者先固定β估计σ2，再固定σ2估计β。当β固定时，目标函数(1)式关于σ2可导，采用牛顿算法对σ2进行估计。当σ2固定时，借鉴Zang等设计β的估计算法：将损失函数关于βj求偏导[16]，得

上式可以看成是加权残差平方和对应的偏导数，权重为：

因此，回归系数β的求解可转化为最小二乘损失成组Bridge估计(OLS+gBridge)的加权求解。加权最小二乘损失成组Bridge估计的计算复杂度等同于普通的Lasso估计[4]。当采用坐标下降算法估计Lasso回归时，每一次迭代的计算复杂度为O(np)。当采用牛顿算法估计σ2，每一次迭代的计算复杂度为O(n2)，所以该算法每一次迭代的整体复杂度为O(n2+np)。当数据量很大时，σ2的估计应该采用其它估计算法，比如二分法，此时每一次迭代整体复杂度为O(log(n)+np)。具体算法如表1。

表1 β及σ2的估计算法

算法中待估参数β和σ2的初始值由不含惩罚约束的最小密度势差异准则估计给出。特别的，算法设计中将DPD+gBridge估计转化为使用指数形式的加权OLS+gBridge估计。若某样本点来自于污染数据部分A1，其残差平方和相对较大，则权重wi相应较小。换言之，DPD+gBridge通过对污染数据施加较小的权重达到估计的稳健性。

针对同一个数据，惩罚调节参数λn越大，惩罚约束的约束越强，DPD+gBridge估计越稀疏；稳健调节参数α越大，污染数据的权重越小，DPD+gBridge估计越稳健。常用的惩罚调节参数选择方法有AIC法、BIC法、交叉验证法。由于AIC准则倾向选择过多的变量，本文考虑基于BIC准则和五折交叉验证的惩罚调节参数选择方法。稳健调节参数的选择既可以与惩罚调节参数使用同样的方法[16]，也可以使用Wang等提出的最小化方差行列式准则法(VAR)[10]。在模拟研究中，本文通过数值模拟分别比较惩罚调节参数与稳健调节参数的最优选择方法。

三、模拟研究

本文通过模拟数据分析完成两个研究目的：一方面，确定调节参数的选择方法；另一方面，考察DPD+gBridge在稀疏性和稳健性的表现。模拟研究中样本量n固定为200，分别比较不同污染数据来源、不同污染比例下DPD+gBridge的表现。根据Zang等讨论的建议，稳健调节参数α的候选集合为{0.01,0.05,0.1,0.2,0.3,0.4,0.5,0.6}[16]。根据污染数据来源的差异，考虑两种情况：

(1)均值模型分布污染。污染数据A1来自与A0不同的均值模型：污染数据A1对应生成模型M1比A0对应生成模型M0多四个重要的自变量，其参数来自均匀分布U(3,5)，两模型其他自变量的参数设定相同。

(2)随机误差分布污染。污染数据A1的误差分布与A0不同，污染数据A1对应生成模型M1的随机误差项来自t(1)分布，A0对应生成模型M0的随机误差项来自正态分布。

(一)仿真设定与评价准则

情形1.1污染数据来自均值模型，组大小相等。

每个变量组包含8个变量，一共有J=5个组，p=40个变量。前两组为重要变量组，共有13个重要自变量，即：

(β)1,β2,…,β8)=(0.5,0.6,…,1.2)

(β9,β10,…,β13,β14,…,β16)=(1.4,1.4,…,1.4,0,…,0)

(β17,β18,…,β40)=(0,0,…,0)

污染数据A1对应生成模型M1额外多四个重要的自变量，其参数来自均匀分布U(3,5)。

自变量生成如下：

其中，gi表示大于(i-1)/8的最小正数。R1,R2，…,R40独立同分布于标准正态分布。Zgi服从均值为0，方差协方差矩阵为AR(1)的多元正态分布。随机误差项服从均值为0，标准差为2的正态分布。

情形1.2污染数据来自均值模型，组大小不等。

前三个变量组各包含10个变量，后三个变量组各包含4个变量，一共有J=6个组，p=42个变量。其中第一、二、四、五组为重要变量组，共有21个重要自变量，即：

(β1,β2,…,β10)=(0.5,0.6,…,1.4)

(β11,β12,…,β15,β16,…,β20)=(0.5,0.6,…,0.9,0,…,0)

(β21,β22,…,β30)=(0,0，…,0)

(β31，β32，…，β34)=(1,1，…,1)

(β35,β36,β37,β38)=(1.2,1.2,0,0)

(β39,β40,…,β42)=(0,0，…,0)

污染数据A1对应生成模型M1额外多4个重要的自变量，其参数来自均匀分布U(3,5)。

自变量生成如下：

其中，当1≤i≤30时，gi表示小于i/10+1的最大正数；当31≤i≤42时，gi表示小于(j-30)/4+1的最大正数。R1,R2…，R42独立同分布于标准正态分布。Zgi服从均值为0，方差协方差矩阵为AR(1)的多元正态分布。随机误差项服从均值为0，标准差为2的正态分布。

情形2.1污染数据来自随机误差分布，组大小相等。

自变量与回归系数设定同情形1.1。污染数据对应的随机误差项服从自由度为1的t分布，非污染数据对应的随机误差项服从均值为0方差为2的正态分布。

情形2.2污染数据来自随机误差分布，组大小不等。

自变量与回归系数设定同情形1.2。污染数据对应的随机误差项服从自由度为1的t分布，非污染点对应的随机误差项服从均值为0方差为2的正态分布。

从变量选择、参数估计及预测精度等角度衡量方法的优劣。

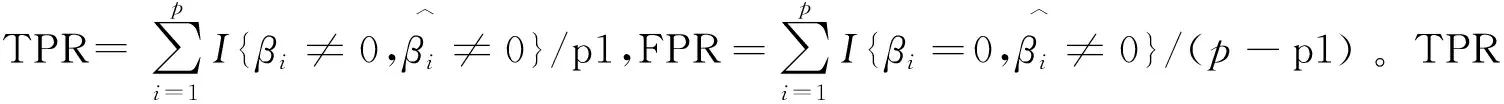
(二)数值结果分析

1.惩罚调节参数λn的选取方法

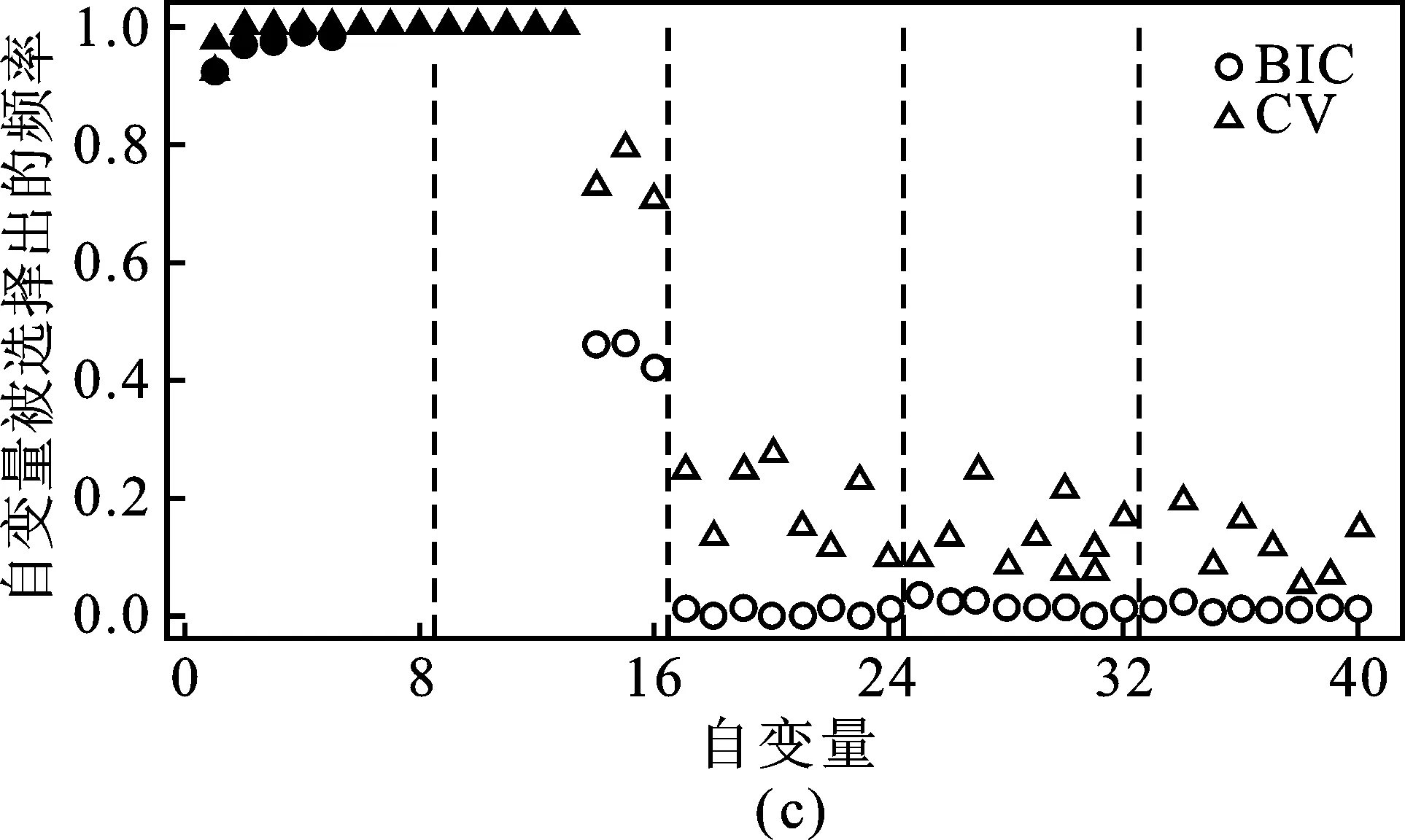
通过数值模拟比较两种惩罚调节参数λn选取方法在基于最小密度势差异准则的成组Bridge模型下的表现。图2是DPD+gBridge在模拟情形1.1下固定稳健调节参数时不同污染数据比例的变量选择频率示意图。其中两条虚线间表示同一组变量，实心代表真模型中重要的变量，空心代表真模型中不重要的变量，圆形代表BIC准则选择的结果，三角代表五折交叉验证法选择的结果。图2表示，当污染数据比例固定时，BIC准则与交叉验证法选择确定的惩罚程度在重要变量的频率相差无几，但交叉验证法确定的惩罚调节参数倾向于选择出更多的不重要变量，导致模型过于复杂。鉴于此，BIC准则更适用于DPD+gBridge中惩罚调节参数的选取。

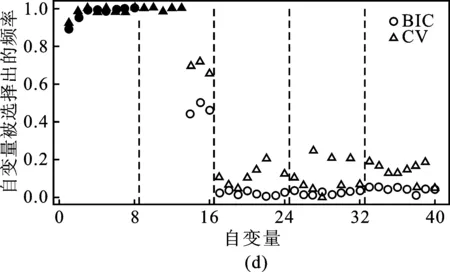
2.稳健调节参数α的选取方法

通过数值模拟比较两种稳健调节参数α选取方法在基于最小密度势差异准则的成组Bridge模型下的表现。图3是DPD+gBridge在模拟情形1.1下固定惩罚调节参数时不同污染数据比例的变量选择频率示意图。其中两条虚线间表示同一组变量，实心代表真模型中重要的变量，空心代表真模型中不重要的变量，圆形代表BIC准则选择的结果，三角代表VAR法选择的结果[10]。图3表示，随着污染数据比例的增加，VAR法确定的稳健调节参数在重要变量的选择和不重要变量的剔除上均优于BIC准则确定的稳健调节参数，选择结果与真实模型更接近。因此，VAR法更适用于DPD+gBridge中稳健调节参数的选取。

另一方面，当使用BIC准则选择最优惩罚调节参数时，模拟情形1.1下不同稳健调节参数选取方法下DPD+gBridge模型的参数估计与预测精度效果如图4。由图4可知，同等条件下，VAR法确定的稳健调节参数下DPD+gBridge在参数估计和预测精度上均优于BIC法则下的结果。鉴于此，建议后续研究中使用BIC法则选取最优的惩罚调节参数λn，使用VAR法选取最优的稳健调节参数α。

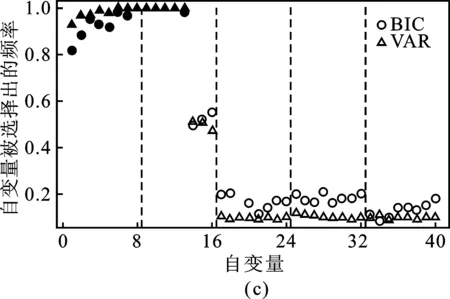
图3 模拟情形1.1，不同稳健参数选取方法下DPD+gBridge变量选择频率示意图

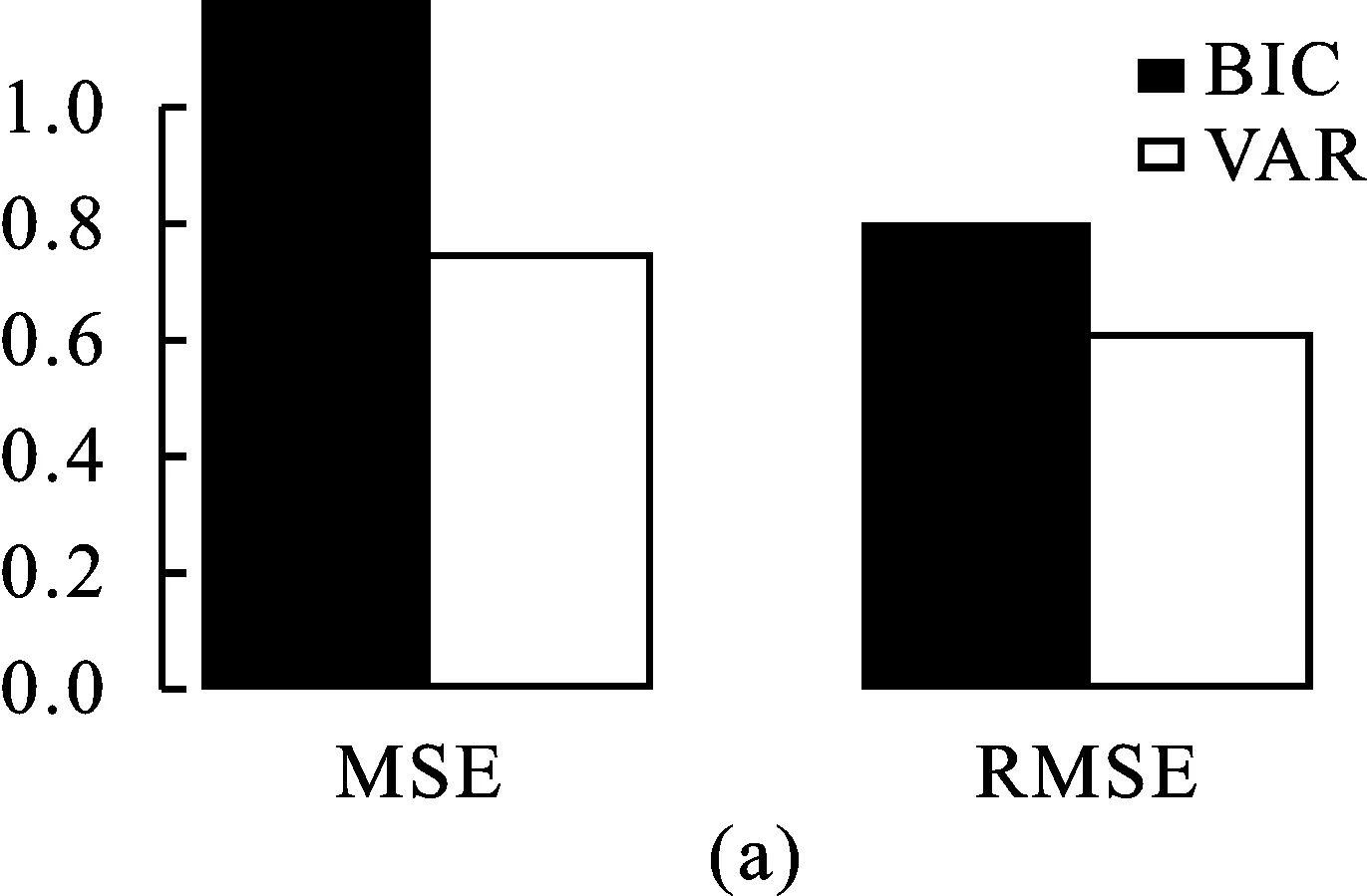
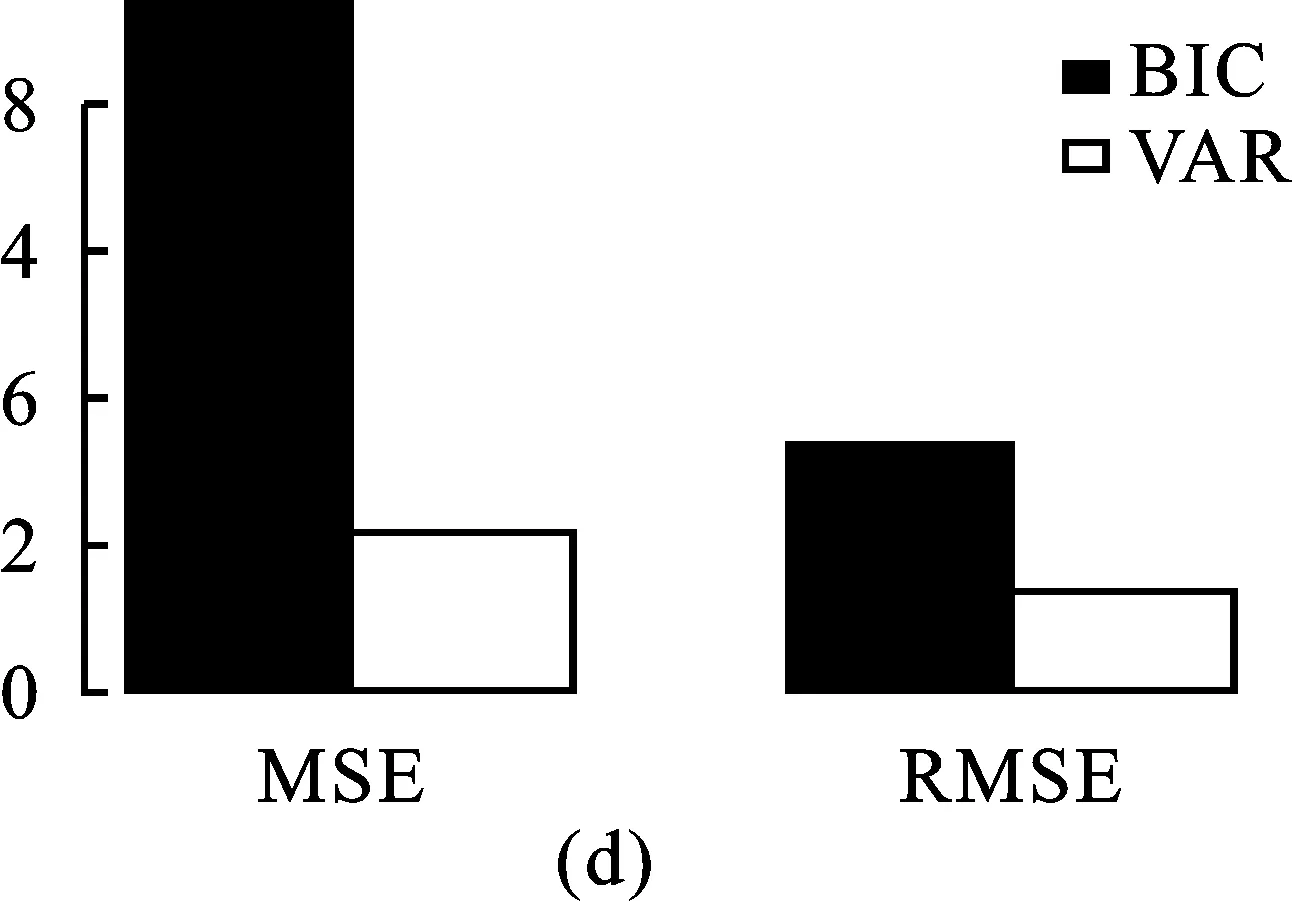
图4 模拟情形1.1，BIC法选取λn，不同稳健参数选取方法下DPD+gBridge估计与预测精度*其他模拟情形下，DPD+gBridge的MSE和RMSE结果类似，不再一一复述。

3.模型结果比较

针对模拟情形1.1至2.2，本文通过数据模拟分析比较不同污染数据比例下OLS+gBridge和DPD+gBridge的表现。通过表2对比可以发现如下结论：

(1)固定污染数据比例时，与OLS+gBridge相比，DPD+gBridge的TPR较大、FPR与FPRG较小，说明后者有较好的组选择和变量选择效果；

(2)固定污染数据比例时，与OLS+gBridge相比，DPD+gBridge的MSE与RMSE较小，说明后者有较好的参数估计与模型预测精度；

(3)随着污染比例的升高，DPD+gBridge的上述优势越明显；

(4)上述现象在不同污染数据来源情形下皆存在，说明DPD+gBridge适用于处理不同来源的污染数据；

(5)上述现象在变量组不同大小时皆存在，说明DPD+gBridge的稳健稀疏成组优势在不同变量组大小下都适用。

综上，当存在污染数据导致实际数据不完全符合模型假定时，基于最小密度势差异准则的成组Bridge模型是适用的稳健稀疏成组变量选择方法。该方法在变量选择、参数估计与模型预测精度上模型优于基于最小二乘损失的传统方法。

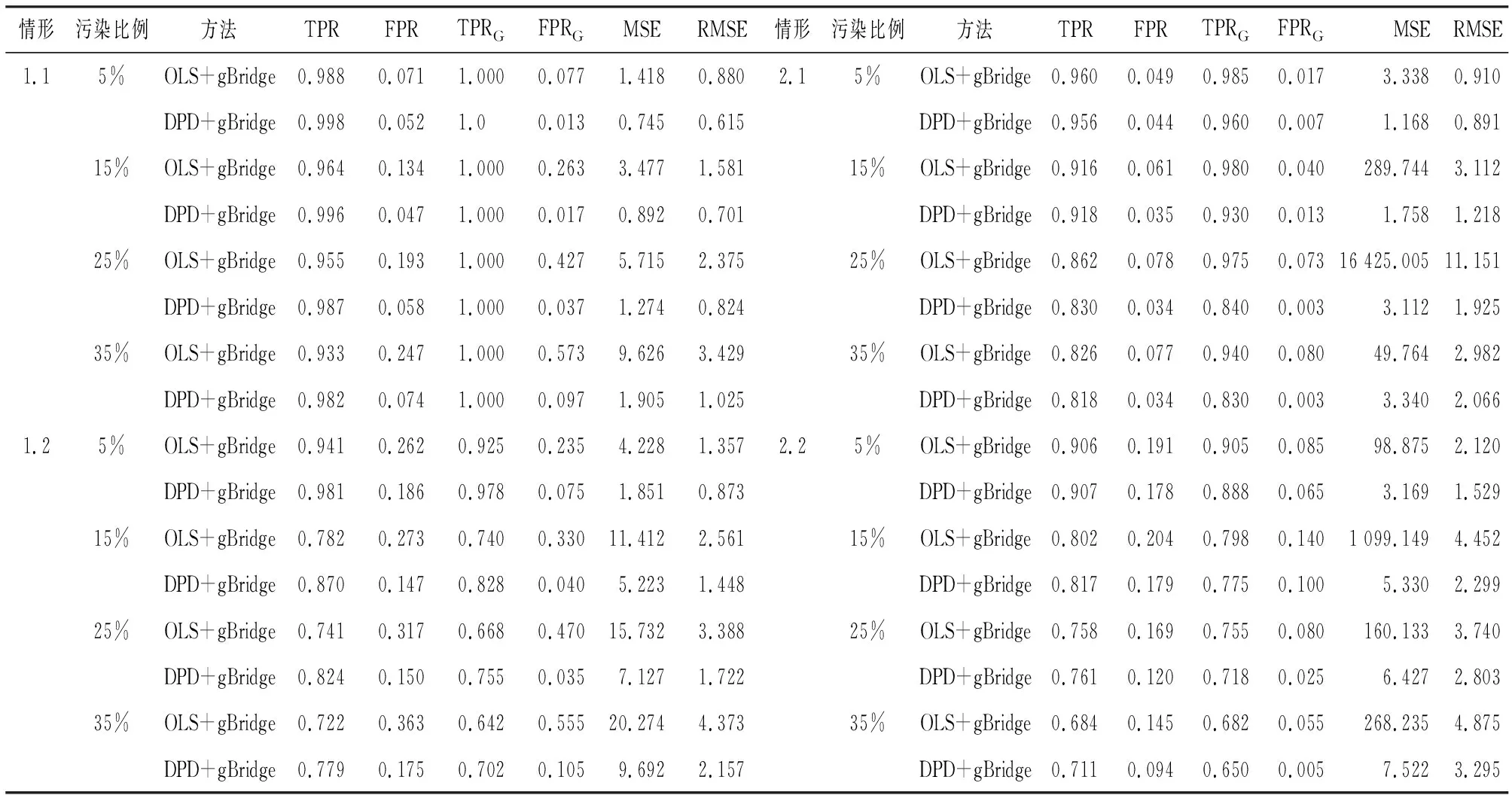
表2 不同情形下的模拟结果

四、实证研究

本文通过对婴儿出生体重数据[17]26的变量选择实证分析讨论稳健稀疏成组变量选择模型在污染数据上的应用效果。该数据集记载了189个婴儿出生体重(BWT)和可能受母亲因素影响的8个变量。8个变量包含2个连续型变量，分别是母亲的年龄和母亲未怀孕前的体重，其余变量为类别数据。图1是响应变量BWT的直方图和QQ图。从直方图可以发现，响应变量中可能存在少量污染点。QQ图说明响应变量不严格服从正态分布，印证了直方图的结论。前期研究发现，母亲的年龄和母亲未怀孕前的体重对婴儿出生体重的影响可能具有三次多项式关系[18]。因此研究者将上述两变量的一次项、二次项和三次项分为两组纳入初始模型，将每个类别型变量对应哑变量作为组纳入初始模型，如表3。

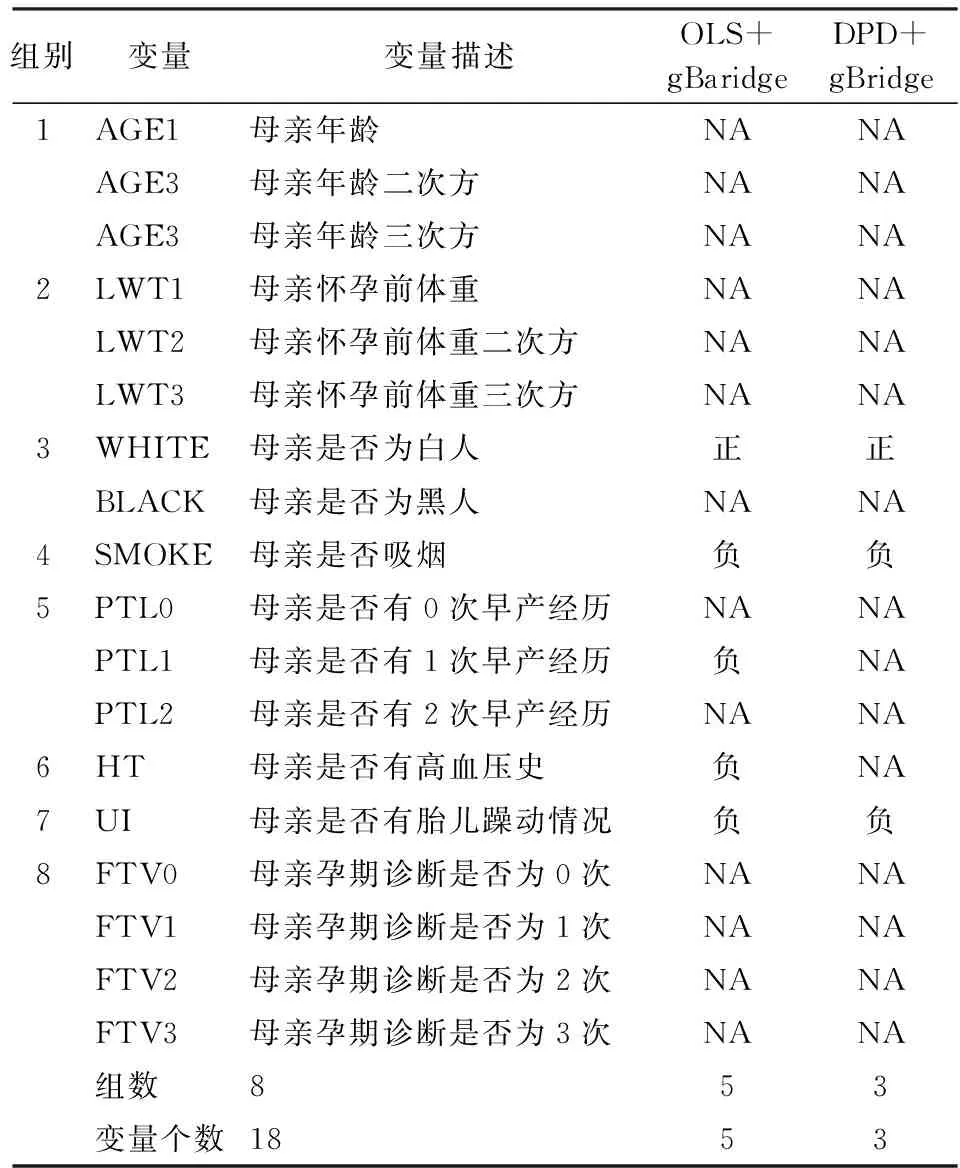
表3 变量说明及选择结果

本文将数据随机划分为训练集(75%)和测试集(25%)，分别拟合OLS+gBridge和DPD+gBridge模型。将上述过程重复100次，比较两种方法在变量选择和预测精度上的表现。图5(a)和图5(b)分别是OLS+gBridge和DPD+gBridge的变量选择频率图，柱子的高度代表该变量在100组模型中被选择出的次数，柱子上方数字代表100组参数估计结果的正负关系一致性：若数字为1，说明当该变量被选择出来时其参数估计结果总是正数；若数字为-1，说明当该变量被选择出来时其参数估计结果总是负数；若数字为0，说明100次建模中该变量都没有被选择出来或者该变量参数估计结果中正负各半。因此，该数值的绝对值越接近1，说明参数估计结果越稳健。图5(b)中所有选择超过半数(50次)的柱子对应数值的绝对值都为1，说明该方法的估计结果十分稳健。相比之下，图5(a)中的结果就显得“摇摆不定”，说明OLS+gBridge在不同数据划分时参数估计结果的变异较大，其原因是不同训练集中不同的污染数据对估计结果产生影响。

由表3中的模型选择结果可知，OLS+gBridge与DPD+gBridge都选择出WHITE(母亲是否为白人)、SMOKE(母亲是否吸烟)和UI(母亲是否有胎儿躁动情况)且估计结果符号一致。OLS+gBridge额外选择出PTL1和HT两个变量。虽然实证研究时真正起作用的变量未知，但由本文模拟研究可知OLS+gBridge倾向多选出并不重要的变量。图5(c)表明DPD+gBridge的中位预测误差低于OLS+gBridge的中位预测误差且误差变异性较小，说明在应用研究中使用本文提出模型能获得更加准确的预测精度且有效性更高。

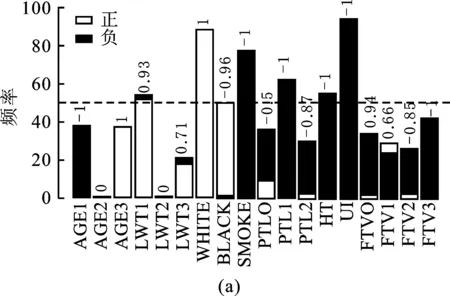
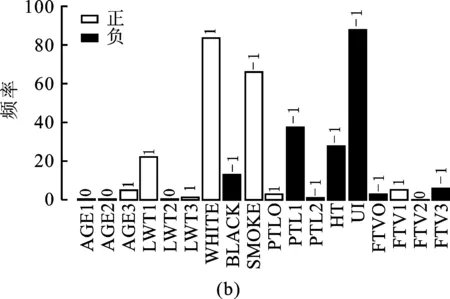
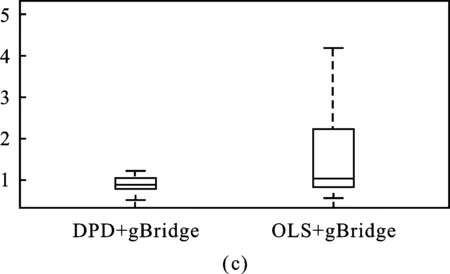
图5 实证数据变量选择频率及预测误差示意图

图5中，(a)为OLS+gBridge变量选择频率图，(b)为DPD+gBridge变量选择频率图，正表示变量对应的回归系数估计值大于0，负表示变量对应的回归系数估计值小于0。(c)为预测结果箱线图。图(a)和(b)中数字表示100次模型结果中该变量回归系数被估计为正值的比例减去被估计为负值的比例。

五、总结与展望

本文针对应用研究中污染数据的成组稀疏变量选择问题，构建了基于最小密度势差异的成组Bridge变量选择模型，设计有效的加权坐标下降算法并通过数值分析讨论了稳健调节参数与惩罚调节参数的选取问题。模拟分析结果表明该方法在不同类型不同比例的污染数据情况下均具有较好的稳健性与稀疏性，完成了拟解决的关键问题。实证数据分析表明该方法在应用研究中具有良好的适用性，变量选择结果稳健且稀疏。特别的，该方法预测误差不仅在平均水平上较小，且具有较小的离散程度。这说明在实证数据中对随机样本使用该方法进行成组稀疏变量选择均可得到具备准确预测能力的精简模型。

在本文研究基础上，有如下两方面可在后续研究中进一步讨论。其一，基于惩罚似然函数的变量选择方法本质上是一种参数估计。由于优化过程带有研究者设定的惩罚约束，其估计量的抽样分布需结合目标函数进行推导，进行选择后的统计推断[19-20]。其二，随着数据采集的便利，大规模数据集越来越多见于各领域的应用研究[21]。大规模数据中难免存在来自其他总体的污染数据，因此本文研究方法可以应对大数据量的挑战。对于大规模数据，分治自助算法是一种可行的并行式算法[22]。当分治自助算法应用到本文提出的算法中，每一次迭代的计算复杂度将会降为O(log(b)+bp)×r，其中b表示分治自助算法中无放回抽样的样本量大小，r表示分治自助算法中通过自助算法抽取的样本量个数。然而，如何针对大规模数据结构设计适宜的分布式并行算法，在保证精度的前提下提高运算效率，是后续研究中值的考虑的问题。

参考文献：

[1] Fan J，Lv J.A Selective Overview of Variable Selection in High Dimensional Feature Space[J].StatisticaSinica，2010(1).

[2] 李扬，赵青，马双鸽.生物统计的研究进展与挑战[J].统计研究，2016，33(6).

[3] 许文甫.基于密度势差异的稳健变量选择方法研究 [D].北京：中国人民大学，2015.

[4] Huang J，Ma S，Xie H，et al.A Group Bridge Approach for Variable Selection [J].Biometrika，2009，96(2).

[5] Zhang C.Nearly Unbiased Variable Selection Under Minimax Concave Penalty [J].The Annals of Statistics，2010，38(2).

[6] Simon N，Friedman J，Hastie T，et al.A Sparse-Group Lasso [J].Journal of Computational and Graphical Statistics，2013(2).

[7] Matsui H.Sparse Regularization For Bi-Level Variable Selection[J].Journal of the Japanese Society of Computational Statistics，2015，28(1).

[8] Zou H，Yuan M.Composite Quantile Regression and the Oracle model selection theory[J].The Annals of Statistics，2008(3).

[9] Wang H，Li G，Jiang G.Robust Regression Shrinkage and Consistent Variable Selection Through the LAD-Lasso[J].Journal of Business & Economic Statistics，2007，25(3).

[10] Wang X，Jiang Y，Huang M，et al.Robust Variable Selection with Exponential Squared Loss[J].Journal of the American Statistical Association，2013，108(502).

[11] Wu C，Ma S.A Selective Review of Robust Variable Selection with Applications in Bioinformatics[J].Briefings in bioinformatics，2014，16(5).

[12] Basu A，Harris I R，Hjort N L.Robust and Efficient Estimation by Minimizing a Density Power Divergence [J].Biometrika，1998，85(3).

[13] Ghosh A，Basu A.Robust Estimation for Independent Non-homogeneous Observations Using Density Power Divergence with Applications to Linear Regression [J].Electronic Journal of Statistics，2013，7(7).

[14] 林玲.基于密度势差异法的稳健群组变量选择方法 [D].北京：中国人民大学，2016.

[15] Leng C.Variable selection and coefficient estimation via regularized rank regression[J].Statistica Sinica，2010,20(1).

[16] Zang Y，Zhao Q，Zhang Q，et al.Inferring Gene Regulatory Relationships with a High-dimensional Robust Approach [J].Genetic Epidemiology，2017(41).

[17] Hosmer D W，Lemeshow S.Applied Logistic Regression [M].New York：John Wi-lley& Sons Inc，1989.

[18] Yuan M，Lin Y.Model Selection and Estimation in Regressionwith Grouped Variables[J].Journal of the Royal Statistical Society，2006，68(1).

[19] Taylor J，Tibshirani R J.Statistical Learning and Selective Inference[J].Proceedings of the National Academy of Sciences，2015，112(25)

[20] Lee J D，Sun D L，Sun Y，et al.Exact Post-selection Inference，with Application to the Lasso[J].The Annals of Statistics，2016，44(3).

[21] 柳向东，李凤.大数据背景下网络借贷的风险评估——以人人贷为例[J].统计与信息论坛2016(5).

[22] Kleiner A，Talwalkar A，Sarkar P，M I Jordan.A Scalable Bootstrap for Massive data [J].Statistical Methodology，2014，76(4).