杨淑丹 董方敏

（三峡大学计算机与信息学院 宜昌 443002）

1 引言

电力系统潮流计算在电力系统规划预测、生产运行、调度管理、科学计算中有着广泛的应用。随着电力网络大规模、强耦合的特点日益突出，传统的串行潮流计算已经无法满足大电网仿真和实时模拟的要求，高效的并行潮流算法正成为研究的热点。从数学角度来看，潮流计算是求解一组由有功、无功功率、电压和功角构成的非线性方程组，求解时间占达整个潮流计算时间的70%以上，因此对潮流并行计算中的方程组求解方法的研究是实现实时仿真计算的关键。

本文针对电力系统潮流并行计算中的方程组求解这一核心问题，分析了潮流并行计算大型矩阵常用算法，通过对稀疏矩阵压缩为稠密矩阵的算法以及矩阵分块算法进行性能比较，给出了不同算法的适用范围；同时，对常用的潮流计算线性方程组求解并行算法进行探讨，对比分析了共轭梯度法、广义极小残差法等不同算法的优点和局限性；并对进一步的研究方向进行了展望。

2 电力系统潮流计算模型

电网稳定状态特性通常采用电力系统潮流计算进行描述。设网络节点数为n，PQ节点数为m-1，PV节点数为n-m，则可以将潮流方程表示成为以下直角坐标形式：

式（1）是第i个电力系统有功功率方程式，共有n-1个，式（2）是第i个无功功率方程式，共有n-m-1个。其中，Pi为PQ和PV节点注入的有功功率，Qi为PV节点注入的无功功率，ei和 fi分别为迭代过程中节点电压的实部、虚部，ej和 fj分别为平衡点电压的实部、虚部，Gij为节点的自导，Bij为节点间的互导。

求解潮流计算的方法有很多，最常用的算法为牛顿拉夫逊法。其修正方程式如下

式中，ΔPi、ΔQi为节点的注入有功功率和无功功率，Δei、Δfi为节点电压不平衡量的实部和虚部，i=1，…，n。修正方程也可简写为

其中，Δf为不平衡量的列向量，J为雅可比矩阵，Δx为节点电压列向量。根据上述公式，可以将电力系统潮流计算转化为对线性方程组的求解问题，即

在大规模电网中，由于节点之间的连接线远少于电力系统，大型系数矩阵 A一般为高度稀疏阵。因此，通常采用不同的大型稀疏阵压缩算法来节省存储空间，以及通过矩阵分块方法提高潮流并行计算效率；同时，可对线性方程组求解算法进行优化，针对不同情况选用合适的并行算法进行求解，提高运行效率。本文将从大型稀疏矩阵处理算法以及方程组并行求解算法两个方面，来探讨分析电力系统潮流并行计算中方程组求解的问题。

3 潮流并行计算矩阵处理算法

3.1 稀疏矩阵压缩为稠密矩阵算法

为了减少存储空间，便于方程组并行求解，通常采用稀疏阵压缩算法改进方程组的求解，下面将依次介绍COO，ELL，HYB三种压缩方法。

1）COO（Coordinate form）存储

COO存储［1～2］是采用三元组对稀疏矩阵的非零元进行存储，其中row，column，value分别代表元素所在的行、列和元素的值，三元组分别用三个数组进行存储。COO存储不存在数据填充的问题，压缩比较彻底，但是缺乏行、列的规整性，因此并行时的性能一般。

2）ELL（ELL-pack form）存储

ELL存储［3］是使用一个n×k的矩阵进行存储，k指非零元素最多行的非零元素数目，ELL存储不适用于行之间非零元相差很大和非零元很少的稀疏矩阵。

3）HYB（Hybrid form）存储

HYB存储［4］是上述两种存储方式的综合，可实现GPU+CPU同时进行运算，来减少运算时间。其实现算法可描述如下：

输入：稀疏矩阵A，稀疏矩阵行数N，列数M，行非零元素的下限值min；

若每行中非零元数目＜min

则非零元存储在ELL格式中，在GPU中运算；

否则

将其存储在COO格式中，在CPU中运算。

但该算法存在任务分配不均、GPU和CPU的访问存储器和调度模式不同、而容易造成时间浪费等问题，通常可从数据分割、数据共享、存储算法等方面进行改进。

表1对上述三种矩阵压缩存储方法进行了对比。

表1 稀疏矩阵压缩为稠密矩阵的算法对比

3.2 矩阵分块算法

采用矩阵分块算法，能够将大型矩阵分割成多个小型矩阵，有利于进行并行运算，减轻运算压力。下面分别介绍对角加边法，单、双对角加边法这三种分块算法：

1）对角加边法矩阵A进行对角加边变换（block bordered diag⁃onal form，BBDF）［5～7］的方式大致可以分为三类：节点撕裂法，支路切割法，统一网络分块法。下面分别介绍这三种分块方法：

（1）节点撕裂法

节点撕裂法［8］是将两个系统中交集部分取一合适节点，进行撕裂，使得两个系统都多一个节点，使得研究的系统简单方便，如图1所示。

图1 节点撕裂法

其中S1和S2为两个区域电网，SA为由边界节点构成的上级电网，S1in和S2in为两个区域电网的内部节点，A为边界节点的集合，A1，A2，A3为同一边界节点在不同区域的分区，节点撕裂后平衡状态方程为

式中，uA1，uA2为两个分裂区域的电压，θ1，θ2为分裂区的相角，PA1，QA1，PA2，QA2分别为两个分裂区的有功和无功功率。

（2）支路切割法

支路切割法［9～10］即在子网络之间的联络线处加入电流源来代替各子网络间的耦合状态，电流源矢量作为该方法的协调变量，如图2～3所示。

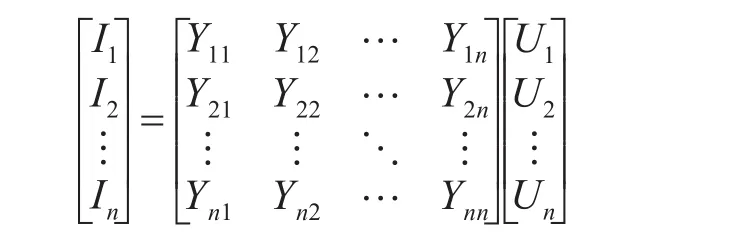
根据推导，最终得到第i个子网络的注入电流的不平衡方程：

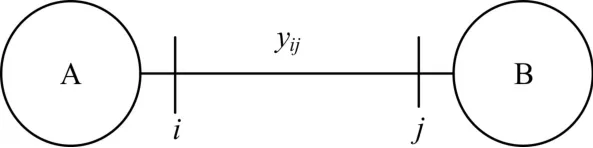
图2 互联电力系统

图3 互联电力系统的分解

（3）统一网络分块法

统一网络分块法是对大规模电力系统进行网络分块，利用节点编号优先顺序的理论来对网络进行划分。通常有静态优化法，半动态优化法，动态优化法三种编号方法［11］，半动态优化法使用最为广泛。下面以五节点网络为例依次介绍这三种编号方法：

图4 有向A图

①静态优化法：按照每个节点出线度由小到大的顺序进行编号，则有向A图编号顺序即为静态优化编号方法。

②半动态优化法：先编号出线度最小的节点，进行消去，其次为消去节点后剩余节点出线度最少的节点进行编号，依次类推…，图中1，2节点编号不用更改，消去这两个节点节点以后，剩余节点的出线度相同，所以可任意编号。

③动态优化法：对节点先不进行编号，对任意节点进行消去，为消去后出现支路最少的节点先编号，依次类推…，图中1，2，3，4节点，由于消去不产生注入元，可任意顺序消去。

对角加边法中三种方法各有特点，表2对这三种方法特点进行比较分析。

2）单、双边块对角法

采用对角加边分块法，能够将大型矩阵分割成多个小块矩阵，减轻计算压力，便于并行求解。但由于电力网络的不确定性，该方法无法满足求解要求，因此在该方法基础上提出单、双边块对角变换法（singly/doubly bordered block diagonal form，SBBD/DBBD）［12］，下面依次介绍这两种分块方法。

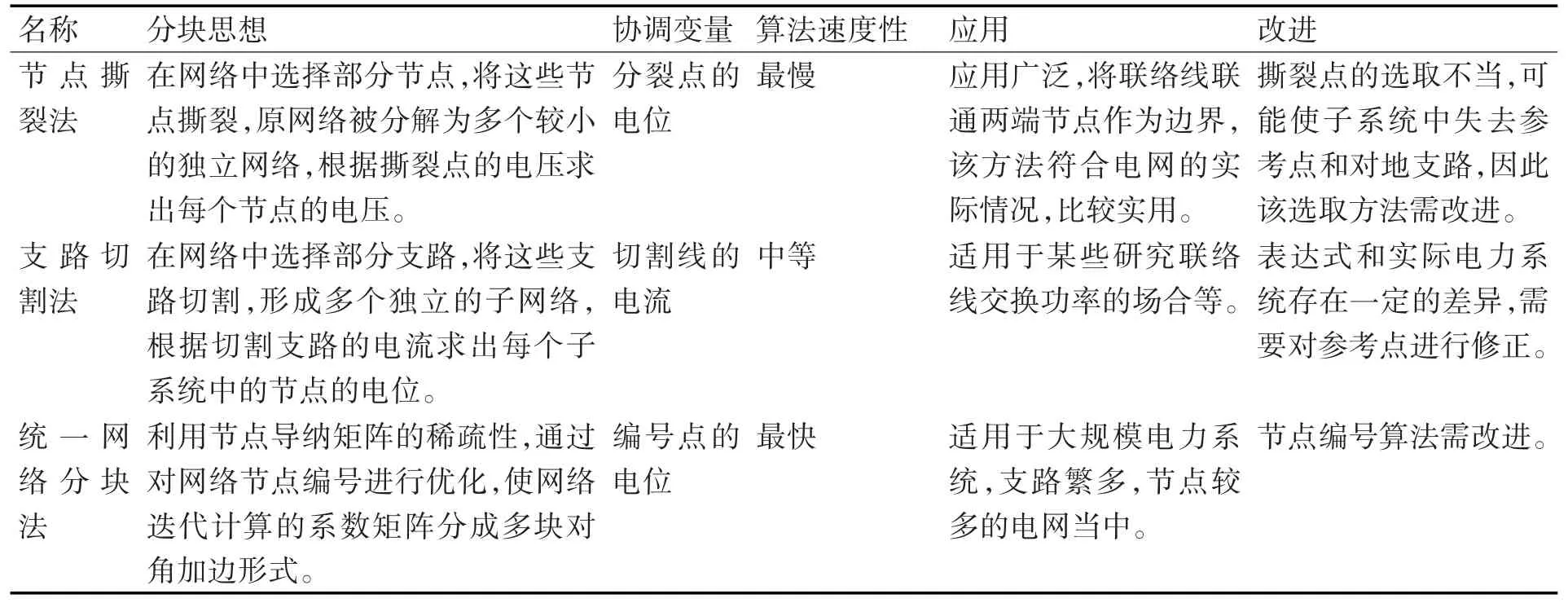
表2 BBDF中矩阵分块方法的对比

（1）对A进行双边块对角DDBD变换

对矩阵A进行变换后转置，则DBBD的表现形

式为

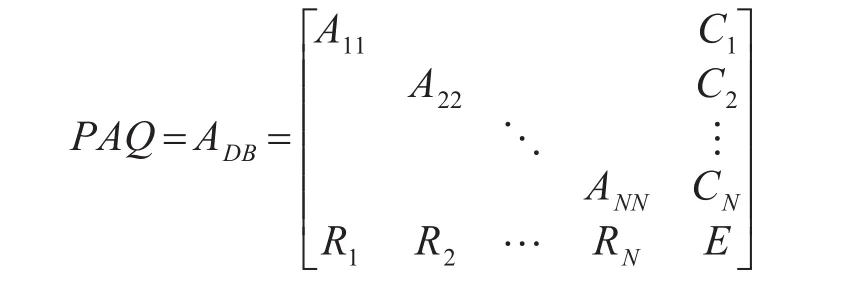
其中块 A11，A22，…，ANN是nN×nN，边界矩阵C1是n1×p矩阵，R1是 p×n1矩阵，且 p≤n。边界块中的每一列叫做耦合列，每一行叫做耦合行，对A进行DDBD变换时，只有当耦合行和列中的 p很小时，才能满足协调矩阵All之间的协调性。其中A矩阵中的元素aij需要满足的边界条件是， 门 槛 值u∈(0，1)。采用该方法，容易忽略列边界条件，导致u无法满足条件，矩阵变换失败。因此，只有在不消除边界条件的前提下，通过移动行、列的位置，DBBD的变换方式才有效。

（2）对A进行SBBD变换

采用DBBD变换时，移动矩阵行列会增加矩阵的维数，增加方程组求解的迭代次数。为了简化求解方法，对矩阵进行更进一步变换，即SBBD变换，其表现形式如下：

其中块 All是 ml×nl矩阵，ml＞nl，且边界矩阵为ml×p(p≤nl)，矩阵 A中的元素aij需要满足的边界条件是，在进行变换时，应尽可能减少耦合列的数量以保证分解块的稳定性。

4 潮流计算线性方程组求解并行算法

线性方程组并行求解最常用的处理方法有共轭梯度法，不完全Cholesky预处理共轭梯度法，重开始广义极小残差法等。下面分别对这些并行算法进行介绍。

4.1 共轭梯度法

共轭梯度法（Conjugate Gradient，CG）［13］也称共轭斜量法，是求取正定线性方程组首选方法。该方法最大的特点为当求解的线性方程组阶数很高时，通常只需经过比阶数小很多的迭代次数，就可以取得方程组的解。其算法描述如下：

对于 Ax=b线性方程，输入 A，b，其中 A为n×n矩阵，b为n阶向量，输出x

1）给定初值 x(0)=0，d(0)=0，r(0)=-b，迭代精度 ε＞0；

2）在第k次迭代时，求取x(k)分五步：

（1）计算残向量：r(k)=Ax(k-1)-b；

（2）计算修正方向向量：

（3）计算迭代步长：

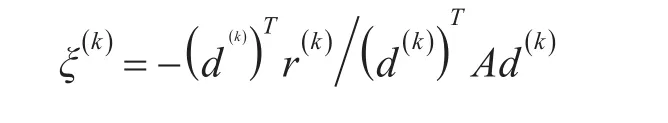
（4）求出新近似量：x(k)=x(k-1)+ξ(k)d(k)；

（5）如不满足迭代精度要求，则重复以上步骤。

该算法适用于A为正定矩阵的情况，若A为非对称非正定矩阵，LDLT分解矩阵不一定存在，使用该算法可能会导致程序中断。

为了满足实际需求，求解更大规模的线性方程组，可在共轭梯度算法上加入不同种类预处理。下面介绍一种常见的预处理方法，即不完全Cholesky预处理共轭梯度法（Modified Incomplete Cholesky Preconditioner Conjugate Gradient，MIC PCG）［14］，算法和PCG基本一致，这里不再赘述。

MIC PCG较PCG相比，迭代次数显著减少，在进行向量内积运算时，共享内存和全局内存达到最优，能够提高2倍以上的加速比。

4.2 广义极小残差法

重开始广义极小残差法（Generalized Minimal Residual Method，GMRES）［15～16］是 krylov子空间法的一种算法，是求解大规模线性方程组最受欢迎的一种，具有收敛速度快且比较稳定的特征。该算法能很好地在GPU上并行求解方程组，通过对显存中线程块、线程数的合理分配，使得每个线程能够同时并行求解方程，达到性能最优。

其算法描述如下：

对于 Ax=b线性方程，输入 A，b，其中 A为n×n矩阵，b为n阶向量，输出x

1）给定初值 x(0)=0，r(0)=-b，迭代精度ε＞0；

2）选取合适的m，使用Arnoldi迭代方法求?得Vn和，其中m是标准正交基向量的个数，Vn是由标准正交基组成的m×n矩阵，H~n是(n +1)×n阶的上Hessenberg矩阵；

3）极小化残余量范数，即 ‖H~nyn-βe1‖，求取使残余量范数最小的 yn。其中 β=‖b- Ax0‖，e1=(1 ，0，…0 )；

4）根据 xn=Vnyn，求得 xn；

5）如不满足迭代要求，则重复以上步骤。

根据以上算法，可以得出每次迭代所需要的计算次数以及它的复杂度，设矩阵A为n×n阶稀疏阵，m个标准正交基，每行有k个非零元，则可以得出表3。

从表中可以看出，稀疏矩阵与向量乘积、向量内积与范数在整体运算中是最耗时间的。当k比m 2+1大时，稀疏矩阵与向量乘积运算主要影响整个程序的性能，当k比m 2+1小时，向量乘积与范数运算主要影响整个程序的性能。考虑到在GPU运算过程中，向量内积与范数运算的瓶颈比稀疏矩阵与向量乘积运算少很多，因此加速效果主要受m大小所影响，m越大加速效果越好。但受浮点精度的影响，m不宜取值过大，取值过小又会导致收敛停滞。通常根据GPU的性能、系数矩阵A的特征、浮点精度的大小等因素折中选取合适的m值。表4对上述并行算法进行了比较。

表3 每次迭代中不同计算所需的计算次数和复杂度

表4 并行算法性能比较

5 结语

本文讨论对比了电力系统潮流并行计算中方程组的常用求解方法。其中，稀疏矩阵压缩算法适用于节点间物理连线较少的电力系统，可通过压缩矩阵来节省显存存储空间，提高并行速度；矩阵分块算法能进一步降低问题粒度，便于在GPU上实现多线程块并行求解线性方程组，提高并行化效率；线性方程组并行算法，通过预处理降低条件数来提升收敛速度，并在迭代求解过程中实现矩阵与向量内积等的并行计算，实现求解效率的有效提升。

目前已有很多较为有效的电力系统潮流并行计算方法，但由于潮流并行计算方程组的求解是一个比较复杂的问题，也还存在许多尚待进一步完善和解决的问题。如求解线性方程组时，在迭代次数减少的同时，如何解决收敛性能变差的问题；如何通过线程块的合理划分，保证二者之间的平衡性，达到性能最优的问题；如何在降低时间复杂度的情况下，进行网络中大型矩阵压缩算法的合理混合使用的问题；以及对方程组并行求解添加预处理算法来提高并行效率等等，这些将是未来需要进一步研究的方向。

［1］Hoang-Vu Dang，Bertil Schmidt.The Sliced COO Format for Sparse Matrix Vector Multiplication on CUDA enabled GPUs［J］.Procedia Computer Science，2012，9：57-61.

［2］李佳佳，张秀霞，谭光明，等.选择稀疏矩阵乘法最优存储格式的研究［J］.计算机研究与发展，2014，51（4）：882-888.LI Jiajia，ZHANG Xiuxia，TAN Guangming，et al.Study of Choosing the Optimal Storage Format of Sparse Matrix Vector Multiplication［J］.Journal of Computer Research and Development，2014，51（4）：882-888.

［3］商磊.大规模线性方程组求解的并行算法及应用［D］.西安：西北工业大学，2007，20-23.SHANG Lei.Parallel Algorithms and Applications for Solv⁃ing Large scale Linear Equations［D］.Xi'an：Northwest Polytechnic University，2007，20-23.

［4］阳王东，李肯立.基于HYB格式稀疏矩阵与向量乘在CPU+GPU异构系统中的实现与优化［J］.计算机工程与科学，2016，38（2）：205-206.YANG Wangdong，LI Kenli.Implementation and Optimiza⁃tion of HYB based SPMV on CPU+GPU Heterogeneous Computing Systems［J］.Computer Engineering&Science，2016，38（2）：205-206.

［5］薛巍，舒继武，王心丰，等.电力系统潮流并行算法的研究进展［J］.清华大学学报（自然科学版），2002，42（9）：1194-1199.XUE Wei，SHU Jiwu，WANG Xinfeng，et al.Advance of parallel algorithms for power flow simulation［J］.J Tsingh ua Univ（Sci&Tech），2001，42（9）：1193-1199.

［6］杨挺，向文平，王洪涛，等.电力系统对角加边模型的数据中心求解方法［J］.中国电机工程学报，2015，35（3）：512-514.YANG Ting，XIANG Wenping，WANG Hongtao，et al.An Algorithm for Solving the Block Bordered Diagonal Form of Electrical Power System in Data Center［J］.Proceedings of the CSEE，2015，35（3）：512-514.

［7］朱永兴，张步涵.电力系统潮流分解协调并行计算［J］.电力系统及其自动化学报，2010：22（5）.ZHU Yongxing，ZHANG Buhan.Decomposition and Coor⁃dination Power Flow Parallel Calculation［J］.Proceedings of the CSUEPSA，2010：22（5）.

［8］张伯明，陈寿孙.高等电力系统网络分析［M］.北京：清华大学出版社，1996：144-165.ZHANG Boming，CHEN Shousun.Network Analysis of Ad⁃vanced Power System［M］.Beijing：Tsinghua University Press，1996：144-165.

［9］黄彦全，肖建，刘兰，等.基于支路切割方法的电力系统潮流并行协调算法［J］.电网技术，2006，30（4）：21-22.HUANG Yanquan，XIAO Jian，LIU Lan，et al.A Coordina⁃tional Parallel Algorithm for Power Flow Calculation Based on Branch Cutting［J］.Power System Technology，2006，30（4）：21-22.

［10］龚仁敏，张永浩，翟学峰，等.面向整定计算的大型电力网络分块计算的实用化通用计算方法［J］.电力信息化，2007年增刊：42-44.GONG Renmin，ZHANG Yonghao，ZHAI Xuefeng，et al.A Practical General Method of Large Scale Power Net⁃work Partition Computing for Setting Calculation［J］.Electric power Information，2007 Supplement：42-44.

［11］陈珩.电力系统稳态分析［M］.3版.北京：中国电力出版社，2007：160-163.CHEN Heng.Steady-State Analysis of Power System［M］.The Third Release.Beijing：China Electric Power Press，2007：160-163.

［12］Iain S.Duff，Jennifer A.Scott.Stabilized block diagonal forms for parallel sparse solvers［R］.Council for the Cen⁃tral Laboratory of the Research Councils，2004.

［13］吴长江.基于CUDA的大规模线性稀疏方程组求解器的设计［D］.成都：中国电子科技大学，2013：27-30.WU Changjiang.Design of the of the solver for large scale linear sparse equations based on CUDA［D］.Chengdou：University of Electronic Science and Technol⁃ogy of China，2013：27-30.

［14］Jiaquan Gao，Ronghua Liang，Jun Wang.Research on the conjugate gradient algorithm with a modified incom⁃plete Cholesky preconditioner on GPU［J］.J.Parallel Dis⁃trib.Comput.74，2014.

［15］Kai He，Sheldon X.-D.Tan，Hengyang Zhao，et al.Par⁃allel GMRES solver for fast analysis of large linear dy⁃namic systems on GPU platforms［J］.INTEGRATION，the VLSI journal，2016（52）.

［16］张慧，于春肖，白雪婷，等.Krylov子空间E-变换GMRES（m）算法［J］.辽宁工程技术大学学报（自然科学版），2014，33（9）：1290-1291.ZHANG Hui，YU Chunxiao，BAI Xueting，et al.E-transform GMRES（m）algorithm based on krylov sub⁃space［J］.Journal of Liaoning Technical University（Natu⁃ral Science），2014，33（9）：1290-1291.