□潘云超　武瑞雪

（江苏省睢宁高级中学北校，江苏睢宁 221200）

高三数学一轮复习，主要是引导学生系统复习以前所学过的基础知识、基本技能、基本思想、基本方法，教会学生解决基本题型、自主复习、整理错题集，并合理利用“错解资源”提高学生的解题规范性，培养学生解题后反思的习惯等，即让学生掌握基础知识、基本的解题方法、复习的方法是高三数学一轮复习的重中之重.所以，高三数学一轮复习应重视以下三个问题.

一、重视回归“教材”落实“基础”

教材是落实基础的最好资料，是学生获得完整的系统的数学基本知识的源头，而基础知识、基本技能和基本思想方法是提高解题能力的“根”，所以必须重视回归“教材”，落实“基础”，让学生“地毯式”地深读教材，力争每个定理都会证（新课标中未要求的除外），要知其然且知其所以然；对基础知识的来龙去脉做到胸有成竹，对涉及的数学思想方法理解透彻，力争不留知识或方法盲点.为了提高学生的复习兴趣，可将基础知识“题目化”，且题目应尽量源于教材并高于教材，千万不要去搞难、偏、怪题，如复习函数、映射概念时，可编制如下题目.

（1）区别函数概念与映射概念.

（2）练习1 观察下列从集合A到B的对应：

①A=｛1，4，9｝，B=｛1，3，2｝，对应法则f：求算术平方根；

②A=｛1，4，9｝，B=｛2，3｝，对应法则f：求算术平方根；

③A=｛1，4，9｝，B=｛-3，-2，-1，0，1，2，3｝，对应法则f：求平方根；

④A=｛2，3，0，-2，-3｝，B=｛0，4，9，10｝，对应法则f：求平方；

⑤A=｛1，3｝，B=｛2，4，6｝，对应法则f：乘以2；

⑥A={平面a内的三角形}，B={平面a内的圆}，对应法则f：作三角形的外接圆.

则其中是集合A到B的函数有____；是集合A到B的映射有____（.填序号）

（答案：①④⑤；①④⑤⑥）

练习2 设集合M={-1，0，1}，N={1，2，3，4，5}，映射 f:M→N满足条件“对任意的x∈M，y=x+f(x)是奇数”，这样的映射 f有____个.

（答案：12）

练习3函数y=f(x)的图象与直线x=3有__个交点；与直线y=3有__个交点.

［答案：0或1；n（n∈N）］

答完上述各题，学生分别将函数、映射的概念及它们之间的区别与联系复习了一遍，并给予及时应用.

二、重视“就题论法”的解题教学 避免“就题论题”

案例1 设 f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x<0时，f'(x)g(x)+f(x)g'(x)>0，且g(3)=0.则不等式 f(x)g(x)<0的解集是____.

解记 φ(x)=f(x)g(x)，

由已知y=φ(x)为定义在R上的奇函数，φ(0)=0，且当x<0时，有ϕ'(x)>0，所以 y=φ(x)在（-¥，0）和（0，+¥）上均单调递增，且有 φ(-3)=φ（3）=0，画 y=φ(x)的图象草图，如图1，图象上包括点（0，0），得不等式 f(x)g(x)<0的解集为(-∞,-3)⋃(0,3).

如果到此结束，而不进行方法归纳总结，也不进行变式拓展，这种纯粹的“就题论题”式教学，会让学生无法顺利地将数学方法迁移，极易出现“教师一讲就懂，自己一做就不会”的“懂而不会”现象.

【方法总结】此题涉及的是抽象函数问题，既考查函数的奇偶性、单调性，又考查导数、不等式的性质等，可用“图形法”解决，让抽象的“数”的问题转化为具体的“形”的问题.

变式1（变换题目的结论）设 f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x<0时，f'(x)g(x)+f(x)g'(x)>0，且 g(3)=0.则不等式f(x)g(x)≥0的解集是___；f(x)g(x)>0的解集是____.

解 （解法同原题）得不等式 f(x)g(x)≥0的解集是[-3,0]⋃[3,+∞)；f(x)g(x)>0的解集是(-3,0)⋃(3,+∞).

变式2（变换题目的条件）设 f(x)是定义在R上的奇函数，当x<0时，xf'(x)-f(x)>0，且f(1)=0，则不等式 f(x)<0的解集是__；f(x)≥0的解集是___.

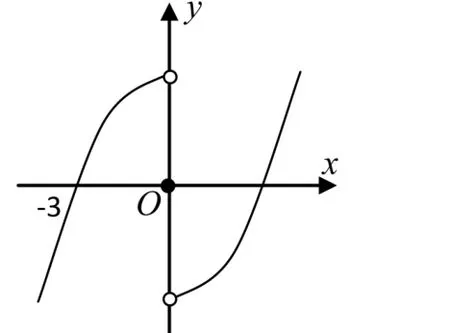
图1　

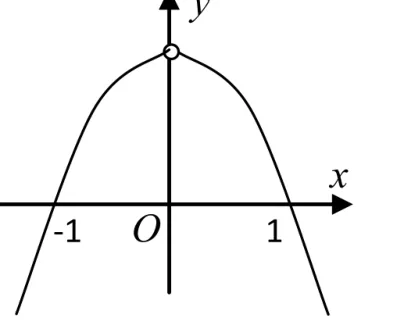
图2　

“就题论法”并进行适当“变式”的解题教学，利于加深学生对所涉数学方法的理解和掌握，并从“变”中寻求“不变”的解法本质，让学生触类旁通，举一反三，利于消除数学学习中“懂而不会”的现象.当然，无论是原题还是变式题，都应由学生独立思考，探究解法，切忌教师大包大揽、直接告知，其中的变式题也应由教师引导学生编制，这样才利于培养学生的解题能力和思维能力，否则，题目做得再多也是低效甚至是无效的.

三、重视对学生复习方法的指导

（一）教会学生“自主复习”基础知识，并对相关概念、结论进行对比

教会学生利用图表、填空等形式，将前后相关概念进行对比，让学生对这些概念的认识更深刻、更系统.如以相关的角的概念为例，可将直线的倾斜角、两条异面直线所成角、直线与直线所成角、斜线与平面所成角、直线与平面所成角、二面角、两向量夹角等进行系统复习，区别它们的概念、允许值范围等.

教会学生将教材上零散的、相关的知识建构成知识网络图，让学生对复习的知识有系统的、完整的、清楚的认识和理解，让学生能站在更高的层次，以更宽广的思路去分析问题、解决问题，能站在整体高度去审视教材，知道教材上每个知识点在具体解题时有什么作用.如在复习《立体几何》一章时，对于线线、线面、面面垂直的性质与判定，可引导学生建构如图3的知识网络图，让学生既见树木，又见森林.但是，值得注意的是，知识网络结构图不宜由教师直接呈现给学生，而应由教师引导学生、教会学生自行建构，培养学生勤于归纳的习惯和善于归纳的能力.

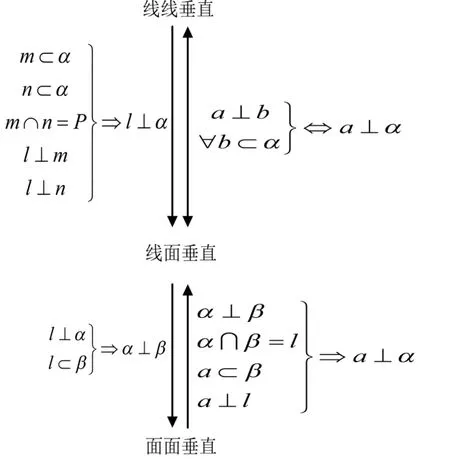
图3　

（二）教会学生自主剖析，整理错题本，能合理利用“错解资源”

进行解题教学时，对于易错题目，在课堂上应给予充分的展示与讲评，尽可能暴露完整的思维过程，让全班同学共享“错解资源”，要在剖析错误解法的过程中，让出错的学生充分经历由“误”到“悟”的思维过程.

错误解法的错因剖析透彻，并能记录在“案”，其教育教学的作用甚至要高于正确解法.所以，对于学生在练习或考试中易错的题目，一定要求学生整理在错题本上，写上题目、错解、错因、正解等.至此，学生疑惑不已，怎么会有bc=0？于是，有的学生认为此题为错题而放弃不做！

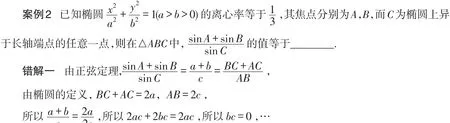
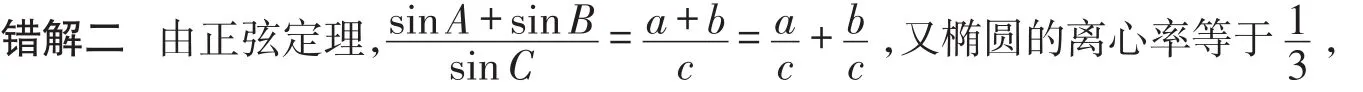
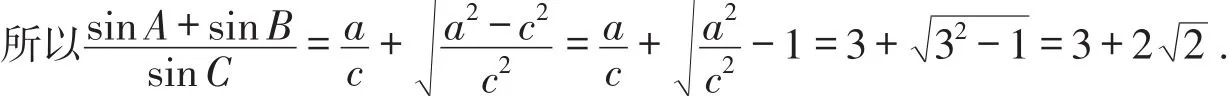
原因 将三角形的边a、b、c与椭圆中的a、b、c混淆，导致无法解出.为了区别三角形的边a、b、c与椭圆中的a、b、c，可借助下标或上标.

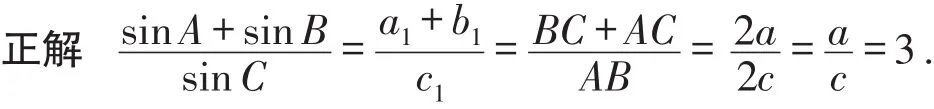
如果同一份试卷上某学生做错的题较多，为了节省时间，可要求学生在试卷上把错题做上标记，在旁边写上错因和正解，然后把试卷保存好，或粘贴在错题本上.整理错题集，一定要有恒心和毅力，而且要求学生每周末或每次考试前，把错题本或标记错题的试卷看一看，让其变成学生宝贵的复习资料.学生对于易错题经常性地复习，利于加深学生对错因的认识，利于增强学生对错误的“防御能力”，利于实现“听懂的就一定会做，会做的就一定做对，错过的就一定不会再错”的目标.

（三）教会学生“规范”解题

解题不规范是导致“会而不对”“对而不全”“估分与实际得分相差甚远”“难题不得分，易题好丢分”的重要原因之一.实践证明，在重要的考试中，每个人所表现的解题习惯与平时练习无异，所以，教学过程中，教师要以身作则，规范板书，并教会学生进行规范解题，注意叙述的条理性、结果的准确性．如不等式(x-2)(x-4)<0的解集，不能写为2

（四）教会学生进行解题后的“反思”

很多学生做过的题目不少，但解题能力提高缓慢，究其原因，一方面，是这些学生缺乏解题后主动反思的习惯，对题目涉及的数学思想方法的认识不深、理解不透；另一方面，有些教师的解题教学，也仅停留在让学生“知其然”的地步，缺乏让学生“知其所以然”的点拨，缺乏对学生解题后如何进行反思的指导.

案例3已知函数y=log2(x2-2ax+15)在(-∞,3)上为减函数，求实数a的取值范围.

解原函数可看作由y=log2t与t(x)=x2-2ax+15复合而成的，

而y=log2t是增函数，所以只要t(x)=x2-2ax+15在(-∞,3)上为减函数，

又t(x)=x2-2ax+15的对称轴为直线x=a，所以a≥3.

第一次反思——上述解法是否正确？

如果正确，有没有更简捷的解法？有没有需要完善的地方？

如果错误，是基础知识掌握不牢，在不该错的地方出错了？还是审题不清，忽视隐含条件或考虑不周？还是计算问题或图形画错？

通过反思，发现上述解法是错误的，忽视了函数y=log2t的定义域为(0,+∞).

正解原函数可看作由y=log2t与t(x)=x2-2ax+15复合而成的，

而y=log2t是(0,+∞)上的增函数，

所以只要t(x)=x2-2ax+15在(-∞,3)上为减函数，且t(x)>0在x∈(-∞,3)时应恒成立.

特殊地，在x=3时，t(x)可以取0，

所以a≥3且t(3)≥0，得实数a的取值范围应为[3 , 4].

第二次反思——怎样改编题目的条件，上述解法的思路才是正确的？

变式1已知函数y=2x2-2ax+15在()-∞,3上为减函数，求实数a的取值范围.

对于此道变式题，原解法的思路便是正确的，所求实数a的取值范围为[3,+∞).

第三次反思——反思地更深入些，“在(-∞,3)上为减函数”与“减区间为(-∞,3)”是否一样？

变式2已知函数y=2x2-2ax+15的减区间为(-∞,3)，求实数a的取值范围.

解原函数可看作由y=2t与t(x)=x2-2ax+15复合而成的，

而y=2t在R上为增函数，所以只要t(x)=x2-2ax+15的减区间为(-∞,3)，

又函数t(x)=x2-2ax+15的对称轴为直线x=a，

所以a=3，所以实数a的取值范围应为{}3.

变式3已知函数y=log2(x2-2ax+15)的减区间为(-∞,3)，求实数a的取值范围.

解原函数可看作由y=log2t与t(x)=x2-2ax+15复合而成的，

而y=log2t是增函数，所以只要t(x)=x2-2ax+15的减区间为(-∞,3)，且在xÎ(-∞,3)时恒有t(x)>0，又函数t(x)=x2-2ax+15的对称轴为直线x=a，

第四次反思——这3道变式题与原题“形似而神不同”，放在一起比较，能加深学生对题目涉及的数学思想方法的理解，既能让学生的记忆更久远，也利于培养学生思维的深刻性.

罗增儒教授把解题后不反思形象恰当地称为“入宝山而空返”.教师在一轮复习中，要有计划、有目的地指导学生进行解题后的反思，让解题后反思成为学生的一种习惯[1]，并能将这种习惯顺延到二轮、三轮复习当中去，让学生分析问题、解决问题的能力得以大幅度提高.□◢

参考文献：

［1］武瑞雪.重视解题教学提高教学效率［J］.数学教学研究，2011（11）：30-34.