邢治业

（山西工程职业技术学院 基础部，山西 太原 030009）

引言

考虑无约束最优化问题：

其中：f（x）是二阶连续可微函数.信赖域算法[1-4]是求解（1.1）式一类重要的数值计算方法，其基本思想为：在每一步迭代中，求解如下信赖域子问题：

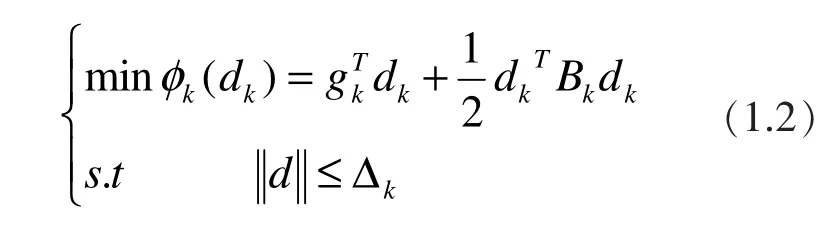
这里dk为所求子问题的解，其中Bk为f（x）在Xk处的Hesse矩阵或其近似；Δk是信赖域半径。

众所周知，将非单调技术应用于信赖域算法，算法结果取得良好的计算效果，并且加快了收敛速度。虽然传统的非单调技术存在很多优点，但也存在遗漏丢失最优迭代点等缺点，基于此，文章在文献[10]的基础上，利用新的非单调技术，并结合自适应技术和wolfe线搜索[5-7]，提出一种新的求解无约束优化问题的自适应信赖域算法。

1 算法的提出

在本节中，采用的新的非单调技术为[8-10]：

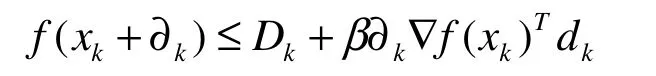
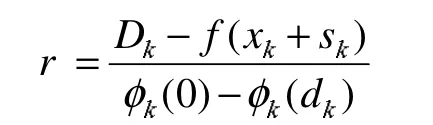
现在将新的非单调信赖域算法描述如下：

Step0：给定 x0∈Rn，B0∈Rn×n，Δ0＞0，令 β0＞0，0＜η1＜ω＜1，0＜μ1＜μ＜1，ε＞0，M≥1，令 k=0；

Step1：计算 gk，如果则停止；否则转 Step2；

Step4：若 r≥μ，令 xk+1=xk+dk否则求步长 ∂k，满足非单调wolfe线搜索：

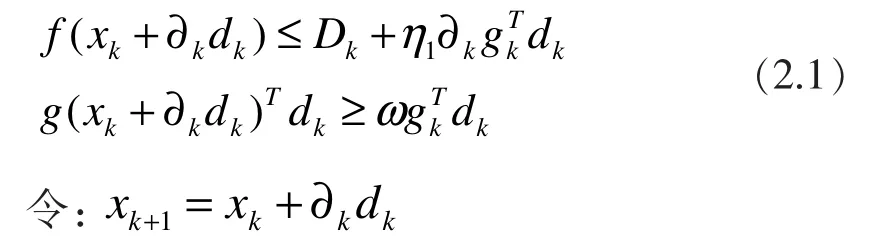
Step5：信赖域半径更新：

若：r≥µ,令

若：r<µ1,令

否则令∆k+1=∆k.

Step6：k=k+1，更新 Bk，若 ρk≥μ，则令 Mk+1=M+1，转Step1；

2 收敛性分析

为了分析算法的收敛性，我们作如下假设：

（A1）f（x）在水平集S上二次连续可微，且存在M≥0，使得

（A3）Δf（x）是 lipschitz连续函数即存在常数L＞0，使得：

引理 3.1[2]令dk是算法2.1产生的解，则有

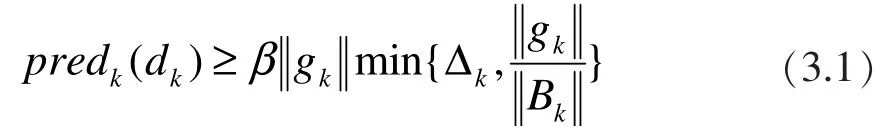
引理3.2若假设（A1）（A3）成立，｛xk］是算法产生的点列，则数列｛fl（k）｝非增且收敛。

证由m（k+1）≤m（k）+1及｛fl（k）｝的定义知fl（k+1）≤fl（k），所以｛fl（k）｝非增。由假设（A1）（A2）知有下界，而fl（k+1）≤fl（k），所以｛fl（k）｝收敛。

引理 3.3 算法产生的点列满足fk+1≤Dk+1≤fl（k+1）

证明：由fl（k）的定义可知fl（k+1）≥fk+1。

而fk+1=rk+1fk+1+（1-rk+1）fk+1≤rk+1fk+1+（1-rk+1）fl（k+1）=Dk+1。显然再由Dk的定义可得：fk+1≤Dk+1≤fl（k+1）

为了证明算法的收敛性，假设存在c＞0,使得dk满足

引理 3.4 若假设A1、A2、A3成立，则：

证明：易知算法2.1产生的迭代点满足：

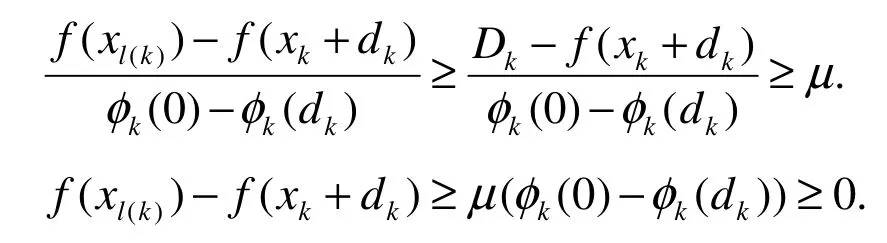
将上式k用l（k）-1来代替得：

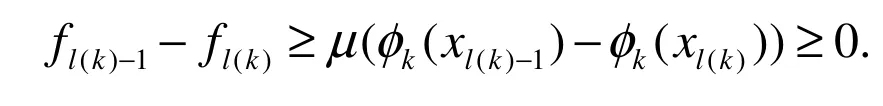
两边取极限并由引理3.2可得：

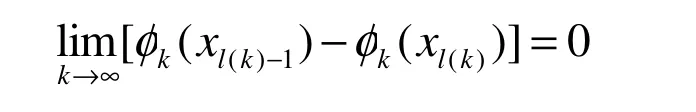
由引理3.1可知：

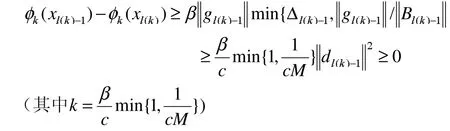
定理 3.5 若上述假设成立，给定初始点x0，初始对称阵Bk，设｛xk｝是由前述算法产生的迭代序列，则。

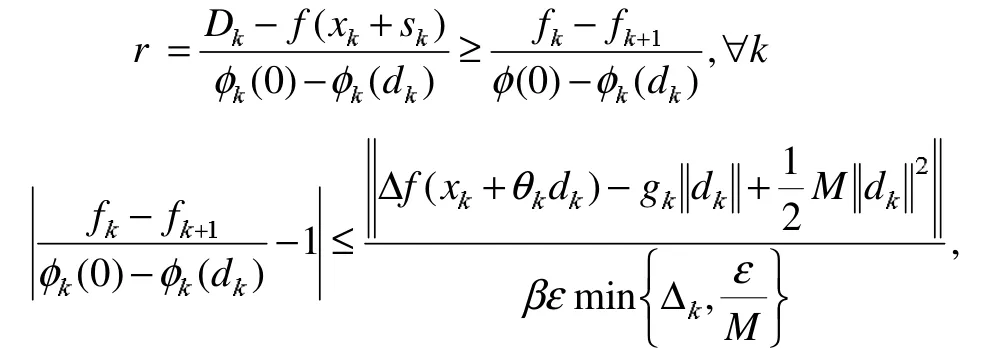
∀k（其中 θk∈（0，1））

故对充分大的 k，（Dk-fk+1）/predk≥μ≥μ1，由算法 2.1可知对充分大的k，Δk+1≥Δk。结合引理3.1可知，与3.2式矛盾，假设不成立，即，定理得证。