基于卡尔曼滤波和ISODATA的航标漂移预警方法
2018-01-10甘浪雄徐才云周春辉郑元洲陈润
甘浪雄+徐才云+周春辉+郑元洲+陈润


摘要:为解决目前航标遥控遥测系统中航标漂移误报警过多的问题,提出一种基于卡尔曼滤波和迭代自组织数据分析算法(iterative self-organizing data analysis technique algorithm,ISODATA)的组合优化方法。该方法如下:对航标GPS接收机原始坐标数据进行滤波,消除波动较大的数据后得到较可靠的航标位置数据;使用ISODATA得出其聚类中心;以该聚类中心取代航标抛设位置作为航标回旋中心,计算航标漂移距离。测试结果表明,该组合优化方法能够获取较为准确的航标漂移距离,在降低航标维护成本的同时,还能有效减少误报警。
关键词: 航标; 卡尔曼滤波; 迭代自组织数据分析算法(ISODATA); 误报警
中图分类号: U644.1 文献标志码: A
Abstract: In order to solve the too much false alarm problem of the buoy drift in the remote control telemetry system, a combinatorial optimization method based on Kalman filtering and the iterative self-organizing data analysis technique algorithm (ISODATA) is proposed. The method is as follows: the buoy initial coordinate data from GPS are filtered to eliminate the fluctuated data, and the reliable buoy position data are obtained; the clustering center of the data is got by ISODATA; the clustering center is used as the buoy motion center instead of the buoy throw position to calculate the buoy drift distance. The test results show that, by the combinatorial optimization method, the more accurate buoy drift distance can be obtained, and the buoy maintenance cost and false alarm are both reduced.
Key words: buoy; Kalman filtering; iterative self-organizing data analysis technique algorithm (ISODATA); false alarm
0 引 言
航标是帮助和指引船舶航行,标示航道方向、界限和碍航物的重要标志。航标能否正常运行,关系着船舶的安全航行乃至船员的人身安全。随着通信和网络技术的快速发展,GPS在航标位置监测方面得到了应用。但GPS的定位精度受多径效应、电离层延时误差等因素的影响。[1]若定位误差较大,则可能会频繁发出误报警,增加管理压力。要减少误报警,首先要采用适当的方法提高GPS定位精度。
目前,定位精度较高、技术较成熟的方法是差分GPS技术[2]:先利用已知精确坐标的差分GPS基准台解算出修正量,用户接收机利用该修正量对观测数据进行修正,从而得到较高精度的定位数据。差分技术的应用成本较高且受工作区的限制,因此有必要研究如何提高低成本的GPS自主式定位精度。目前,提高GPS自主式定位精度的方法主要是采用各类滤波算法对GPS接收机数据进行实时或事后处理。[3-4]张淑芳等[5]首次采用线性系统的识别方法和最小二乘法得到了准ARMA模型(auto-regressive and moving average model),对GPS输出数据进行实时建模与预测;常青等[6]提出在四星定位星座中增加第五颗星的选择方法,并以该方法和最小二乘递推估计为基础提出一种递推算法,提高了定位精度。杜晓辉等[7]使用卡尔曼滤波对GPS接收机数据进行处理,得到较小的估计误差,证明了卡尔曼滤波用于GPS静态单点定位的可靠性。在提高航标定位精度理论方面:林艺芳等[8]提出一种通过事先确定的基点来计算观测点与基点的距离进而实现航标GPS异常点判别的方法,该方法受主观因素影响较大;陈芹[9]采用基于距离的线性内插模型的伪距改正数算法来提高GPS定位精度;聂婧[10]将卡尔曼滤波引入航标系统中,对GPS观测数据进行平滑处理,有效地抑制了误差随时间累计逐渐发散的现象。然而,上述提高GPS定位精度的算法均停留在理论层面,并未考虑航标所处恶劣环境對航标定位造成的影响。刘胜等[11]首次提出一种基于卡尔曼滤波和FCM(fuzzy C-means)聚类的方法,并进行了相关试验,实现了GPS定位精度的提高。实现FCM聚类需要选择合适的平滑因子,但平滑因子的选取目前缺乏理论支持和有效性评价准则。DUNN[12]第一次提出应用模糊数学的迭代自组织数据分析算法(iterative self-organizing data analysis technique algo-rithm,ISODATA),通过不断修正聚类中心位置来实现分类。张丽娜等[13]采用ISODATA实现了数据结构复杂、离散度大的大样本数据的有效聚类。
本文先对影响航标漂移量的因素进行分析,对不同水深处、不同倾角的航标的漂移量进行理论计算,论证本文研究的必要性,然后采用卡尔曼滤波对航标GPS接收机数据进行滤波,滤除波动较大的数据,再对滤波后的数据进行聚类分析,得出其聚类中心。分别以该聚类中心和航标抛设位置为基准点计算航标漂移量并进行比较,验证方法的有效性,以期实现航标漂移有效预警和减少误报警。endprint
1 航标漂移量建模及误报警问题分析
1.1 航标漂移量建模
1.1.1 航标的回旋半径e1
航标是由系碇和锚链系留于水中的。国际航标协会(IALA)在1998年关于通用系碇系统设计的建议[14]中指出航标锚链布放长度与水深的关系:在一般情况下,水深小于50 m时航标锚链最小布放长度为水深的2倍,水深大于50 m时航标锚链最小布放长度为水深的1.5倍。以系碇为中心,航标的最大活动半径为回旋半径。设锚链长度为L,水深为D。理论上,回旋半径e1为e1=0.8 L2-D2
1.1.2 航标倾斜对GPS接收机的影响
GPS接收机天线通常安装在航标架上。假设在GPS无测量误差,无风、浪、流等影响的理想状况下,航标在水面上保持正立,GPS接收机天线与航标中心重合,此时GPS接收机测量到的位置即航标的中心位置。在风、浪、流等的作用下,航标会产生一定角度的倾斜,天线位置会偏离航标中心(见图1),此时GPS接收机测量到的位置会与实际中心出现偏差。设航标高度为H,航标倾斜角为θ,则其偏差e2大小为e2=Hsinθ
1.1.3 航标抛设时的定位误差e3
在进行航标抛设作业时,为提高航标布设的精度,航标船需要获取前甲板作业点准确的位置信息。目前,主要凭借驾驶人员经验和船载GPS天线位置、航速、航向等估算航标抛设点位置,设其误差为e3。这种方式存在定位误差大、无法准确记录航标布设位置等缺点。根据《海区航标效能验收规范(JT 759—2009)》,航标的推算系碇位置与设计位置误差值应小于30 m,本文假设e3≤15 m。
1.1.4 GPS定位误差e4
GPS的定位精度受很多因素影响,诸如卫星星历误差、卫星钟差、大气折射误差和接收机天线相位中心偏差等。目前民用GPS定位精度e4约为5~15 m。
1.1.5 漂移量建模
综上所述,假设水深为常量,航标漂移量理论计算模型为E=e1+e2+e3+e4=
0.8 L2-D2+Hsinθ+e3+e4
(3)1.2 航标漂移误报警问题分析
《东海海区航标配布规定(试行)》(以下简称《规定》)中指出,浮动标志位置与航道边线的横向距离通常以20~50 m为宜。参照该标准,航标的漂移报警阈值应不超过50 m。根据式(3),本文对不同水深(5~30 m)处、不同倾角的航标的漂移距离进行了计算,结果见图2。
由图2可知,随布设航标处水深的增加,航标漂移距离迅速增大。受各种误差的影响,图2中漂移距离大于50 m的点占所有计算点的比例为50%。若直接采用凭经验估计的抛设位置与GPS观测的原始数据来判断漂移距离是否超出要求值,必定会引起频繁的误报警。若采用增大报警阈值的方式来减少误报警概率,则当航道水深较大时报警阈值将大大增加,无法满足《规定》要求。因此,有必要采取措施来实现在不加大报警阈值的同时减少误报警。
2 GPS数据处理
2.1 卡尔曼滤波模型及数据处理
卡尔曼滤波是在对系统可观测信号进行测量的基础上,根据一定的滤波准则,采用某种统计量最优方法,对系统的状态进行估计的理论和方法,预测时具有无偏、稳定和最优的特点。[15]由于受到各种干扰的影响,GPS接收机的观测数据波动较大,不可直接使用。为了解决这个问题,采用卡尔曼滤波处理GPS接收机原始数据,得到比较可靠的定位数据,将滤波后的精度控制在可接受的范围内。
根据航标低动态运动特点,将其近似当作定常速度模型,以待测点的位置和速度作为状态变量。为便于处理观测数据,假定系统噪声和观测噪声为高斯白噪声,将其视为一个线性系统,采用卡尔曼滤波的方法进行数据处理。根据以上分析,定义状态变量为x=(x y x · y ·)
2.2 ISODATA确定坐标
经卡尔曼滤波得到較可靠的定位数据后,还需要确定用于计算漂移量的基准点,本文采用ISODATA来确定该基准点。ISODATA[13,16]是一种常用的聚类分析方法,它通过设置初始参数(初始聚类中心V,预期的聚类中心数目K,每一聚类域中应具有的最少样本数目θN,一个聚类域中样本距离分布的标准差θS,聚类中心之间最小距离θC,一次迭代中可以合并的聚类中心的最多对数L,允许迭代的最多次数I)引入人机对话环节,并使用合并和分裂等机制,其中:合并是当两类聚类中心距离太近时,将这两类合并为一类;分裂是当某类的类内样本距离分布标准差太大时,将该类分成两个类别。这样,根据随机给定的初始聚类中心和设定的类别数目等参数进行迭代,不断调整这些类别中心,直到得到最好的聚类中心,聚类结果能更加接近客观真实的聚类结果。
基于ISODATA的数据聚类分析流程见图3。
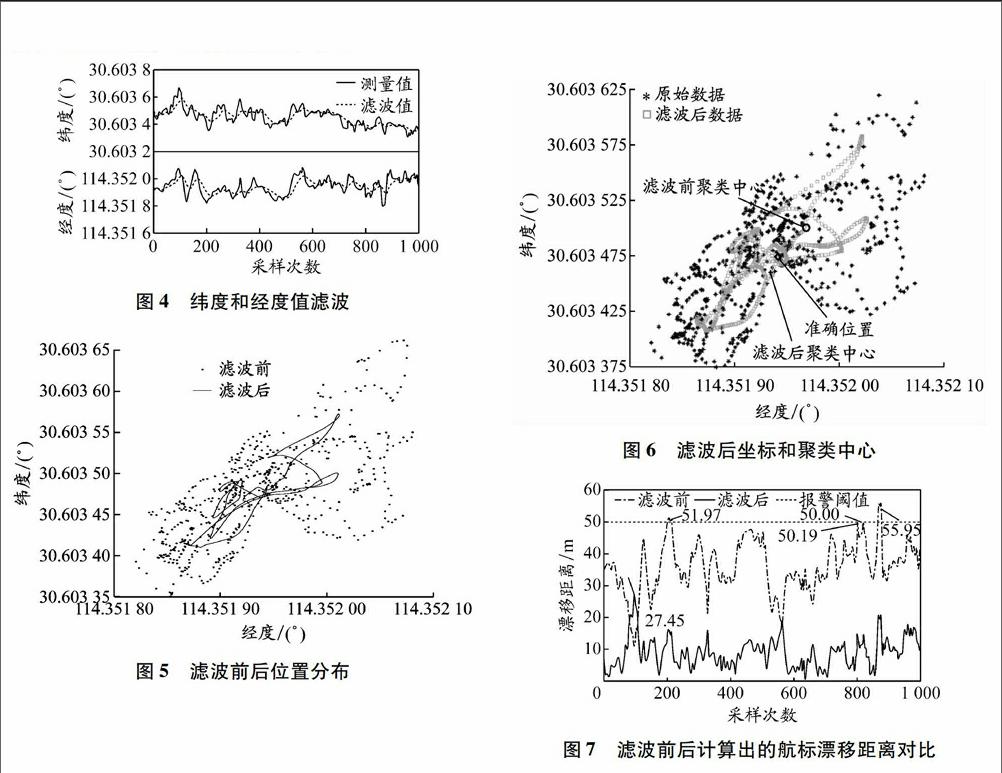
滤波的目的是对原始数据进行事后处理,剔除波动较大的数据。GPS接收机原始数据经卡尔曼滤波处理后,逼近所测位置的真实坐标。滤波后的数据在一个较小的区域内,要得到高精度的坐标位置,必须进一步进行数据处理。根据本文所述,无须对GPS数据进行分类,只确定其聚类中心即可。对滤波数据采用ISODATA进行聚类,结果见图6。
为便于比较滤波前后的聚类精度,试验前用高精度RTK设备测定GPS接收机的精确坐标。由图6可知,滤波后的聚类中心更接近GPS接收机真实位置,证明了利用该组合优化方法确定聚类中心的准确性。
3.2 滤波前后航标漂移距离及误报警分析
分别以航标抛设估算位置和采用组合优化方法后确定的聚类中心为基准位置计算航标漂移距离,报警阈值设为50 m。由图7可知:采用未经优化方法处理的数据,计算出的漂移距离平均值为35.87 m,在测试中触发了至少4次报警(报警后经现场确认,航标未发生漂失,因此其均为误报警),其中有131组数据计算值超过45 m,占所有数据的比例为13.1%;采取优化方法后,计算出的漂移距离平均值为8.796 m,最大值为27.45 m,报警次数为0。endprint
4 结 论
结合航标实际工作情况,提出基于卡尔曼滤波和ISODATA的航标GPS单点定位组合优化方法,利用在实际航标上搭载的GPS模块进行了相关试验。试验结果表明该方法可有效减少航标漂移误报警,验证了方法的准确性。用该方法可大大降低航标维护人力、物力成本,对提高航标管理效率、减轻管理人员压力及保障航行安全有重要意义。
参考文献:
[1] 游广芝. GPS导航定位中的误差分析与修正[D]. 哈尔滨: 哈尔滨工业大学, 2007.
[2] 付向斌, 戴亚文, 林金村. 航标灯多基站GPS伪距差分定位新方法[J]. 武汉理工大学学报(信息与管理工程版), 2011, 33(5): 735-737. DOI: 10.3963/j.issn.1007-144X.2011.05.015.
[3] TU Xianqin, MENG Qinghai, YI Dongyun, et al. Evaluation of kinematic airborne GPS data processing using precise point positioning approach[C]//International Conference on Computer Science and Electronics Engineering. IEEE Computer Society, 2012: 63-68.
[4] GAO Y. GPS positioning accuracy using precise real-time ephemeris and clock correction[J]. Marine Geodesy, 1994, 17(4): 279-288. DOI: 10.1080/15210609409379736.
[5] 张淑芳, 袁安存. 提高GPS定位精度的新方法[J]. 中国航海, 1997(1): 6-10.
[6] 常青, 柳重堪, 张其善. 基于最小二乘递推估计的GPS定位算法[J]. 北京航空航天大学学报,1998, 24(3): 15-18. DOI: 10.13700/j.bh.1001-5965.1998.03.005.
[7] 杜晓辉, 任章. 基于卡尔曼滤波的GPS静态定位精度分析[J]. 全球定位系统, 2008, 33(5): 47-51.
[8] 林艺芳, 李汪彪, 苏伟达, 等. 一种航标定位的GPS异常点快速判别及剔除方法[J]. 现代电子技术, 2008, 31(17): 4-6. DOI: 10.3969/j.issn.1004-373X.2008.17.002.
[9] 陈芹. 航标监控及GPS高精度定位方法研究[D]. 合肥: 合肥工业大学, 2012.
[10] 聂婧. 智能航标灯系统及其GPS定位算法研究[D]. 合肥: 合肥工业大学, 2012.
[11] 刘胜, 张青春, 张兰勇. 聚类算法的GPS静态单点定位方法[J]. 哈尔滨工业大学学报, 2012, 44(11): 71-74. DOI: 10.11918/j.issn.0367-6234.2012.11.014.
[12] DUNN J C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters[J]. Journal of Cybernetics, 1974, 3(3): 32-57. DOI: 10.1080/01969727308546046.
[13] 張丽娜, 姜新华, 那日苏. 基于改进的ISODATA算法的大样本数据聚类方法研究[J]. 内蒙古农业大学学报(自然科学版), 2013, 34(1): 133-137.
[14] 张志江, 张蓓敏, 乐奇博, 等. 不同环境下灯浮标锚链的布放长度计算[J]. 水运管理, 2016, 38(3): 25-27. DOI: 10.3969/j.issn.1000-8799.2016.03.008.
[15] 严浙平, 黄宇峰. 基于卡尔曼滤波的动目标预测[J]. 应用科技, 2008, 35(10): 28-32. DOI: 10.3969/j.issn.1009-671X.2008.10.008.
[16] 何霁, 滕奇志, 罗代升, 等. 一种改进的ISODATA算法及在彩色荧光图像中的应用[J]. 四川大学学报(自然科学版), 2007, 44(3): 563-568.DOI:10.3969/j.issn.0490-6756.2007.03.024.
(编辑 贾裙平)endprint
