陈 聪, 孙嘉庆, 危玉倩, 李定国

(海军工程大学， 武汉 330031)

【航空和航海工程】

舰船静态电场微分递推换算法的泰勒展开优化

陈 聪, 孙嘉庆, 危玉倩, 李定国

(海军工程大学， 武汉 330031)

针对舰船静态电场的微分递推换算法在递推换算过程中误差不断积累这一问题，提出运用泰勒展开定理对其优化。推导出垂向二阶偏导数与水平二阶偏导数的关系，将其代入泰勒二阶展开后的递推公式，然后利用拉格朗日五点插值法，求得水平二阶偏导数，实现对递推公式的优化。对改进前与改进后的微分递推法的换算精度进行仿真比较，结果表明改进后的微分递推换算法的换算精度更高，说明了泰勒展开法对其进行精度优化可行。

舰船静态电场；微分递推；深度换算；泰勒展开

随着舰船探测技术和隐身技术的发展，国内外对舰船静态电场的研究也越来越多，在这其中，舰船电场的深度换算作为掌握舰船静态电场分布的重要手段也越来越受到关注[1-3]。微分递推法从舰船静态电场换算问题中换算区域内无源无旋这一特征出发，通过寻找两相邻中间层之间的递推关系，在逐步递推中由一个测量平面上的电场分布特征得到一定深度平面上电场的分布特征，相比于电性模拟体法[4]和拉氏方程法[5]，微分递推换算法[6]的计算过程简单且同时适用于由远及近与由近及远两类换算问题。但由于在递推过程中，误差的累积效应也越来越明显，影响了换算结果的精度。泰勒公式作为一个重要的数学公式，广泛应用于各类数学、物理问题的近似逼近处理当中[7-8]，本文首先从换算区域内的物理规律入手，推导了换算区域内电场强度三分量的水平二阶偏导数与垂向二阶偏导数的关系，然后运用泰勒公式对递推公式进行泰勒展开，得到了改进后的递推公式，并进行了仿真验证，结果表明，经过泰勒展开改进后的递推误差要低于未修正的递推误差，从而说明了这一改进方法的可行性。

1 微分递推法简介

舰船静态电场的深度换算问题分为两类，一类是由近源平面向远源平面换算称为由近及远换算，如图1(a)所示；另一类则是由远源平面向近源平面换算称为由远及近换算。如图1(b)所示。以由近及远换算中电场强度的x分量Ex的换算为例，根据牛顿莱布尼茨公式，两中间层平面上的Ex值有如下关系：

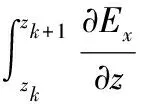
(1)

图1 换算示意图

若递推步长Δz足够小则有：

(2)

又测量平面与目标平面之间的换算区域内静态电场无源、无旋，所以：

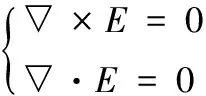
(3)

也即：

(4)

得:

(5)

代入式(2)可得：

(6)

类似得可以得到：

(7)

(8)

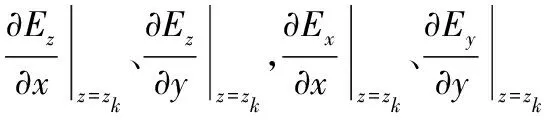
这一方法运算简单，实用性较强，但由于在逐步递推的过程中，换算误差的累积效应增大，降低了换算精度。

2 微分递推法的改进

为了提高微分递推法的换算精度，本文提出利用泰勒公式对递推公式进行二阶泰勒展开，来实现对算法的优化。仍以由近及远换算中电场强度的x分量Ex的换算为例,对式(2)进行二阶泰勒展开即有：

(9)

同理可得Ey和Ez的换算公式:

(10)

(11)

将式(5)所得结果代入式(9)、(10)、(11)得到:

(12)

(13)

(14)

与一阶导数相类似，只根据一个测量平面的测量值无法得到垂向二阶偏导数的初始值，因此必须找到垂向二阶偏导数与水平二阶偏导数的关系。

对式(5)等式两边对z求偏导，分别得到Ex，Ey，Ez对z的二阶偏导：

(15)

交换求偏导次序，结合式(5)得:

(16)

即得到了垂向二阶偏导数与水平二阶偏导数的关系，代入式(11)、(12)、(13)得到

(17)

(18)

(19)

根据二阶导数的五点公式[12]，结合测量平面上电场三分量的测量值，可以求得水平二阶偏导数的初始值，代入式(17)、(18)、(19)逐层递推得即可到待求平面上电场强度三分量的数值。

3 对改进效果的评价

在舰船静态电场的研究当中，国内外很多学者利用电偶极子模型对产生舰船静态电场的场源进行等效[10-11]。本文以一个水平电偶极矩为1 A·m的水平直流电偶极子在三层海洋模型中产生的电场模拟舰船静态电场，海水电导率设为4 S/m，海床电导率为0.4 S/m，选取大小为60 m×60 m的测量平面，按照图1所示建立坐标系(以海水-空气界面为xoy平面)，对改进后与改进前微分递推算法对两类换算问题的换算精度的改进效果进行研究。

3.1 对由近及远换算的改进效果

设定参数如表1，对改进前后由近及远换算的换算精度的变化进行研究。

表1 模拟参数设定

图2为未进行改进的微分递推法换算得到的待求平面上的电场强度的换算值与理论值在y=10 m处的曲线图，由图中可以看出，换算结果与理论值之间存在一定的误差，Ey与Ex的换算误差尤其明显。

图3为进行改进后的微分递推法换算得到的待求平面上的电场强度的换算值与理论值在y=10 m处的曲线图，由图中可以看出，换算结果与理论值契合的较好，相较于图2而言，换算值与理论值之间的差距大大减小。

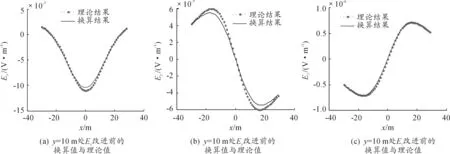
图2 y=10 m处改进前由近及远换算时电场强度三分量换算值与理论值

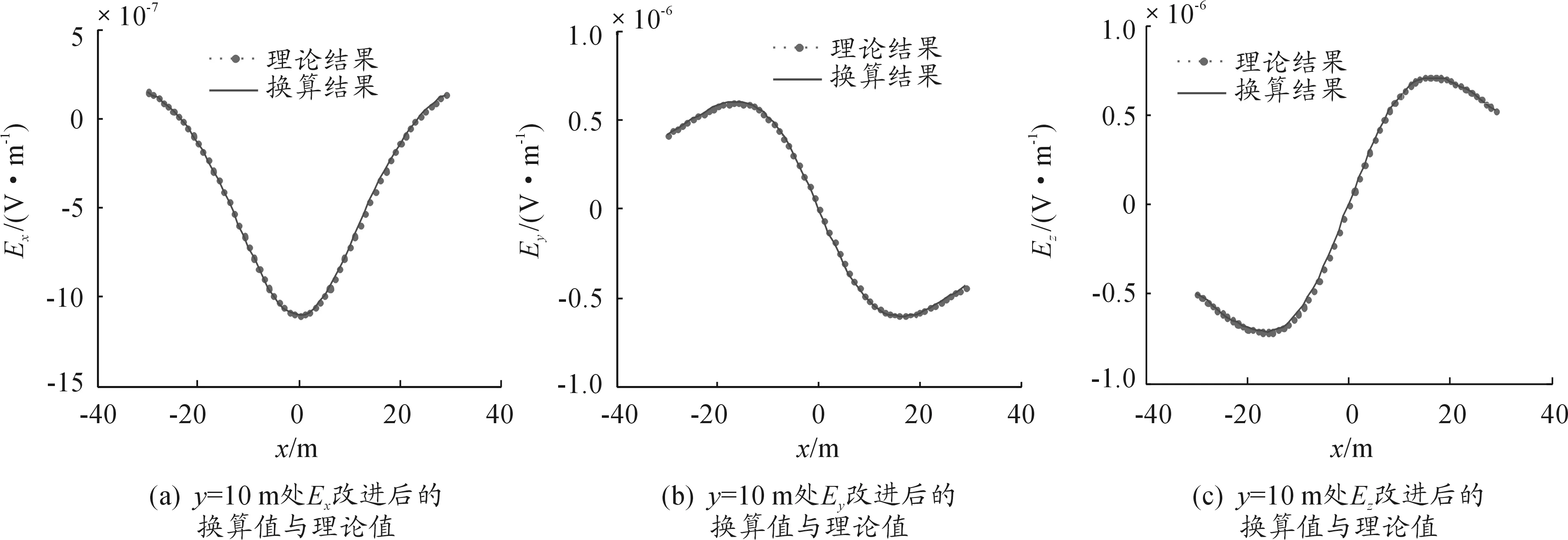
图3 y=10 m处改进后由近及远换算时电场强度三分量换算值与理论值

采用相对均方根误差对换算误差进行量化得到表2，由表2可以看出改进后的换算误差明显小于改进前的误差，这也说明了在当前换算参数条件下泰勒展开对微分递推法改进的可行性。

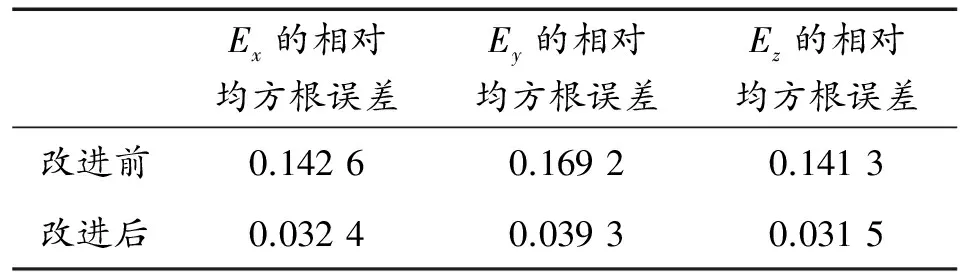
表2 由近及远换算中算法改进前后误差

为了进一步考察由近及远换算中泰勒展开改进后的递推算法取不同递推步长时的改进效果，保持表1中其他参数不变，分别取Δz为0.1 m、0.3 m、0.5 m、0.6 m、1.5 m、2 m、3 m，考察电场强度三分量的换算误差在换算前后的变化，得到图4。

由图4可以看出，当Δz小于0.6 m时，改进后的电场三分量换算误差大于改进之前;当Δz大于0.6 m时，改进后换算误差小于改进之前，且改进后换算误差维持在一个比较低的水平上。

这是由于用拉格朗日五点插值法所求的一阶水平偏导数值和二阶水平偏导数值与其理论值之间存在误差，且这一误差随着水深z的增大而减小。由近及远换算是由误差较大的一阶水平偏导数值和二阶水平偏导数值向误差较小的方向换算，一阶水平偏导数值和二阶水平偏导数值的误差积累的较快，当Δz小于0.6 m时，递推次数较多，由于改进算法引入了二阶导数的误差，递推次数越多，二阶导数的误差逐步累积，故改进效果不明显。但随着递推步长的增大，二阶导数误差的影响效果被弱化，换算精度得到改善，换算误差维持在一个较低的水平。

3.2 对由远及近换算的改进效果

设定测量平面位置为26 m，待求平面为20 m，Δz=-3(负号代表方向，以下均取其绝对值)维持3.1中其他参数设定不变，对泰勒展开优化后的微分递推算法的换算效果进行考察，得到图5，图6。

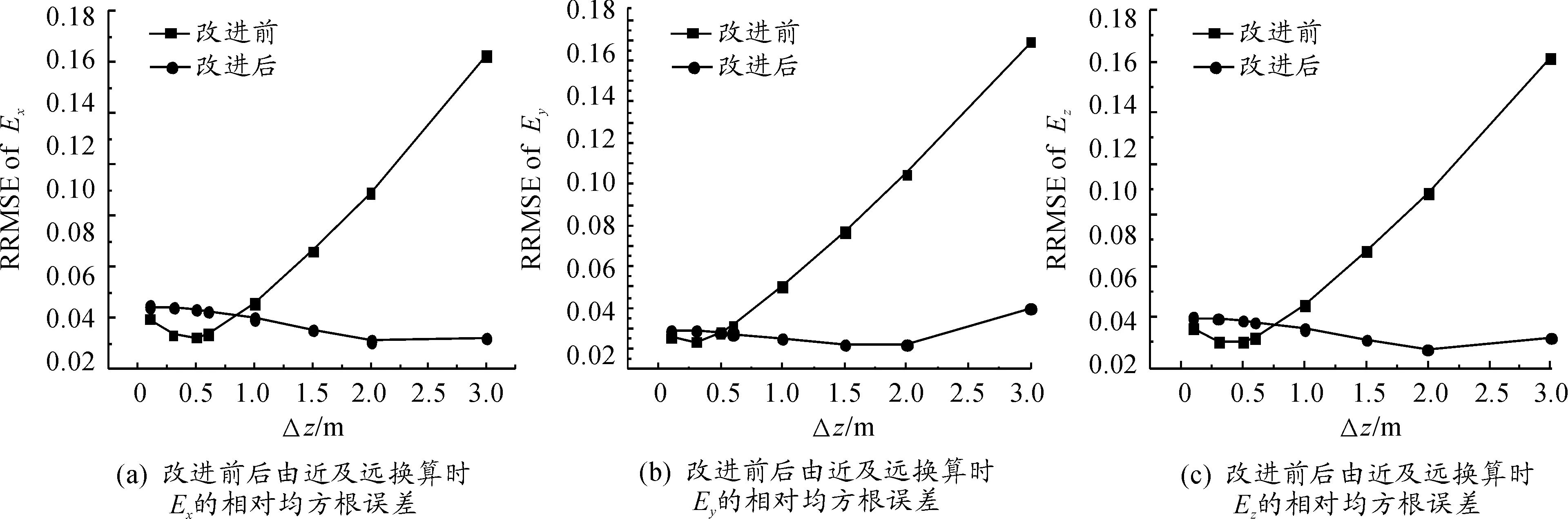
图4 改进后前后由近及远换算时电场强度三分量换算值与理论值

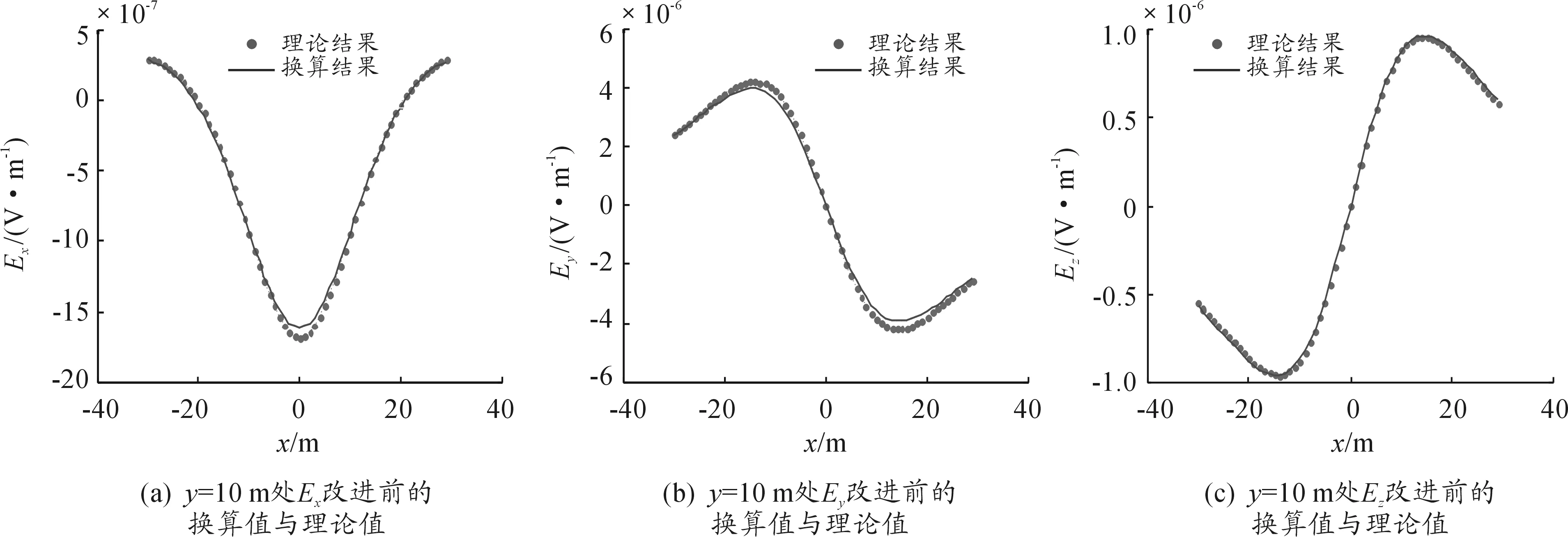
图5 y=10 m处改进前由远及近换算时电场强度三分量换算值与理论值

图6 y=10 m处改进后由远及近换算时电场强度三分量换算值与理论值

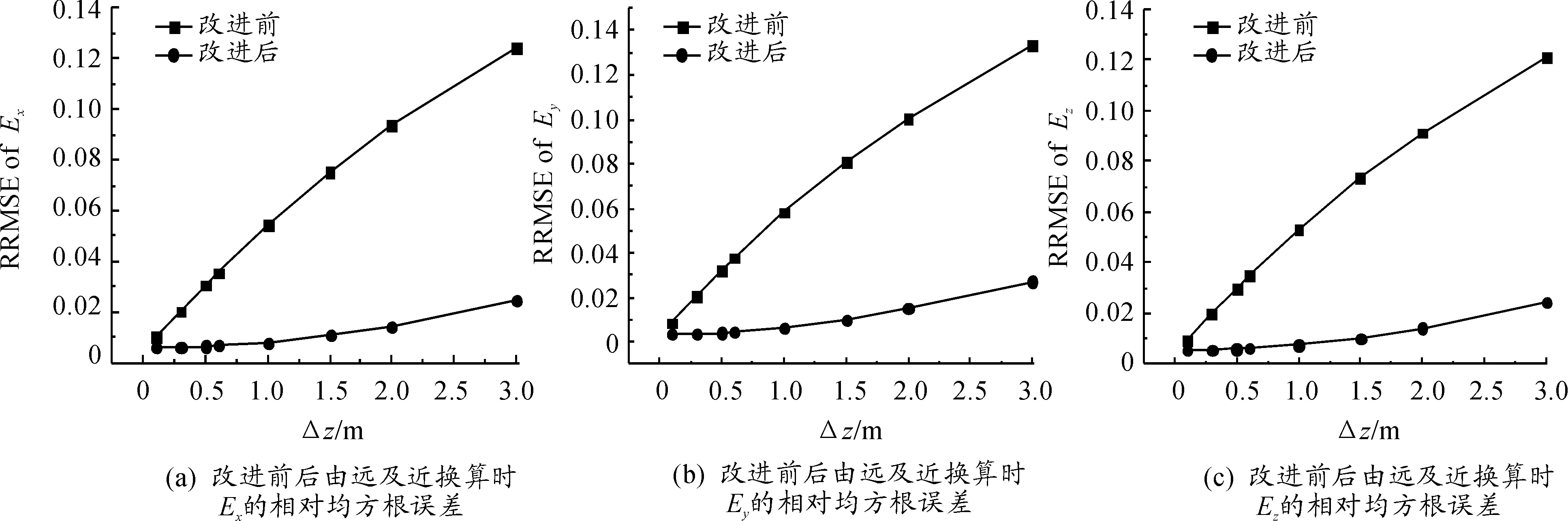
图7 改进前后由远及近换算时电场强度三分量换算值与理论值

对比图5、6，可以看出，在由远及近换算中，改进后的微分递推算算法的换算出的换算值与理论值的契合程度要优于改进之前。用相对均方根误差对换算误差进行量化，得到表3所得结果。

以相对均方根误差超过50%时的换算深度为极限换算深度，改进后由远及近换算的极限换算深度由改进前的40 m提升到49 m。进一步考察递推步长为0.1 m、0.3 m、0.5 m、0.6 m、1 m、1.5 m、2 m、3 m时泰勒展开对微分递推算法的优化效果，得到图7。由图7可以看出，由远及近换算时，改进后的微分递推法的换算误差始终小于改进前算法的换算误差。这是因为，与由近及远换算相比，由远及近换算是由误差较小的一阶水平偏导数值和二阶水平偏导数值得到误差较大的一阶水平偏导数值和二阶水平偏导数值，因此误差积累的较慢，二阶导数误差的引入对换算的影响较小。

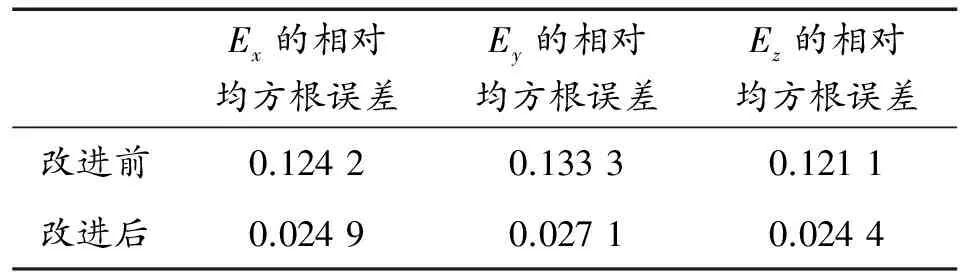
表3 由远及近换算中算法改进前后误差

4 结论

依据泰勒公式对微分递推法中离散化的递推公式进行泰勒展开，在理论上推导出水平二阶偏导数与垂向偏导数的关系，得到了改进后的递推公式，弱化微分递推法中误差的累积效应。仿真分析表明，改进后的微分递推算法用于舰船静态电场的深度换算时，换算精度更高，尤其是应用于由远及近的换算当中。但也可以发现，泰勒展开优化引入了二阶偏导数，而通过五点插值法求得的二阶偏导数值存在一定的误差，这使得泰勒展开法在解决误差累积效应问题中展现出了一定的局限性。为解决这一问题，今后的研究中，可以尝试采用理查德森外推法对五点插值法求导过程进行优化处理，以求获得更高的换算精度，从而弱化引入的二阶偏导误差的影响，提高其优化效果。

[1] 姜润翔,张伽伟,林春生.基于点电荷模型的腐蚀相关静电场快速预测方法研究[J].兵工学报,2017,38(4):735-743.

[2] 朱炜,郭航.现代舰船隐身技术的若干方法研究[J].舰船电子工程,2014,34(12):22-26.

[3] 何芳,王向军，高俊吉.基于边界元的舰船水下静态电场推算方法[J].探测与控制学报,2015,37(6):54-60.

[4] 陈聪,李定国,龚沈光.舰船静态电场深度换算方法[J].哈尔滨工程大学学报,2009,30(6):719-722.

[5] 陈聪,李定国,龚沈光.基于拉氏方程的舰船静态电场深度换算[J].电子学报,2010,38(9):2025-2029.

[6] 胡英娣，龚沈光，闫永贵.一种新的船舶静态电场深度换算方法[J].海军工程大学学报,2013,25(5):16-20.

[7] 唐克,谢保军,孙碧,燕峰.弹道修正弹修正力计算与仿真[J].四川兵工学报,2012,33(12):14-15.

[8] 黄辉,王忠思,年福耿.对数的近似计算方法[J].四川兵工学报,2009,30(7):55-57.

[9] 王燕.一阶导数的五点数值微分公式及外推算法[J].数学的实践与认识, 2011, 41(6): 163-167.

[10] 刘胜道.舰船水下电场的测试技术与电偶极子模型研究[D].武汉: 海军工程大学, 2002.48- 65.

[11] 刁爱民,杨庆超,王杏青.海水中电偶极子电场分布有限 元分析[J].四川兵工学报,2013,34(1):136-138.

[12] 王燕.二阶导数的五点数值微分公式及外推算法[J].天津理工大学学报,2009,25(4): 37-39.

TaylorExpansionOptimizationofDifferentialRecursiveAlgorithmforStaticElectricFieldofShips

CHEN Cong， SUN Jiaqing， WEI Yuqian， LI Dingguo

(Naval university of engineering, Wuhan, Hubei 330031, China)

In order to solve the problem of constant accumulation of errors in the recursive conversion algorithm for static electric field of ships, a Taylor expansion theorem was proposed to optimize the algorithm.The recursive formula of recursive conversion algorithm was put forward based on a second-order expansion of Taylor theorem,and the vertical second-order partial derivatives in the formula was converted to horizontal second-order partial derivatives which could be calculated by using the Lagrange five point interpolation method.In comparison of the improved recursive algorithm and the unimproved recursive algorithm,the simulation calculation was done, and result showed that the conversion accuracy of the improved recursive algorithm is higher than the unimproved one which showed the feasibility of the Taylor expansion method.

static electric field of ship; differential recursion; depth conversion; Taylor expansion

2017-09-05；

2017-09-30

国家自然科学基金资助项目(51109215)；学校科研发展基金自主立项(425517k101)

陈聪(1971—),女，博士，教授，主要从事水下军用目标特性及信息融合研究。

孙嘉庆(1993—)，男，硕士研究生，主要从事舰船水下电场目标特性研究。

10.11809/scbgxb2017.12.049

本文引用格式：陈聪, 孙嘉庆, 危玉倩, 等.舰船静态电场微分递推换算法的泰勒展开优化[J].兵器装备工程学报，2017(12):221-226.

formatCHEN Cong，SUN Jiaqing，WEI Yuqian，et al.Taylor Expansion Optimization of Differential Recursive Algorithm for Static Electric Field of Ships[J].Journal of Ordnance Equipment Engineering,2017(12):221-226.

TJ6

A

2096-2304(2017)12-0221-06

(责任编辑杨继森)