袁得春

(东北林业大学，哈尔滨，150040)

六自由度解耦机械臂的逆运动学通解

袁得春

(东北林业大学，哈尔滨，150040)

为求解六自由度解耦机械臂逆运动学通解，提出一种基于欧几里得范数的位姿分解逆运动学求解方法。先推导前3个关节角的解析解，快速、准确的获取机械臂的腕心位置；再利用已知的执行器姿态，计算后3个关节角，经六自由度机械臂的正逆运动学仿真互验，验证了方法的有效性。

六自由度，解耦机械臂，逆运动学通解

六自由度解耦机械臂是工业中常见的机械臂。其前3个关节控制机械臂腕心的位置，后3个关节的轴线交于腕心，控制机械臂末端姿态。该构型具有控制简洁、定位精度高等优点。正确建立机械臂正逆运动学模型是精确控制六自由度解耦机械臂的基础，逆运动学求解析解是其中最重要的问题。

国内外许多科研人员针对六自由度机械臂求逆解提出许多方法。Fu et al[1]78-82提出几何法求解机械臂的逆解，该方法需要绘制各杆件间的关系，计算效率偏低，不方便利用计算机求机械臂逆解。Paul et al[2]提出解析法求解六自由度机械臂的解析解，但其解法适用于机械臂各杆件相互平行或垂直的特殊构型机械臂逆运动学求解，是一种理想情况下的求解，在实际工程中，由于存在安装误差，无法保证机械臂杆件间的平行或垂直关系。故该方法不适于实际机械臂求解。徐文福等[3]针对空间漂浮机械臂的笛卡尔空间连续路径规划问题，提出基于速度级逆运动学求解方法。该方法利用雅可比迭代求机械臂逆运动学解，计算复杂度较高，效率偏低，不适于工程中对于高速机械臂逆运动学求解的要求。MIT讲义中给出了六自由度解耦机械臂逆解通解的结果，但并未给出证明过程。

本文提出一种六自由度解耦机械臂逆运动学通解的方法，它适用于任何非奇异构型的解耦机械臂求解，其速度和效率可以得到保证。并通过某型号着陆器机械臂的运动学实验验证该方法的正确性。

1 机械臂运动学原理

1.1 机械臂DH系建模

本文研究六自由度解耦机械臂，采用关节型串联构型，机械臂末端安装载荷(见图1)。采用Denavit-Hartenburg(D-H)方法对该机械臂的结构参数及各关节的运动学参数进行描述，建立相邻杆件固接坐标系之间的齐次变换阵。机械臂D-H系如图2所示，其中0系为底座系；机械臂D-H参数见表1。

表1 机械臂D-H参数

1.2 机械臂正运动学

机械臂正运动学，即给定机械臂6个关节角度的情况下，获得机械臂任意杆件上1点在其他坐标系下的位置。

图1 机械臂结构图

图2 机械臂D-H系

设λi=cosαi、μi=sinαi，可得D-H系的旋转变换阵(Qi)。

(1)

与投影关系得齐次变换阵(ri)。

ri=[aiC(θi)aiS(θi)bi]T。

(2)

可得D-H系的齐次变换阵(Ti)。

(3)

应用齐次变换阵的串接性质，可得机械臂末端相对于机械臂底座的齐次变换阵(T)。

T=T1·T2·T3·T4·T5·T6。

(4)

已知机械臂执行器l上任一点s位置rls，计算其在机械臂底座系下的位置。

(5)

1.3 机械臂逆运动学

1.3.1 由腕心位置求前3轴角度

工程中，机械臂末端的位置和姿态已知，故解耦机械臂逆运动学求解，需先根据机械臂末端姿态求出机械臂腕心位置，通过解析法求机械臂前3关节解，再求后3个关节的角度。

因坐标系0与坐标系1重合(见图2)，故r0=0、Q0=1。c表示腕心位置矢量在底座系下的表示。其定位方程为式(6)。

(6)

式中：腕心位置c=[xc，yc，zc]T为已知量。

1.3.1.1求θ3

对式(6)两端取欧几里得范数，

(7)

式(7)右式范数表示为：

定位方程(7)左式范数为：

(8)

图2所示的解耦机械臂，有a4=0，故有：

即：

2b2b3λ2+2b2b4λ2λ3+2b3b4λ3。

(9)

由式(8)及式(9)且左右范数相等得：

即：

2a1xcC(θ1)-2a1ycS(θ1)+(2a2a3-2b2b4μ2μ3)C(θ3)+

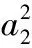
(10)

将式(10)表示为：

A·C(θ1)+B·S(θ1)+C·C(θ3)+D·S(θ3)+E=0。

(11)

因齐次变换阵第三行不含θ2，故有：

ycμ1C(θ1)-xcμ1S(θ1)-b4μ2μ3C(θ3)+a3μ2S(θ3)+

(12)

将式(12)表示为：

F·C(θ1)+G·S(θ1)+H·C(θ3)+I·S(θ3)+J=0。

(13)

其中衍生的结构参数：F=ycμ1；G=-xcμ1；H=-b4μ2μ3；I=a3μ2；J=b2+b3λ2+b4λ2λ3-(zc-b1)λ1。

联列式(11)、(13)得：

(14)

简化为：

(15)

(16)

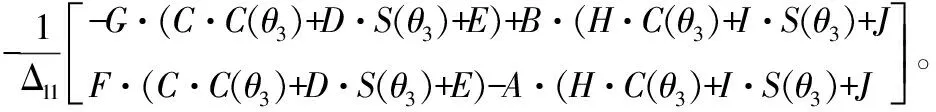
简化为：

(17)

1.3.1.2求θ1

因C2(θ1)+S2(θ1)=1，故可消元简化式(17)，得仅关于θ3的函数。

[-G(C·C(θ3)+D·S(θ3)+E)+B(H·C(θ3)+

I·S(θ3)+J)]2+[F(C·C(θ3)+D·S(θ3)+E)-

A(H·C(θ3)+I·S(θ3)+J)]2=(A·G-F·B)2。

简化为：

[(B·H-G·C)C(θ3)+(B·I-G·D)S(θ3)+

(B·J-G·E)]2+[(F·C-A·H)C(θ3)+

(F·D-A·I)S(θ3)+(F·E-A·J)]2=

(A·G-F·B)2。

(18)

对式(18)进一步处理得：

[(B·H-G·C)2+(F·C-A·H)2]C2(θ3)+[(B·I-G·

D)2+(F·D-A·I)2]S2(θ3)+2[(B·H-G·C)·

(B·I-G·D)+(F·C-A·H)(F·D-A·I)]·

C(θ3)·S(θ3)+2[(B·H-G·C)(B·J-G·E)+

(F·C-A·H)(F·E-A·J)]C(θ3)+2[(B·I-

G·D)(B·J-G·E)+(F·D-A·I)(F·E-A·

J)]S(θ3)+[(B·J-G·E)2+(F·E-A·J)2-

(A·G-F·B)2]=0。

(19)

将式(19)表示为：

K·C2(θ3)+L·S2(θ3)+M·C(θ3)·S(θ3)+

N·C(θ3)+P·S(θ3)+Q=0。

(20)

其中衍生的结构参数：

K=(B·H-G·C)2+(F·C-A·H)2；

L=(B·I-G·D)2+(F·D-A·I)2；

M=2[(B·H-G·C)(B·I-G·D)+(F·C-A·H)(F·D-A·I)]；

N=2[(B·H-G·C)(B·J-G·E)+(F·C-A·H)(F·E-A·J)]；

P=2[(B·I-G·D)(B·J-G·E)+(F·D-A·I)(F·E-A·J)]；

Q=(B·J-G·E)2+(F·E-A·J)2-(A·G-F·B)2。

简化为：

(21)

由式(21)得到关于τ3的4次方程：

(22)

其中τ3为式(22)的Gröbner基[4]：

由Cardano及其助手给出的一元三次和四次方程的根式解[5]，可以求得θ3的4个可能解。

若R≠0得：

若R=0、S≠0，式(22)退化为3次多项式方程。

若R=0、S=0，式(22)退化为2次多项式方程。

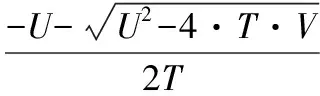
再将θ3的解带入(17)，得θ1解。

ifW+μ2·Z-yC·μ1=0∩xC·μ1>0∩W+μ2·Z+yC·μ1≠0;

ifW=0∩xC·μ1=0;

θ1=±π/2。

式中：W=b2+λ2(b3+b4λ3)-(zc-b1)λ1；Z=a3S(θ3)-b4μ3C(θ3)。

1.3.1.3求θ2

通过式(8)的前两个标量方程导出关于cosθ2、sinθ2的方程，得到θ2的解析解：

C(θ2)=(1/Δ22)[A11(xcC(θ1)+ycS(θ1)-a1)-A12(-xcλ1S(θ1)+ycλ1C(θ1)+(zc-b1)μ1)]；

S(θ2)=(1/Δ22)[A12(xcC(θ1)+ycS(θ1)-a1)+A11(-xcλ1S(θ1)+ycλ1C(θ1)+(zc-b1)μ1)]；

θ2=arctan(2(C(θ2),S(θ2)))。

式中：A11=a2+a3C(θ3)+b4μ3S(θ3)；A12=-a3λ2S(θ3)+b3μ2+b4μ3λ2C(θ3)+b4μ2λ3。

1.3.2 由末端姿态求后三关节角度

1.3.2.1求θ4

1.3.2.2求θ5

(23)

因式(23)第三列的第一与第二个分量独立于θ6，可得：

θ5=arctan2(C(θ5)，S(θ5))。

1.3.2.3求θ6

θ6=arctan2(C(θ6),S(θ6))。

2 机械臂正逆运动学互验

机械臂正运动学与逆运动学是互逆的行为。表2和表3中的数据显示：正逆运动学互验结果误差范围小于0.001°。

表2 腕心正逆运动学结果校验

表3 机械臂末端正逆运动学结果校验

3 结束语

森林作业机器人一直是国内外机器人研究的热点之一，本文提出一种基于欧几里得范数的位姿分解逆运动学求解方法，用来解决六自由度解耦机械臂通解问题。首先，推导前3个关节角的解析解，快速、准确的获取机械臂腕心的位置。之后，通过采样器的姿态，计算机械臂的后3个关节角。最后，通过自治机械臂仿真模型的正逆运动学互验结果证明该方法的正确性，为林业机器人的发展提供参考。

[1] FU K S， GONZALEZ R C， LEE C S G. Robotics control sensors vision and intelligence[M]. New York： McGrawHill，1987：78-82.

[2] PAUL R P， SHIMANO B， MAYER G E. Kinematic control equations for simple manipulators[J]. IEEE Transactions on Systems， Man， and Cybernetics，1981，11(6)：449-445.

[3] 徐文福，刘宇，强文义，等.自由漂浮空间机器人的笛卡尔连续路径规划[J].控制与决策，2008，23(3)：278-282，287.

[4] FATHI A， SHARIFAN N. A classic new method to solve quartic equations[J]. Applied and Computational Mathematics，2013，2(2)：24-27.

GeneralSolutionofInverseKinematicsofSixDegree-of-freedomDecouplingManipulator

Yuan Dechun

(Northeast Forestry University, Harbin 150040, P. R. China)Journal of Northeast Forestry University，2017,45(12)：88-92.

Six degree-of-freedom； Decoupling manipulator； General solution of inverse kinematics

袁得春，男，1985年4月生，东北林业大学机电工程学院，工程师，博士研究生。E-mail：8500284@qq.com。

2017年9月2日。

张 玉。

TH132.4；O311

In order to solve the general solution of inverse kinematics of the six degree-of-freedom (6DOF) decoupling manipulator, a decomposed position-orientation method based on Euclid Norm was presented. Firstly, the analytical solution of first three joint angles was deduced to calculate the wrist position of manipulator quickly and precisely. Secondly, the last three joint angles were solved by known executor’s orientation. By the inverse kinematic simulative simulation of the 6DOF manipulator, the effectiveness of method was verified.