陈 颖

(南通师范高等专科学校)

0 引言

1987年，Drinfeld在文献[1]中介绍了一类非常重要的Hopf代数，即拟三角Hopf代数. 拟三角性是Hopf代数的一个重要性质，具有广泛的应用价值. 一方面，拟三角Hopf代数上的泛 矩阵为著名的量子Yang-Baxter方程(见文献[2])提供了一类解；另一方面，在低维拓扑中也出现了某些特定的拟三角Hopf代数，它们和纽结以及3维流形的“量子不变量”有关，拟三角Hopf代数在量子群理论(见文献[3-5])中也占有非常重要的地位.

拟三角Hopf代数与Drinfeld偶(也称量子偶)之间的联系得到了进一步讨论. Radford在文献[6]中引入了极小拟三角Hopf代数的概念.有限维Hopf代数 的Drinfeld偶 就是一个极小拟三角Hopf代数. Radford证明了每个极小拟三角Hopf代数都是有限维的，而且一定是某个Drinfeld偶的商Hopf代数.

Larson和Towber在文献[7]中考虑了余拟三角双代数，证明了任给余拟三角(辫子)双代数(A,〈|〉)，都可以构造A的有限对偶A°的一个子双代数U〈|〉，这里〈|〉指的是A上的一个辫子. 这个构造推广了文献[8]中的结果. 2009年，Towber和Westreich在文献[8]中进一步证明了若U〈|〉是有限维的(即使A不是有限维)，则U〈|〉是一个Hopf代数，且是某个Drinfeld偶的商Hopf代数，从而是一个拟三角Hopf代数.

1 预备知识

关于Hopf代数的概念、符号和基本的理论，参考文献[3-5],下面回顾拟三角双代数的定义以及性质.

命题1 设(A,R)是拟三角双代数，则(id⊗ε)R=(ε⊗id)R=1A.

注1 设(A，R)是拟三角双代数，易证得R满足上循环等式

(R⊗1)(Δ⊗idA)(R)=(1⊗R)(idA⊗Δ)(R).

2 拟三角双代数的R-矩阵诱导的映射

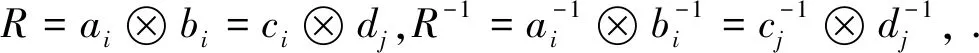
如下定义四个 线性映射：

命题2 设λ±，ρ±如上所述，则λ±是代数反同态，余代数同态；而ρ±是代数同态，余代数反同态.

命题3 设λ±,ρ±如上所述，则在卷积代数Hom(A°,A)中，下列等式成立

[λ+,ρ-]=[ρ-*λ+]=ε*1A，且

[ρ+*λ-]=[λ-*ρ+]=ε*1A.

命题4 设(A,R)是拟三角双代数，则下列结论成立：

(1)(Imρ+)(Imρ-)=(Imρ-)(Imρ+);

(2)(Imλ+)(Imλ-)=(Imλ-)(Imλ+),

其中，(Imρ+)(Imρ-)表示由所有形如ρ+(f)ρ-(g)的元素生成的k-线性空间，∀f,g∈A°；其余三个积的定义类似.

记B+=Imλ+，B-=Imλ-.可得，B+,B-都是A的子双代数，且作为域k上的线性空间都是有限维的，即B+是B-的有限维子双代数.

命题5B+和B-是对极可逆的Hopf代数.

命题6 令s+,s-分别表示Hopf代数B+,B-的对极，则下列结论成立:

(1)s+∘λ+=ρ-，且s-∘λ-=ρ+，

(2)Imλ+=Imρ-，且Imλ-=Imρ+.

定理1 设UR是A的由四个映射λ±,ρ±的像集生成的子代数，则UR=B+B-=B-B+，且UR是一个极小拟三角Hopf代数.

3 有限维Hopf代数UR的性质

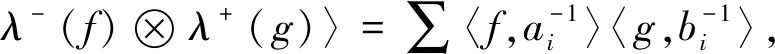
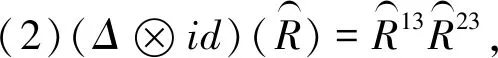
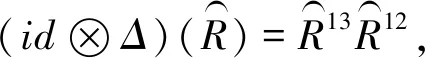
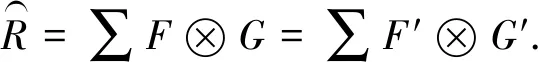
(3)设ε+,ε-分别是B+,B-的余单位，则

ε*(F)G=1(B+)*=(ε+)*,Fε*(G)=1(B-)*=(ε-)*,

进一步有，对∀f,g∈A°，

证明(1)设λ-(f)=λ-(f′),λ+(g)=λ+(g′), 则

即当λ-(f)=λ-(f′),λ+(g)=λ+(g′)时，则

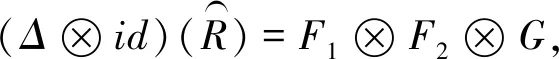
另一方面，又有

所以F1⊗F2⊗G=F⊗F′⊗GG′. 同理可证，F⊗G1⊗G2=FF′⊗G′⊗G.

(3)用id2⊗ε*作用于F⊗G1⊗G2=FF′⊗G′⊗G，可得

F⊗G=FF′⊗G′ε*(G)=Fε*(G)F′⊗G′.

又由于F⊗G可逆且F⊗G=F′⊗G;，故Fε*(G)=1(B-)*=(ε-)*.

同样，用ε*⊗id2作用于F1⊗F2⊗G=F⊗F′⊗GG′，可得

F⊗G=ε*(F)F′⊗GG′=F′⊗ε*(F)GG′,

故ε*(F)G=1(B+)*=(ε+)*.

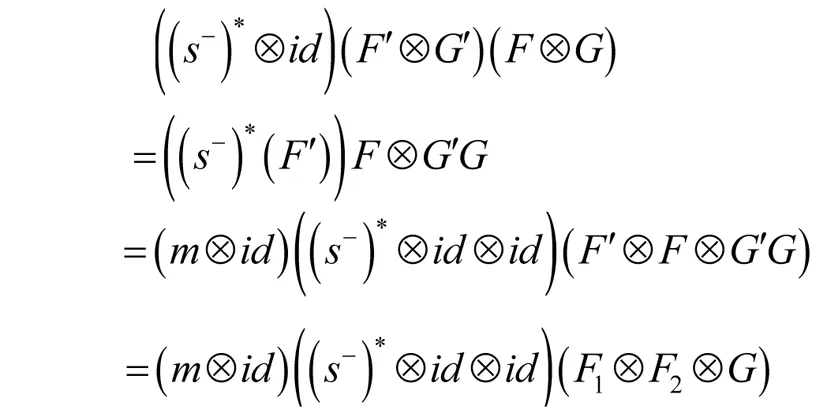
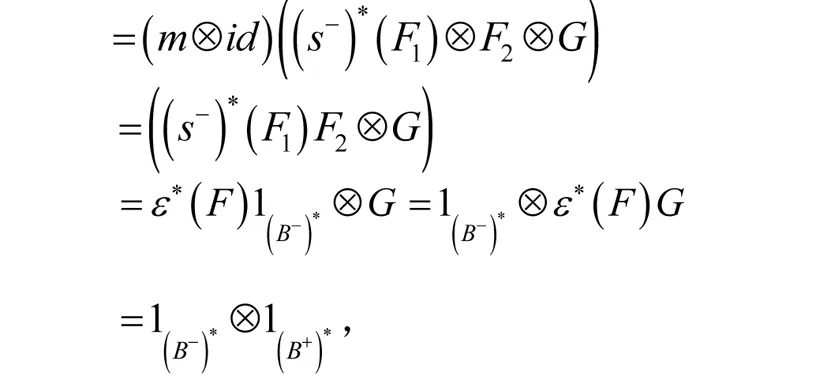
(4) 因为 所以，((s-)*⊗id)(F′⊗G′)是F⊗G的左逆元. 下面证明((s-)*⊗id)(F′⊗G′)是F⊗G的右逆元：

同理, 可以证明(id⊗((s+)*)-1)(F′⊗G′)是F⊗G的逆元.

所以,(id⊗((s+)*)-1)(F⊗G)=(id⊗((s+)*)-1)(F′⊗G′)也是F⊗G的逆元.根据逆元的唯一性，得到

进一步，有

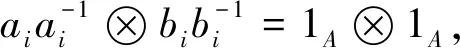
再由(3)，可得

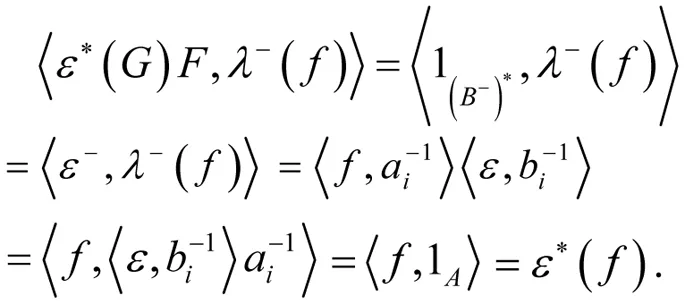
引理2 ∀f,g∈A°，有〈F⊗G,ρ+(f)⊗

λ+(g)〉=〈f,ai〉〈g,bi〉.

证明因为ρ+=s-∘λ-，所以ρ+(f)=s-∘λ-(f). 直接计算，得到

定理2 Hopf代数B-与((B+)*)cop同构.

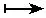
下面证明ψ:B-→((B+)*)cop是Hopf代数同构映射.

由命题2可知，λ±是反代数同态和余代数同态，则

因此ψ(λ-(f)λ-(f′))=ψ(λ-(f))*

ψ(λ-(f′))，即ψ是代数同态. 再注意到因此，ψ(λ-(f1)⊗λ-(f2))=Δτ(ψ(λ-(f)))，即ψ是余代数同态.

下面证明ψ既是单射又是满射. 设

ψ(λ-(f))=ψ(λ-(f′))，则∀g∈A°,〈ψ(λ-1(f)),λ+(g)〉=〈ψ(λ-(f′)),λ+(g)〉,

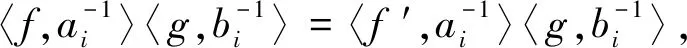
s-(λ-(f))=λ-(f′),(s+)-1(λ+(g))=λ+(g′),根据ψ的定义，直接得到

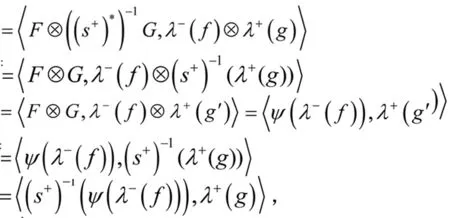
由λ+(g)∈B+的任意性，得ψ(s-(λ-(f)))=(s+)-1(ψ(λ-(f))). 再由λ-(g)∈B-的任意性，有ψ∘s-=(s+)-1∘ψ. 综上所述，ψ是Hopf代数同构映射，作为Hopf代数，B-与((B+)*)cop同构.