，，

(1.北京科技大学 自动化学院，北京 100083; 2.北京科技大学 计算机与通信工程学院，北京 100083)

依据列相关性优化高斯测量矩阵

边胜琴1，2，徐正光1，张利欣1

(1.北京科技大学自动化学院，北京100083; 2.北京科技大学计算机与通信工程学院，北京100083)

为了提高信号重建的精度以及稀疏度适用范围，提出了一种新的测量矩阵优化方法，减小测量矩阵和稀疏变换矩阵的相关性;首先，由测量矩阵和稀疏变换矩阵的乘积构造Gram矩阵；根据Gram矩阵的维数，计算互相关函数的下确界即Welch界；其次，由Welch界确定阈值，收缩Gram矩阵中大于阈值的非对角元；然后，由新得的Gram矩阵和稀疏变换矩阵反解出测量矩阵，迭代更新，从而达到减小相关性，优化测量矩阵的目的;实验结果表明：依据Welch界优化测量矩阵，能快速降低压缩感知矩阵相关性的最大值，提高OMP算法的性能，例如在误差率为10-0.9时，原高斯随机矩阵需要23个观测值，算法优化后只需16个观测值，相对于Elad、Zhao等观测矩阵优化方法，文中提出的算法具有更小的重构误差，性能和稳定性也略有提升。

压缩感知；测量矩阵；互相关系数；信号重构

0 引言

2004年由Donoho[1]、Candès[2-3]、及华裔科学家Tao(陶哲轩)等人提出的压缩感知理论(compressive sensing，CS)，突破了传统的奈奎斯特采样定理的限制，实现了数据的获取和压缩同时进行，避免了对大量无用信息地采集，降低了数据存储、传输和处理的开销，在信号处理领域产生了极其重要的影响，引起了众多科学家的关注。目前，在医学成像、生物传感、遥感成像、图像处理等领域，应用也越来越广泛。

信号的稀疏表示是压缩感知的前提，研究人员发现根据信号的特征，总可以找到它稀疏表示形式。压缩感知理论对信号进行稀疏表示之后，再通过一个测量矩阵，将其投影到一个低维空间，通过低维观测值对原始信号进行重构。

1 测量矩阵

测量矩阵的性能和信号的稀疏度范围密切相关，如何设计或者优化测量矩阵，减少测量次数或者增大信号的稀疏度范围，成为压缩感知理论的一个重要方向[4-5]。现有文献对此展开研究，主要有约束等距性质(restricted isometry property，RIP)，零空间性质和互相关系数[6-13]等。文献[6]提出了约束等距性质，并指出约束等距性是信号能够完全重构的充分条件。零空间性质是指同一个测量值通过l1范数优化得到的解具有唯一性。判定观测矩阵是否具备RIP性质和零空间性质，需要遍历多个子集，计算复杂度高，用来指导测量矩阵的构造不太现实。很多学者尝试用相关性理论[9-10]，来衡量测量矩阵的性能，弱化RIP条件。研究表明，减小测量矩阵与稀疏变换矩阵的互相关系数，能够提高压缩感知算法的重构性能，互相关系数越小，信号精确重建所需的测量次数就越少，信号适用的稀疏度范围就越大[11]。

感知矩阵优化的基本思想是：保持稀疏变换矩阵不变，只对测量矩阵进行优化，先通过测量矩阵和稀疏变换矩阵的乘积构造格拉姆(Gram)矩阵，在迭代过程中减少格拉姆矩阵的非对角元的绝对值，由新得的格拉姆矩阵和原稀疏变换矩阵更新测量矩阵。Elad[7]提出了一种阈值平均系数法，通过线性收缩Gram矩阵中绝对值大于阈值的非对角元，减小平均互相关系数，从而优化传感矩阵，但收缩因子和阈值点配置依靠经验，参数不当，可能需要较多的迭代次数；Vahid[12]采用梯度下降法使Gram矩阵接近单位矩阵，但是，压缩感知中的Gram矩阵不是满秩矩阵，和满秩的单位矩阵只能近似；文献[8]定义了一种整体互相关系数，在不改变Gram矩阵的迹也即特征值之和的前提下，平均化所有非零特征值，使得非对角元整体平方和最小的方式优化观测矩阵，实验表明，采用这种方式优化，相关系数下降较快，但是容易达到局部最小值。文献[13-15]提出了等角紧框架理论(Equiangular Tight Frame，ETF)，并给出矩阵列相关性的边界，边界最小值也即下确界称为Welch界，采用构造方法生成的矩阵才具有边界最小值。

本文对测量矩阵优化方法进行了研究，提出了一种新的优化方法，减小Gram矩阵中较大的非对角元，经过较少的迭代次数，就能将Gram矩阵的相关系数降到Welch界附近；在相同迭代次数的情况下，与文献[7-8]中的方法相比，最大相关性和平均相关性，都较低，从而在信号重构时，能够提高信号的重构精度，降低压缩感知系统对信号稀疏度的要求。

2 基本原理

2.1 压缩感知理论

长度为N的信号x∈N，在给定的一组标准正交基Ψ=[Ψ1,Ψ2,…,ΨN]上表示为：

或x=Ψα

(1)

若N×1维的列向量α中只有K(K≼N)个非零系数，则称信号x在基矩阵Ψ下是K稀疏的。若非零系数排序后，按指数级衰减趋于零，则称信号是可压缩的。

压缩感知的过程是：长度为N的信号x，通过测量矩阵Φ∈M×N进行投影，得到观测值y∈M(M≼N)，再由观测值y对信号进行精确重构。

观测过程表示为：

y=Φx

(2)

将稀疏表示(1)代入(2)式，得:

y=Φx=ΦΨα=Αα

(3)

Φ∈M×N称为测量矩阵或投影矩阵，Ψ∈N×N称为稀疏矩阵，Α=ΦΨ，Α∈M×N称为感知矩阵。

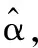
当原始信号x本身就是K稀疏的信号时，稀疏变换矩阵Ψ是单位矩阵，测量矩阵Φ满足一定条件，信号x就可以通过最小l0范数优化问题精确重构。

s.t.y=Φx

(4)

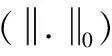
求解(4)式，一种方法是采用匹配追踪类算法，通过每次选取局部最优解来逐步逼近原始信号，由于复杂度低，获得广泛应用，主要算法包括匹配追踪(matching pursuit，MP)、正交匹配追踪(orthogonal matching pursuit，OMP)、分级正交匹配追踪(stagewise orthogonal matching pursuit，StOMP)、正则化的正交匹配追踪(regularized orthogonal matching pursuit，ROMP)、子空间追踪(subspace pursuit，SP)、压缩采样匹配追踪(compressive sampling matching pursuit, CoSaMP)等。另外一种方法是将最小l0范数转化为最小l1范数问题，采用凸优化方法求解，主要包括基追踪法(basic pursuit，BP)，欠定系统局部解法(focal underdetermined system solver，FOCUSS)，梯度投影重建法(gradient projection for sparse reconstruction，GPSR)等。凸优化方法在测量矩阵满足限制等容条件下，能够精确重建所有的稀疏信号，而且所需的测量次数也较小，但是计算复杂度高，对于大尺度问题，计算时间长，不太实用。

对于测量矩阵Φ来说，列数始终大于行数，列数越小，说明对采样率的要求就越低，并且要求Φ和Ψ不相干，Φ的行向量不能由Ψ的列向量进行稀疏表示。高斯随机矩阵、贝努利随机矩阵、部分傅里叶随机矩阵及稀疏投影矩阵等，几乎与所有的稀疏基都不相关，可以作为普适性的观测矩阵。但是文献[14]指出，测量矩阵和稀疏字典对应的Gram矩阵并没有逼近理想模型，信号的重构精度和稀疏度范围还有可以提升的空间。

2.2 Gram矩阵和互相关系数

定义1(相关性)：矩阵A的互相关系数，也即A的相干性，是矩阵A的任意两列的内积最大值。

其中:ai和aj都是矩阵Α的列向量。

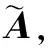
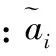
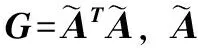
由定理2可以看出，互相关系数和信号的稀疏度成反比例关系，互相关系数越小，精确重构信号的稀疏度范围就越大，反之，互相关系数越大，精确重构信号的稀疏度范围就越小，对维数确定的观测矩阵来说，所需的观测值数目相对较大。定理1表明Welch界是相关系数的下确界，只有任意两列内积都相等时，才能达到，对于高斯随机矩阵来说，不可能达到最小值，但是可以将Welch界作为调整Gram矩阵的一个重要参数，对观测矩阵进行优化。

2.3 依据Welch界优化观测矩阵

观测矩阵优化的具体过程是：首先，由测量矩阵和稀疏变换矩阵的乘积，计算Gram矩阵及其相关性的下确界(Welch界)，并将2倍Welch界作为优化算法的阈值；其次，缩小Gram矩阵中大于阈值的非对角元，缩小到原来的一半，保留小于阈值的元素；再者，对修改后的Gram矩阵进行奇异值(singular value decomposition，SVD)分解，保证奇异值个数不变，将Gram矩阵的秩收缩，再由Gram矩阵和稀疏字典计算出测量矩阵；反复迭代，当Gram矩阵中不存在大于2倍Welch界的非对角元时，调整阈值，对较大的非对角元进行微调，重复上述过程，直到完成迭代次数。

整体算法步骤如下：

1)初始化高斯随机矩阵Φ∈M×N，Φ为列满秩矩阵，选择稀疏矩阵为Ψ∈N×N，感知压缩矩阵Α=ΦΨ，Α的维数为M×N，迭代次数t=1；

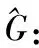
如果Gram矩阵非对角线上的元素都小于给的的阈值，按下式修改G的非对角元，

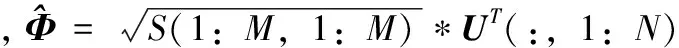
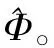
3 实验结果

3.1 优化前后Gram矩阵比较

构造50*120的高斯随机矩阵作为测量矩阵，采用绝对稀疏的随机信号作为重建对象，稀疏矩阵即为单位矩阵，测量矩阵和稀疏矩阵之间的相关性按定理1计算，则最小互相关系数也就是Welch界为：W(Α)=0.1085，采用上述方法对矩阵进行优化，大于阈值的元素缩小到原来的0.5倍，小于阈值的元素保持不变，迭代30次，大于阈值的元素不存在时，将绝对值最大的非对角元的0.9倍作为新的阈值，继续迭代，直到达到设定的迭代次数。结果如图1所示，(a)为原始高斯的矩阵的Gram矩阵，(b)为训练后测量矩阵的Gram矩阵，(c)为训练后测量矩阵的Gram矩阵的绝对值；参照色彩条状轴，比较图(a)(c)可知，Gram矩阵非对角元素的值在逐渐减小，而且十分接近，说明优化后矩阵相干性绝对值缩小了，而且范围比较优化前要集中，这对信号重构十分有用。

图1 Gram矩阵比较

3.2 观测矩阵优化前后直方图比较

测量矩阵和稀疏字典的乘积Gram矩阵共有14 400个元素，除去对角线全1的元素还剩14 280个元素，采用上述方法对矩阵进行优化，将非对角元素的绝对值分成80组，对Gram矩阵非对角元的分布状况进行分析，如图2所示。

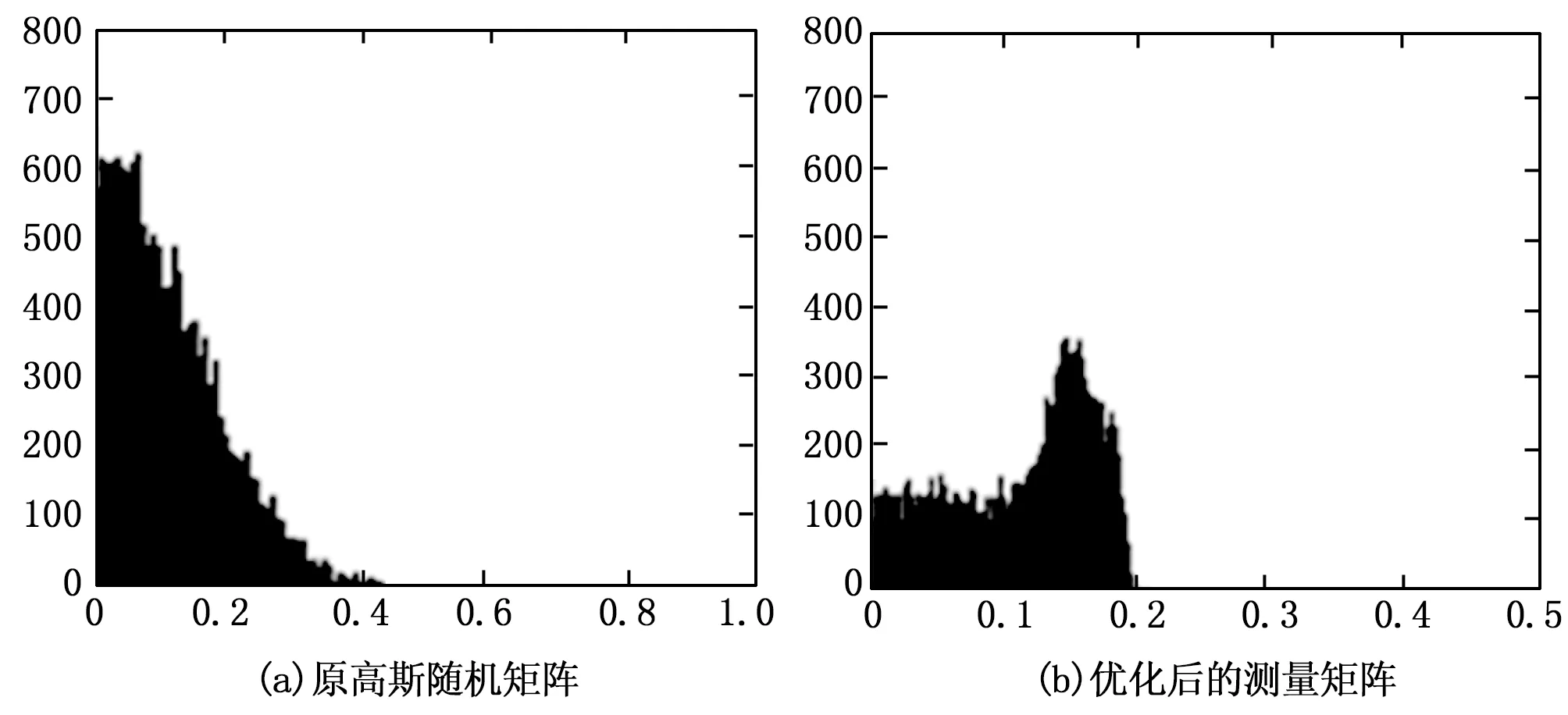
图2 Gram矩阵非对角元绝对值的直方图

横坐标表示Gram矩阵的非对角元的绝对值，纵坐标表示相应区间的元素的个数，可以看出，优化前在0附近的元素最多，相关性最大值为0.61；迭代100次后在0.16附近的元素最多，相关性最大值缩小到0.2，元素的分布更加密集，说明本文提出的方法确实能够降低观测矩阵的相关性，使得相关性分布在Welch值附近。对Gram矩阵采用不同方法优化后，最大相关性和平均相关性也不同，对上述矩阵迭代9次进行比较，最大相关性即乘积矩阵中的非对角线元素的最大值，平均相关性是乘积矩阵中前20个较大的非对角元的均值，由表1可以看出，在前9次的迭代运算中，本文方法得到的最大相关性和平均相关性均小于由文献[7]和文献[8]得到的值；比较前30次的迭代，本文方法得到的平均相关性始终最低。

3.3 OMP和BP算法优化前后比较

为了验证观测矩阵优化算法在整个压缩过程中的有效性，本文进行了两次实验。

实验一：选取50 000个向量，向量长度为120，每个稀疏向量包含4个非零项，非零项的位置随机分布，进行压缩感知实验，观测次数的取值范围为[16,32]，分别BP算法和OMP算法对观测信号进行重构，测试重构误差随观测次数的变化，检验投影矩阵的性能。

表1 相关性比较

分别采用4种不同观测矩阵进行比较，原高斯随机矩阵，文献[7]优化方法、文献[8]优化方法，以及本文优化方法，当重构错误次数大于200时，迭代终止，前200次的平均误差作为以后的重构误差。实验结果如下图所示，横坐标为测量次数，纵坐标为重构误差的对数表示，实验部分代码来自SparseLab实验箱。

由图3(a)可以看出，优化投影矩阵能大幅提高OMP算法的性能，例如在10-0.9的重构误差下，原高斯矩阵需要23个观测值，而文献[7]和本文方法优化的观测矩阵只需要16个，说明观测矩阵优化后，每个观测值包含更多的信息量，投影矩阵的优化，能够提升信号的重构性能。图3(b)表示BP算法在观测矩阵优化下信号重构性能略有提升，4种观测矩阵重构误差相差不是很大。两个图的共同点是随着观测次数的增加，重构误差率在逐渐减小，相对于其他3种测量矩阵，文中提出的优化算法，具有更小的重构误差率。

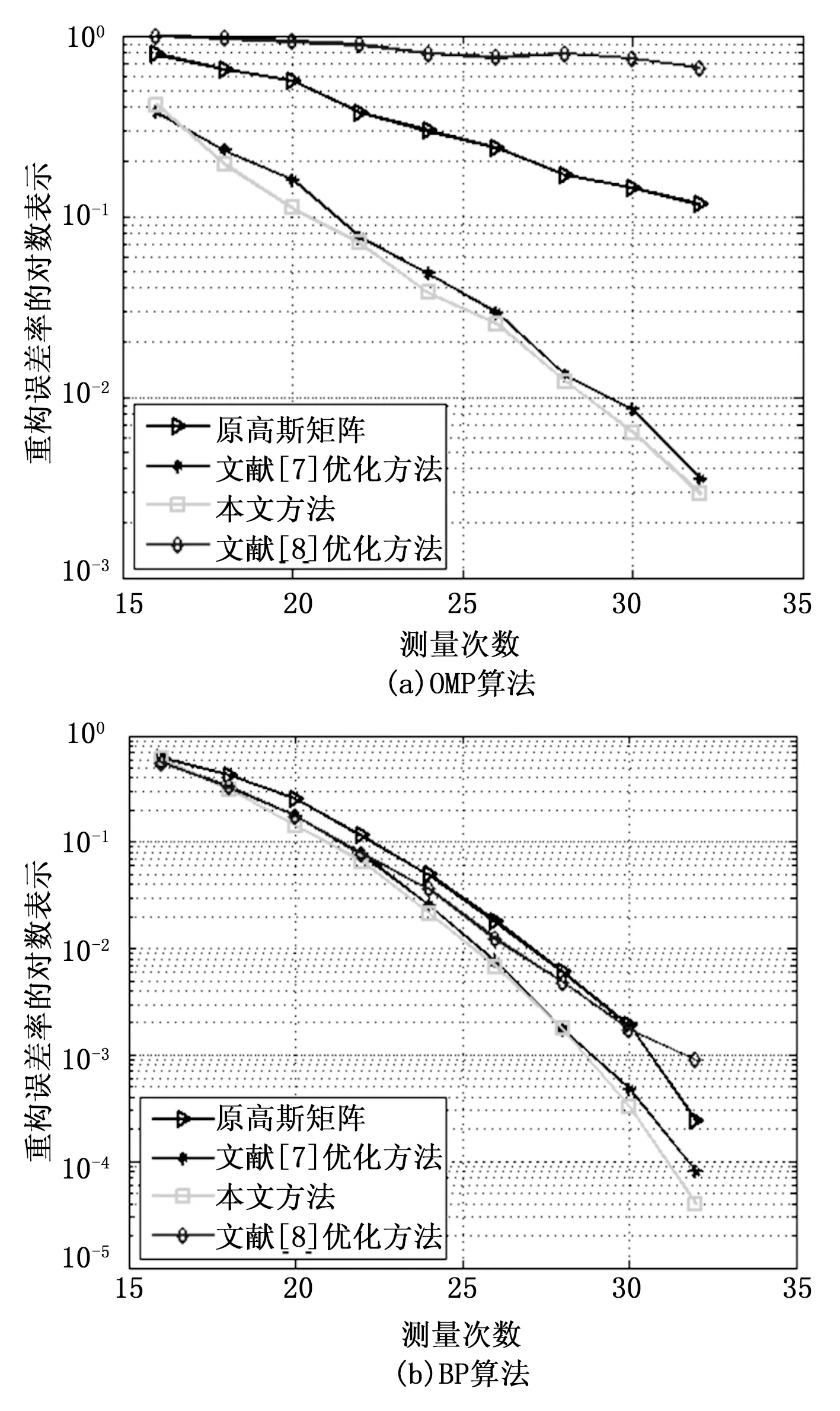
图3 不同优化算法随观测次数m的变化

实验二：同样选取50 000个向量，向量长度为120，固定观测次数为25次，向量的稀疏度从3逐渐增加到9，测试重构误差随稀疏度的变化，检验投影矩阵的性能。

原始投影矩阵为25×80的高斯随机矩阵，对以上4种优化算法进行仿真，当重构错误次数大于200时，迭代终止，前200次的平均误差作为以后的重构误差。横坐标为信号的稀疏度，纵坐标为重构误差的对数表示，结果如图4所示。

图4 不同优化算法随信号稀疏度K的变化

图4表明，随着信号稀疏度的增加，重构误差率在逐渐增大，观测矩阵优化后，文献[7] 和本文方法比原高斯随机矩阵，采用OMP算法重构时，具有更小的重构误差，文献[8]提出的优化方法在本文的实验条件下，性能不及原高斯随机矩阵。使用BP算法重构时，重构误差随着稀疏度的增加，差异性越来越小，本文优化方法略优于其他算法。

4 结论

本文提出了一种优化测量矩阵算法，由测量矩阵和稀疏变换矩阵的乘积得出Gram矩阵，Gram矩阵的非对角元即测量矩阵的行向量与稀疏变换矩阵的列向量的相关性，根据代数中的定理可知，满秩矩阵列向量之间的相关性存在最小值，称为Welch界。将Gram矩阵的Welch界作为优化测量矩阵的目标，缩小Gram矩阵的非对角元；再对调整后的Gram矩阵进行奇异值分解，保证奇异值的个数不变，反解出新的测量矩阵；重复上述过程，直到达到设定的迭代次数。实验证明，Gram矩阵的相关性能快速地下降到Welch界附近，由此得到的测量矩阵，在进行图像重建时，压缩感知性能和重建质量都有不同程度的提高。

[1] Donoho D L, Elad M, Temlyakov V N. Stable recovery of sparse overcomplete representations in the presence of noise[J]. IEEE Transactions on information theory, 2006, 52(1): 6-18.

[2] Candes EJ, Romberg J K, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transaction on Information Theory, 2006, 52(2): 489-509.

[3] Candes E J, Romberg J K, Tao T. Stable signal recovery from incomplete and inaccurate measurements [J]. Communications on pure and applied mathematics, 2006, 59(8): 1207-1223.

[4] 郑 红, 李 振. 压缩感知理论投影矩阵优化方法综述 [J]. 数据采集与处理, 2014(1): 43-53.

[5] 戴琼海，付长军，季向阳. 压缩感知研究 [J]. 计算机学报, 2011, 34(3): 425-434.

[6] Candes E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9-10): 589-592.

[7] Elad M. Optimized projections for compressed sensing[J]. IEEE Transactions on Signal Processing, 2007, 55(12): 5695-5702.

[8] 赵瑞珍，秦 周，胡绍海. 一种基于特征值分解的测量矩阵优化方法 [J]. 信号处理, 2012, 28(5): 653-658.

[9] Baraniuk R, Davenport M, DeVore R, et al. A simple proof of the restricted isometry property for random matrices [J]. Constructive Approximation, 2008, 28(3): 253-263.

[10] Xu J, Pi Y, Cao Z. Optimized projection matrix for compressive sensing[J]. EURASIP Journal on Advances in Signal Processing, 2010, 2010(1): 560349.

[11] Donoho D L, Elad M. optimally sparse representation in general(non-orthogonal)dictionaries via minimization [J]. Proceeding of the National Academy of Sciences, 2003, 100(5): 2197-2202.

[12] Abolghasemi V, Ferdowsi S, Sanei S. A gradient-based alternating minimization approach for optimization of the measurement matrix in compressive sensing [J]. Signal Processing, 2012, 92(4): 999-1009.

[13] Tropp J A, Dhillon I S, Heath R W, et al. Designing structured tight frames via an alternating projection method [J]. IEEE Transactions on information theory, 2005, 51(1): 188-209.

[14] Strohmer T, Heath R W. Grassmannian frames with applications to coding and communication [J]. Applied and computational harmonic analysis, 2003, 14(3): 257-275.

[15] Sustik M A, Tropp J A, Dhillon I S, et al. On the existence of equiangular tight frames [J]. Linear Algebra and its applications, 2007, 426(2-3): 619-635.

[16] Tillmann A M, Pfetsch M E. The Computational Complexity of the Restricted Isometry Property, the Nullspace Property, and Related Concepts in Compressed Sensing [J]. IEEE Transactions on Information Theory, 2014, 60(2): 1248-1259.

[17] 吴光文，张爱军，王昌明. 一种用于压缩感知理论的投影矩阵优化算法 [J]. 电子与信息学报, 2015(7): 1681-1687.

[18] 李哲涛，潘 田，朱更明,等. 低幂平均列相关性测量矩阵构造算法 [J]. 电子学报, 2014(7): 1360-1364.

[19] 柯家龙，李继楼. 压缩感知中的投影矩阵优化算法 [J]. 计算机技术与发展, 2015(3): 95-98.

OptimizeMeasurementofGaussianMatrixBasedonColumnCorrelation

Bian Shengqin1，2, Xu Zhengguang1, Zhang Lixin1

(1.School of Automation and Electrical Engineering, Beijing University of Science and Technology, Beijing 100083, China；2.School of Computer and Communication Engineering, Beijing University of Science and Technology, Beijing 100083, China)

In order to improve the accuracy of signal reconstruction and the application range of sparsity, a new method of measuring matrix optimization is proposed. First, multiply measurement matrix and sparse transformation matrix to construct a Gram matrix, and calculate the minimum value of mutual coherence, that is the Welch bound; Secondly, set a threshold based on Welch bound and reduce the elements of the non-diagonal of the Gram matrix; Third, produce new projection matrix from inverse solution of new Gram matrix and sparse transformation matrix iteratively, so as to achieve the purpose of reduction the mutual coherence and optimizing the measurement matrix. Experiments in the last show: measurement matrix based on the Welch optimization can rapidly reduce the maximum value of the compressed sensing correlation matrix and improve the performance of OMP algorithm, such as when error rate is 10-0.9, the original Gauss random matrix need 23 observations, but our optimized matrix only 16 observations. On the whole, when compared with the optimization method of Elad and Zhao, the reconstruction error of the algorithm in this paper is smaller, the performance and stability are slightly improved.

compressive sensing(CS); projection matrix; mutual coherence; signal reconstruction

2017-04-12；

2017-05-08。

边胜琴(1977-)，女，河北保定人，博士研究生，主要从事压缩感知方向的研究。

徐正光(1952-)，男，教授，博士研究生导师，主要从事控制科学与工程、图像处理方向的研究。

1671-4598(2017)11-0141-05

10.16526/j.cnki.11-4762/tp.2017.11.036

TP911.7.1

A