张启新

(华南师范大学 数学科学学院, 广州 510631)

一个组合公式的证明及在取球问题中的应用与推广

张启新

(华南师范大学 数学科学学院, 广州 510631)

本文研究了一种不放回的取球问题, 导出了与该问题密切相关的组合公式, 在对公式进行研究后加以推广, 并将推广的结果应用到了更广义的取球问题中.

取球问题; 数学期望; 组合数学; 组合公式

一、公式导出与求解

本文先探究如下的取球问题:

例1 在一个黑箱中放入2n个除颜色外无任何区别的小球, 其中有n个黑球和n个红球. 现从黑箱中取球, 规则如下: 若取出的是黑球, 则不放回地继续取球; 若取出的是红球, 则停止取球. 设取出黑球的数量为X, 求X的数学期望

注1 为了后续的表述方便, 该问题称为n×n的连续取球问题.

解易知X=0,1,2,…,n, 且

⋮

一般地, 有

所以取到的黑球数的期望为

因此, 例1转化成了求解该组合式:

为了求解上述组合式, 首先需要如下引理.

该结论是显然的, 事实上该式右端只是将左端求和符号内每一项的下标进行倒序重排.

我们有下面的结论.

(1)

证明上式等价于

为此, 只需证明

(2).

将(2)式左端改写成

利用引理1, 还可改写为

(3)

上面的步骤将(1)式变化成了(3)式, 我们将证明之.

设fn(k)=(n-k+1)(n+k-2)!k(k+1)…(n+1),

那么(3)式又进一步化成了

Sn(n)=(2n)!

(4)

代入前几项的值, 可算得

Sn(1)=n!(n+1)!;

Sn(2)=n!(n+1)!+(n-1)n!(n+1)!=nn!(n+1)!;

据此观察猜想

(5)

(5)式对k=1,2,3,4均成立. 假设结论对k≤s(s为正整数)均成立, 对于k=s+1, 有

Sn(k)=Sn(s+1)

=Sn(s)+fn(s+1)

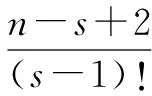
所以(5)式对k=s+1也成立. 于是由数学归纳法可知, 对于一切正整数k(k≤n), (5)式均成立.

将k=n代入(5)式, 得到

=2n(2n-1)!=(2n)!.

所以(4)式成立, 由此知(1)～(3)式均成立, 证毕.

回到例1, 利用已有结论, 可得

定理1.2n×n的连续取球问题的取球数期望为

二、公式与问题的推广

例1的取球问题中, 红球和黑球的地位是对称的,因此, 定理1的组合公式的应用范围也仅限于两种球数量相等的情形, 为此考虑将例1的取球问题推广到非对称的情形, 即下面的例2.

例2 在一个黑箱中放入n+m个除颜色外无任何区别的小球, 其中有n个黑球和m个红球. 现从黑箱中取球, 规则如下: 若取出的是黑球, 则不放回地继续取球; 若取出的是红球, 则停止取球. 设取出黑球的数量为X, 求X的数学期望.

注3 为后续表述方便, 称该问题为n×m的连续取球问题.

解易知X=0,1,2,…,n,且

⋮

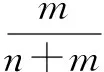
所以取到黑球的数学期望为

因此, 我们导出了一个组合式

易见该组合式是定理1中组合式的推广.

引理2 (二重数学归纳法)设有一个与两独立正整数m,n有关的命题p(m,n), 满足:

(1)p(m,1)与p(1,n)成立.

(2) 如果p(m,n+1)与p(m+1,n)均成立, 则p(m+1,n+1)也成立

那么该命题对一切正整数m,n均成立.

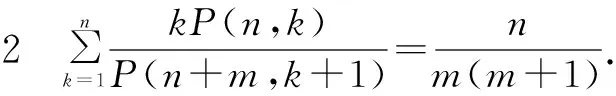
(6)

证明(6)式等价于

将求和式中的常数项提出来移到等式右边, 即有

利用引理1, 可化成

定理2转变为

(7)

所以(7)式对L(m,1)和L(1,n)成立.

如果(7)式对L(m,n+1)和L(m+1,n)成立, 则

=mL(m,n+1)+L(m+1,n)

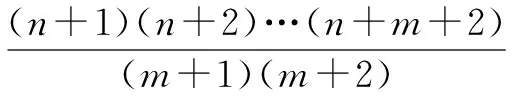
故(7)式对L(m+1,n+1)也成立, 由引理2知对所有正整数m,n, 均有

定理2证毕.

至此, 例2也得到了解决. 于是有下面的结论.

定理2.2n×m的连续取球问题的取球数期望为

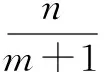
三、进一步推广

现在, 我们考虑

设其为A, 结合定理2, 有

利用该结果, 还可以有如下的

定理3n×m的连续取球问题的取球数方差为

证明由概率论的方差公式, 有

至此, 我们成功地将导出的组合公式做出了两种推广, 并将之用到了具有实际意义的组合问题中. 可见, 将一个问题抽象化为公式之后, 我们可以根据问题本身的特点将公式进行推广, 并将推广的结果应用到问题中去, 得出更多的结论.

[1] 熊斌, 田延彦. 国际数学奥林匹克研究[M]. 上海:上海教育出版社，2008：39-40.

[2] 盛骤等. 概率论与数理统计(第四版)[M]. 北京:高等教育出版社, 2008:100-101.

[责任编辑：杨惠民]

G632

A

1008-0333(2017)25-0029-03

2017-07-01

张启新(1996.3-)，男，汉，广东省广州人，在校学生.