张兴刚 戴丹

1)(贵州大学物理学院,贵阳 550025)

2)(贵州大学计算机科学与技术学院,贵阳 550025)

二维颗粒堆积中压力问题的格点系统模型∗

张兴刚1)†戴丹2)

1)(贵州大学物理学院,贵阳 550025)

2)(贵州大学计算机科学与技术学院,贵阳 550025)

粮仓效应,应力分布,格点系统,三对角矩阵

为了便于从理论上探究粮仓效应产生的机理,处理筒仓中颗粒介质的应力分布等问题,将二维颗粒堆积简化为格点系统,并且以随机堆积为物理背景提出了一个由吸收系数p及侧向传递系数q决定的力传递模型.给出了矩阵形式的力传递方程,提出基于二阶差分方程的方法同时求解传递系数矩阵的特征值和特征向量,从理论上导出了一种典型情况下容器底部压力分布与顶部压力分布的关系式.对有效质量随总质量变化关系的理论分析表明,该模型可以给出与Janssen模型类似的结果.对无负载情况下的底部应力分布进行了理论计算,结果表明容器底部中央应力最大,离中央越远应力越小.运用数值计算讨论了p与q对容器底部压力随堆积高度变化曲线的影响.

1 引 言

颗粒物质静力学主要研究静态颗粒体系的堆积结构、颗粒间的相互作用、颗粒介质中的应力分布等问题,在粮仓的设计、堆石坝的稳定性、地基的承载能力等工程问题中有直接应用,山崩、滑坡、塌陷等灾害的理解也与其密切相关.有许多有趣的颗粒物质静力学现象,例如粮仓效应和沙堆应力凹陷[1].人们很早就发现了粮仓效应,即粮仓底部所受压力随粮食堆积高度的增加趋于饱和的现象.早在1895年,德国工程师Janssen就提出了一个基于某些假设的连续介质模型,给出了粮仓效应的简单解释[1,2].在粮仓效应的相关实验中,通常关注容器底部测得的有效质量Me(即容器底部压力与重力加速度g的比值)与容器中颗粒总质量Mt的关系.根据Janssen模型可建立颗粒介质的力学平衡方程,在容器顶部无负载的情况下,可以求得有效质量为

式中Ms为饱和质量.(1)式对于二维和三维的情况都适用[3].在一定实验条件下,所得到的实验结果可以用Janssen模型予以解释.

然而,颗粒堆中的应力问题并不简单.一般情况下需要结合应力平衡方程∇·σ+ρg=0(其中σ为颗粒介质的应力张量场,ρ为介质的密度分布)、介质的本构关系、边界条件等因素,才能从理论上确定介质中的应力分布.但是,目前还没有普遍适用的关于静态颗粒介质的本构关系,实际颗粒堆中的边界条件也往往难以确定;更为困难的是,颗粒介质的宏观性质往往与其制备方式、加载条件等因素密切相关.事实上,颗粒物质静力学中有许多基本的物理问题需要深入研究[4].直到最近,仍有不少关于粮仓效应、Janssen模型等经典问题的研究报道,人们从实验[3,5−10]、计算机模拟[11]、理论模型等[3,12−14]方面对筒仓中颗粒堆的压力问题进行了更深入的探讨.在大部分研究工作中,容器底部所受压力随颗粒堆积高度的变化(可间接用Me(Mt)函数表征)仍是一个基本问题.不过,人们用不同的方式、从不同的角度加深了对这一问题的认识.Vanel等[3]发现顶部负载较大时,Me(Mt)会呈现非单调变化,这与Janssen模型预言的单调变化不相符,用OSL(oriented stress linearity)模型可比较好地理解这一现象.Wambaugh等[7]用光弹性实验对不同顶部负载下的Me(Mt)关系进行研究,观察到了非单调变化、Me没有趋向饱和、Janssen模型中的特征长度并非常数等现象.另外,研究者通过匀速移动筒仓侧壁[5]、上提或下压侧壁等[6,14]方式改变实验条件,研究了Me(Mt)关系、颗粒对侧壁的最大静摩擦力等问题.最近,有人提出新的实验方法测量颗粒对侧壁的作用力[9,10],例如文献[9]中通过图像关联技术测量弹性容器壁的应变场,从而间接测量侧壁所受的应力分布.

颗粒体系的宏观力学性质应该由其微观结构、相互作用的统计特征决定.两个宏观上看起来相同的颗粒堆,它们的微观状态一般不同,其中重要微观因素的不同有可能导致宏观上力学性质的重大差异.前人的研究表明,对于同样的问题,不同的实验过程往往会得到不同的实验结果[5−10];另外,已有宏观理论模型只在一定条件下可以用于理解部分实验结果,目前不是很清楚这些模型适用(或者不适用)的物理机理.可以看到,这些问题主要来源于颗粒体系在微观结构和相互作用方面的多样性、不确定性、易变性,以及尚不明确的体系的微观特征与宏观力学性质之间的关系.因此,加强对微观结构、力网、力传递等问题的研究,建立微观特征与宏观性质之间的联系,对于颗粒静力学来说非常重要[4,15].文献[13]建立了圆盘的晶格堆积模型,基于力学平衡条件得到了相邻两层颗粒间力传递的规则,并且利用力传递规则给出了容器底部总压力会随着堆积层数增加趋向饱和的结果.实际的颗粒堆一般是非晶格结构,难以直接从微观上对其进行理论研究,且更细致的研究应该讨论应力分布,而不只是总的压力.标量q模型[16,17]将颗粒堆积抽象为格点系统,通过上下两层格点间重量的随机传递简化实际堆积中颗粒间的相互作用;结合马尔科夫过程理论,q模型可以比较好地用于理解随机堆积中力的概率分布等问题.

受到q模型的启发,为了便于从理论上探究顶部压力分布与底部压力分布之间的关系,本文将二维颗粒体系简化、抽象为带有边界的格点系统,以随机堆积为物理背景建立了一个由p和q这两个参数决定的力传递模型,其中吸收系数p反映了边界由于摩擦而对颗粒产生的支撑作用,侧向传递系数q描述了颗粒向其正下方左右两侧传递力的能力.该模型的解析计算涉及到一种三对角矩阵的相似对角化,我们提出基于二阶差分方程的方法同时求解三对角矩阵的特征值和特征向量,对p=1/2,q=1这一典型的情况进行了解析计算.最后,通过模型的求解讨论了Me(Mt)关系、底部压力分布等问题.该研究加深了对微观力传递规则与宏观压力分布之间关系的认识.

2 格点系统模型

为了研究筒仓中颗粒物质对容器底部产生的总压力以及压力的分布,可以考虑图1所示二维颗粒体系.如果颗粒的尺寸远小于容器的尺寸,则可以将容器中的颗粒体系看作连续的颗粒介质.对于二维的情况,颗粒介质的密度可以用ρ=Mt/(LxLy)表征,其中Mt为颗粒介质的总质量;边界处压力的分布可以用应力(即单位长度边界所受的压力)的分布表征.于是颗粒介质顶部所受的负载可用应力函数σ(x,0)描述,容器底部的应力分布可用函数σ(x,Ly)描述.二维颗粒堆积中关于压力分布的一个基本问题,是根据σ(x,0)以及颗粒体系的一些特征求出σ(x,Ly).实际的静态颗粒体系往往是非晶格的堆积,很难从微观上对其进行细致的几何和力学分析.为了避免直接分析堆积结构带来的困难,将二维颗粒堆积简化为图2所示的规则排列格点系统.在格点系统中,一个格点等效于一小团颗粒,第m行第n列的格点可用符号P(m,n)表示,设每个格点的质量均为m0,则每个格点都会受到重力m0g的作用.记竖直方向上相邻格点的间距为Δy,水平方向上的间距为Δx,则

一般情况下,不能简单地使用力传递的概念理解物理问题,除非这一概念有力学规律的支撑.已有的研究表明[12,13,16,17],在一定条件下可以采用力传递这种简单、直观的方式处理静态颗粒体系中的许多力学问题,但应该注意的是,不同的微观结构往往会导致不同的力传递规则.类似于标量q模型,以随机堆积为物理背景,定义格点系统中一种典型的力传递规则,其大致情况如图2所示.规定同一行的格点间没有竖直方向的分力,不相邻的两行格点间也没有相互作用.对于任意格点P(m,n)

而言,称其所受的重力、顶部对其产生的载荷以及第m−1行格点(如果存在的话)对其产生的作用力为输入力,将P(m,n)对第m+1行格点及其对容器的作用力称为输出力.对于每一个格点,只有上述5种竖直方向分力的存在,为了保证格点在竖直方向的力平衡条件,总输入力必须等于总输出力.

1)当m=M时,格点只向容器底部输出力,有fM=wM;

2)当m/=M,n/∈{1,N}时,P(m,n)将其总输入力的q/2输出给P(m+1,n−1),将总输入力的q/2输出给P(m+1,n+1),剩下的(1−q)wmn输出给P(m+1,n),称q为侧向传递系数,满足0＜q≤1;

3)当m/=M,n∈{1,N}时,P(m,1)将其总输入力的(1−p)q输出给P(m+1,2),将总输入力的(1−p)(1−q)输出给P(m+1,1),剩下的pwm1输出给容器左侧,称p为吸收系数,满足0≤p＜1,P(m,N)的力传递情况与P(m,1)类似.

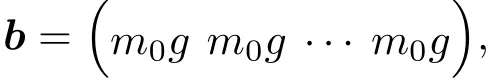
根据上述定义的力传递规则,当1≤m≤M−1时有力传递方程

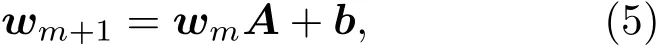
其中N阶方阵

称为传递系数矩阵,这是一个三对角矩阵[18].矩阵中的吸收系数p反映了容器侧壁与颗粒之间的摩擦所导致的格点总输入力被器壁吸收的程度,若容器侧壁与颗粒无摩擦,则p=0,有摩擦时0＜p＜1.矩阵中的侧向传递系数q反映了颗粒微团向其左右两侧传递力的程度,主要由微观的堆积结构决定,若颗粒微团只会向其正下方传递力,则q=0,但是这种情况在随机堆积中一般不存在.为表述方便,将该模型称为pq模型.为了由(4)式和(5)式推出wM,作变换可以得到

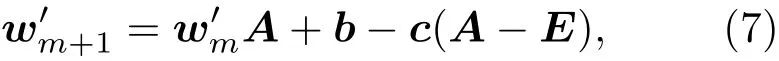
式中E为N阶单位矩阵.假设

则容易推出

假设A相似于对角矩阵Λ,即存在可逆矩阵Q使A=QΛQ−1,并且假设矩阵A−E可逆,那么结合(4)式、(8)式和(9)式可以得到

于是计算fM(即wM)相当于考虑传递系数矩阵A的相似对角化以及线性方程组(8)式的求解(或者矩阵A−E的可逆性).

3 传递系数矩阵的相似对角化

着重考虑N阶传递系数矩阵A的相似对角化问题.在p和q取一般数值的情况下,通过繁杂的数学讨论可以看到:矩阵A(p,q)的相似对角化本质上涉及到非特殊的高次代数方程的求解,无法找到其解析的结果.因此,以特殊但在物理上属于典型的p=1/2,q=1的情形进行理论分析,这相当于筒仓系统中颗粒与器壁的摩擦不是很小也不是很大,并且颗粒团由于成拱效应明显而几乎不向其正下方传递力的情况.此时矩阵A(1/2,1)是一个对称的三对角矩阵,根据线性代数中对称矩阵的相似对角化理论易知,存在N阶正交矩阵以及实对角矩阵Λ=diag(λ1,λ2,···,λN)使得

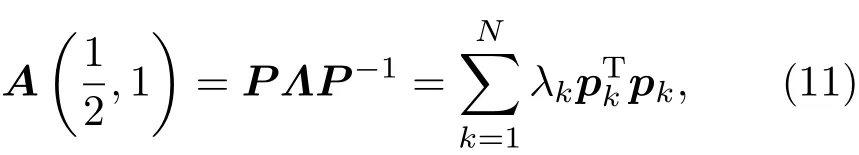
式中λk为A(1/2,1)的特征值,pNk)T为与λk相对应的单位特征向量.

为了给出矩阵P与Λ,需要考虑A(1/2,1)的特征值与特征向量.设xT=(x1,x2,···,xN)T是A(1/2,1)的特征向量,λ是相应的特征值,则

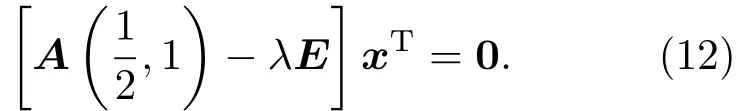
传统的线性代数理论是先由行列式给出矩阵的特征多项式,利用其对应的特征方程求解特征值,然后将特征值代入(12)式计算出相应的特征向量.这里采用直接分析齐次线性方程组(12)式的方法,同时进行特征值与特征向量的计算从而简化理论分析过程.将A(1/2,1)的矩阵形式代入(12)式可得带有边值条件的差分方程为

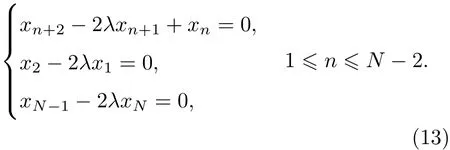
由于A(1/2,1)是实对称矩阵,其特征值都是实数,因此只需在λ∈R的范围内讨论(13)式.首先,根据二阶常系数差分方程理论求(13)式中差分方程的通解.该差分方程对应的特征方程为

以x1和x2为边值,则(15)式中的待定系数c1与c2应该满足

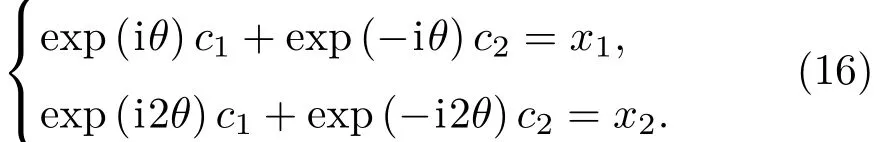
由θ/=k0π易知该方程组中系数矩阵的行列式不为零,容易得到向量(c1,c2)T的惟一解,将其解代入(15)式有

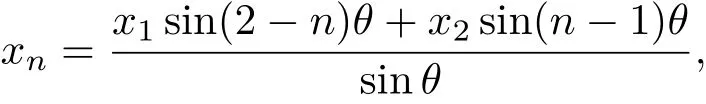
利用(17)式可得xN−1,xN关于x1,x2的表达式,将它们代入(13)式中的边值条件有

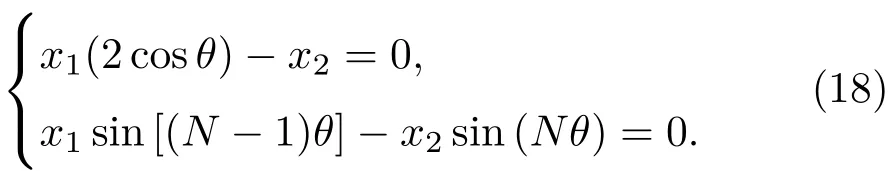
该方程组的系数矩阵行列式可化简为

由上述分析过程可知,|λ|＜1时矩阵A(1/2,1)的特征值由方程det(θ,N)=0中θ的解的情况决定.显然,当且仅当时det(θ,N)=0,其中结合θ/=k0π,λ=cosθ以及cosθ函数的基本性质可以得到A(1/2,1)的N个不同的特征值

这也是A(1/2,1)的所有特征值.因此p=1/2,q=1的情况下不用讨论λ=±1,|λ|＞1的情形.结合(17)式和(18)式可得与λk相对应的一个特征向量

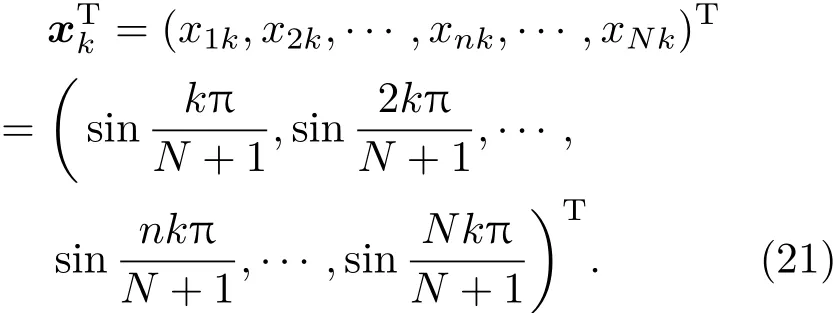
利用欧拉公式及等比数列求和不难求出的长度的平方

于是得到N个满足正交归一条件的特征向量

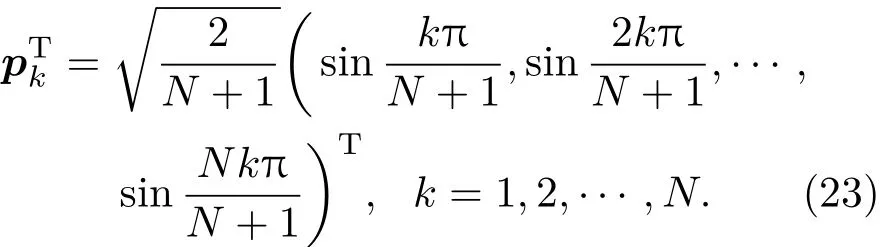
利用(20)式和(23)式可以给出(11)式中的矩阵P与Λ.至此,矩阵A(1/2,1)的相似对角化完成.

4 结果与讨论

由(20)式可知,A(1/2,1)的所有特征值都满足−1＜λk＜1,由于其特征值不为1,因此矩阵A(1/2,1)−E是可逆的.只要令Q=P,就可以利用(10)式给出容器底部压力分布fM与顶部压力分布f0的关系,即

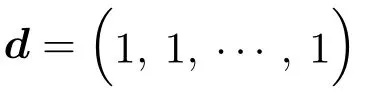
由于

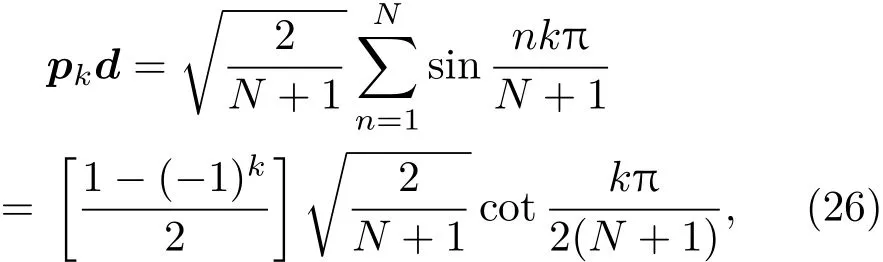
因此

显然(27)式中的求和部分只有当k取奇数时才有贡献.下面采用近似的方法讨论(27)式,一方面是因为不能严格地计算(27)式,另一方面是因为在实际问题中更关心M和N远大于1时Me随Mt变化的总趋势.记

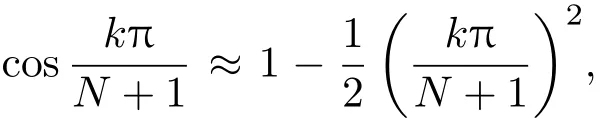
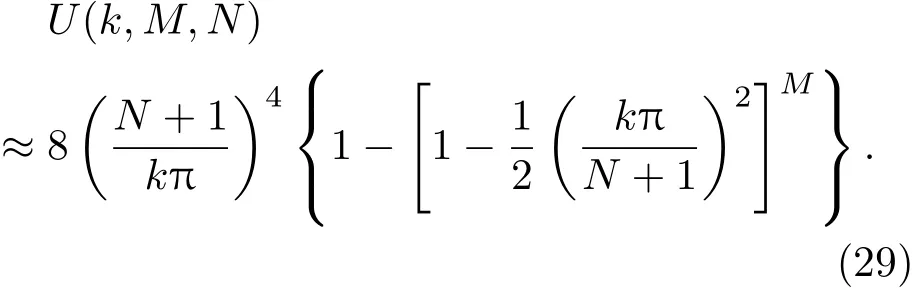
如果M的取值与N+1的平方有相同的量级,可设M=h(N+1)2,其中h可以反映竖直方向堆积的高度.则(29)式在N≫1时可简化为

将其代入(27)式,用求和部分的第1项代替整个求和部分,可以得到

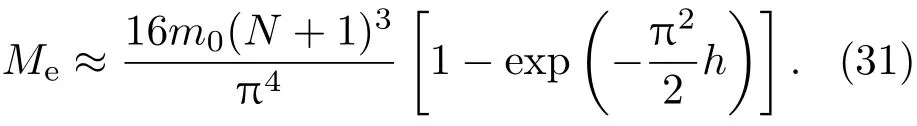
这与Janssen模型得到的(1)式类似,随着堆积高度的增加,有效质量逐渐增大,最后达到饱和.饱和质量满足Ms≈16m0N3/π4,总质量Mt≈m0hN3,(31)式可写为

这是格点系统模型在M和N远大于1并且取一级近似(即关于Me的求和式中只取k=1这一项)时得到的结果,与Janssen模型得到的(1)式在指数函数的系数部分有微小的差异,这说明pq模型中的力传递机理可以用于理解Janssen行为产生的原因.一方面,成拱效应使得颗粒能向其正下方的左右两侧传递力;另一方面,摩擦使得传递到边界的作用力可以被吸收.这两方面的因素相结合,产生了压力饱和.

传统的Janssen模型主要考虑容器底部总的压力[1,2].利用pq模型,可以从理论上考虑容器底部的压力分布问题.为简单起见,仍讨论顶部无负载的情形.由(24)式可得

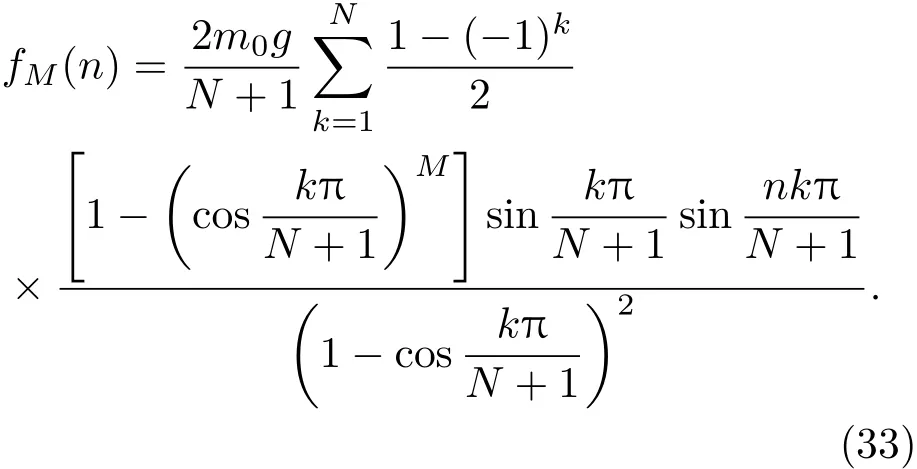
类似于有效质量的讨论,这里也采用近似的方法计算(33)式,在N远大于1且取一级近似的情况下,得到

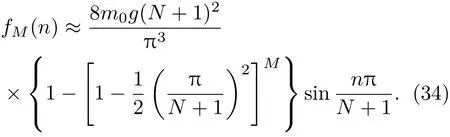
可以通过数值计算检验(34)式的近似程度,为此,设格点所受重力m0g为单位1,分别利用(33)式和(34)式计算压力分布fM(n)随M的变化.图3所示为精确解和近似解的数值计算结果,显然,只需取一级近似就能比较好地解决压力分布问题.从图3还可以看到,容器底部中央所受压力最大,从中央向两侧移动时压力逐渐减小.另外,在容器底部的某一固定位置处,随着堆积高度的增加,该位置处所受压力逐渐增大,最终会达到饱和.pq模型中力的传递类似于一维随机行走.在图2所示格点系统中,y轴相当于随机行走问题中的时间轴.随机行走问题在宏观上会导致扩散方程.实际上,将pq模型连续化后会得到带有吸收边界且含源的扩散方程.由于边界的吸收作用会随着堆积高度的增加逐渐由边界扩散到中央,因此产生了图3所示压力分布.如果将颗粒体系当作连续介质,应该采用应力分布函数σ(x,Ly)描述容器底部的压力分布情况.类似于有效质量的讨论,取M=h(N+1)2,利用(34)式、(2)式和(3)式,可以导出

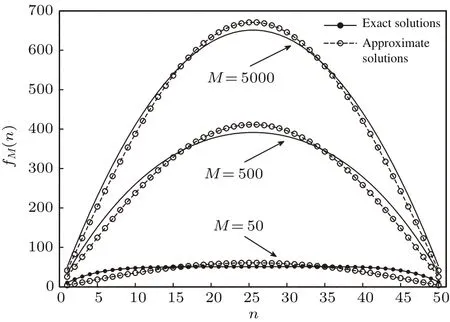
图3 压力分布随竖直方向层数M的变化Fig.3.Pressure distribution varies with the vertical layer number M.

式中β=Δy/Δx2是一个涉及格点系统模型微观特征的量,需要从微观上对颗粒堆积结构及相互作用进行分析才能确定.

由于一般情况下不能求出矩阵A(p,q)相似对角化后的解析结果,因此为了研究p和q对压力的影响,需要采用数值计算方法.由(4)式和(5)式可得

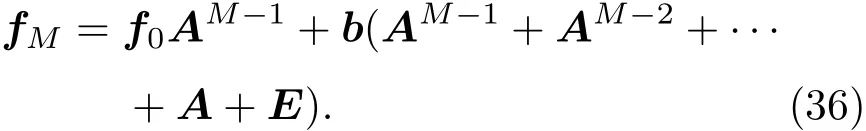
设m0g为单位1,在顶部无负载的情况下,利用(36)式可得底部总压力为

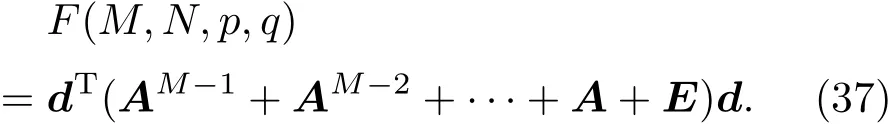
在Δx,Δy确定的情况下,可以用M和N分别代表颗粒堆积在竖直方向的高度和水平方向的长度.

下面用数值计算讨论p和q对压力-高度曲线F(M)的影响.如图4所示,当吸收系数或侧向传递系数为0时,压力只会随高度线性增加,不会出现压力饱和,这进一步说明了成拱效应与边界摩擦是产生压力饱和的主要原因.从图中还可以看到,随着吸收系数、侧向传递系数的增加,饱和压力的数值会减小.吸收系数越大代表边界因摩擦而产生的支撑作用越强,侧向传递系数越大代表内部颗粒的重力能更容易地传递到边界从而被支撑,因此产生了上述结果.

图4 (a)吸收系数p与(b)侧向传递系数q对底部总压力随堆积高度变化曲线的影响Fig.4.E ff ects of parameters(a)p and(b)q on bottom pressure variation with packing height.

5 结 论

研究筒仓中颗粒物质的微观力传递规则与宏观压力分布之间的关系,是深入了解颗粒介质力学性质的重要途径.传统的q模型可以比较好地解释随机堆积中力的概率分布、力的涨落等统计问题,这说明q模型至少在一定程度上正确反映了随机堆积中力传递的特征.为了研究筒仓中颗粒物质的压力、应力分布问题,本文针对二维随机堆积建立了一个类似于q模型的格点系统模型——pq模型.通过对p=1/2,q=1这一典型情况的解析计算结果可以看到:对于Me(Mt)关系,pq模型能给出与Janssen模型类似的结果;另外,pq模型还可用于讨论容器底部应力分布、点载荷下的响应等问题.不过应该注意到,尽管晶格堆积可以表现出与随机堆积不一样的力传递特征,但是晶格堆积模型也能导致与Janssen模型类似的Me(Mt)关系.如果统一采用格点模型理解问题,导致类似的结果来源于两种模型的共同性:格点能向其正下方左右两侧的格点传递力,边界处格点的总输入力会被吸收.可以看到,格点系统模型用于理解颗粒静力学问题时有其简单、方便之处,同时也可以拥有丰富的内容.本文讨论的pq模型只是格点系统模型中一种可能的力传递形式,对于不同的堆积结构和环境条件,可能具有不同的力传递规则,在数学上一般表现为不同的传递系数矩阵.这自然引入了一个值得深入研究的问题:力传递规则与堆积结构等因素之间有何种关系？另外,在p与q取一般数值的情况下,只要对A(p,q)进行适当的相似变换,就可将其转化为对称矩阵,并可利用文中提出的方法对其进行相似对角化,从理论上分析p,q等因素对有关压力问题的影响.但是这一过程的严格数学讨论十分繁琐,而且由于涉及非特殊性高次代数方程的求解,一般不能给出解析结果.如果将离散的格点系统模型连续化,利用其中的力传递规则给出应力函数σ(x,y)所服从的微分方程(相当于力传递方程连续化后的结果),pq模型会给出抛物线方程,利用偏微分方程理论可以比较容易地对问题进行求解.不过,离散的格点系统模型也有其优势,例如可以很方便地进行数值计算.

[1]Lu K Q,Liu J X 2004Physics33 629(in Chinese)[陆坤权,刘寄星2004物理33 629]

[2]de Gennes P G 1999Rev.Mod.Phys.71 374

[3]Vanel L,Claudin P,Bouchaud J P,Cates M E,Wittmer J P 2000Phys.Rev.Lett.84 1439

[4]Sun Q C,Hou M Y,Jin F 2011The Physics and Mechanics of Granular Matter(Beijing:Science Press)(in Chinese)[孙其诚,厚美瑛,金峰2011颗粒物质物理与力学(北京:科学出版社)]

[5]Bertho Y,Frédérique G D,Hulin J P 2003Phys.Rev.Lett.90 144301

[6]Peng Z,Li X Q,Jiang L,Fu L P,Jiang Y M 2009Acta Phys.Sin.58 2090(in Chinese)[彭政,李湘群,蒋礼,符力平,蒋亦民2009物理学报58 2090]

[7]Wambaugh J F,Hartley R R,Behringer R P 2010Eur.Phys.J.E32 135

[8]Li X Q,Jiang Y M,Peng Z 2010J.Shandong Univ.(Natural Science)45 101(in Chinese)[李湘群,蒋亦民,彭政2010山东大学学报45 101]

[9]Cambau T,Hure J,Marthelot J 2013Phys.Rev.E88 022204

[10]Li Z F,Peng Z,Jiang Y M 2014Acta Phys.Sin.63 104503(in Chinese)[李智峰,彭政,蒋亦民2014物理学报63 104503]

[11]Landry J W,Grest G S,Silbert L E,Plimpton S J 2003Phys.Rev.E67 274

[12]Marconi U M B,Petri A,Vulpiani A 2000Physica A280 279

[13]Zhang X G,Hu L,Long Z W 2006Chin.J.Comput.Phys.23 642(in Chinese)[张兴刚,胡林,隆正文 2006计算物理23 642]

[14]Jiang Y M,Zheng H P 2008Acta Phys.Sin.57 7360(in Chinese)[蒋亦民,郑鹤鹏 2008物理学报 57 7360]

[15]Gendelman O,Pollack Y G,Procaccia I 2016Phys.Rev.Lett.116 078001

[16]Liu C,Nagel S R,Schecter D A,Coppersmith S N,Majumdar S,Narayan O,Witten T A 1995Science269 513

[17]Coppersmith S N,Liu C,Majumdar S,Narayan O,Witten T 1996Phys.Rev.E53 4673

[18]Yang S L 2010Math in Practice and Theory40 155(in Chinese)[杨胜良2010数学的实践与认识40 155]

Lattice model for pressure problems in two-dimensional granular columns∗

Zhang Xing-Gang1)†Dai Dan2)

1)(College of Physics,Guizhou University,Guiyang 550025,China)
2)(College of Computer Science and Technology,Guizhou University,Guiyang 550025,China)

20 January 2017;revised manuscript

29 May 2017)

In order to make it easier to investigate some problems such as the mechanism of Janssen e ff ect and the stress distribution in granular medium,we simplify a granular column into a lattice system,in which a lattice point represents a small lump of granular medium and only neighbor interactions are considered.To study the disordered granular columns,a force propagation lattice model determined by the absorption coefficientpand the lateral transfer coefficientqis proposed,and this model is analyzed from the theoretical view.Firstly,the equation of force propagation in the matrix form is given,and this equation is determined by a tridiagonal matrixA(p,q)that is called transfer coefficient matrix.Based on the force transfer equation,the bottom force distribution varying with the top force distribution and the layer of lattice system is deduced,and its analytical solution refers to the similarity diagonalization of matrixA(p,q).Then,a method based on the second order di ff erence equations is proposed to obtain the eigenvalues and eigenvectors of the transfer coefficient matrix.The eigenvalues and eigenvectors ofA(p,q)can be rigorously deduced for a typical case,and with these results the pressure distribution relationship between the top and the bottom of the container is given.Based on these theoretical expressions,the relationship between the e ff ective mass and the total mass of granular medium is deduced,and it means that the force propagation model and the Janssen model can lead to similar results.Moreover,the bottom stress distribution is calculated without the top load.Calculations show that the stress distribution reaches a maximum at the center bottom and drops down to either side.Finally,numerical calculations are performed to investigate the e ff ects of parameterspandqon the relation between bottom pressure and packing height.Numerical results show that the saturated value of pressure decreases while parameterporqincreases.

Janssen e ff ect,stress distribution,lattice systems,tridiagonal matrix

(2017年1月20日收到;2017年5月29日收到修改稿)

10.7498/aps.66.204501

∗贵州省科技合作计划(批准号:20157641)、贵州大学引进人才科研基金(批准号:201334)和贵州大学教育教学改革研究项目(批准号:JGYB201517)资助的课题.

†通信作者.E-mail:xgzhang@gzu.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

PACS:45.70.–n,83.80.Fg,02.10.UdDOI:10.7498/aps.66.204501

*Project supported by the Science and Technology Cooperation Project of Guizhou Province,China(Grant No.20157641),the Scienti fi c Research Foundation for Talents of Guizhou University,China(Grant No.201334),and the Education and Teaching Reform Project of Guizhou University,China(Grant No.JGYB201517).

†Corresponding author.E-mail:xgzhang@gzu.edu.cn