陈志强王进良 李由

（北京航空航天大学数学与系统科学学院，北京 100191）

二维离散Duffing-Holmes系统的分支与混沌研究

陈志强†王进良 李由

（北京航空航天大学数学与系统科学学院，北京 100191）

通过欧拉方法可将Duffing-Holmes方程变换为离散非线性动力学系统，得到标准Holmes映射.研究该映射不动点的存在性与稳定性条件，并运用中心流形定理分析映射的Pitchfork分支，Flip分支和Hopf分支的存在性，具体给出了发生相应分支所满足的参数条件.此外，证明了映射存在Marotto意义下的混沌，最后用数值模拟验证了所得理论结果.

Duffing-Holmes系统， 不动点， 分支， Marotto混沌， 数值模拟

引言

G.Duffing在研究具有非线性恢复力项的受迫振动系统时，引入了具有立方恢复力项的非线性振子方程来描述力学问题中的加硬弹簧效应，它的标准化动力学方程就是著名的Duffing系统［1］.随着分支、混沌理论的不断进步与发展，以及计算机应用的深入，出现了许多试验模型来描述这个方程.其中，美国数学家P.Holmes提出了一种Holmes型Duffing 方程［2］，它的形式如下:

该连续系统的非线性动态，包括稳定性、分支及混沌等，已进行了广泛的研究［3-5］．然而在对Duffing方程进行MATLAB仿真时均采用了离散化的方法，鉴于目前对于离散的Holmes型Duffing方程的研究工作甚少，因此直接研究离散的Holmes型Duffing方程的动态行为具有很重要的意义．

本文选取 I（t）＝ 0，β＝1，利用欧拉方法可得:

令zn＝xn+Δtyn，并经过尺度变换上式可化为标准 Holmes 映射［6］，其具体形式为:

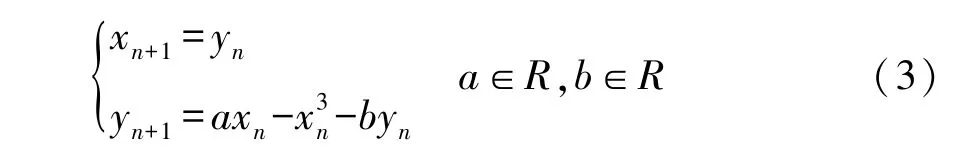
本文将针对该映射不动点的存在性、稳定性，局部分支，包括 Pitchfork、Flip、Hopf分支（或 Naimark-Sacker分支）等［7］，以及混沌存在性进行理论分析和数值模拟，得到了类似连续系统的复杂动态.所采用的方法与研究 Hénon 映射［8，9］类似，但 Hénon映射只有一个混沌吸引子，而Holmes映射由于具有立方项，会同时形成两个对称的混沌吸引子，因此，Holmes映射的动态将更为复杂．

1 系统不动点的存在性与稳定性

首先，映射（3）的不动点 z∗（x∗，y∗）满足如下方程:

解得 Z∗＝ （0，0）或（x±，y±），其中 x±＝ y±＝±a-b-1）．记 a0＝b+1，可得如下定理:

定理 1．1

（1）当 a＞a0时，映射（3）有三个不动点:

Z+（x+，y+）， Z-（x-，y-）和（0，0）；

（2）当 a＝a0时，映射（3）有三重不动点:

Z+＝Z-＝（0，0）；

（3）当 a＜a0时，映射有唯一不动点（0，0）．

下面讨论映射（3）的不动点Z∗的稳定性．映射（3）在Z∗点的Jacobian矩阵为:

其特征方程为:

通过对该条件的分析，可得如下定理:

定理 1．2

（1）映射（3）的不动点Z±稳定，当且仅当＜

2 系统分支的类型与稳定性

本节以a为分支参数，分别给出映射（3）在不动点Z∗处的Pitchfork分支，Flip分支和Hopf分支的充分条件．

2.1 Pitchfork分支

当a＝a0时，（0，0）处的 Jacobian矩阵的特征方程为:

其特征值为 λ1＝1，λ2＝-（b+1）．显然≠1当且仅当 b≠0，-2，并且当-2＜b＜0 时，＜1．

其中 g（u，μ，v）＝ μ（u+v）-（u+v）3．

设（u，μ，v）＝ （0，0，0）处的中心流形为:WC（0）＝｛（u，μ，v）｜v＝h（u，μ），h（0，0）＝ 0， Dh（0，0）＝ 0｝．

不妨设 h（u，μ）＝ αu2+βμu+γμ2+O（3），O（3）表示所有次数高于的余项和．由中心流形的不变性

知:

于是得到如下定理:

定理 1．3如果 b≠0，-2 且 a＝a0，则映射（3）在不动点（0，0）处经历 Pitchfork分支．当 a＞a0且-2＜b＜0时，映射（3）出现两个新的稳定不动点 Z+和Z-．

2.2 Flip分支

首先以Z+为例讨论Flip分支，类似可讨论Z-处与（0，0）处的 Flip 分支．

当 a＝1+2b≡a∗时，Z+处的 Jacobian 矩阵的特征方程为:

λ2+bλ+b-1＝0 （9）

其特征值为 λ1＝-1，λ2＝1-b．显然≠1当且仅当 b≠0，2，并且当 0＜b＜2 时，＜1．

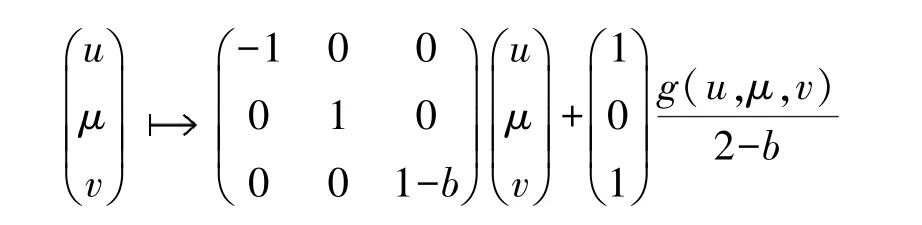
特别地，当 0＜b＜2 时，k1＞0，k2＜0．

综上，可以得到如下定理:

定理 1．4 如果 b≠0，2 且 a＝a∗，则映射（3）在不动点 Z+处经历 Flip分支．当 a＞a∗且 0＜b＜2时，从Z+处分支出不稳定的二周期轨．

2.3 Hopf分支

首先以Z+为例讨论Hopf分支（Naimark-Sacker分支），类似可讨论 Z-处与（0，0）处的 Hopf分支．

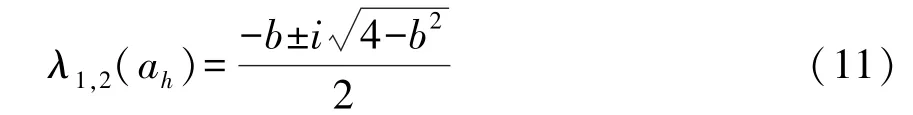
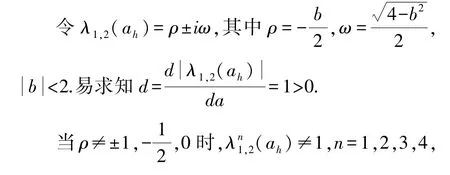
以上各导数均为在（0，0）处的取值．

综上，可以得到如下定理:

3 Marotto混沌的存在性

本节以Z+为例给出映射（3）存在 Marotto混沌［10］的条件，即给出 Z+为 snap-back-repeller的条件，类似可讨论Z-．

要求Z+为repeller，即 Z+处 Jacobian矩阵的特征值模大于1．对该条件分析整理可得如下引理:

引理1．1 若下列条件之一成立:

则 Z+为映射（3）的 repeller．

由迭代方程可得:

其中Z1（x1，y1）为（x0，y0）经过1次迭代得到的点．注意到 Z1≠Z+，整理可得:

4 数值模拟

4.1 对不动点的稳定性及其分支的数值模拟

本节给出一些数值模拟验证定理的结论．

（1） 令 b＝-0．5，a0＝ 0．5，ah＝ 1．25．由定理 1．2知，当 a∈（-1，0．5）时，不动点（0，0）是稳定的；当a∈（0．5，1．25）时，不动点 Z±是稳定的；由定理 1．3知，当a＝a0时，映射在不动点（0，0）处经历 Pitchfork分支．由定理1．5知，当a＝ah时，映射在不动点Z±处经历Hopf分支．如图1所示．

图1 b＝-0．5 分支图Fig.1 Bifurcation diagram when b＝ -0．5

（2） 令 b＝ 0．5，a0＝ 1．5，a∗＝ 2，ah＝ 2．75．由定理 1．2 知，当 a∈（-1，0．5）时，不动点（0，0）是稳定的；当 a∈（2，2．75）时，不动点 Z±是稳定的；由定理1.3知，当 a＝a0时，映射在不动点（0，0）处经历Pitchfork 分支．由定理1．4 知，当 a∈（2，2．75）时，映射在不动点Z±处经历不稳定的Flip分支．由定理1．5知，当a＝ah时，映射在不动点 Z±处经历 Hopf分支．如图2所示．

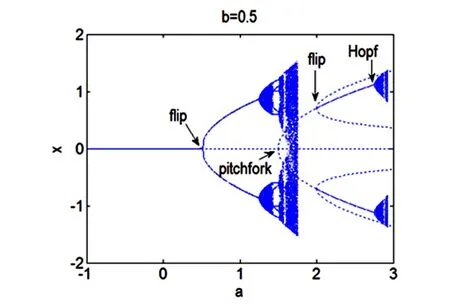
图2 b＝0．5 分支图Fig.2 Bifurcation diagram when b＝ 0．5

4.2 对混沌的数值模拟

本节利用分支图、最大Lyapunov指数图和相图来显示Marotto混沌的存在性，从而验证定理1．6的理论结果．

图3 b＝0．01 混沌分支图Fig.3 Bifurcation diagram of chaos when b＝ 0．01

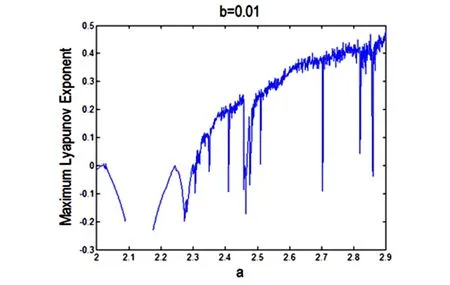
图4 b＝0．01最大 Lyapunov指数图Fig.4 Maximum Lyapunov exponent diagram when b＝ 0．01

图5 混沌相图Fig.5 Chaotic phase diagram

5 小结

本论文基于Duffing-Holmes方程的研究，首先将方程转换为二维离散非线性动力学系统，即标准Holmes映射，然后对该映射不动点的存在性进行分析，找出其稳定域.之后又详细分析了系统的Pitchfork、Flip、Hopf分支和 Marotto 混沌存在性，最后通过数值模拟验证了所得定理的结论.结果表明，Holmes映射最终会同时形成两个对称的混沌吸引子，其动态比Hénon映射更为复杂.

1 Cai M X，Yang J P， Deng J.Bifurcations and chaos in Duffng equation with damping and external excitations.Acta Mathematicae Applicatae Sinica， English Series， 2014，30（2）:483～504

2 王晓东.基于改进型Duffing振子的微弱信号检测研究.动力学与控制学报， 2016，14（3）:283～288 （Wang X D.Study of stochastic resonance based on Duffing oscillator.Journal of Dynamics and Control， 2016，14（3）:283～288（in Chinese））

3 Li Y，Yang B J，Lin H B，et al.Simulation and theoretical analysis on detection of the frequency of weak harmonic signals based on a special chaotic system.Acta Physica Sinica-Chinese Edition， 2005，54（5）:1994～1999

4 赵志宏，杨绍普，刘永强.基于Duffing振子的随机共振研究.动力学与控制学报，2014，12（2）:160～164 （Zhao Z H，Yang S P，Liu Y Q.Study of stochastic resonance based on Duffing oscillator.Journal of Dynamics and Control， 2014，12（2）:160～164 （in Chinese））

5 郭太银.随机激励下Holmes-Duffing系统的随机分形与分岔研究［硕士学位论文］.杭州:浙江大学航空航天学院，2007（Guo T Y.H Studies on the fractals and bifurcations of a Holmes-Duffing system under random excitations［Master Thesis］.Hangzhou:Zhejiang University of Aeronautics and Astronautics， 2007 （in Chinese））

6 王双连.动力系统中的混沌行为及其控制［博士学位论文］.杭州:浙江大学，2003（Wang S L.Chaotic motions and controlling chaos in dynamical systems［Ph.D Thesis］.Hangzhou:Zhejiang University， 2003 （in Chinese））

7 Wiggins.Introduction to applied nonlinear dynamical systems and chaos.New York:Springer-Verlag，1990

8 Hénon M.A two-dimensional mapping with a strange at-tractor.Communications in Mathematical Physics， 1976，50（1）:69～77

9 Jensen，Erik.A new construction of the unstable manifold for the measure-preserving Hénon map.Proceedings of the American Mathematical Society， 2008，136（1）:181～193

10 Marotto F R.Snap-back repellers imply chaos in Rn．Journal of Mathmatical Analysis＆ Applications， 1978，63（1）:199～223

ANALYSIS ON BIFURCATION AND CHAOS OF TWO-DIMENSIONAL DISCRETE DUFFING-HOLMES SYSTEM∗

Chen Zhiqiang†Wang Jinliang Li You
（School of Mathematics and Systems Science and LMIB， Beihang University， Beijing 100191， China）

Duffing-Holmes equation can be transformed into discrete nonlinear dynamical system by means of Euler′s method， and the standard Holmes map can be then obtained.The main purpose of this paper is to study the existence and stability of the fixed points of this Holmes map and to analyze the existence of Pitchfork bifurcation，Flip bifurcation and Hopf bifurcation of the map by using the center manifold theorem，and the conditions of the parameters corresponding to specific bifurcations are also given.In addition，it proves that the system is chaotic in the sense of Marotto.Finally，numerical simulations verify these theoretical results.

Duffing-Holmes system， fixed point， bifurcation， Marotto′s chaos， numerical simulation

29 November 2016，revised 13 December 2016.

10.6052／1672-6553-2017-011

2016-11-29收到第1稿，2016-12-13收到修改稿.

†通讯作者 E-mail:zhiqiangch＠buaa.edu.cn.

†Corresponding author E-mail:zhiqiangch＠buaa.edu.cn