胡亮 罗懋康

(四川大学数学学院,成都 610065)

柱面非线性麦克斯韦方程组的行波解

胡亮 罗懋康†

(四川大学数学学院,成都 610065)

(2017年2月3日收到;2017年4月16日收到修改稿)

柱面电磁波在各种非均匀非线性介质中的传播问题具有非常重要的研究价值.对描述该问题的柱面非线性麦克斯韦方程组进行精确求解,则是最近几年新兴的研究热点.但由于非线性偏微分方程组的极端复杂性,针对任意初边值条件的精确求解在客观上具有极高的难度,已有工作仅解决了柱面电磁波在指数非线性因子的非色散介质中的传播情况.因此,针对更为确定的物理场景,寻求能够精确描述其中更为广泛的物理性质的解,是一种更为有效的处理方法.本文讨论了具有任意非线性因子与幂律非均匀因子的非色散介质中柱面麦克斯韦方程组的行波精确解,理论分析表明这种情况下柱面电磁波的电场分量E已不存在通常形如E=g(r-kt)的平面行波解;继而通过适当的变量替换与求解相应的非线性常微分方程,给出电场分量E=g(ln r-kt)形式的广义行波解,并以例子展示所得到的解中蕴含的类似于自陡效应的物理现象.

柱面电磁波,非线性介质,行波解,自陡

1 引 言

电磁波按波面的形状一般有三种基本类型：平面波,柱面波和球面波.传统的非线性光学一般研究平面波与各种物质相互作用产生的非线性效应[1-3].柱面电磁波是几种基本的电磁波之一,它在各种非均匀非线性介质中的传播问题是一个重要又有趣的课题,可用于地球物理探测、微带天线技术[4,5]、铁电体分析[6]等领域.但由于柱面坐标系下的麦克斯韦方程组非常复杂,一直以来人们对柱面非线性光学的研究进展缓慢,寻找合适的数学和物理方法处理柱面电磁波在各种非均匀非线性介质中的传播问题也成为一个难题[7].

最近,Petrov和Kudrin[6,7]求出了柱面坐标系下具有指数非线性因子的非色散介质中麦克斯韦方程组的精确解,自此以后,柱面电磁波与相关的非线性光学现象获得了大量的关注与研究,各种研究成果也层出不穷.例如,Xiong等[8,9]将Petrov和Kud rin的结果进行了推广,指出他们的求解方法也适用于指数非线性因子与幂律非均匀因子相结合的介质;Xiong等[10-12]还讨论了柱面电磁波的二次谐波产生、和频与差频的产生等非线性光学现象;Chen等[13]研究了初值对柱面非线麦克斯韦方程组精确解的影响;Ranjbar和Bahari[14]则研究了柱面电磁波的四波混频效应.这些研究成果的基础都是Petrov和Kudrin所得到的精确解.实际上,精确解在解释与预言物理现象、开发新的近似计算方法等方面扮演着非常重要的角色[15-17].然而,目前人们还无法求出其他非线性介质中柱面电磁波的精确解.

柱面非线性麦克斯韦方程组没有一般的精确解求解方法[18,19],这时寻找满足某个特定条件的、有物理意义的解,是一种可行的途径.本文主要讨论电磁波理论特别是孤立波理论中极为重要的一类解--行波解[20-25].从已有的资料看来,目前对柱面非线性麦克斯韦方程组行波解的研究尚未展开.在Petrov和Kudrin工作的基础上,我们提出一种方法来求得在具有任意非线性因子与幂律非均匀因子的非色散介质中传播的柱面电磁波的行波精确解,并研究其物理性质和意义.本文的组织结构如下：第二部分介绍所使用的物理模型;第三部分先指出所讨论模型的电场分量已不存在通常形如E=g(r-kt)的平面行波解,然后给出E=g(ln r-kt)形式的广义行波精确解[26];第四部分讨论所得的广义行波解与平面行波解的异同;第五部分进行总结.

2 柱面电磁波模型

本文使用文献[6-14,18,19,27]工作中相同的物理模型.考虑一个无损耗、非磁性介质中的电磁场,并假设介质拥有一个对称轴,将对称轴设为

z轴,建立柱面坐标系(r,φ,z).我们进一步假设电磁场与φ和z无关,且电场部分平行于对称轴z,同时忽略色散效应,那么我们可以得到如下的柱面麦克斯韦方程组：

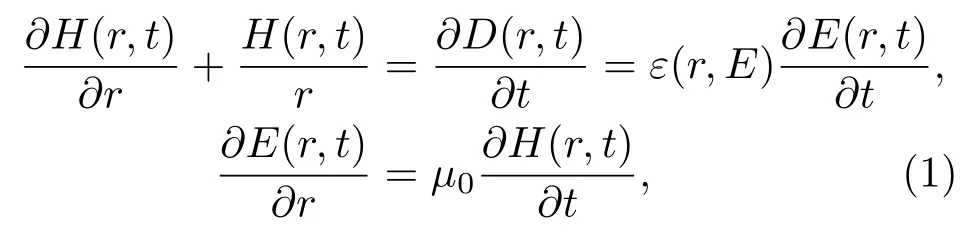
这里µ0是真空磁导率;r,t分别表示半径和时间;E,H,D分别表示电场、磁场和电位移; ε(r,E)=d D/d E是介质的介电函数,不同的ε(r,E)所描述的介质性质也有所不同.在本文中,我们研究非均匀非线性介质

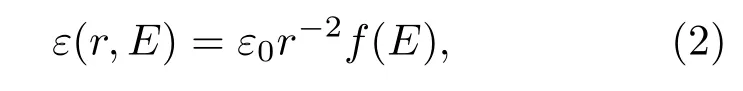
其中ε0是真空电容率,f是任意可导函数.这个介电函数表明我们要研究的介质具有幂律非均匀因子r-2,而非线性因子可以是任意的.实际上,随着材料科学的发展,现在通过超材料几乎可以构造出具有任何性质的介质[28-31].当非线性因子f(E)取成指数函数的形式：f(E)=exp(αE),其中α是描述介质特性的常数,方程组(1)就变成Petrov和Xiong等所讨论的情况[6-14,18,19,27].

3 行波解

本文只考虑电场分量E(r,t)的行波精确解,这时磁场分量H(r,t)的解可通过对方程组(1)积分得到.我们指出方程组 (1)与 (2)不存在形如E(r,t)=g(r-kt)的非平凡平面行波解,其中g为任意可导函数,k为表示波速的任意常数.这里非平凡意味着E不恒为常数,以及k/=0.

实际上,消去麦克斯韦方程组(1)与磁场H有关的项后,我们得到如下二阶非线性偏微分方程：

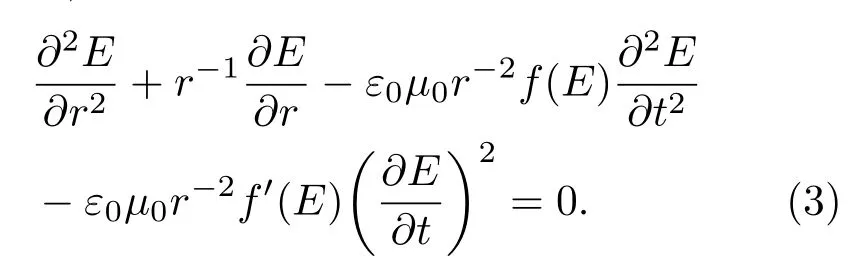
若是电场E具有形式E=g(r-kt),令w=r-kt,将E=g(w)代入偏微分方程(3),经过一些计算后可得：

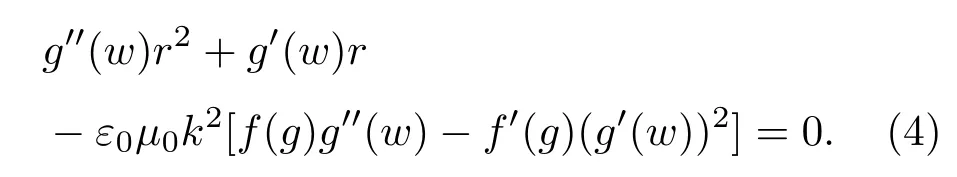
方程 (4)可以看成关于变量r的代数方程,解出r得到：

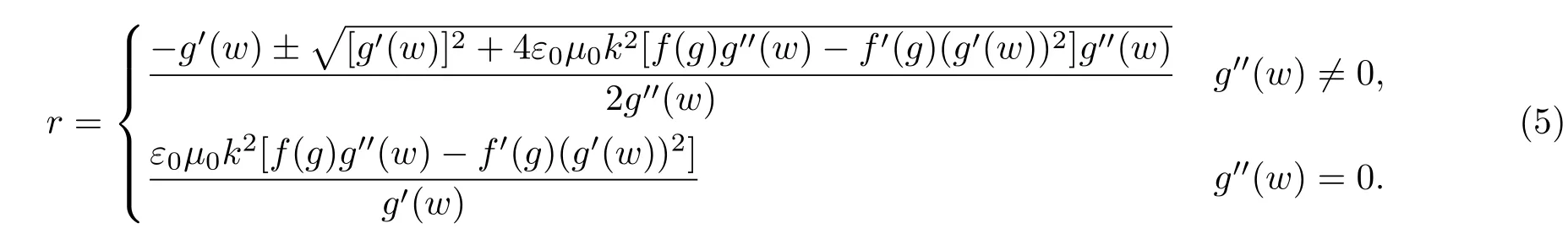
这个等式与此前w=r-kt的定义相矛盾,从而表明E=g(w)=g(r-kt)的假设不能成立.

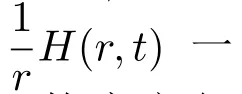
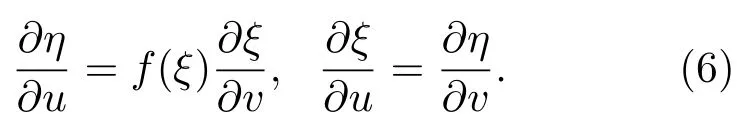
对方程组(6)消去η变量,可得：

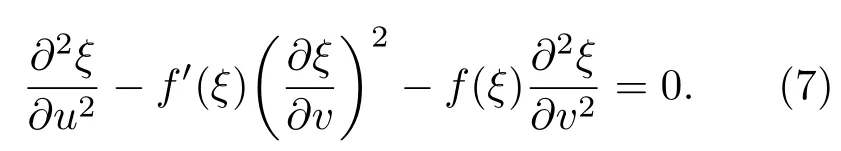
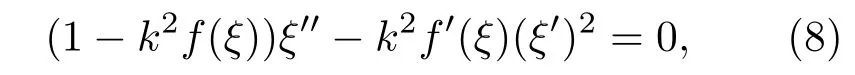
化简非线性常微分方程(8),可得

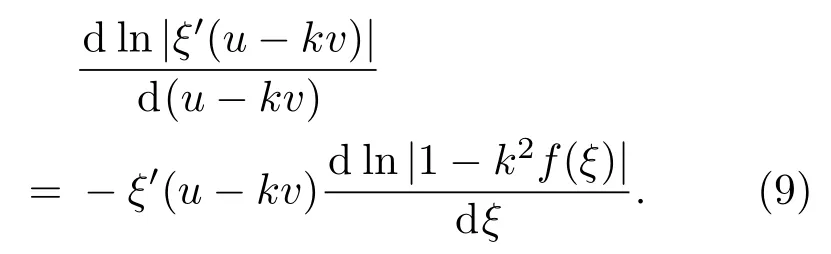
微分方程(9)的解可由隐函数表示：

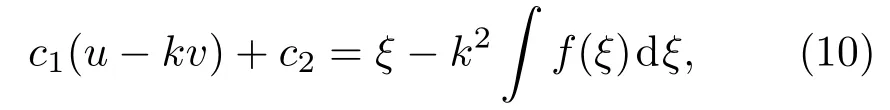
其中c1,c2是任意常数.(10)式给出了方程组 (6)中ξ函数的平面行波解.我们将(10)式中u,v分别由原来的变量r,t替换,便可得到柱面非线性麦克斯韦方程组(1)与(2)的广义行波解：

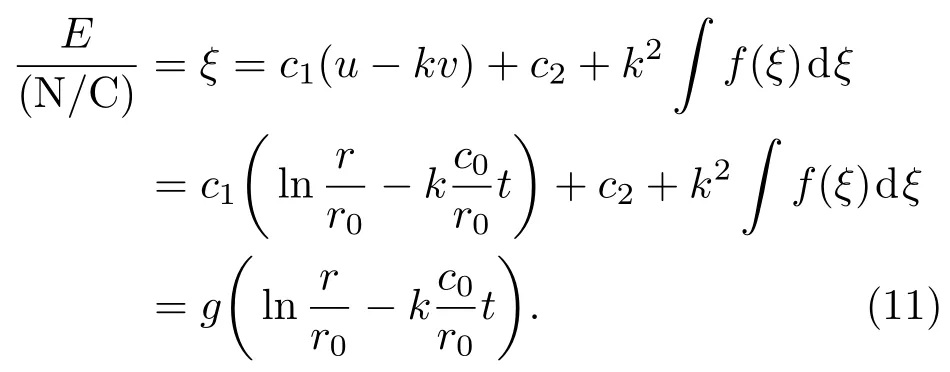
这里c0=(ε0µ0)-1/2表示真空光速,函数g是由非线性因子f(ξ)决定的函数;其他符号如前所述, (N/C)表示电场E在国际单位制下的单位,c1及c2表示任意常数,r0表示一个具有长度量纲的常数, k则是表示波速的无量纲常数.注意若k取负值,那么随着时间的增加柱面波会向半径减小的方向传播;反之,则向半径增大的方向传播.在忽略反射的情况下,如果激发柱面行波 (11)的激励源在柱心处,则行波会向外(半径增大的方向)传播,此时k＞0;如果激励源在r=R处,为便于讨论,我们将介质(2)的边界取为R,则对于R之内的区域而言,行波是向内(半径减少的方向)传播的,此时k＜0.向外传播的柱面行波(11)相当于向内传播情况的时间反演,即对于柱心处的激励源,我们可以找到一个边界r=R处的镜像源,该镜像源在R之内激发的行波按时间t负方向的演化等价于柱心源激发的行波按时间t的演化,因此接下来我们只讨论源在边界处的情况.此时由源激发的柱面行波(11)的初始加速度必定要满足

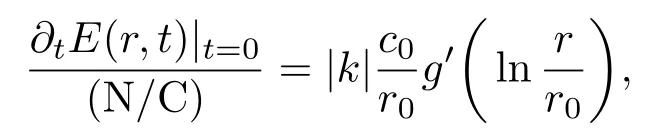
而边界值要满足

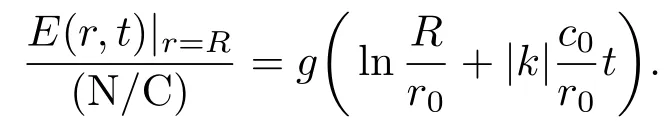
4 解的物理意义

我们在这一部分讨论所获得的行波解 (11)的物理意义. 考虑一个半径为R的圆柱形腔体,其中填满非均匀非线性非色散介质ε(r,E)=,这种介质的典型代表是铁电体[32,33].取r0=1(m),,c1=1, c2=0,其中(m),(m/s)分别为国际单位制下长度和速度的单位.则由(11)式可得柱面电磁波(1)式电场分量的行波解为

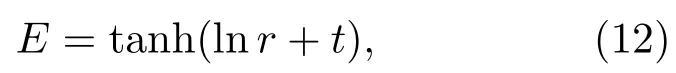
由此解可以很容易构造出所需的初边值条件：

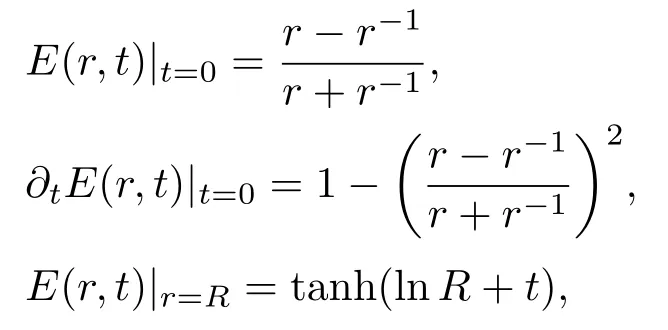
其中各物理量的单位已被消除,E,r与t分别表示无量纲的电场、半径与时间.

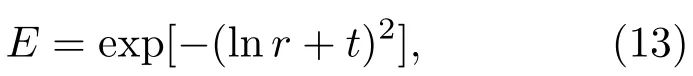
初边值条件为

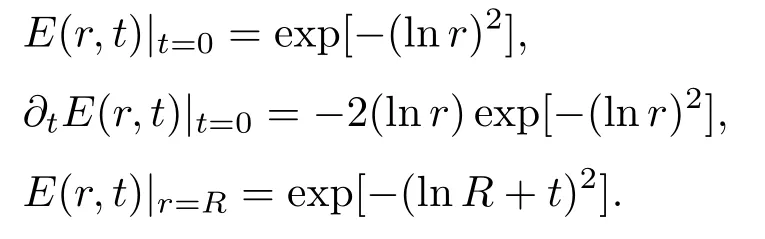
同样,E,r与t分别表示无量纲的电场、半径与时间.

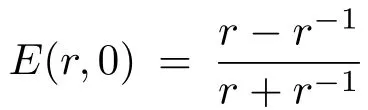
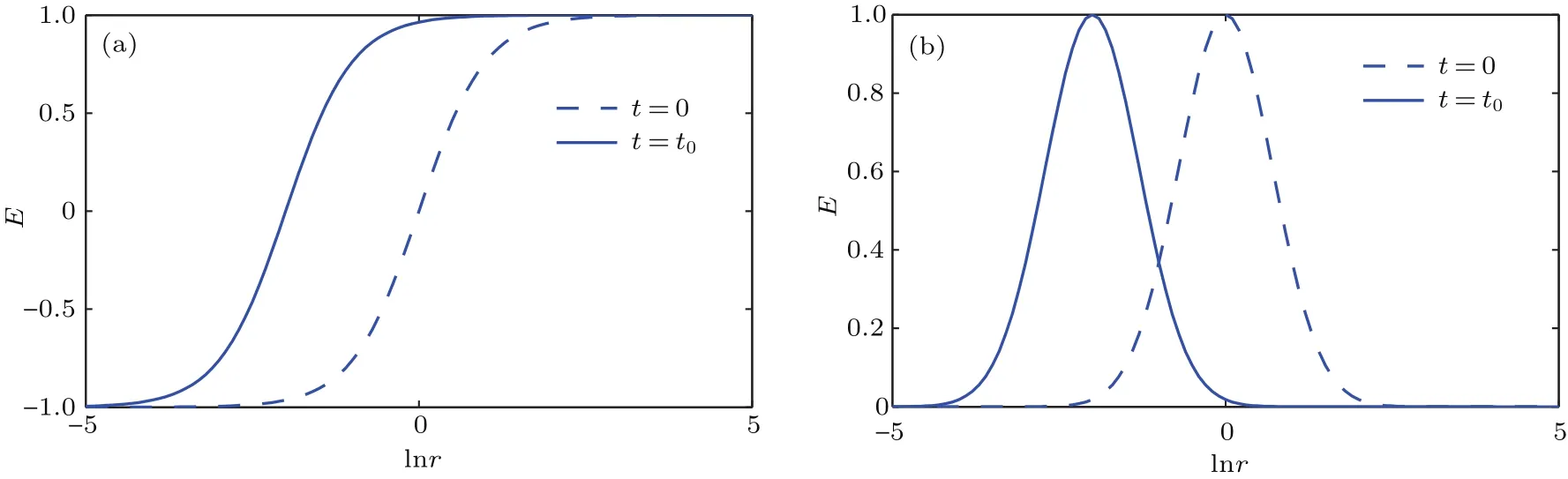
图1 (a)行波解(12)的电场与ln r在不同时刻的关系;(b)行波解(13)的电场与ln r在不同时刻的关系Fig.1.(a)The electric field of traveling wave solu tion(12)as function of ln r at various times;(b)the electric field of traveling wave solution(13)as function of ln r at various times.

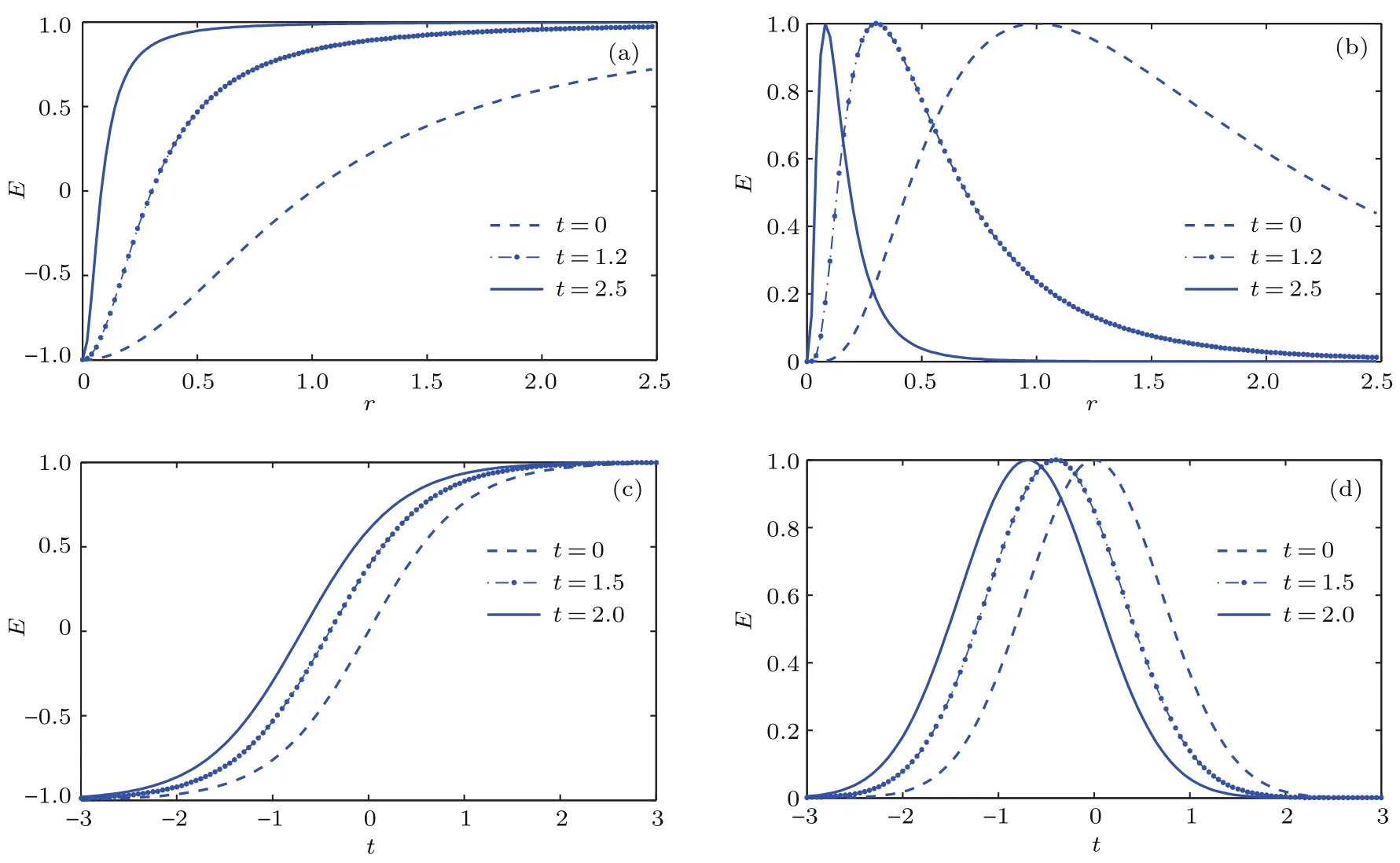
图2 (a)行波解(12)的电场与r在不同时刻的关系;(b)行波解(13)的电场与r在不同时刻的关系;(c)行波解(12)的电场与t在不同位置处的关系;(d)行波解(13)的电场与t在不同位置处的关系Fig.2.(a)The electric field of traveling wave solu tions(12)as function of r at various times;(b)the electric field of traveling wave solutions(13)as function of r at various times;(c)the electric field of traveling wave solutions (12)as function of t at different locations;(d)the electric field of traveling wave solutions(13)as function of t at d iff erent locations.

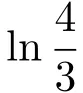
显然,不论(11)式中的函数g取何种形式,只要波速参数k＜0,电场的波形在半径越小的地方就会推进得越慢,而在半径越大的地方推进得越快,从而波形会变得越来越陡;理论上当时间t=+∞时,在r=0处会形成冲击波.

5 结 论

柱面非线性麦克斯韦方程组的求解是目前的研究热点与前沿之一,但由于它在数学上的极端复杂性,在任意初边值条件下,目前人们只对一类非线性形式给出了精确解,进一步的研究遇到了很大的困难.在本文中,我们在某些特定的初边值条件下,针对更为广泛的非线性情形,讨论柱面非线性麦克斯韦方程组的行波精确解.通过研究发现所讨论的柱面电磁模型没有普通的平面行波解,而是存在一种广义的行波解.这个广义的行波解有着独特的性质：随着位置的不同,电场波形的传播速度也不同,从而会形成某种类似于自陡的现象.通过设计特殊的结构与合适的激励源,我们的工作在实际中对铁电体分析、新型材料的电磁性质研究等有一定意义,在理论上则为柱面非线性麦克斯韦方程组的研究提供了新的思路与结论.

感谢陈凯杰博士和张霄博士的讨论和帮助.

[1]Ye P X 2007 Non linear Optical Physics(Vol.1)(Beijing: Peking University Press)pp17-18(in Chinese)[叶佩弦2007非线性光学物理(北京:北京大学出版社)第17—18页]

[2]Yao B,Zheng Q H,Peng J H,Zhong R N,X iang T,Xu W S 2011 Chin.Phys.Lett.28 118401

[3]Zhang M,Li L S,Zheng N,Shi Q F 2013 Chin.Phys. Lett.30 077802

[4]Chew W C 1990 W aves and Fields in Inhom ogeneous M edia(New York:Van Nostrand Reinhold)p161

[5]Ertürk V B,Ro jas R G 2003 IEEE Trans.An tenn. Propag.51 739

[6]Petrov E Y,K ud rin A V 2010 Phys.Rev.Lett.104 190404

[7]K ud rin A V,Petrov E Y 2010 JETP 110 537

[8]X iong H,Si L G,Huang P,Yang X 2010 Phys.Rev.E 82 057602

[9]X iong H,Si L G,D ing C,LüX Y,Yang X,W u Y 2012 Phys.Rev.E 85 016602

[10]X iong H,Si L G,D ing C,Yang X,W u Y 2011 Phys. Rev.A 84 043841

[11]X iong H,Si L G,Guo J F,LüX Y,Yang X 2011 Phys. Rev.A 83 063845

[12]X iong H,Si L G,D ing C,Yang X,W u Y 2012 Phys. Rev.E 85 016606

[13]Chen S Y,Li T,X ie J B,X ie H,Zhou P,Tian Y F, X iong H,Si L G 2013 Phys.Rev.E 88 035202

[14]Ran jbar M,Bahari A 2016 Opt.Comm un.375 19

[15]Zhang S Y,M a X R,Zhang S G,Chen L,W ang X Y, M u K L,Wang S 2014 Chin.Phys.B 23 060304

[16]Zhang C Q,Ruan C J,Zhao D,W ang S Z,Yang X D 2014 Chin.Phys.B 23 088401

[17]Liu L X,Shao C G 2012 Chin.Phys.Lett.29 111401

[18]Es’kin V A,Kud rin A V,Petrov E Y 2011 Phys.Rev. E 83 067602

[19]X iong H,Si L G,Yang X X,W u Y 2015 Sci.Reports 5 11071

[20]G ren fell B T,B jornstad O N,Kappey J 2001 Nature 414 716

[21]Shi L F,Zhu M,Zhou X C,Wang W G,M o J Q 2014 Acta Phys.Sin.63 130201(in Chinese)[石兰芳,朱敏,周先春,汪维刚,莫嘉琪2014物理学报 63 130201]

[22]Xu Y H,Han X L,Shi L F,M o J Q 2014 Acta Phys. Sin.63 090204(in Chinese)[许永红,韩祥临,石兰芳,莫嘉琪2014物理学报63 090204]

[23]Harko T,M ak M K 2015 J.M ath.Phys.56 111501

[24]Sardar A,Husnine SM,Rizvi S T R,Younis M,Ali K 2015 Non linear Dynam.82 1317

[25]W ang M L,Li X Z,Zhang J L 2008 Phys.Lett.A 372 417

[26]Shu Y Q 2011 Ph.D.Dissertation(Lanzhou:Lanzhou University)(in Chinese)[舒雅琴2011博士学位论文(兰州:兰州大学)]

[27]Petrov E Y,Kud rin A V 2012 Phys.Rev.E 85 055202

[28]Silva A,M onticone F,Castald i G,Gald i V,AlùA,Engheta N 2014 Science 343 160

[29]Eid ini M,Pau lino G H 2015 Sci.Adv.1

[30]M a G,Sheng P 2016 Sci.Adv.2

[31]Fan W,Yan B,W ang Z B,W u L M 2016 Sci.Adv.2

[32]Chen H W,Yang C R,Fu C L,Zhao L,Gao Z Q 2006 Appl.Surf.Sci.252 4171

[33]Fong D D,Stephenson G B,Streiff er S K,Eastm an J A, Auciello O,Fuoss P H,Thom pson C 2004 Science 304 1650

[34]Han SH,Park Q H 2011 Phys.Rev.E 83 066601

[35]Shafeeque Ali A K,Porsezian K,U thayakum ar T 2014 Phys.Rev.E 90 042910

[36]Reed E J,SoljačićM,Gee R,Joannopou los J D 2007 Phys.Rev.B 75 174302

[37]G rischkow sky D,Du ling III IN,Chen JC,ChiC C 1987 Phys.Rev.Lett.59 1663

(Received 3 February 2017;revised manuscript received 16 April 2017)

Traveling wave solutions of the cylindrical nonlinear Maxwell’s equations

Hu Liang Luo Mao-Kang†

(Departm ent ofM athem atics,Sichuan University,Chengdu 610065,China)

Study on p ropagation of cy lind rical electrom agnetic waves in various inhom ogeneous and nonlinear m edia is of fundamental importance,which can be described by the cylindricalnonlinear Maxwell’sequations.In recent years,finding exact solutions for these equations has em erged as a popular research topic.The exact solutions play an irrep laceable role in understanding and predicting physical phenomena,and developing numerical calculation methods,and so on. However,due to the extrem e com plexity of nonlinear partial differential equations,exact solutions of the cylindrical M axwell’s equationswere only ab le to be obtained in a nonlinear and nondispersivem edium whose dielectric function is an exponential function in previous researches.Actually,there is no generalmethod at present which can exactly solve arbitrary cy lind rical nonlinear M axwell’s equations.Therefore,finding physically adm issib le solutionsm eeting certain particu lar condition for the cylindrical nonlinear M axwell’s equationsmight be feasible.

In this paper,we discuss the traveling wave solutionswhich are very im portant in electromagnetic theory,especially in solitary wave theory.To our know ledge,research on obtaining traveling wave solutions of the cylindrical nonlinear M axwell’s equations is still lacking.Them ain conclusions in this paper are listed as follow s.

Firstly,we introduce the cy lind rical nonlinear Maxwell’s equationsmentioned in some previous publications,which can describe cylindricalelectrom agnetic waves propagation in inhom ogeneous nonlinear and nondispersivem edia.In this paper,we focus on the nondispersivem edia with arbitrary nonlinearity and power-law inhom ogeneity.

Second ly,we point out that the electric field com ponent E of the model has no p lane traveling wave solutions E=g(r-kt),after theoretical analysis and study.Then generalized traveling wave solutions in form of E=g(ln r-kt) for the electric field com ponent are obtained by finding correct variable substitution and solving second-order nonlinear ordinary differential equation.

Finally,we p rovide two exam p les to show the physicalm eanings of our generalized traveling wave solutions.We find that the transm itting speeds of vibrations vary with different points of the electric field.Actually,the transm itting speed of the vibration of a certain point closer to the cylinder center is lower.As a resu lt,we observed a physical phenom enon sim ilar to that of“self-steepening”.

Our work can be used to analyze the electromagnetic properties of ferroelectric materials and new materials. Theoretically,it can also provide an approach to studying the cylindrical nonlinear M axwell’s equations.

cylindrical electromagnetic waves,nonlinearmedia,traveling wave solutions,self-steepeningPACS:03.50.De,02.30.Jr DO I:10.7498/aps.66.130302

PACS:03.50.De,02.30.Jr DO I:10.7498/aps.66.130302

†通信作者.E-m ail:m akaluo@scu.edu.cn

†Corresponding author.E-m ail:m akaluo@scu.edu.cn