刘景良，郑文婷，黄文金，黄志伟

(1.福建农林大学 交通与土木工程学院，福州 350002；2.福建工程学院 土木工程学院，福州 350118）

一种识别Duffing非线性系统刚度的新方法

刘景良1，郑文婷2，黄文金1，黄志伟1

(1.福建农林大学 交通与土木工程学院，福州 350002；2.福建工程学院 土木工程学院，福州 350118）

振动响应的频率变化与位移、速度、振幅息息相关，基于非线性振动系统的这一主要特征提出一种新的识别Duffing非线性系统刚度的方法。该方法首先通过Lindestedt-Poincaré法建立Duffing非线性系统瞬时幅值与瞬时频率的关系式，然后分别采用Hilbert变换和最大坡度法提取非线性系统响应的瞬时幅值和瞬时频率。在此基础上，应用最小二乘优化算法识别非线性系统的线性和立方体刚度。通过一个Duffing非线性系统数值算例对所提出的新方法进行验证，结果表明：即使在信号被噪声干扰的情况下，该方法仍然能够有效识别Duffing非线性系统的刚度。

振动与波；Duffing非线性系统；最大坡度法；最小二乘法；瞬时频率；瞬时幅值

非线性问题普遍存在于土木工程结构中，如循环荷载下钢结构连接螺栓的松紧，风与车辆荷载引起的斜拉桥的拉索索力的变化等，此外，结构的损伤也会引发非线性行为。适用于线性系统的叠加原理往往无法解释非线性问题所表现出来的复杂力学行为，因此建立描述非线性系统特性的模型并准确识别非线性结构的特征参数成为当前非线性系统研究的热点问题。总的来说，非线性振动系统的识别方法分为基于信号处理技术的方法[1–4]、增量谐波法[5]、时间序列分析类方法[6–7]、子空间类方法[8]、高阶谱[9]等方法。由于非线性系统最显著的一个特征就是系统振动响应的频率变化与振幅、位移、速度息息相关，其响应信号呈现非平稳性，而传统的时域和频域分析方法难以全面反映非平稳响应信号的时频特性，因此以小波变换(Wavelet transform,WT)[10–11]为代表的时频分析方法近年来广泛应用于非线性结构系统的参数识别。如Shi等结合经验模态分解和Hilbert变换方法识别了多自由度时变系统的刚度和阻尼[12]。Tjahjowidodo等分别采用Hilbert变换和连续小波变换的方法识别出非线性结构的瞬时特性，并将提出的方法用于非线性结构系统的识别[13]。Yan等在采用Hilbert变换提取结构系统瞬时特征参数的基础上，利用瞬时特征参数与结构系统物理参数之间的时变特性建立回归模型，然后通过最小二乘法成功识别了结构的物理参数[14]。但是，Hilbert变换这一类方法对噪声较为敏感，只在结构系统为弱阻尼和噪声水平较小时识别结果才比较精确。通常情况下，基于小波变换的非线性系统参数识别结果优于基于Hilbert变换的参数识别结果。而基于小波变换识别非线性系统参数的关键问题是如何得到清晰的时频曲线。邓杨等利用多项式调频小波对非线性系统的瞬时特性进行了提取，并结合FREEVIB和FORCEVIB方法中瞬时模态参数的算法，得到了能直观反映结构系统非线性的骨架曲线和阻尼系数曲线，但是该方法在提取瞬时频率特性时利用了频率迹线具有连续性、平滑性的先验信息[15]。任宜春等基于复Morlet小波系数模局部极大值识别了Duffing非线性系统的瞬时频率和瞬时振幅，然后通过曲线拟合得到系统的阻尼系数和非线性系数[16]。代煜等利用脊线上连续小波变换系数的幅度和相位信息，从结构系统的自由衰减响应中辨识了弱非线性阻尼和刚度[17]。然而，无论是基于小波系数模值还是基于小波系数相位信息的小波脊线提取方法，都面临着一个同样的问题，即提取的小波脊线存在许多毛刺，识别的瞬时频率精度不高，从而影响了系统物理参数的识别。Wang等提出的基于动态规划的时变结构瞬时频率提取方法在一定程度上消除了端点效应，但其算法较为复杂[18]。同步挤压小波变换(Synchrosqueezing wavelet transform，ST)通过重组小波变换后的时频图获得了较高频率精度的时频曲线[19–20]，但是该方法只能处理信号在频率不变时尺度方向的扩散，对于时间维度上的扩散却无能为力。

基于此，本文首先采用Lindestedt-Poincaré法建立Duffing非线性系统瞬时幅值与瞬时频率的关系式，然后通过Hilbert变换求解瞬时幅值并提出最大坡度法(Maximum gradient,MG)识别Duffing非线性结构系统响应的瞬时频率，该方法避免了基于小波系数模局部极大值的脊线提取方法中出现的毛刺现象和同步挤压小波变换仅提高时频曲线频率精度的问题。在有效提取瞬时特征参数的基础上，运用最小二乘拟合方法识别了Duffing非线性结构系统的刚度，该方法具有一定的抗噪性。

1 非线性系统特征描述

通常情况下，能够得到精确解析解的非线性结构系统极少，因此摄动法等近似解法成为求解非线性系统的可行方法。Lindestedt-Poincaré法[21]为摄动法的一种，又称为PLK法，其基本原理为：在将非线性结构系统方程的基本解展开成ε的幂级数的同时，将频率ω用ε的幂级数表示，而幂级数的待定系数则根据周期运动的要求依次求解。通过PLK法构建瞬时频率与瞬时幅值的关系式，从而为骨架曲线和物理参数的识别提供了一条可行的途径。

对于含小参数的Duffing非线性系统方程，可以表示为

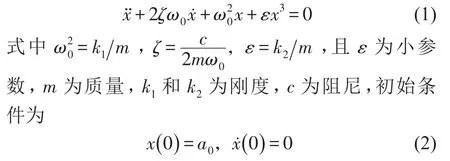
首先引入新变量τ=ωt，则式(1)转化为

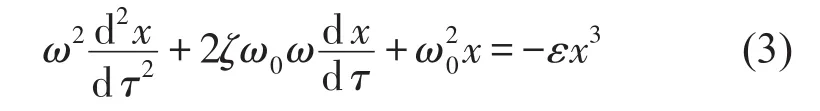
然后将x和ω分别展开成ε的幂级数

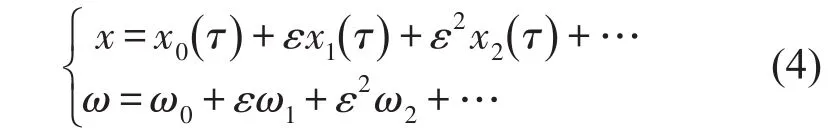
将式(4)代入方程(3)可得

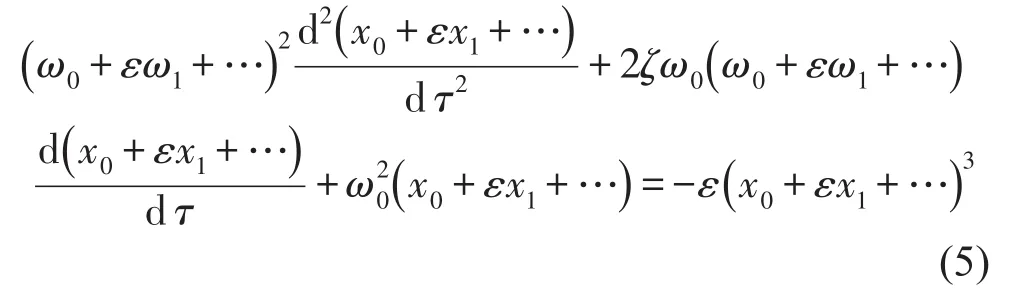
令式(5)中ε的同次幂的每一项系数为零，可求得其零级近似和一级近似分别为

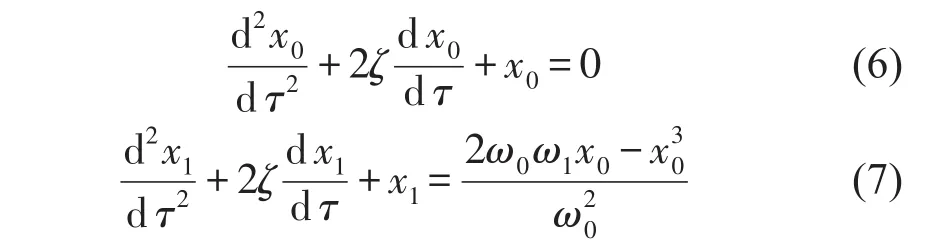
显然，零级近似方程式(6)的通解为

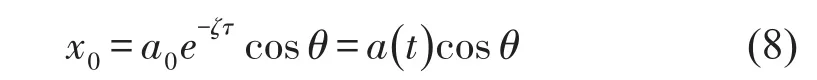
式中a(t)为瞬时幅值而a0和θ0为预先任意给定的初始幅值和初始相位。将式(8)代入式(7)，得

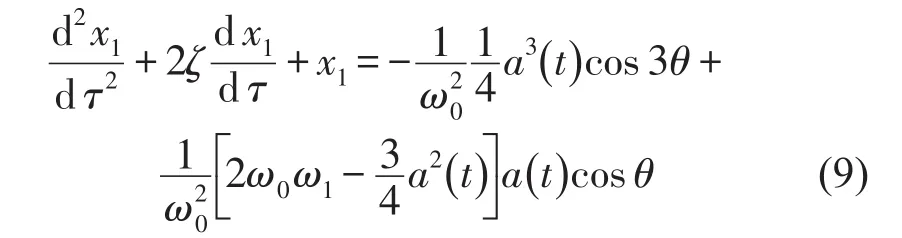
为避免式(9)的解中出现久期项，以保证x1的周期性，须令方程的右边a(t) cosθ项的系数为零，即

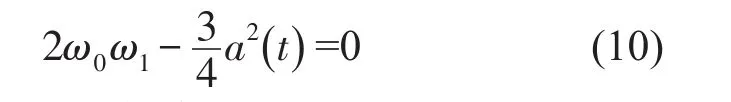
因此，ω的一级近似为

将式(11)代入式(4)，可得

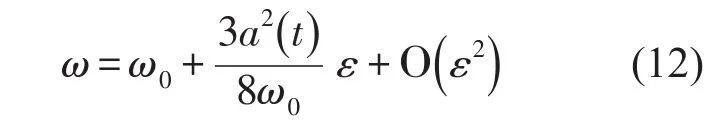
式(12)只是根据Duffing非线性方程的一级近似得到的瞬时频率与瞬时幅值的关系式。二级近似乃至更高级的近似可以得到更为精确的结果，但是对于土木工程实际结构，一级近似的结果通常已经足够。

2 非线性系统瞬时特征提取

由上述非线性特征描述过程可知，响应信号瞬时特征参数的成功提取是整个非线性系统识别过程中的关键。其中瞬时幅值的提取可通过Hilbert变换实现。定义为响应信号的解析信号，则位移瞬时幅值A()t可通过求解解析信号X(t)的模值获得，即

瞬时频率的估计也可通过Hilbert变换来实现。但是相关研究表明：Hilbert变换在识别瞬时频率时对噪声较为敏感[15]。而小波变换由于其具有良好的时频局部化特性，可更为客观地反映结构系统瞬时特征参数的变化，因而十分适合时变和非线性结构系统的参数识别。小波脊线的提取是采用小波变换方法识别信号瞬时频率的关键问题之一。目前提取小波脊线的方法主要有两种[18]：一种是基于小波系数的相位信息，一种是基于小波系数的模信息。然而，这两种方法都面临着一个同样的问题，即提取的小波脊线中存在许多毛刺，影响了时频曲线的光滑性，从而大大降低了信号瞬时频率的识别精度。为此，本文提出了一种基于最大坡度的小波脊线提取方法，其基本理论如下：任意实信号x(t)经过连续小波变换后，其时间b(t)、尺度a或频率f，小波系数的绝对值组成一个三维空间坐标系(x，y，z)，形似一座山峰，其中b和a(f)构成了二维的时间-尺度(频率)平面，即山峰的长度和宽度方向，而的值的大小代表了z方向的距离，即山峰的高度。从山脚预先设定的起始点出发，在一定范围内搜索前进，由于山脊的走向最为陡峭，即坡度最大，因此将该方向上的各点连接成线即为待提取的小波脊线。

(a)设定连续小波变换共有m个尺度，从小到大分别记为而时间点则记为实信号x(t)经连续小波变换后，其小波系数Wx为m×n矩阵，绘出的小波量图如图1所示。

则Si与Si-1两点在时间-尺度平面的距离为

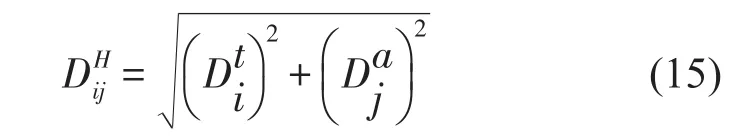
而Si与Si-1两点在z方向的距离为

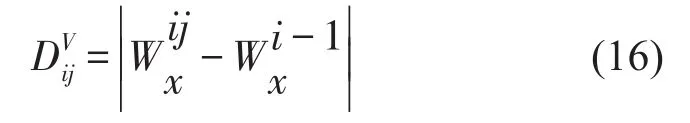
根据式(15)和式(16)，Si与Si-1两点之间的坡度为

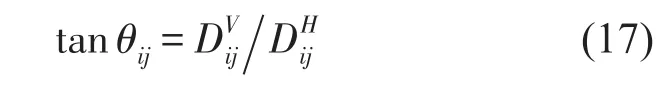
(d)寻找出tanθ最大值，即为最大坡度

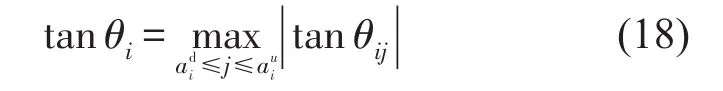
(e)根据最大坡度tanθi，求出对应的尺度值ai，并根据ai和ti在小波系数矩阵中寻找出相应的小波系数值的三维坐标此时均为已知。而该点的频率值可以通过尺度与频率的对应关系求解。

(f)重复(c)－(e)步骤并进行下一步的搜索，直至原始信号末端结束。最后将各点频率值连接成线，得到所求的小波脊线和时频曲线。

3 最小二乘法识别刚度

从响应信号中提取出瞬时频率和瞬时幅值之后，可将式(12)视为Duffing非线性系统刚度参数识别的回归模型，则回归模型中所有的未知系数均可通过最小二乘法识别。

若忽略小参数ε的高次幂级数，则回归模型为

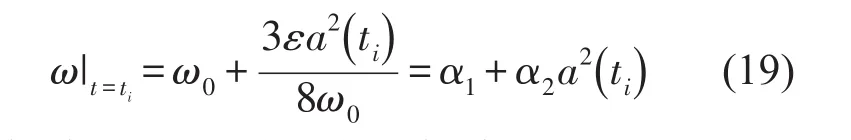
式中ω为响应信号的瞬时频率，而α1=ω0和为待求系数，且α1和α2分别与刚度k1和k2相关。联立式(19)中各个采样点ti(i=1,…n)的值，可得待求系数的矩阵形式

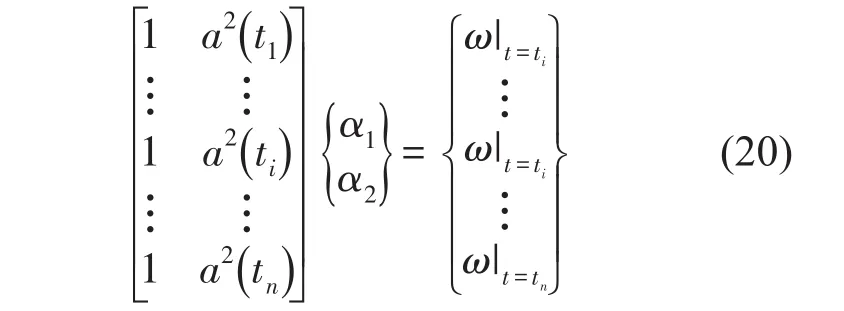
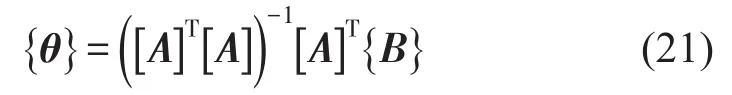
式中[∙]T和[∙]-1分别表示转置矩阵和逆矩阵。

然后根据待求系数α1、α2与刚度k1、k2的关系，可得Duffing非线性系统的刚度值为

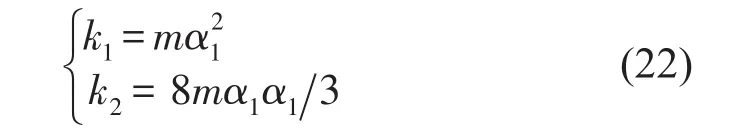
4 数值算例验证

Duffing方程是从简单物理模型中总结出来的非线性振动模型。土木工程结构中的许多非线性振动问题的数学模型都可以转化为该方程来研究。经典的Duffing非线性系统方程的表达式为

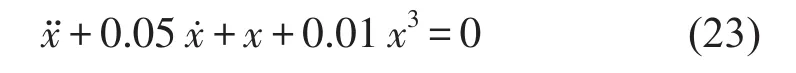
式中k1=1，k2=0.01，c=0.05，m=1，x，ẋ，ẍ分别表示系统的位移、速度和加速度。初值条件为x0=10，ẋ=0，采用4阶龙格-库塔法求解Duffing非线性系统的位移响应，时间间隔取0.1 s，时间总长取100 s。系统的位移响应及其幅值(虚线)如图2所示。

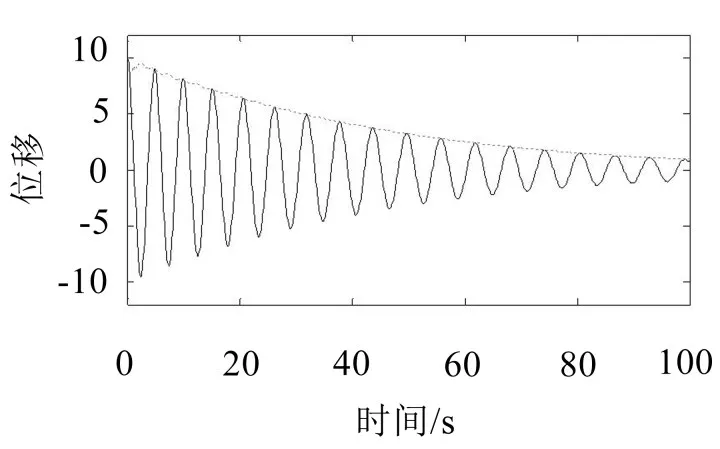
图2 Duffing非线性系统位移响应及幅值

采用复Morlet小波对Duffing非线性系统的位移响应进行连续小波变换，其小波量图如图3所示。

由图3可知，小波脊线较为模糊，且存在毛刺现象。但是从图3中我们可以确定搜索范围(虚线所示)并设定初始频率值为0.2 Hz，然后采用最大坡度法提取小波脊线，识别的瞬时频率如图4所示。

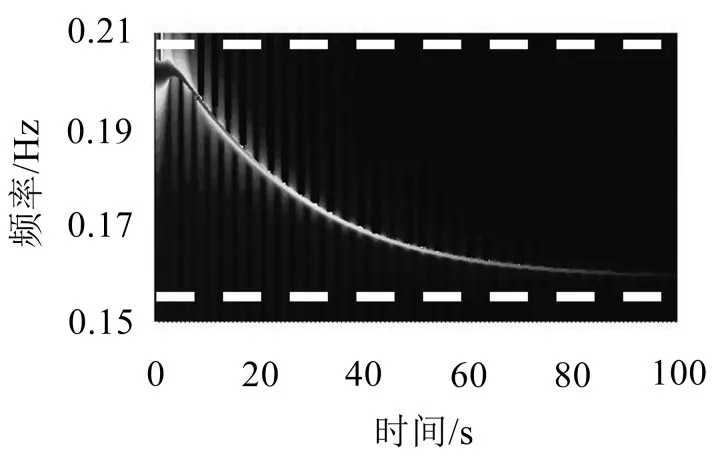
图3 Duffing非线性系统小波量图

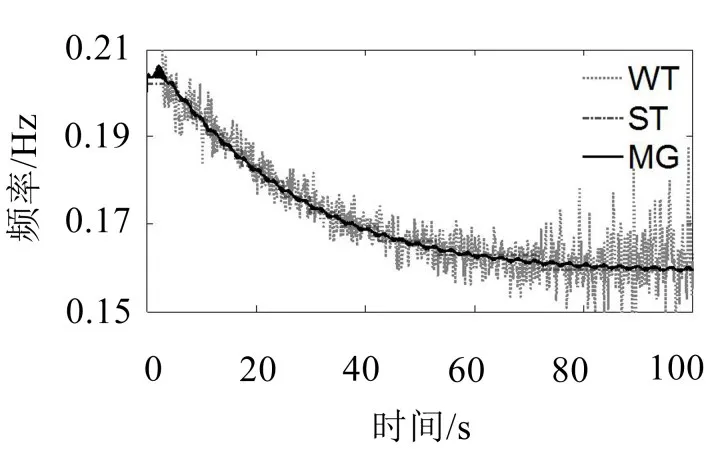
图4 基于最大坡度法的Duffing非线性系统位移响应瞬时频率识别结果

由图4可知，瞬时频率在自由振动的初始阶段急剧下降，然后逐渐变为线性，最后趋近于水平线。瞬时频率识别结果表明在初始阶段由于系统的位移较大，系统的非线性程度强，因而频率较高。随着系统响应的减弱，系统的频率也开始降低。当Duffing非线性系统响应趋近于零时，其频率约等于线性系统的频率0.16 Hz。为验证最大坡度法(MG)识别瞬时频率的准确性，在图4中同时给出了基于连续小波变换系数模局部极大值(WT)方法的瞬时频率识别值和基于同步挤压小波变换(ST)的瞬时频率识别值。由图4可知，基于连续小波变换系数模局部极大值识别的瞬时频率曲线出现了大量毛刺，其识别精度较差。而同步挤压小波变换只能处理信号在频率不变时尺度方向的扩散，即只提高时频曲线的频率精度，因此其瞬时频率曲线呈阶梯形。图4结果表明：基于最大坡度法的瞬时频率识别效果优于基于连续小波变换系数模局部极大值和同步挤压小波变换方法。

在成功提取非线性系统的瞬时特征参数之后，根据识别的瞬时频率和瞬时幅值可求得Duffing非线性系统的骨架曲线，而式(24)给出了具有立方体刚度的Duffing非线性系统理论骨架曲线[22]，其与最大坡度法(MG)、基于连续小波变换系数模局部极大值(WT)和同步挤压小波变换(ST)方法的骨架曲线识别比较结果如图5所示。

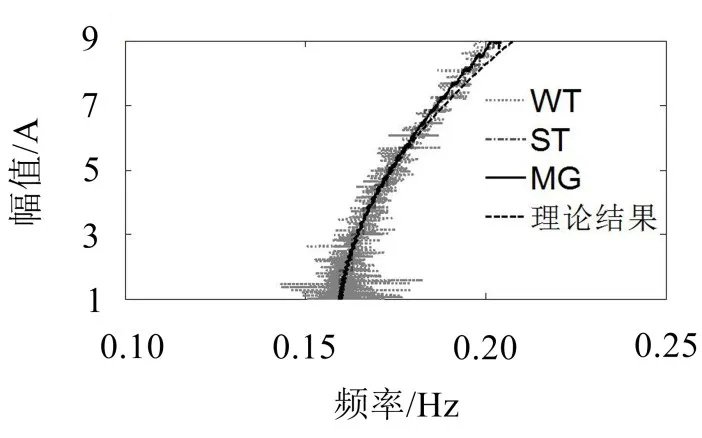
图5 Duffing非线性系统骨架曲线

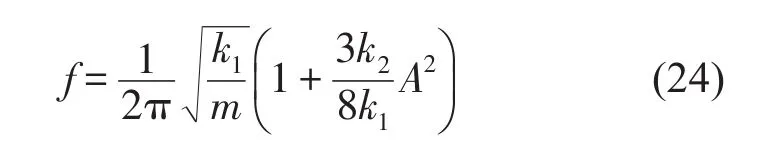
式中f、A分别为瞬时频率和瞬时幅值，k1，k2为刚度，m为质量。

由图5可知，本文方法构建的骨架曲线与理论结果基本吻合，且其值在理论结果附近振荡，因而能够很好地反映非线性系统的力学特性。基于连续小波变换系数模局部极大值(WT)得到的骨架曲线振荡得十分厉害，将直接影响到下一步的刚度识别结果。而同步挤压小波变换(ST)由于本身算法的局限性，其骨架曲线呈现阶梯形，且与理论值存在一定偏差。

根据式(20)和式(21)对识别的骨架曲线采用最小二乘估计算法，可得非线性系统的刚度系数k1，k2，如表1所示。为方便对比，表1同时给出了基于连续小波变换系数模局部极大值和同步挤压小波变换的刚度识别结果。由表1可知，采用最大坡度法得到的刚度k1，k2的识别值与真实值比较吻合，且线性刚度k1的识别效果要优于立方体刚度k2的识别效果。与基于连续小波变换系数模局部极大值方法和同步挤压小波变换方法相比，最大坡度法识别Duffing非线性系统的刚度效果最优。

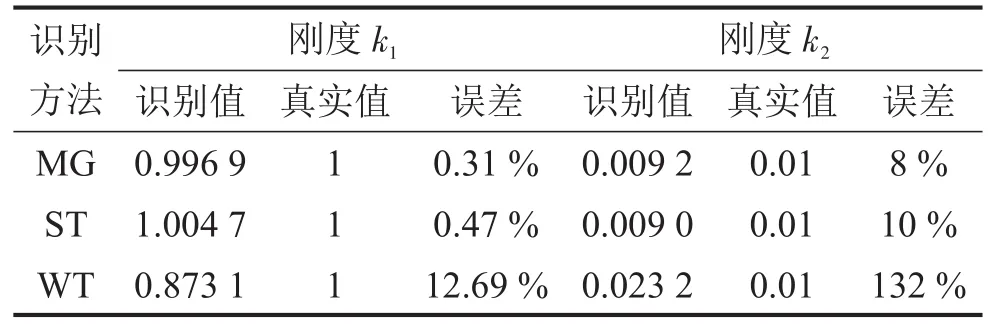
表1 最小二乘法识别的刚度

为考虑噪声的影响，对Duffing非线性系统位移响应分别施加5%、10%、15%和20%的高斯白噪声。噪声强度由信噪比(SNR)定义。

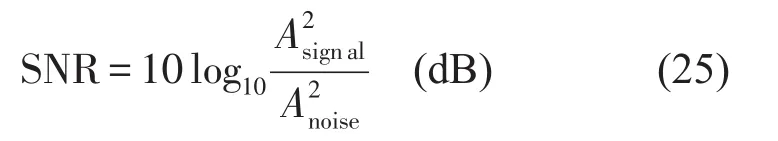
式中Asignal和Anoise分别为信号和噪声的均方根值，噪声水平是指的比值。例如取5%水平高斯白噪声时，SNR=13 dB。

根据上述识别流程，不同水平噪声下Duffing非线性系统的识别刚度如表2所示。

由表2可知，随着噪声水平的增加，最大坡度法识别的刚度误差虽然逐渐增大，但是与未添加噪声的识别值相差并不大。这说明本文提出的识别方法在噪声水平较大的情况下仍然能够有效识别结构的刚度参数，且精确度较高，因此该方法的抗噪性比较强。与基于连续小波变换系数模局部极大值方法和同步挤压小波变换方法相比，最大坡度法识别Duffing非线性系统刚度效果最优，同步挤压小波变换识别效果次之，而基于连续小波变换系数模局部极大值方法的识别效果则最差。

5 结语

鉴于非线性结构系统的频率和幅值随时间而变化，本文提出了一种新的识别Duffing非线性结构系统刚度的方法。首先建立Duffing非线性系统瞬时特性之间的关系式，然后通过最大坡度法和Hilbert变换分别提取了非线性结构系统响应的瞬时频率和瞬时幅值，最后通过最小二乘优化算法识别了非线性结构系统的刚度。通过一个Duffing非线性结构系统数值算例验证了所提出的方法，结果表明：该方法能够有效识别不同水平噪声干扰下Duffing非线性系统的刚度，且识别效果优于基于连续小波变换系数模局部极大值方法和同步挤压小波变换方法。

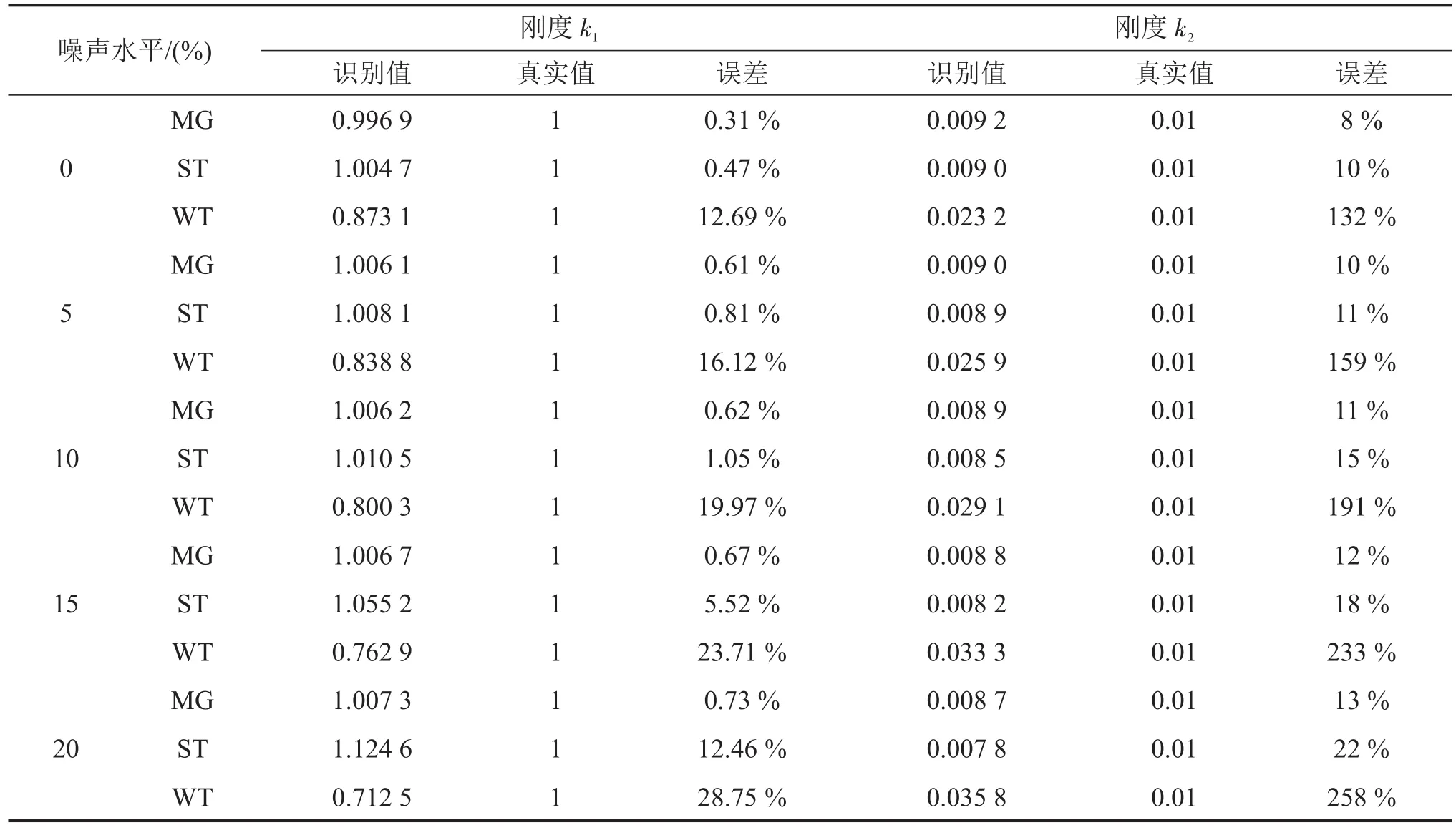
表2 不同噪声水平下识别的刚度

[1]黄东梅，周实，任伟新.基于小波变换的时变及典型非线性振动系统识别[J].振动与冲击，2013，33(13)：123-129.

[2]孙旭峰，胡超.脉动风作用下基于Hilbert-Huang变换的附加质量及气动阻尼识别[J].空气动力学学报，2015，33 (4)：542-547.

[3]FELDMAN M.Nonlinear system vibration analysis using the Hilbert transform-I.free vibration analysis method‘FREEVIB’[J].MechanicalSystemsandSignal Processing,1994,8:119-127.

[4]FELDMAN M.Nonlinear system vibration analysis using the Hilbert transforms-II.forced vibration analysis method‘FORCEVIB’[J].MechanicalSystemsandSignal Processing,1994,8:309-318.

[5]窦苏广，叶敏，张伟.基于增量谐波平衡的参激系统非线性识别法[J].力学学报，2010，42(2)：332-336.

[6]贾承林，黄方林，栾旭光.AR与Prony法的时变系统模态参数识别[J].噪声与振动控制，2009，29(1)：5-8.

[7]LEONTARITIS I J,BILLINGS S A.Input-output parametric models for nonlinear systems,partII: stochastic nonlinear systems[J].International Journal of Control,1985,41:329-344.

[8]VASTA M,ROBERTS JB.Stochasticparameter estimation of non-linear systems using only higher order spectra of the measured response[J].Journal of Sound and Vibration,1998,213(2):201-221.

[9]KERSEHEN G K,WORDEN K,VAKAKIS A F,et al. Past,present and future of nonlinear system identification in structuraldynamics[J].MechanicalSystemsand Signal Processing,2006,20:505-592.

[10]STASZEWSKI W J.Analysis of non-linear systems using wavelets[J].JournalofMechanicalEngineering Science,2000,214:1339-1353.

[11]STASZEWSKI W J.Identification of non-linear systems using multi-scale ridges and skeletons of the wavelet transform[J].Journal of Sound and Vibration,1998, 214:639-658.

[12]SHI Z Y,LAW S S.Identification of linear time-varying dynamical systems using Hilbert transform and empirical mode decomposition method[J].Journal of Applied Mechanics,2007,74:223-230.

[13]TJAHJOWIDODO T,AL-BENDER F,VAN BRUSSEL H.Experimental dynamic identification of backlash using skeleton methods[J].Mechanical Systems and Signal Processing,2007,21:959-972.

[14]YAN G,DE STEFANO A,OU G.A general nonlinear system identification method based upon time-varying trend of instantaneous frequencies and amplitudes[J].Advances in Structural Engineering,2012,15(5):781-792.

[15]邓杨，彭志科，杨扬，等.基于参数化时频分析的非线性振动系统参数辨识[J].力学学报，2013，45(6)：992-996.

[16]任宜春，易伟建.非线性系统识别的小波方法研究[J].振动与冲击，2007，26(3)：68-71.

[17]代煜，孙和义，李慧鹏，等.非线性系统识别的小波方法研究[J].振动与冲击，2009，28(2)：51-55.

[18]WANG C,REN W X,WANG Z C,et al.Instantaneous frequency identification of time-varying structures by continuous wavelet transform[J].Engineering Structures,2013,52:17-25.

[19]DAUBECHIES I,LU J,WU H T.Synchrosqueezed wavelet transforms:An empirical mode decompositionlike tool[J].Applied and Computational HarmonicAnalysis,2011,2(30):243-261.

[20]刘景良，任伟新，王佐才，等.基于同步挤压小波变换的结构瞬时频率识别[J].振动与冲击，2013，32(18)：37-42.

[21]刘延柱，陈立群.非线性振动[M].北京：高等教育出版社，2001：67-69.

[22]NAYFEH A H,MOOK D T,Nonlinear oscillations[M]. Wiley Interscience,New York,1979:62-71.

ANew Method for Stiffness Identification of Duffing Nonlinear Systems

LIU Jing-liang1,ZHENG Wen-ting2,HUANG Wen-jin1,HUANG Zhi-wei1
(1.School of Transportation and Civil Engineering,FujianAgriculture and Forestry University, Fuzhou 350002,China; 2.School of Civil Engineering,Fujian University of Technology,Fuzhou 350118,China)

The frequency variation of vibration responses of nonlinear vibration systems is closely related to the displacement,velocity and amplitude of the vibration,which is the main feature of the nonlinear vibration systems.In this paper,a new method for identifying the stiffness of Duffing nonlinear systems is presented based on this feature.First of all, the relation between instantaneous frequency and instantaneous amplitude of the Duffing nonlinear systems is established by means of Lindestedt-Poincaré method.Then,the maximum gradient method and Hilbert transform are employed respectively to extract the instantaneous frequency and the instantaneous amplitude from the nonlinear response signals.On this basis,the least square optimization algorithm is employed to identify the linear and cubic stiffness of the Duffing nonlinear systems.The effectiveness of the proposed new method is validated via a numerical example of a nonlinear Duffing system.The results demonstrate that the new method can identify the stiffness effectively even if the response signals are contaminated by Gauss white noise.

vibration and wave;Duffing nonlinear system;maximum gradient method;least square optimization algorithm;instantaneous frequency;instantaneous amplitude

P315.96；TU311.3

：A

：10.3969/j.issn.1006-1355.2017.03.014

1006-1355(2017)03-0072-06+106

2016-10-24

国家自然科学基金青年项目资助(51608122)；福建省自然科学基金青年科技人才创新项目资助(2016J05111)；福建农林大学青年教师科研基金项目资助(113-61201405104)

刘景良（1983－），男，湖南省衡阳市人，讲师，博士，研究方向为结构健康监测。E-mail:liujingliang@fafu.edu.cn