祖启航， 朱建青*， 宋传静

(1.苏州科技大学 数理学院， 江苏 苏州 215009； 2.南京理工大学 理学院， 江苏 南京 210094)

时间尺度上相空间中非Chetaev型非完整系统的Noether理论

祖启航1， 朱建青1*， 宋传静2

(1.苏州科技大学 数理学院， 江苏 苏州 215009； 2.南京理工大学 理学院， 江苏 南京 210094)

研究了时间尺度上相空间中非Chetaev型非完整力学系统的Noether理论.首先，基于Hamilton原理，建立了时间尺度上非Chetaev型非完整力学系统的Hamilton方程; 其次，根据时间尺度上Hamilton作用量在无限小变换下的广义准不变量，得到了时间尺度上相空间中非Chetaev型非完整力学系统的Noether等式和守恒量;最后，举例说明结果的应用．

时间尺度； 相空间； 非完整系统； Noether等式； 守恒量

1988年德国学者Hilger在他的博士论文[1]中提出测度链上的微积分理论，其主要思想就是把连续和离散进行统一[2-3].时间尺度作为测度链的一种特殊形式，非常具有代表性.目前，时间尺度在动态方程、变分原理、最优控制和经济等相关领域都得到了广泛的应用[4-11]．

近年来，国内外学者对时间尺度上力学系统的变分问题及其对称性与守恒量进行了研究.Bohner研究了时间尺度上Lagrange方程表达形式及变分问题[12]，Barosiewicz等研究了时间尺度上Lagrange系统的Noether理论[13]，Cai等研究了时间尺度上非保守和非完整力学系统的Noether理论[14]，Song和Zhang建立了时间尺度上Birkhoff方程，给出了Birkhoff系统的Noether等式与守恒量[15].本文基于时间尺度上Hamilton原理，建立了时间尺度上非Chetaev型非完整力学系统的Hamilton方程.根据Hamilton作用量在无限小变换下的准不变量，得到了系统的Noether定理．

1时间尺度上相空间中非Chetaev型非完整力学系统的运动方程

时间尺度上的微积分理论可参阅文献[6]．

(1)

(2)

时间尺度上Lagrange函数为

L=L(t，qσ(t)，qΔ(t))，

(3)

则有时间尺度上Lagrange非完整力学系统的微分方程[14]

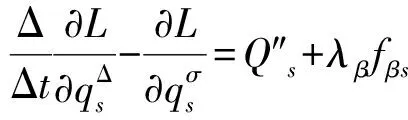
(4)

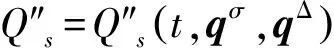
(5)

对约束条件(1)求Δ导数，并将方程(4)显示形式表示出来[7]

(6)

(7)

(8)

其中，

(9)

引进时间尺度上广义动量和Hamilton函数[9]

(10)

(11)

于是在正则变量p，qσ下，(1)、(2)和(9)式变为

(12)

(13)

(14)

时间尺度上非保守力学系统的Hamilton原理为

(15)

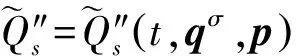
(16)

(17)

(18)

对(11)式两边关于广义动量求偏导数，得到

(19)

将(19)式代入(18)式，根据Dubois-Reymond定理[12]，可得

(20)

对(20)式求Δ导数，可得

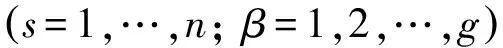
(21)

方程(19)和(21)称为时间尺度上相空间中非Chetaev型非完整力学系统的运动方程.由(14)式，方程(19)和(21)可进一步表示为

(22)

称方程(22)为与时间尺度上相空间中非完整系统(12)，(19)和(21)相应时间尺度上相空间中完整系统的运动方程．

2时间尺度上相空间中非Chetaev型非完整力学系统的Noether定理

首先，考虑只含有qs，ps变分的情况.相空间中Hamilton作用量表示为

(23)

定义1称作用量(23)式在变换

(24)

下为广义准对称不变量，当且仅当对任意区间[ta，tb]⊆[t1，t2],有

(25)

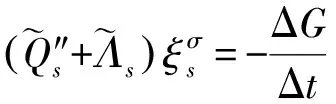
(26)

证明由定义1，方程(25)在任意区间[ta，tb]⊆[t1，t2]上均成立，则(25)式等价于

(27)

对(27)式两边同时关于ε求偏导数并令ε=0，则可以得到(26)式．

定理2如果作用量I是定义1下的广义准对称不变量，那么系统的守恒量为

C=psξs+G=const.

(28)

证明由(22)和(26)式，可得

(29)

于是得到(28)式.

下面将讨论含时间t的无限小变换下的广义准对称不变量．

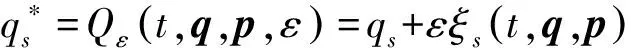
(30)

σ*∘α=α∘σ.

定义2如果作用量I是变换(30)式下的广义准对称不变量，当且仅当对任意的区间[ta，tb]⊆[t1，t2].

(31)

定理3如果作用量I是变换(30)式下的广义准对称不变量，那么

(32)

证明由定义2，可得

(33)

由于区间[ta，tb]是[t1，t2]的任意子区间，所以有

(34)

对(34)式两边同时关于ε求偏导数并令ε=0，则可得等式(32)．

(32)式就称为时间尺度上相空间中非Chetaev型非完整力学系统的Noether等式．

定理4如果作用量I是定义2下的广义准对称不变量，那么系统的守恒量为

(35)

证明令

(36)

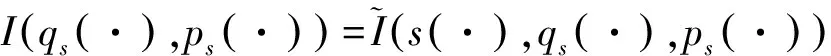
根据等式(33)有

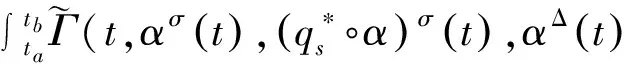
(37)

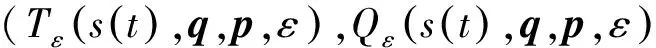
(38)

(39)

(40)

又因为

(41)

(42)

其中，∂1H表示对函数H中第一个变量求偏导数.将(41)、(42)式代入(40)式，则可得(35)式．

定理4称为时间尺度上相空间中非Chetaev型非完整系统的广义Noether定理，根据这个定理可由已知的广义准对称不变量得到系统的守恒量．

3算例

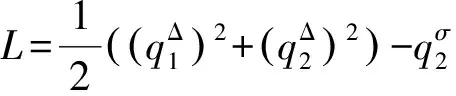
(43)

所受的非完整约束为

(44)

该约束为非Chetaev型的，虚位移满足

(45)

根据(10)式和(11)式，有广义动量和Hamilton函数

(46)

将Hamilton函数代入(21)式，则有

(47)

由(44)，(46)和(47)式，求得

(48)

于是有

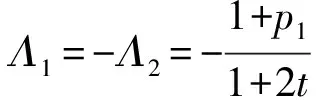
(49)

根据(32)式和(2)式，可得

(50)

(51)

对(50)和(51)式进行求解

ξ0=0，ξ1=1，ξ2=1，G=t，η1=η2=0，

(52)

所以根据定理4，可得到守恒量

C=p1+p2+t.

(53)

4结论

致谢：作者对张毅教授的悉心指导深表感谢!

[1]HILGERS.Einmaβkettenkalkulmitanwendungaufzentrumsmannigfaltigkeiten[D].Wurzburg:UniversitätWurzburg， 1988．

[2]HILGERS.Analysisonmeasurechains-aunifiedapproachtocontinuousanddiscretecalculus[J].ResultsMath， 1990， 18(1-2):18-56．

[3]HILGERS.Differentialanddifferencecalculus-unified[J].NonlinearAnal， 1997， 30(5):2683-2694．

[4]AGARWALRP，BOHNERM.Basiccalculusontimescalesandsomeofitsapplications[J].ResultsMath， 1999， 35(1-2):3-22．

[5]AGARWALRP，BOHNERM，PETERSONA.Inequalitiesontimescales:asurvey[J].JMathInequAppl， 2001， 4(4):535-557．

[6]BOHNERM，PETERSONA.Dynamicequationsontimescales，AnIntroductionwithapplications[M].Boston:Birkhäuser， 2001．

[7]BOHNERM，GUSEINOVGSH.Partialdifferentiationontimescales[J].DynSystAppl， 2004， 13(3): 351-379．

[8]ATICIFM，BILESDC，LEBEDINSKYA.Anapplicationoftimescalestoeconomics[J].MathComputModel， 2006， 43(7-8): 718-726．

[9]AHLBRANDDTCD，BOHNERM，RIEDNHOURJ.Hamiltoniansystemsontimescales[J].JMathApplAnal， 2000， 250(2): 561-578．

[10]HILSCHERR，ZEIDANV.Weakmaximumprincipleandaccessoryproblemforcontrolproblemsontimescales[J].NonlinearAnal， 2009， 70(9):3209-3226．

[12]BOHNERM.Calculusofvariationsontimescales[J].DynSystAppl， 2004， 13(12):339-349．

[13]BARTOSIEWICZZ，TORRESDFM.Noethertheoremontimescales[J].JMathAnalAppl， 2007， 342(2): 1220-1226．

[14]CAIPP，FUJL，GUOYX.Noethersymmetriesofthenonconservativeandnonholonomicsystemontimescales[J].SciChina:PhysMechAstron， 2013， 56(5):1017-1028．

[15]SONGCJ，ZHANGY.NoethertheoremforBirkhoffiansystemsontimescales[J].JMathPhys， 2015， 56(10): 102701(1-7)．

Noether theorem for nonholonomic systems ofnon-Chetaev’s type in phase space on time scales

ZU Qihang1， ZHU Jianqing1， SONG Chuanjing2

(1.College of Mathematics and Physics， Suzhou University of Science and Technology， Suzhou， Jiangsu 215009；2.College of Science， Nanjing University of Science and Technology， Nanjing 210094)

The Noether theorem for nonholonomic systems of non-Chetaev’s type in phase space is studied. Firstly， based on the principle of Hamilton， the Hamilton equations for nonholonomic mechanical system of non-Chetaev’s type on the time scale are established. Secondly， based on the generalized quasi invariance of the Hamilton action on time scale， the Noether identity and the conserved quantity of nonholonomic mechanical system of non-Chetaev’s type in the phase space on time scale are obtained. Finally， an example is presented to illustrate the application of the results．

time scale; phase space; nonholonomic systems; Noether identity； conserved quantity

2016-09-02.

国家自然科学基金项目(11572212)；苏州科技大学研究生科研创新计划项目(SKCX15_061).

1000-1190(2017)01-0023-05

O316

A

*通讯联系人.E-mail:zjq@mail.usts.edu.cn.