随机波动模型的首中时问题

2017-05-18张苗刘晖张飞龙

浙江大学学报（理学版） 2017年3期

张苗，刘晖，张飞龙

(1.西安电子科技大学数学与统计学院，陕西西安 710126； 2. 北京大学地球与空间科学学院，北京 100871； 3. 西安电子科技大学物理与光电工程学院，陕西西安 710126)

随机波动模型的首中时问题

张苗1，刘晖2，张飞龙3

研究了一类波动率是平方根过程的随机波动CEV模型的首中时问题.利用鞅方法求解首中时和波动率的联合拉普拉斯变换，继而将问题转换为求解一类变系数二阶常微分方程，通过变量代换将此方程转化为经典的Whittaker方程，得到联合拉普拉斯变换表达式.最后，选取不同的参数，使随机波动CEV模型的资产价格过程能够涵盖O-U过程、几何布朗运动、平方根过程等几种常见的扩散过程，画出不同参数下联合拉普拉斯变换函数的三维图像，并分析其变化趋势.

随机波动CEV模型;首中时;鞅方法;联合拉普拉斯变换;Whittaker方程

Journal of Zhejiang University(Science Edition), 2017,44(3):296-301

为了有效规避期权市场风险，BLACK等[1]提出了Black-Scholes期权定价模型(也称B-S模型).经典的B-S模型建立在波动率为常数这一假设基础之上，然而，大量研究表明，隐含波动率常呈现“微笑”的特征，这与B-S模型的基本假设相矛盾.为此，提出了随机波动模型[2-4].本文讨论的随机波动CEV(亦称常弹性方差)模型也是随机波动模型的一种，可用2个扩散方程描述，即资产价格过程和波动过程[5]，其中波动过程是平方根扩散过程，资产价格过程则涵盖了Ornstein-Uhlenbec过程(也称O-U过程)、几何布朗运动、平方根过程等几种常见的扩散过程.

近年来，首中时问题被广泛研究，MARIO[6]总结和推广了CARLSUND[7]的结论，得到布朗运动首中时的生成函数.文献[8-11]对O-U过程和反射O-U过程的首中时问题进行了研究.同时，文献[12]讨论了反射CEV模型的首中时问题，利用鞅方法计算得到首中时的拉普拉斯变换.以上研究均只针对单变量扩散过程，对随机波动CEV模型的双变量扩散过程首中时的研究却非常少.

本文借鉴单变量扩散过程首中时问题的求解方法——鞅方法[13-16]，在βcY+α=0这一假定条件下，将随机波动模型的首中时问题转化为求解一类变系数二阶常微分方程，通过变量代换[17-19]，将此方程转化为Whittaker方程，最终计算首中时和波动率的联合拉普拉斯变换.

1 随机波动CEV模型

尽管B-S期权定价模型的改进方法众多，但因随机波动模型独具优势，能够很好地描述时变波动，被广泛应用于建模利率期限结构和期权定价研究.

通常，随机波动模型描述成如下随机微分方程：

(1)

其中，Y=(Yt;t≥0)为随机波动因子，满足:

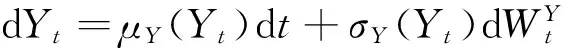
在常方差弹性过程中，方程(2)应为：

(3)

其中，φ(x)=aYxν，0≤ν≤1，系数aY为波动率的波动，ν为方差弹性.当ν=0.5时，为HESTON提出的均值回归过程；当ν=1时，为GARCH扩散过程.

本文主要考虑如下形式的随机波动CEV模型：

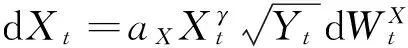
(4)

其中，γ≥0,aX>0,cY>0,bY≥0,aY>0.

2 首中时和随机波动因子的联合拉普拉斯变换

本节的目标是得到随机变量(Yτl,τl)的联合拉普拉斯变换表达式.对一个已知的首中阀值l∈R，定义随机波动模型的首中时如下：

τl=inf(t≥0;Xτl=l),

(5)

特别地，取infφ=∞.

通常情况下，由于很难得到随机变量(Yτl,τl)的联合分布表达式，因此可用联合拉普拉斯变换来代替.随机变量(Yτl,τl)的联合拉普拉斯变换定义如下：

φ(l;x,y)=Ex,y[exp(-ατl-βYτl)],

(6)

其中，E是期望算子且

Ex,y[·]=E[·|X0=x,Y0=y].

定理1 设非零函数f∈C2(R2)，R为实数，满足方程：

(7)

(8)

证明用鞅方法求解式(6)的解析表达式.首先，对f(x)∈C2(R2)应用It公式，得

定义：

那么M=(Mt;t≥0)是一个局部鞅.由分部积分公式，得：

因为函数f(x)满足方程(7)，并且βcY+α=0，则有

ρaXaYβxγf′(x)y-αf(x)=

这样

注意到Xτl=l，P-a.s.，于是令t→∞，

Ex,y[e-ατl-βYτlf(l)]=e-βyf(x).

可以证明

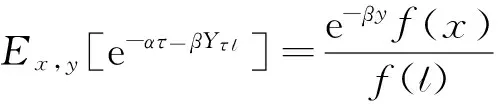
此时，只要知道方程(7)的通解f(x)，就可以得到随机变量(Yτl,τl)对应的联合拉普拉斯变换，因此，本文接下来的工作重点就是求解方程(7).

用变量代换法求解常微分方程(7).

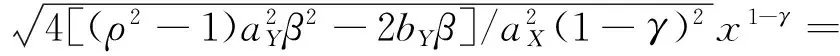
因为

代入方程(7)得

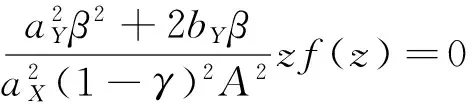
(9)

其中，

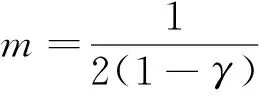
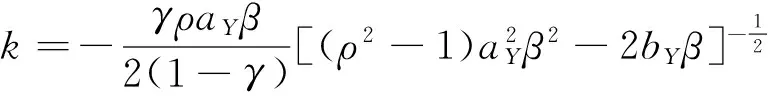
情况2γ=1，此时常微分方程(7)是欧拉方程，其通解为

f(x)=C1xλ1+C2xλ2,

其中λ1和λ2是常微分方程(7)的2个不相等的特征值.

将求出的通解f(x)代入定理1的式(8)，即有：

定理2 令(x,y)∈R×R+，R为实数，对满足条件βcY+α=0的(α,β)，随机变量(Yτl,τl)对应的联合拉普拉斯变换为

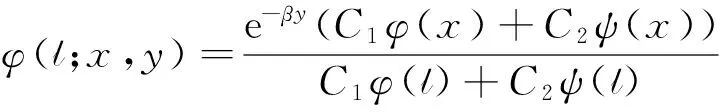
(10)

其中超几何函数φ(x)和ψ(x)定义为

同时，

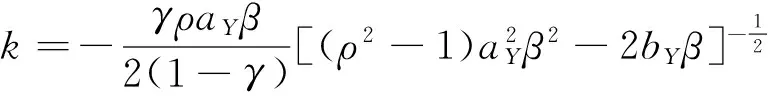
3 推论和结果分析

推论1 当γ=0时，令(x,y)∈R×R+，对任意满足条件βcY+α=0的(α,β)，随机变量(Yτl,τl)对应的联合拉普拉斯变换为

φ(l;x,y)=

其中,

φ(l;x,y)=

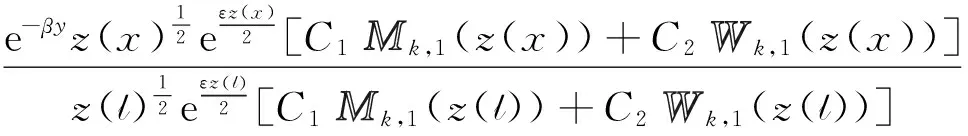
其中,

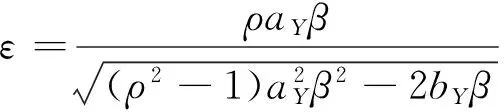
推论3 当γ=1，令(x,y)∈R×R+，对任意满足条件βcY+α=0的(α,β)，随机变量(Yτl,τl)对应的联合拉普拉斯变换为

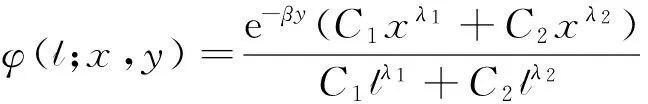
其中，λ1和λ2是常微分方程(7)的2个不相等的特征值.

利用这3个推论，分别画出当资产价格过程是O-U过程、平方根过程以及几何布朗运动时，联合拉普拉斯变化函数(x,y)→φ(l;x,y)的图像，并分析其变化趋势.

这里，取系数aX=1,aY=1,β=0.5以及首中阀值l=1，首先画出当γ=0，ρ分别取-1，0，0.5和1时，联合拉普拉斯变化函数(x,y)→φ(l;x,y).

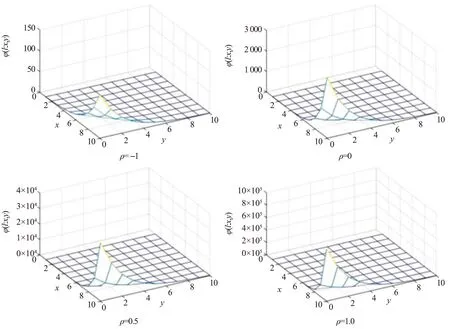
图1 当γ=0，联合拉普拉斯变化函数(x,y)→φ(l;x,y)Fig.1 The joint Laplace transform function (x,y)→φ(l;x,y) when γ=0

从图1可看出相关程度ρ和(Xt,Yt)初值(x,y)的选取对φ值的影响.首先，在不同相关程度ρ下，x取值越大，y取值越小,φ值就越大.随着相关程度的降低，φ值整体呈下降趋势.并且在不同相关程度ρ下，函数(x,y)→φ(l;x,y)的整体变化趋势基本相同.

图2 当，联合拉普拉斯变化函数(x,y)→φ(l;x,y)Fig.

图3 当γ=1，联合拉普拉斯变化函数(x,y)→φ(l;x,y)Fig.3 The joint Laplace transform function (x,y)→φ(l;x,y) when γ=1

4 结论

研究了一类波动率是平方根过程的随机波动CEV模型的首中时问题.利用鞅方法求解得到首中时和波动率的联合拉普拉斯变换表达式，并分析函数(x,y)→φ(l;x,y)在不同参数下的变化趋势.不足之处是，在给出拉普拉斯变换的显式表达式时，需有限定条件βcY+α=0.去除或弱化这一条件，使求解的拉普拉斯变换更为严格，这一问题有待进一步研究.

[1]BLACKF,SCHOLEM.Thepricingofoptionsandcorporateliabilities[J]. Journal of Political Economy,1973,81(3):133-155.

[2] HESTON S L. A closed-form solution for options with stochastic volatility with applications to bond and currency options[J]. The Review of Financial Studies,1993,6(2):327-343.

[3] HULL J,WHITE A. The pricing of options on assets with Stochastic volatility[J].Journal of Finance,1987,42(2):281-300.

[4] STEIN E, STEIN C. Stock price distributions with stochastic volatility: An analytic approach[J].Review of Financial Studies,1991(4):727-752.

[5] TALAMANCA G F. Testing volatility autocorrelation in the constant elasticity of variance stochastic volatility model[J]. Computational Statistics and Data Analysis,2009,53:2201-2218.

[6] MARIO L. First passage problems for asymmetric wiener processes[J]. Ecolepoly Technique de Montreal,2006,43(4):175-184.

[7] CARLSUND A. Cover Times, Sign-Dependent Random Walks, and Maxima[M]. Stockholm： Matematik,2003.

[8] BOROVKOV K, NOVIKOV A. On exit times of Levy-driven Ornstein-Uhlenbeck processes[J]. Statistics & Probability Letters,2007,78(12):1517-1525.

[9] PATIE P. On a martingale associated to generalized Ornstein-Uhlenbeck processes and an application to finance[J]. Stoch Process，2005,115:593-607.

[10] LOEFFEN R L, PATIE P. Absolute ruin in the Ornstein-Uhlenbeck type risk model[J]. Quantitative Finance,2010,arXiv:1006.2712.

[11] ALILI L, PATIE P, PEDERSEN J L. Representations of the first hitting time density of an Ornstein-Uhlenbeck process[J]. Stock Models,2005,21:967-980.

[12] BO L J, HAO C. First passage times of constant-elasticity-of-variance processes with two-sided reflecting barriers[J]. Journal of Applied Probability,2012,49(4):1119-1133.

[13] GERBER H U, YANG H L. Absolute ruin probabilities in a jump diffusion risk model with investment[J]. NAAJ,2007,1l(3):159-168.

[14] BO L J, REN G, WANG Y J. First passage times of reflected generalized Ornstein-Uhlenbeck processes [J]. Stochastics and Dynamics,2013,13(1):1250014.

[15] BO L J, WANG Y J. Some integral functionals of reflected SDEs and their applications in finance[J]. Quantitative Finance,2011,11(11):343-348.

[16] BO L J, TANG D, WANG Y J, et al. On the conditional default probability in a regulated market: A structural approach[J]. Quantitative Finance,2010,11(12):1695-1702.

[17] 冯海林，薄立军.随机过程——计算与应用[M].西安：西安电子科技大学出版社，2012. FENG H L，BO L J. Stochastic Process—Calculation and Application[M]. Xi’an:Xidian University Press,2012.

[18] 孙健.金融衍生品定价模型—数理金融引论[M].北京：中国经济出版社，2008. SUN J. Financial Derivatives Pricing Model-An Introduction to Mathematical Finance[M]. Beijing: China Economy Press,2008.

[19] 王高雄，周之铭.常微分方程[M].北京：高等教育出版社，2006. WANG G X, ZHOU Z M. Ordinary Differential Equations[M]. Beijing: Higher Education Press,2006.

The first hitting time of stochastic volatility models.

ZHANG Miao1, LIU Hui2, ZHANG Feilong3

(1.SchoolofMathematicsandStatistics,XidianUniversity,Xi’an710126,China； 2.SchoolofEarthandSpaceScienecs,PekingUniversity,Beijing100871,China； 3.SchoolofPhysicsandOptoelectronicEngineering,XidianUniversity,Xi’an710126,China)

This paper explores the first passage times of stochastic volatility CEV model. We mainly solve the joint Laplace transform of the first hitting time and volatility. Firstly, we use the Itformula to construct the martingale which can convert the problem into the process of solving a differential equation. Then, we introduce an appropriate second order variable coefficient ordinary differential equation, after a change of variable, it is turned to the Whittaker's equation. It’s not difficult to get the general solution of Whittaker’s equation. Thus, the explicit expressions for the joint Laplace transformation of the first passage times of stochastic volatility CEV model can be derived. Finally, selecting the parametersγbe 0, 1/2 and 1, let the asset price process covers the O-U process, geometric Brownian motion and square root process. Under different parameters, we obtain explicit expression of the joint Laplace transformation function, and use Matlab to draw the corresponding diagram and analyze the trend of graph.

stochastic volatility CEV model; first passage times; martingale method; joint Laplace transforms; Whittaker’s equation