☉江苏省苏州第十中学校 陈 蕾

数形结合在圆锥曲线中的应用

☉江苏省苏州第十中学校 陈 蕾

高考数学“考纲”明确地指出，高考不仅要对学生的基础知识、基础能力进行考核，还要加强学生的数学思想、数学思维的考查，而数形结合就是现阶段高中最重要的数学思想之一，几乎在每一套高考数学试卷中，都会出现对数形结合思想的考查.数形结合的考查方式也有很多，比如圆锥曲线、函数、三角函数、数列，还有线性规划，这些都可以考查学生对数形结合思想的掌握情况.在数学学习和解题过程中，要善于运用数形结合的方法来寻求解题途径，制定解题方案，养成数形结合的习惯，解题先想图，以图助解题.用好数形结合的方法，能起到事半功倍的效果，用一句话来形容就是，“数形结合千般好，数形分离万事休”.下面本文将介绍一下数形结合思想在圆锥曲线中几类常见题型中的应用.

一、直线和圆锥曲线的位置关系

计算Δ=64k2-4（m+4k2）（4-4m）.

令Δ≥0，可解得m≥1且m≠4.

解法2（数形结合解法）：根据直线l：y=kx+1的方程

评注：（1）解法1是学生通常能想到的解法，虽然想法很简单，但是解题的计算量很大，对于计算能力不强的同学来说，难度还是很大的.解法2的中心思想是利用图形本身的性质，如果直线和椭圆至少有一个交点的话，也就是说直线和椭圆一定是相切或者相交的，换句话说就是直线所过的定点一定要在椭圆上或者椭圆内.（2）如果直线中只含有一种参数，则直线一定经过定点，把含有参数的项合并在一起，然后令等式两端为零，即可得出所过定点坐标.

二、距离问题

例2如图1所示，M是抛物线y2=4x上的一个点，F是抛物线的焦点，∠MFx=60°，求|FM|.

解法1（普通解法）：因为∠MFx=60°，所以直线MF的斜率

图1

与抛物线方程联立可得一元二次方程3x2-10x+3=0，解得

所以可以最终确定M的坐标为（3，2■3）.

又|NH|=|GF|=2，

所以m=4，即|MF|=4.

图2

评注：（1）解法1是常规办法，根据直线的倾斜角得出直线的斜率，进而设出直线方程，通过联立解出M点的坐标，最后利用两点之间的距离公式来解出最后答案.此方法想法简单，一般同学都可以想到，但缺点是计算量较大，对于计算能力差的同学来说，不仅浪费时间，还不容易得出正确答案.（2）解法2利用数形结合，作垂线之后，形成一个特殊的直角三角形，利用图形本身的数量关系来解出所需要的|MF|值，此种解法虽然需要作辅助线，但是计算量极大简化，即使计算能力不好，也很容易得出正确答案，推荐同学们使用此种解法，在今后的学习中，要注意总结.

三、参数取值范围问题

例3已知直线l过点D（0，3），且与椭圆4x2+9y2=36交于不同两点M、N，设实数λ的取值范围.

解法1（普通解法）：如图3，设M（x1，y1），N（x2，y）2.

图3

当直线l的斜率不存在时，由于，且λ＜0，

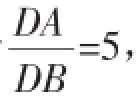
易知λ=-5或

当直线l的斜率存在时，设l：y=kx+3，联立方程

消去y，得（9k2+4）x2+54kx+45=0.①

由①得Δ=（54k）2-180（9k2+4）＞0，

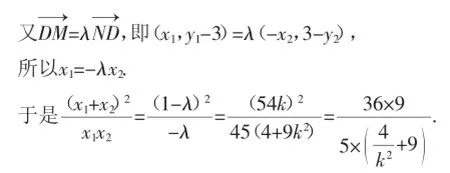
图4

因为直线l绕点D在直线l1和y轴之间旋转时，

数形结合的方法在高中数学的应用非常广泛，本文只是给出了在圆锥曲线题目中的几个应用，篇幅有限，还请广大数学同仁给予批评和指正.