何时浩

【摘 要】目标船舶航迹的动态行为分析对驾驶决策、交通管制、事故分析等有着很大的意义。利用matlab编程将AIS获取的经纬度信息转化成高斯平面直角坐标系信息，对转化后的数据运用软件编程进行最小二乘法的三次拟合能取得较好的效果。再结合船舶操纵运动方程对拟合的曲线进行分段拟合处理，提高精度，最后通过实验仿真进行检验。仿真结果表明，本文采取的算法能大大提高航迹复原的精确度，对船舶的动态行为分析起到了很大的帮助。

【关键词】最小二乘法；分段拟合；航迹复原

0 引言

随着各国海运业的发展，船舶密度的增加，船舶的安全问题就显得特别突出，实现高效的交通管制和事故分析就成为各国亟待解决的问题。准确地复原航迹线不仅对船舶的行驶状态有所了解，而且对出现事故的船舶也能做进一步地分析处理。

首先是对AIS获取的经纬度位置信息进行坐标的转换，变成平面直角坐标系信息，便于处理[1]；其次是先通过已知点推算临近时刻的数据点，增加拟合点的数量，然后运用基于最小二乘法的三次拟合算法并结合船舶操纵运动方程对拟合曲线进行分段处理，提高精度[2-3]；最后是结合实例，对本算法运用matlab软件编程进行仿真实验，验证其精确性。

1 数据转换

船舶航行时，通常用的是全球定位系统（GPS）获取实时信息，在研究船舶航迹过程中，常利用投影的办法将船舶空间数据转换为平面数据，从而可以在平面内绘制船舶航行轨迹。本文采用的是高斯-克吕格投影将经纬度信息转换为平面信息[4]。

1.1 GAUSS-KRUGER变换

在高斯-克吕格投影面上，赤道与中央子午线投影后都是一条直线，我们建立坐标系，以两者交点O作为坐标轴原点，纵坐标在这里称为x轴，对应于中央子午线的投影直线，横坐标为y轴，对应于赤道投影后的直线，这样就形成了高斯平面直角坐标系。

对于高斯-克吕格投影，椭球面上的一点映射到平面上的一点，计算公式用级数展开[5]；子午线弧长是椭球面上由赤道到投影点的距离，可由级数展开来计算。

1.2 数据预处理

导航定位的精度在数据测量方面是非常重要的。GPS本身的精度很高，但是在复杂的海况下受到气候、温度等因素的影响，另外还受到船身摇摆的幅度影响，这些都会影响接收机记录数据，难以精确测定船舶的航行轨迹。在利用GPS数据计算之前，首先须对接收来的大量信息进行分离提取、显示等环节的处理，这是保证海上地球物理调查数据质量的前提，主要有以下几个方面[6]：

1）获取的数据有很多无效数据，用滤波的方法剔除；2）将数据格式统一起来，方便后面调用；3）对检测出有整周跳变的数据点，需要查找并恢复这些跳变。

2 船舶回转运动和航迹的拟合

船舶在航行过程中，为了避让他船或躲避障碍物，需要通过操舵来改变舵角，从而改变航向。为了研究船舶的航迹拟合曲线和船舶回转运动，船舶操纵运动方程对分析轨迹起到了非常重要的作用。

2.1 船舶操纵运动方程

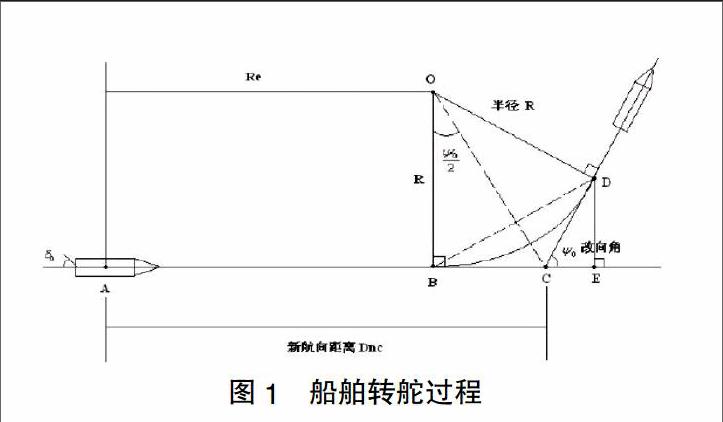
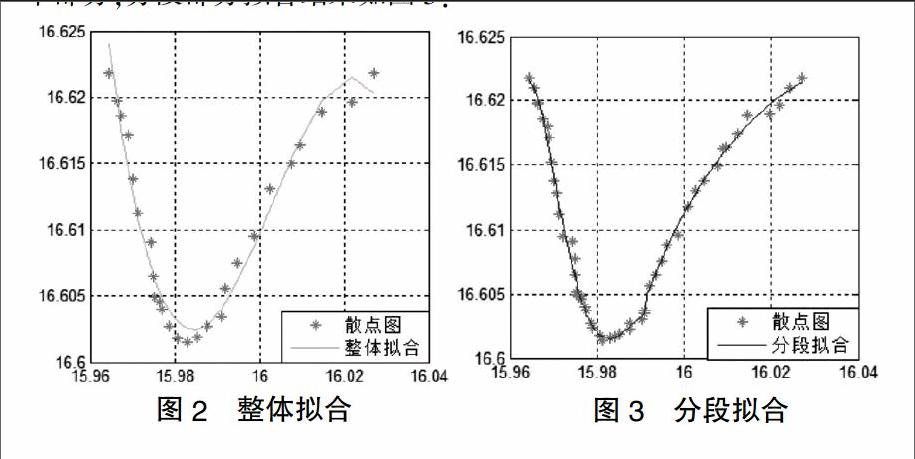
将船舶由操舵产生的各种运动变化看作输入，输出为运动变化响应关系，并且在分析Z型操纵实验的基础上得到了船舶操纵运动单状态变量线性方程：T■T■r+（T■+T■）r+r=K？啄+KT■？啄，其中T1，T2是船舶固有运动响应时间常数，在条件稳定的情况下T1，T2为正实数，且T1，<

该方程反映了船舶操舵角与转向角速度之间的关系，即船舶一阶操纵运动方程。式中r表示船舶转向角速度，r'表示船舶转向角加速度，？啄代表操舵角，K，T系数是船舶操纵性指数，分别表示船舶回转性指数和航向稳定性指数。

2.2 船舶回转运动

航行中的船舶在操舵后进行的运动我们称之为船舶回转性运动。船舶在回转运动过程中会有一个航迹线的变化过程，图1是船舶在操舵过程中的运动情况：

船舶在转舵过程中作曲线运动，我们将首向角改变弧度后的轨迹进行近似处理，看作是以R为半径的圆弧。根据船舶新航向距离，可以为船舶在何时何地施舵，确保船舶在现在所行的航道上准确地逐渐行驶到新的航道上，同时根据船舶新航向距离，以船舶回转运动开始及结束作为数据分段点，模拟船舶航迹。

2.3 航迹拟合

运用最小二乘法三次拟合算法进行航迹拟合得到的轨迹图误差相对较大。我们采取先后两种处理手段：第一，通过增加拟合点的数量来提高拟合的精确度；第二，采用分段曲线拟合的方法。结合上文中提到的船舶操纵方程，得出船舶转向角与舵角关系，并以转舵点为数据划分点，将数据分成若干段。为了保证最终的拟合效果达到最佳，该算法必须满足以下两点要求：1）为了确保拟合的曲线不出现间断点，必须保证分段函数每段的第一个点和最后一个点在拟合函数上；2）为了保证曲线的光滑性，要保证每段第一个点的导数值要和前一段最后一个点的导数值相等。

先设拟合曲线，求得它的近似值，再求它与实际值的差，可得到残差的平方和，通过对目标函数展开、转换，最终可以写成矩阵模式，从而转化为求最小值的问题。考虑到约束条件，对于第一段拟合函数的约束条件，只需考虑其连续性即可，对于中间段拟合函数，约束条件还要加上一个光滑性。

综上所述，原等式约束的最小二乘法问题被转化成一般形式的二次规划问题[7-8]，带入矩阵数据，根据二次规划计算公式以及利用matlab软件即可得到最优解。

3 仿真

通过AIS收集到的船舶经纬度信息，然后经转换算法转换到高斯平面直角坐标系中，进行实验仿真。具体思路如下，首先会对整体数据进行最小二乘法三次拟合处理，如图2，可以发现拟合的效果并不是很好，误差很大，所以接下来会进行增加拟合点数和分段拟合处理，再对每一部分进行最小二乘法三次拟合处理。根据上文提到的船舶操纵方程以及船舶转向角速度与舵角的关系，可以将这组数据分成三个部分，分段部分拟合结果如图3：

从图2、图3我们很明显可以看出，经增加拟合点数和分段处理后的拟合效果要比整体拟合效果好很多，所以本文采用的方法提高了航迹的精确性，更加接近与真实航迹，从而可以分析任意时刻船舶的动态行为。

4 结语

本文通过利用AIS收集到的船舶经纬度信息将处理后的数据进行分段拟合，采用基于最小二乘法三次拟合算法并结合船舶操纵方程及转向角速度与舵角之间的关系，将整体数据分为三段，分别进行拟合处理，并建立拟合模型。通过矩阵运算将拟合函数转化为二次规划问题，最后通过实验仿真验证其有效性。为了提高拟合精度，采取了增加已知点临近处的点迹作为已知拟合点，拟合结果表明，本文采用的方法明显提高了航迹复原的准确性，从而能够更加精确地进行船舶在任意时刻动态行為的分析。

【参考文献】

[1]赵森，许振宇，等.地理坐标与直角坐标相互转换的算法[J].火力与指挥控制，2001，26（4）：64-66.

[2]赵战兴.最小二乘法分段在船舶航迹拟合研究中的应用[J].舰船科学技术，2016，38（3）：85-87.

[3]张东林.分段最小二乘法曲线拟合[J].沈阳大学学报，1994（2）：80-83.

[4]刘健，刘高峰.高斯——克吕格投影下的坐标变换算法研究[J].计算机仿真，2005，22（10）：119-124.

[5]熊娟.内河船舶航迹拟合与模糊优化调度研究[D].武汉：武汉理工大学，2013.

[6]周保兴.GPS数据预处理方法研究及其应用[D].南京：河海大学，2005.

[7]张春.多项式曲线拟合的计算机解法及应用[J].西北水电屯，1993（3）：20-21.

[8]方曼，张尚剑，等.可用于舰船预测的多项式拟合方法及参数选择[J].舰船科学技术，2005，27（2）：24-26.

[责任编辑：田吉捷]