李 响，张浩东，王 桥，周 伟

(武汉大学水资源与水电工程科学国家重点实验室，武汉 430072)

0 引 言

边界元法[1]作为有限元法的一个重要补充，对于某些有限元法不能很好解决的问题具有先天的优势。边界元法只需要对求解问题的边界进行离散，将求解问题的维度降低一维，并且由于采用了求解问题的基本解，它是一种半解析半数值的计算方法，因此能得到较高的计算精度。对于裂纹扩展问题，边界元法只需要在裂纹尖端增加少量网格，极大地减少了工作量。对于一些复杂结构，例如含有细小孔洞的结构，含有细小水管的大坝结构和颗粒增强的复合材料结构等，采用边界元法只需要对构成其几何结构的边界进行离散，减少了网格划分的困难程度和计算自由度。由于采用了基本解，边界元法非常适用于求解无限域和半无限域的问题，使得其在岩土工程和地下结构工程中的应用前景非常巨大。

对于齐次方程，边界元法得到的积分方程只含有边界积分，然而，对于非齐次方程，即右端项不为零的方程，边界元法得到的积分方程除了含有边界积分外，还含有域积分。如果利用划分体网格的方法来计算域积分，边界元法便丧失了只对边界进行离散的巨大优势，因此边界元法不适合求解非线性问题。而实际工程中的问题最终提炼得到的方程往往是非齐次方程，例如力学问题一般都会考虑重力，这便极大地限制了边界元法在工程中的应用。

基于体网格的方法主要包括直接域积分法[2]，该方法需要对整个求解域进行离散，即需要划分体单元，导致边界类型算法失去了只对边界进行离散的这一主要优势。对于一些较为复杂的结构，体单元的划分也比较困难和耗时。

为了消除域积分需要的体网格，国内外很多学者提出了各种将域内积分转化为边界积分的方法[3]，常用的方法主要基于互易定理和散度定理。基于互易定理的方法主要包括双互易法和多互易法等。双互易法(dual reciprocity method, DRM)[4]是应用较为广泛的一种方法，在一些无网格法[5]和边界面法[6-8]中都有应用。该方法的基本思想是通过再一次的互易定理将域内积分转化为边界积分。为了达到这一目的，可以将控制方程的非齐次项采用一系列函数插值，常用的插值函数有径向基函(radial basic function, RBF)，需要在域内布置节点，在计算过程中往往需要先求解一个线性方程组，该线性方程组的系数矩阵一般是一个病态满阵，在布置的域内节点不均匀或者节点数量很多的情况下，可能导致求解结果的不稳定性[9-11]。

基于散度定理的方法是近年来才被提出的处理域积分的新方法，其具有代表性的方法为径向积分法(radial integration method, RIM)[12,13]，该方法最近得到了较为广泛的研究。该算法也是一种只需要对边界进行离散的方法，其基本思想是通过散度定理将域积分转化为包含一维径向积分的边界积分。该方法除了能够将域积分转化为边界积分之外，还能够非常有效的处理边界元法中的一些奇异积分。基于散度定理的方法还包括直线积分法(line integration method, LIM)[14]，该方法非常适合与快速多极算法结合求解大规模问题[15,16]。

本文拟提出一种新的域积分计算方法----自适应背景网格积分法。该方法将域积分近似为背景网格积分，只需要对边界进行单元离散，非常适合应用于边界元法中。数值算例表明，本文提出的方法具有较高的计算精度。本文将该方法应用于二维弹性力学问题，并对大坝结构进行了仿真计算，取得了较好的结果。

1 自适应背景网格积分法

1.1 自适应背景网格

在自适应背景网格积分法中，只需要将求解域的边界离散为边界单元，通过边界单元得到背景网格，在该过程中需要应用到二叉树结构。在详细介绍自适应背景网格的构造前，先定义如下参数：

网格大小：定义网格的大小为过正方形的边长；单元大小：定义单元大小为单元的长度；单元等级：初始单元的等级设为1，每个单元可以进一步细分为两个子单元，每个子单元的等级增加1，即等级为l+1的单元由等级为l的单元细分得到；预定义的最大网格大小：固定值，为事先定义的值来控制叶子网格的大小；预定义的最大单元等级：固定值，如果边界单元的等级大于该预定值，停止对该单元的进一步细分。

有了以上定义，构造自适应背景网格的主要步骤如下：

(1)将计算域离散为边界单元。边界单元可以直接采用边界元法中的单元。找到一个尽可能小的正方形覆盖求解域，该正方形为四叉树的根节点，称为根网格，所有的边界单元须在根网格之内。

(2)细分网格。将每个网格细分为4个相同大小的子正方形，称为子网格。如果父网格中的边界单元的部分或全部在子网格内，将该单元分配到该子网格内。每个单元可以同时在多个网格内(见图1)。

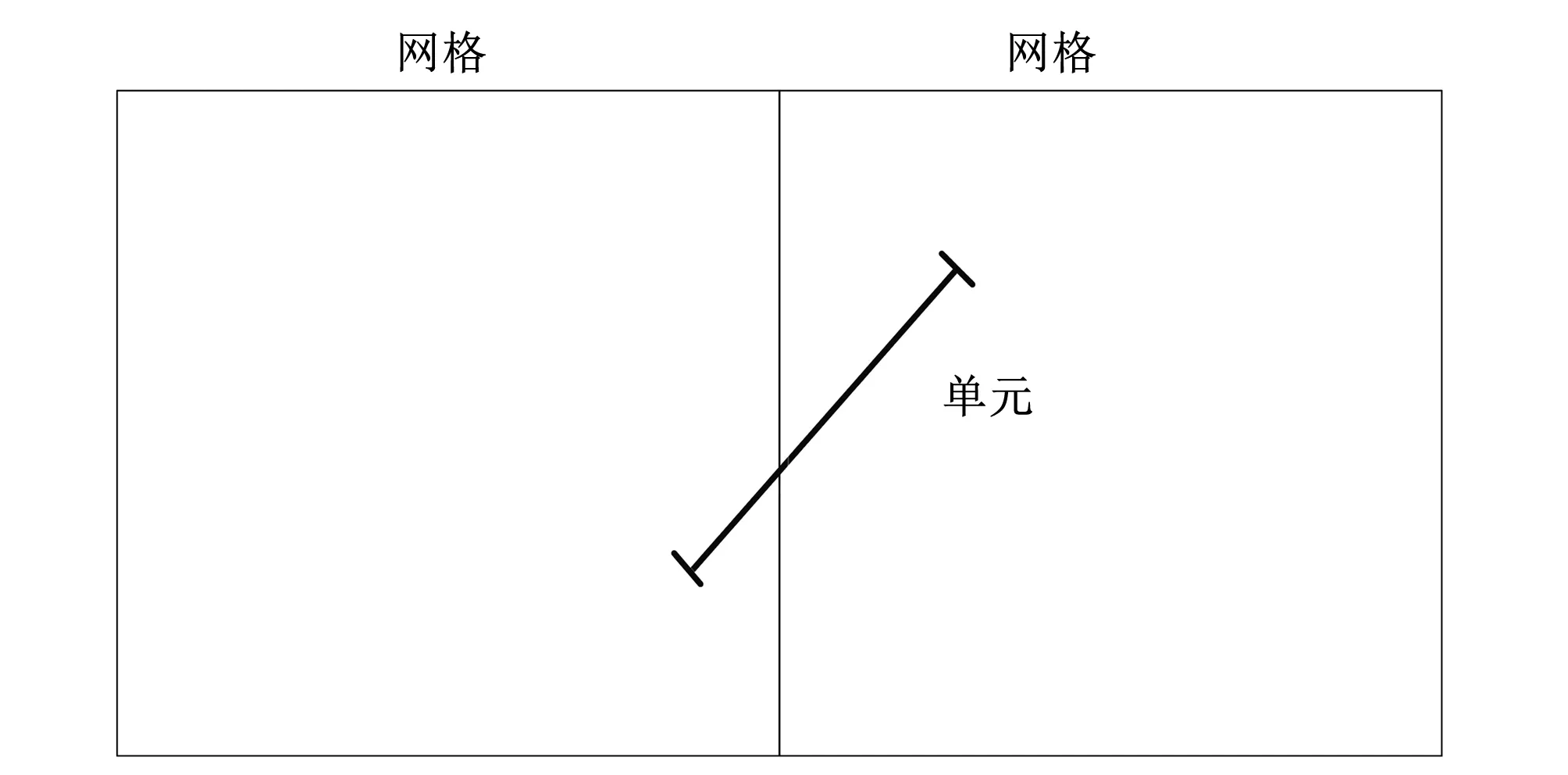
图1 一个单元在两个网格中Fig.1 A unit element in two grids

(3)重新细分网格或网格内的单元。首先得到每个网格内每个单元大小，如果单元的大小不比网格小，细分该单元并将每个新单元的等级增加1(图2)。重复该步骤，直到该网格内每个单元的大小均小于该网格的大小。如果单元的大小比网格大小的一半还小，回到第二步，即细分网格(图3)。该步骤可确保网格大小和该网格内的所有单元的大小较为接近。

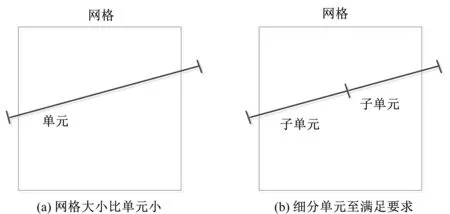
图2 细分单元Fig.2 Subdivision unit element

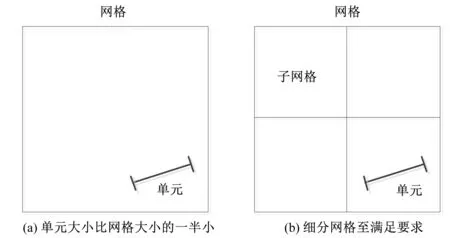
图3 细分网格Fig.3 Mesh refinement

(4)判断网格位置(见图4)。如果网格在计算域外，删掉该网格，如果在计算域内，进行(5)，否则，进行(6)。

(5)细分域内网格。如果域内网格大小大于域定义的最大网格大小，将该网格细分为四个相同大小的网格；重复该步骤直到网格大小小于域定义的最大网格大小。

(6)细分边界网格。如果该边界网格大小大于域定义的最大网格大小，回到(2)；否则，如果网格内单元的最小等级大于预定义的最大单元等级，停止细分，否则，回到(2)。

通过以上步骤即可构造基于边界单元的自适应背景网格，可以发现，该方法只需要边界单元的信息，区别于其他域积分方法。边界网格的大小通过边界单元的大小进行控制，边界单元大小越小或边界单元等级越高，得到的边界网格的大小便越小，而小的边界网格可以更好地接近原计算域。图4(b)是一个最终的网格细分例子。

图4 自适应背景网格构造过程Fig.4 Process of adaptive cell-based domain mesh

在(4)中，需要判断网格的位置。在该方法中，有3种网格：域外网格，边界网格和域内网格。如果网格中包含边界单元，称为边界网格，该类型的网格容易区分。域外网格和域内网格均不包含边界单元，区分较为困难，涉及点相对于几何体的位置问题。从以上步骤中，可以知道，在这种情况下该网格的父网格必然为边界网格，即其包含边界单元，通过这些边界单元，便可判断子网格在域内还是域外。在父网格内布置m个临时点，这些临时点分布于父网格内的边界单元上，那么可采用如下公式判断点x的位置：

(1)

式中：yi和ni为临时点的坐标和外法向量。

如果K>0，可认为x在域外，否则，可认为x在域内。

应用式(1)，在子网格中布置N个点(见图5)，于是可采用下式来判断网格的位置。

(2)

式中：xj为网格中的N个点。

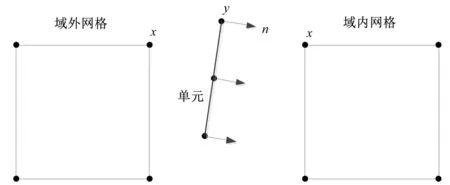
图5 子网格位置Fig.5 Sub-grid position

1.2 背景网格积分法

考虑如下二维问题中的域积分：

(3)

式中：Ω为积分域；f(y)为被积函数；y{y1,y2}为二维空间中的一点。

采用背景网格积分时，边界网格往往有一部分在域外，因此可定义如下新的方程：

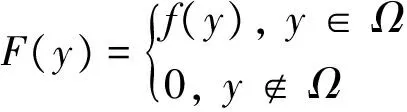
(4)

式(3)便可采用背景网格积分近似为：

(5)

式中：Ck为第k个叶子网格。

式(5)可采用高斯积分法计算。

2 边界元法求解包含体力的弹性力学问题

二维弹性力学问题的控制方程为如下几个方程：

σij,j+bi=0

(6)

(7)

σij=Cijklεkl

(8)

式中：σij为应力张量分量；bi为体力分量；εij为应变张量分量；ui为位移分量；ui,j为位移分量的导数。

i,j,k,l均为1到2，且：

Cijkl=λδijδkl+μ(δikδjl+δilδjk)

(9)

式中：μ为剪切模量；λ=2vμ/(1-2v)为拉梅常数，v是泊松比。于是可以得到如下求解弹性力学问题的正则化积分方程：

(10)

式中：x和y分别为场点和源点；u和t分别位移和面力张量；U(x,y)和T(x,y)为基本解，对于平面应变问题，有：

(11)

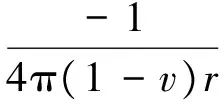
(1-2v)(rkni-rink)}

(12)

式中：r(x,y)为x和y之间的距离；n为边界上单位外法向量。

于是式(10)中的域积分可以写为：

(13)

其中：

(14)

3 边界元法在重力坝中的应用

本节给出了两个数值算例，验证了本文提出的方法的可行性和计算精度，并将该方法应用于重力坝的静力分析中，计算结果与有限元法进行了对比。

3.1 方法精度验证

该数值算例是一开孔的方板(图6)，其尺寸见图，采用无量纲单位，其体力为：

b1=ex2sinx1+ex2cosx1-

ex1sinx2-ex1cosx2

(15)

b2=ex1sinx2+ex2sinx1-

ex1cosx2-ex2cosx1

(16)

其中位移解析解为：

(17)

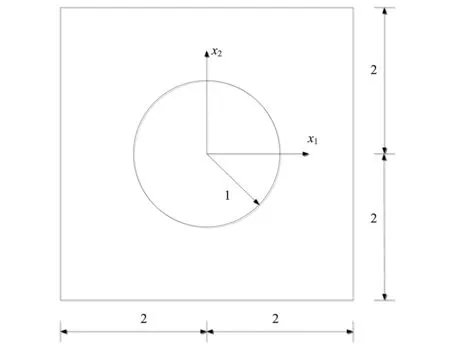
图6 圆孔方板Fig.6 Square plate with round hole

设该问题为平面应变问题，泊松比v=0.25，弹性模量E=1.0。外边界法向方向位移已知，切向方向和内边界面力已知，在边界上总共布置400个单元。图6和图7为以几何体中心为原点的极坐标下圆曲线r=1.5上的点的计算结果，横坐标为计算点与坐标原点组成的向量相对x轴的角度。从图中可以发现，计算结果与解析解吻合较好，具有较高的计算精度。

图7 圆孔方板的位移计算结果Fig.7 The displacement calculation results of Fquare plate with round hole

图8 圆孔方板的应力计算结果Fig.8 Stress calculation results of round hole square plate

3.2 重力坝计算

该算例考虑如图9所示的重力坝，其具体尺寸见图，单位为m，泊松比为v=0.2，弹性模量E=3.0 万MPa，大坝单位重量为25×103N/m3，左边水位高45 m，右边水位高13 m，水的单位重量为9.8×103N/m3，大坝底部完全约束。

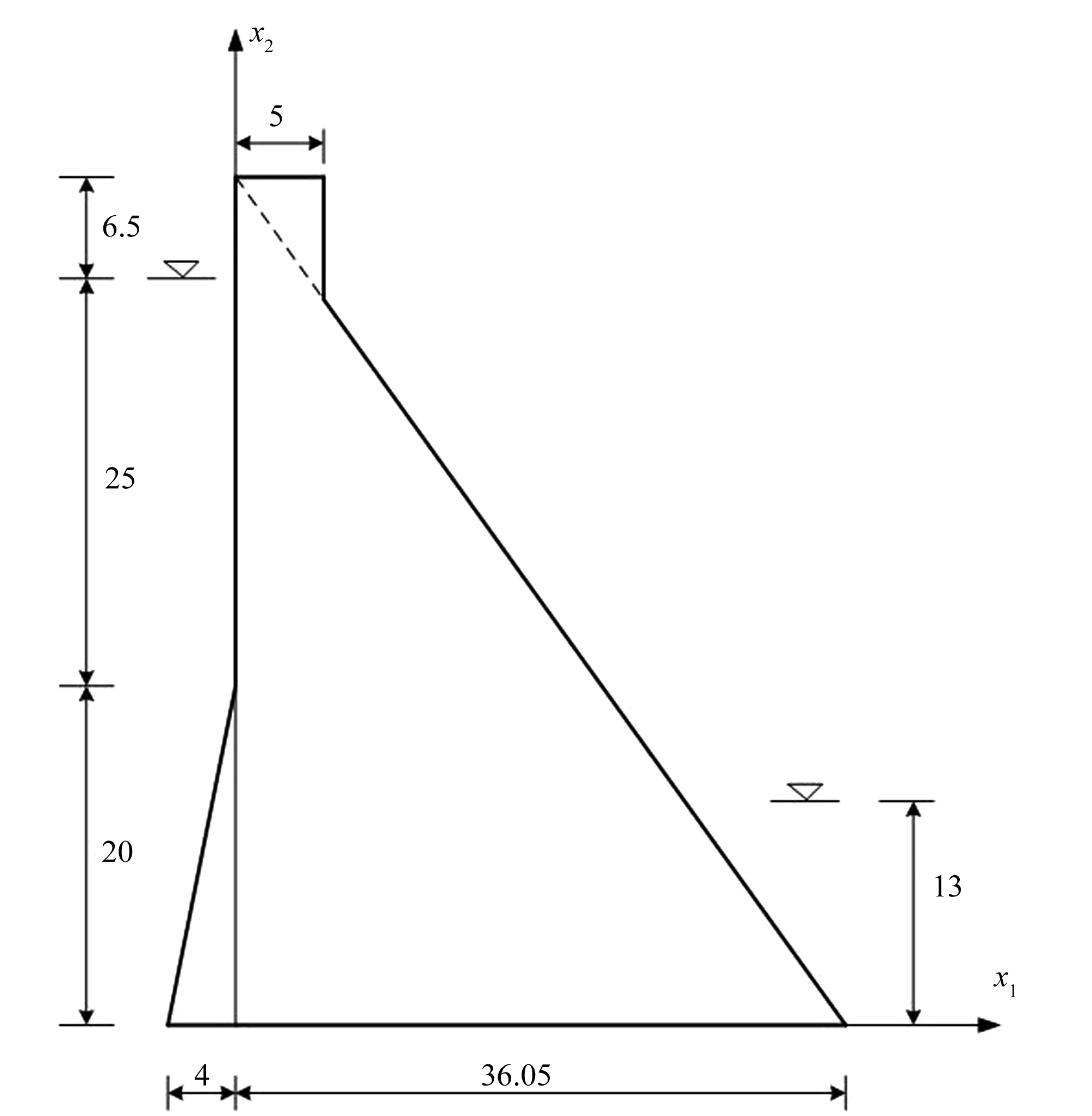
图9 重力坝模型(单位：m)Fig.9 Gravity dam model

该问题可采用平面应变问题求解。由于缺乏解析解，本文与有限元软件Abaqus的计算结果进行对比。图10和图11为直线x1=2.5上的位移u2应力σ2的计算结果，从图中可以看出，位移计算结果与有限元非常接近，应力计算结果本文方法只需要少量的边界单元便可得到较好的结果，而有限元法需要大量单元才能得到较好结果。

图10 重力坝位移计算结果Fig.10 The displacement calculation results of gravity dam model

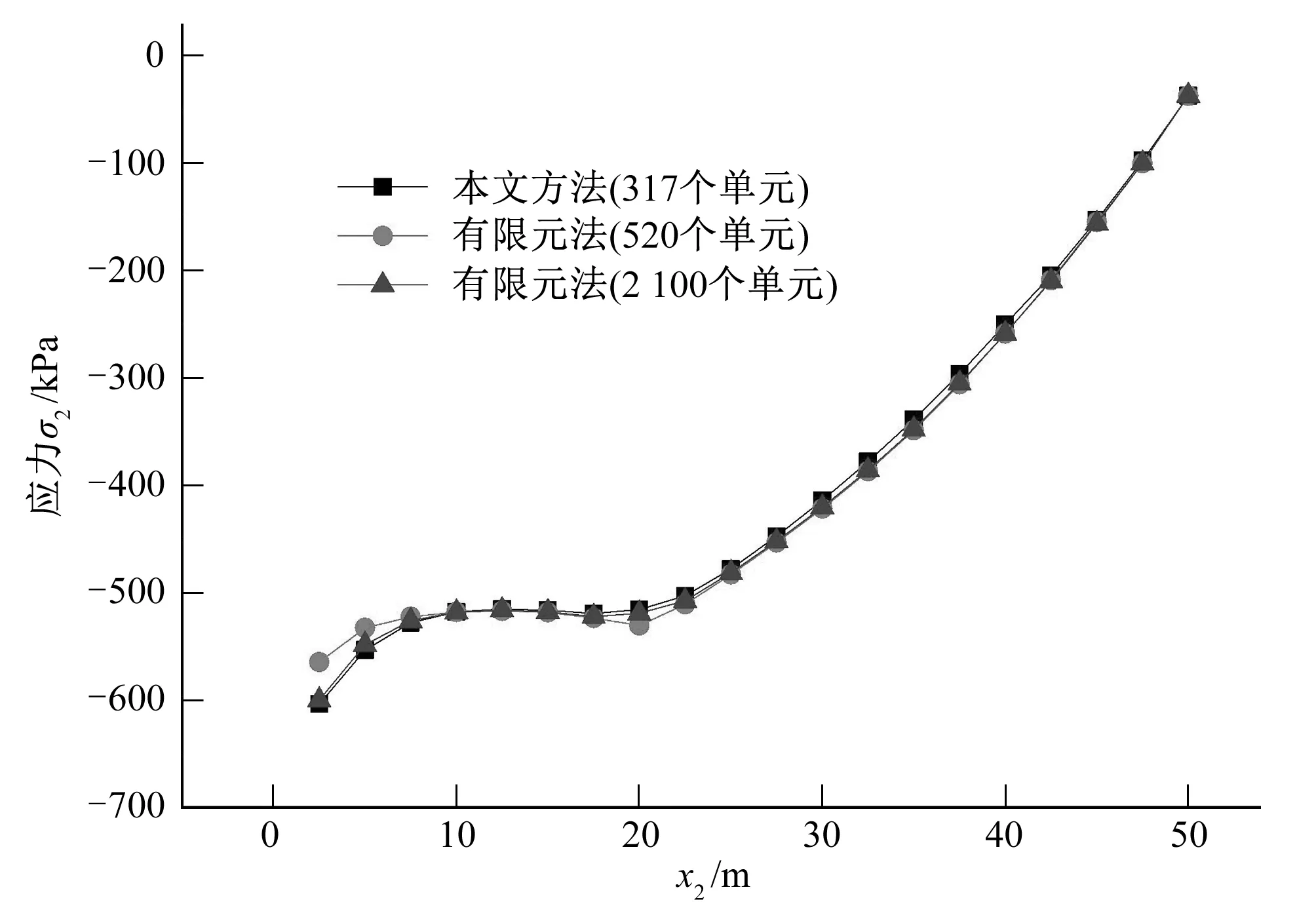
图11 重力坝应力计算结果Fig.11 Stress calculation results of gravity dam model

4 结 语

本文提出了一种边界元法中新的计算域积分的方法，称为自适应背景网格积分法。该方法只需要对边界进行单元离散，通过单元构造积分背景网格。在构造过程中需要引入树结构，对于二维问题为四叉树结构。本文将该方法应用于二维力学分析中，数值结果与解析解吻合较好。最后应用该方法对重力坝进行了仿真分析，并与有限元方法进行了对比，结果表明，本文的方法计算精度较高，采用较少的单元便可以获得较高的精度。

该方法的计算复杂度为O(NM)，其中N为计算节点数量，M为背景网格数量，因此对于大规模问题计算量较大。为了克服这一问题，可采用快速算法，例如快速多极算法进行加速，该内容正在研究过程中，成果将在后续工作中报道。

□

[1] 姚振汉,王海涛. 边界元法[M]. 北京:高等教育出版社, 2010.

[2] Dallner R, Kuhn G. Efficient evaluation of volume integrals in the boundary element method[J]. Computer Methods in Applied Mechanics & Engineering, 1993,109(1-2):95-109.

[3] Hsiao S C, Mammoli A A, Ingber M S. The evaluation of domain integrals in complex multiply-connected three-dimensional geometries for boundary element methods[J]. Computational Mechanics, 2003,32(4):226-233.

[4] Nardini D, Brebbia C A. A new approach to free vibration analysis using boundary elements[J]. Applied Mathematical Modelling, 1983,7(3):157-162.

[5] Miao Y, Wang Q, Liao B, et al. A Dual Hybrid Boundary Node Method for 2D Elastodynamics Problems[J]. Computer Modeling in Engineering & Sciences, 2009,53(1):1-22.

[6] Zhou F, Zhang J, Sheng X, et al. Shape variable radial basis function and its application in dual reciprocity boundary face method[J]. Engineering Analysis with Boundary Elements, 2011,35(2):244-252.

[7] Zhang J, Qin X, Han X, et al. A boundary face method for potential problems in three dimensions[J]. International Journal for Numerical Methods in Engineering, 2010,80(3):320-337.

[8] Zhou F, Zhang J, Sheng X, et al. A dual reciprocity boundary face method for 3D non-homogeneous elasticity problems[J]. Engineering Analysis with Boundary Elements, 2012, 6(9):1 301-1 310.

[9] Schaback R. Error estimates and condition numbers for radial basis function interpolation[J]. Advances in Computational Mathematics, 1995,3(3):251-264.

[10] Narcowich F J, Ward J D, Wndland H. Refined error estimates for radial basis function interpolation[J]. Constructive Approximation, 2003,19(4):541-564.

[11] Brownlee R A. Error estimates for interpolation of rough data using the scattered shifts of a radial basis function[J]. Numerical Algorithms, 2005,39(1):57-68.

[12] Gao X W. The radial integration method for evaluation of domain integrals with boundary-only discretization[J]. Engineering Analysis with Boundary Elements, 2002,26(10):905-916.

[13] Gao X W. Evaluation of regular and singular domain integrals with boundary-only discretization-theory and Fortran code[J]. Journal of Computational & Applied Mathematics, 2005,175(2):265-290.

[14] Wang Q, Zhou W, Cheng Y, et al. Line integration method for treatment of domain integrals in 3D boundary element method for potential and elasticity problems[J]. Engineering Analysis with Boundary Elements, 2017,75:1-11.

[15] Wang Q, Zhou W, Cheng Y, et al. A line integration method for the treatment of 3D domain integrals and accelerated by the fast multipole method in the BEM[J]. Computational Mechanics, 2016:1-14.

[16] Wang Q, Zhou W, Cheng Y, et al. The Boundary Element Method with a Fast Multipole Accelerated Integration Technique for 3D Elastostatic Problems with Arbitrary Body Forces[J]. Journal of Scientific Computing, 2016:1-27.