(Departmant of Applied Mathematics,School of Science,Northwestern Polytechnical University,Xi’an 710072,China)

§1.Introduction

LetG=(V(G),E(G))be a simple graph with vertex setV(G)and edge setE(G).Denote byv(G)the order ofGande(G)the size ofG,that is to say,v(G)=|V(G)|ande(G)=|E(G)|.ΓG(u)={v|uv∈E(G)}anddG(u)=|ΓG(u)|or simply Γ(u)andd(u),respectively.Letδ=δ(G)and∆ = ∆(G)denote the minimum degree and maximum degree of the graphGrespectively.LetXandYbe disjoint subsets ofV(G),respectively.e(X,Y)is the number of edges(inG)joining vertices inXto vertices inYforG.LetPn,Sn,CnandKnbe the path,star,cycle and complete graph of ordern,respectively.

The union ofG1andG2is the graphG1∪G2,whose vertex set isV1∪V2and whose edge set isE1∪E2.kGdenotes the union ofkcopies ofG.The join of graphsG1andG2is the graphG1∨G2obtained fromG1∪G2by joining each vertex ofG1with every vertex ofG2.Let=K1∨(kK2∪(n−2k−1)K1)(see Fig.1).We useUnto denote the family of all unicycles graphs of ordernandBnto denote the family of all bicyclic graphs of ordern.

The matrixQ(G)=D(G)+A(G)is called the signless Laplacian matrix ofG,whereA(G)is the adjacency matrix ofGandD(G)is the diagonal matrix of vertex degrees ofG.The matrixL(G)=D(G)−A(G)is called the Laplacian matrix ofG.The largest eigenvalue ofA(G),L(G)andQ(G)are called the spectral radius,Laplacian spectral radius and signless Laplacian spectral radius(orQ-index)ofG,respectively and denoted byρ(G),µ(G)andq(G),respectively.The study of the spectral properties has attracted much attention and the reader may consult[3-4,15-17].

The central problem of the classical extremal graph theory is the Tur´an’s Problem:

Problem AGiven a graphF,what is the maximum number of edges of a graph of ordern,with no subgraph isomorphic toF?

Such problems are well understood nowadays,for example,see the book[2]and the survey[12].Recently,Nikiforov,et al,investigated spectral Tur´an’s Problem,namely for the spectral radiusρ(G)of a graphG.In this new class of problems the central question is the following one.

Problem BGiven a graphF,what is the maximum spectral radiusρ(G)of a graphGof ordern,with no subgraph isomorphic toF?

In[12],when the graphFis the complete graphKr,the path or the cycle etc.,Nikiforov determines the largest spectral radius of the graphGand their corresponding extremal graphs.The present paper contributes to an even newer trend in extremal graph theory,namely to the study of variations of Problem A for the signless Laplacian spectral radius of graphs,where the central question is the following one.

Problem CGiven a graphF,what is the maximum signless Laplacian spectral radiusq(G)of a graphGof ordern,with no subgraph isomorphic toF?

In[6],Nikiforov et al.determine the maximum signless Laplacian spectral radius of graphs with no 4-cycle and 5-cycle.And when the graphFis the complete graphKr,the path or the cycle etc.,the authors in[1,13-14,18]determine the largest signless Laplacian spectral radius of the graphGand their corresponding extremal graphs,respectively.He and Guo in[9]determine the extremal graph of the signless Laplacian and Laplacian spectral radius amongC3-freek-cyclic graphs of ordern.

In this paper,we determine the maximal signless Laplacian spectral radius ofC4-freekcyclic graphs of ordernand characterize its extremal graph.Furthermore,we determine the first three signless Laplacian spectral radii ofC4-free unicycles graphs of ordernandC4-free bicyclic graphs of ordern,respectively.

§2.Main Lemmas

In this section,we state some well-known results which will be used in this paper.

Lemma 1[10]LetGbe a connected graph of ordernandq(G)its signless Laplacian spectral radius ofG.Letu,vbe two vertices ofGandd(v)be the degree of vertexv.Assumev1,v2,···,vs(1≤s≤d(v))are some vertices of Γ(v)Γ(u)andX=(x1,x2,···,xn)Tis the Perron vector ofQ(G),wherexicorresponds to the vertexvi(1≤i≤n).LetG∗be the graph obtained fromGby deleting the edgesvviand adding the edgesuvi(1≤i≤s),Ifxu≥xv,thenq(G)＜q(G∗).

Lemma 2[5,11]For every graphG,we have

IfGis connected,equality holds if and only ifGis regular or semiregular bipartite.

Lemma 3[8,3]LetGbe a simple connected graph onnvertices with maximum degree∆and at least one edge.Then

where the former equality holds if and only if∆(G)=n−1 and the latter one holds if and only ifGis the starSn.

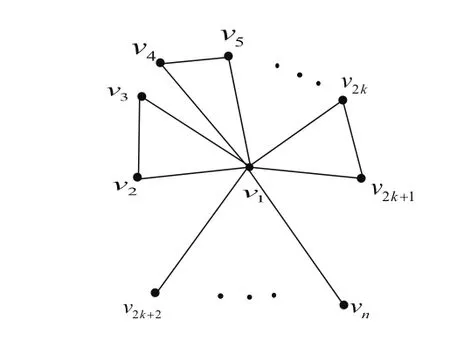
Fig.1 The k-cyclic Graph

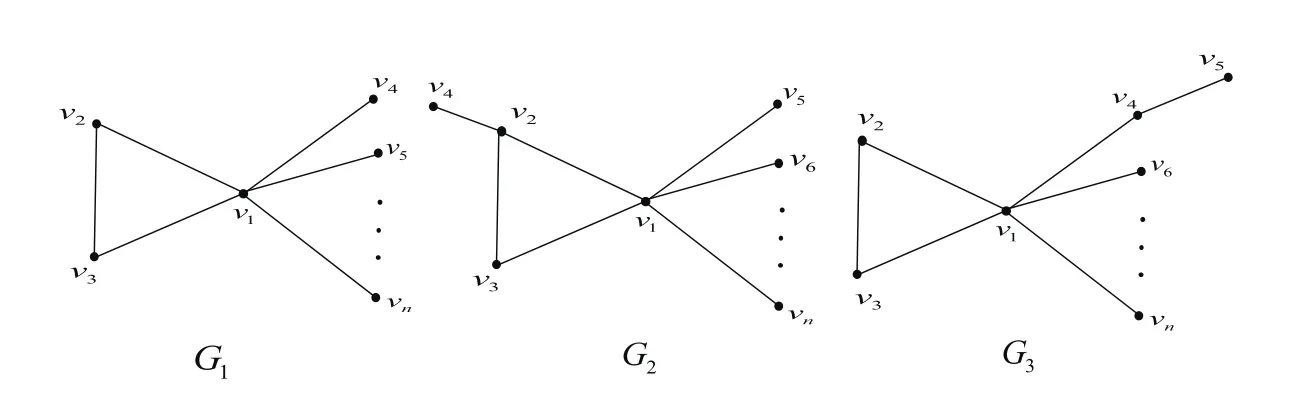
Fig.2 The First Three Unicycles Graphs

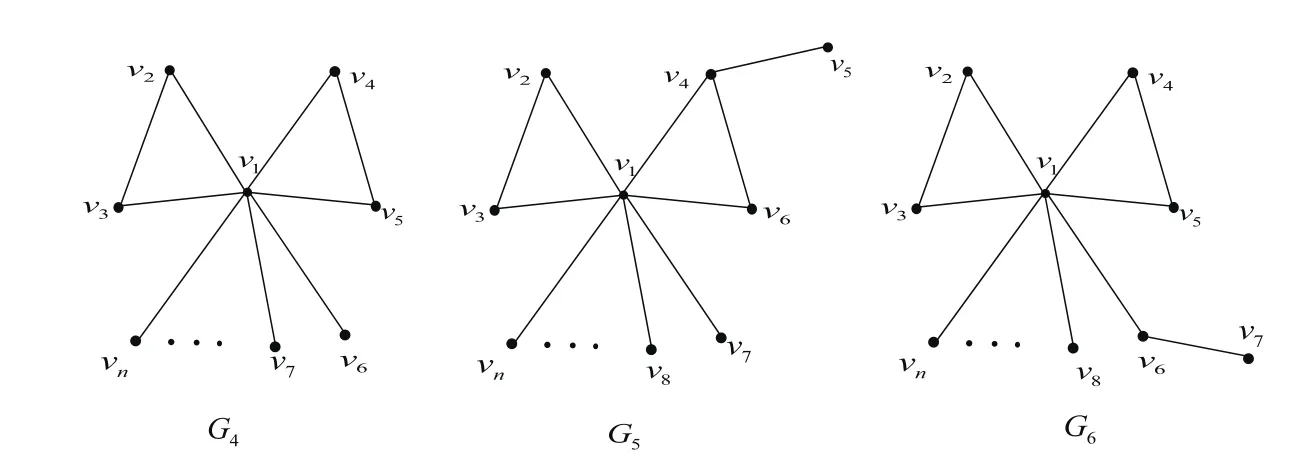
Fig.3 The First Three Bicyclic Graphs

Lemma 4Let2andG3be the graphs shown in Fig.1 and Fig.2.Then,q(G2)andq(G3)are the largest roots of the following equations,respectively,

ProofLetV={v1,v2,···,vn}andX=(x1,x2,···,xn)Tbe a Perron vector corrosponding toq).By the symmetry of,we have

Letq=q,from the eigne equations forQ,we see that

SinceX=(x1,x2,···,xn)Tis an eigenvector corresponding toq,soX/=0.Then

Soqis the largest root of the following equation

Consequently,qis the largest root of the following equation

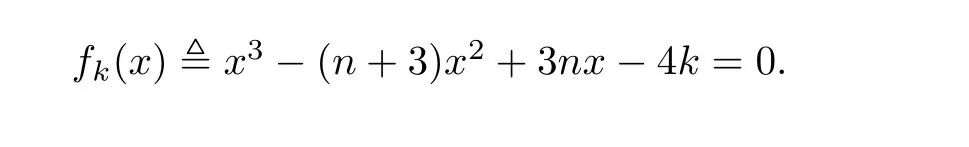
Using the same method,we obtainq(G2)andq(G3)are the largest roots of the following equations,respectively,

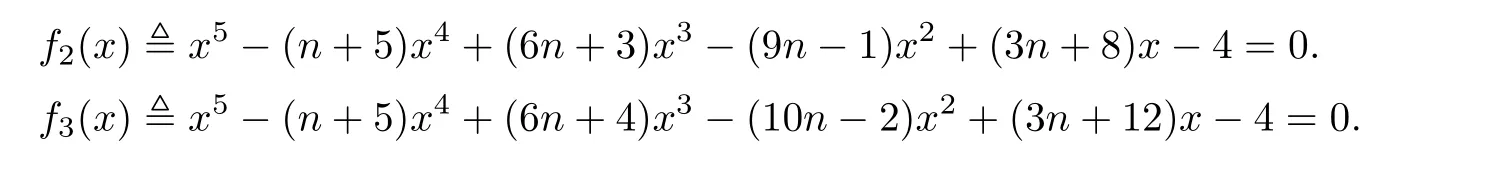
This completes the proof.

§3.Main Results

LetGbe aC4-freek-cyclic graph of ordern.Ifk=0 thenGis a tree.In[6,15],the authors determined the first eight Laplacian spectral radius of trees of ordern.For a bipartite graphG,by[3],we know thatL(G)andQ(G)have the same eigenvalues.A tree is a bipartite graph,so the results that are obtained by[6,15]hold also for the singles Laplacian spectral radius of trees of ordern.Therefore,in what follows,assume thatk≥1.

Theorem 5Letk≥1,n≥2k+2 and letGbe aC4-freek-cyclic graph of ordern.Then

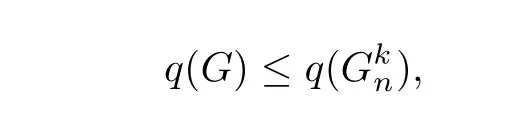
with equality if and only ifG=,whereqs the largest root of the equation

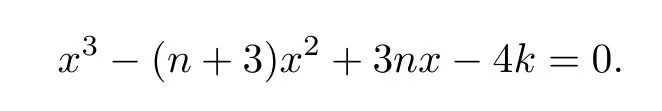
ProofBy Lemma 3,we have

Sincen≥2k+2 andGis aC4-freek-cyclic graph of ordern,we have∆(G)≤n−1.If∆(G)=n−1,it is easy to see thatGmust be.IfG/=then∆(G)≤n−2.By Lemma 2,letwbe a vertex ofGsuch that

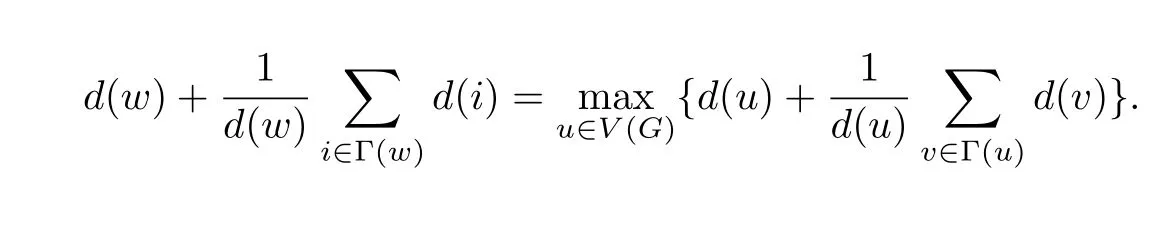
Then

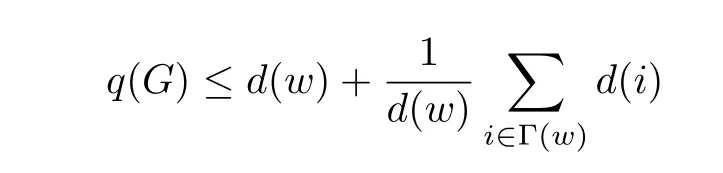
and 1≤d(w)≤∆(G)≤n−2.

If 2≤d(w)≤n−2,sinceGisC4-free,every vertexv∈V(G)Γ(w)has at most one neighbor in Γ(w).Then we have

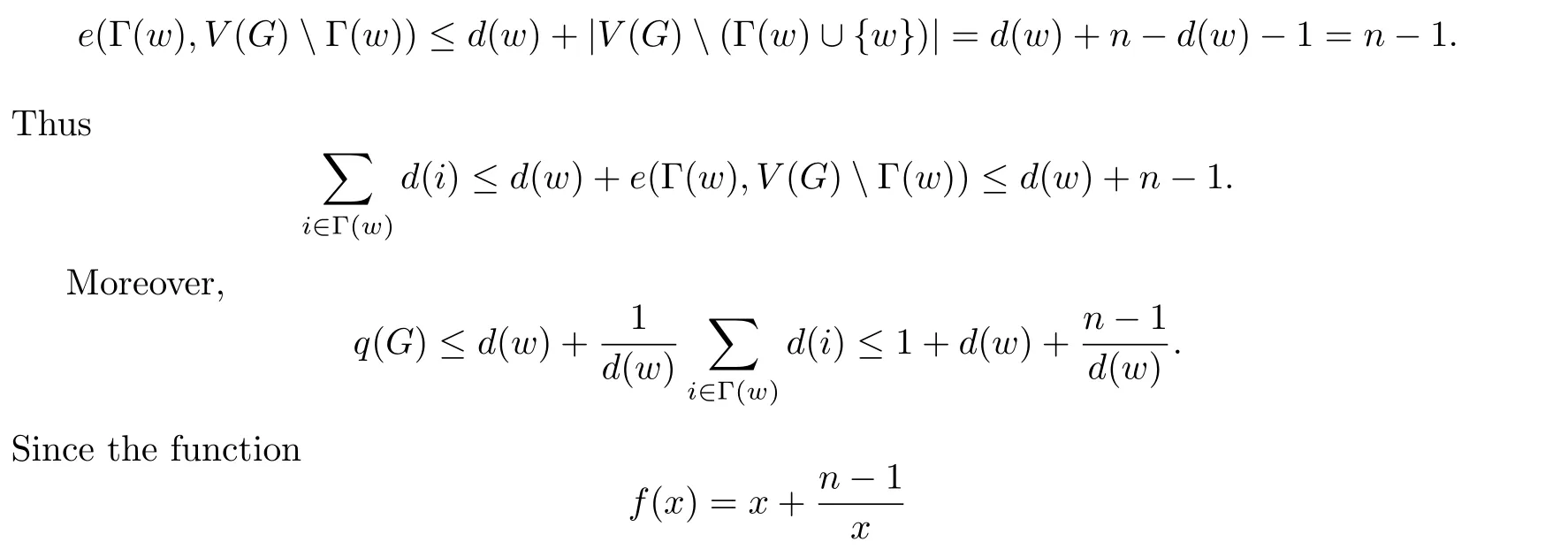
is convex forx＞0,its maximum in any closed interval is attained at one of the ends of this interval.If 2≤d(w)≤n−2,then

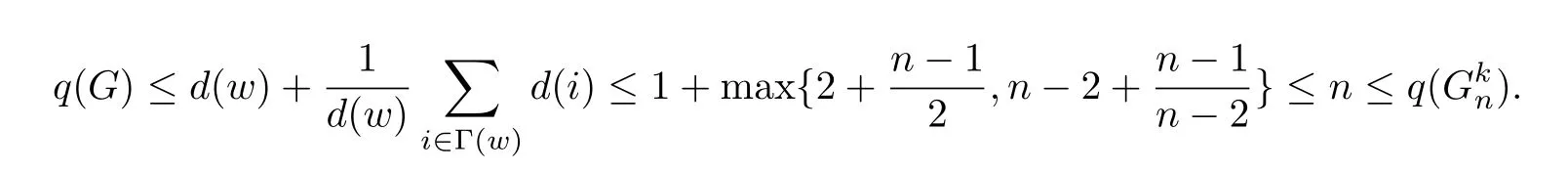
From the above all,we obtainq(G)≤q,with equality if and only ifG=.Then from Lemma 4,we know thatqis the largest root of the polynomial

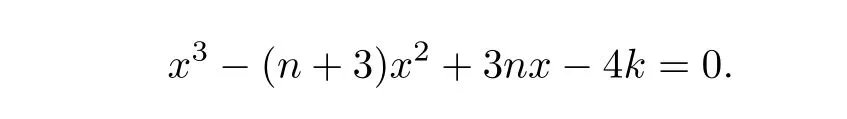
This completes the proof.

Theorem 6LetUnbe the set of all unicyclic graphs of ordernandn≥6,Gi∈Unfori=1,2,3.Then for anyG∈UnandG/=Gi(i=1,2,3),we have

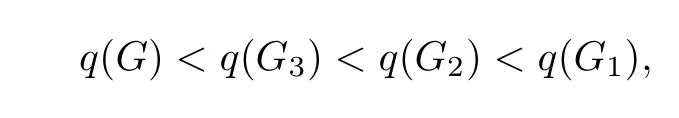
whereG1,G2andG3are the graphs shown in Fig.2.

ProofFor anyG∈Un,from Theorem 1,ifG/=G1,thenq(G)＜q(G1).Especially,q(Gj)＜q(G1)forj=2,3.Obviously,G2andG3are all the unicycles graphs with∆=n−2 inUn.Then for anyG∈Un,ifG/=Gi(i=1,2,3),then∆(G)≤n−3.By Lemma 3,q(Gj)＞∆(Gj)+1=n−2+1=n−1 forj=2,3.From Lemma 2,

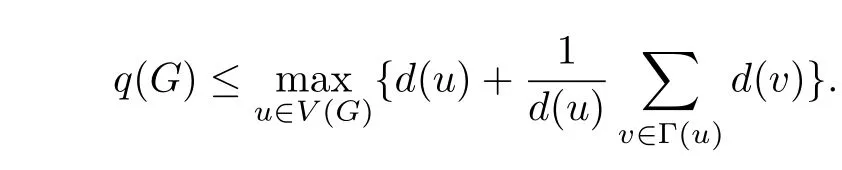
Similar to the proof of Theorem 1,we can getq(G)≤n−1＜q(Gi).

From Lemma 4,whenx≥q(G3)＞n−1 andn≥6,we have

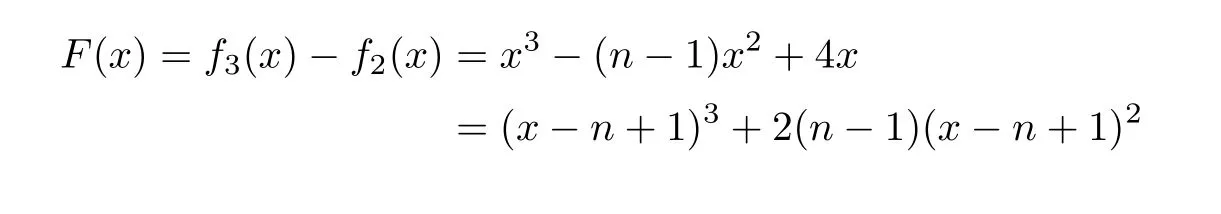
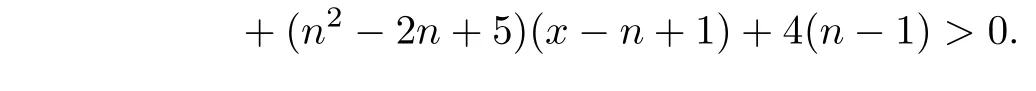
So,f2(q(G3))＜0,thenq(G2)＞q(G3).

From the above all,for anyG∈UnandG/=Gi(i=1,2,3),we have

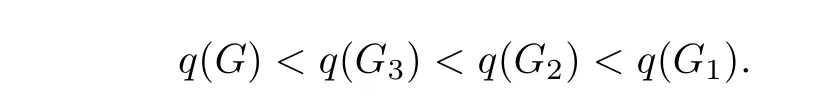
This completes the proof.

Theorem 7LetBnbe the set of all bicyclic graphs of ordernandn≥8,Gi∈Bnfori=4,5,6.Then for anyG∈BnandG/=Gi(i=4,5,6),we have

whereG4,G5andG6are shown in Fig.3.

ProofFor anyG∈Bn,from Theorem 1,ifG/=G4,thenq(G)＜q(G4).Especially,q(Gj)＜q(G4)forj=5,6.Obviously,G5andG6are all the bicyclic graphs with∆=n−2 inBn,then for anyG∈Bn,ifG/=Gi(i=4,5,6),then∆(G)≤n−3.By Lemma 3,q(Gj)＞∆(Gj)+1=n−2+1=n−1 forj=5,6.

From Lemma 2,

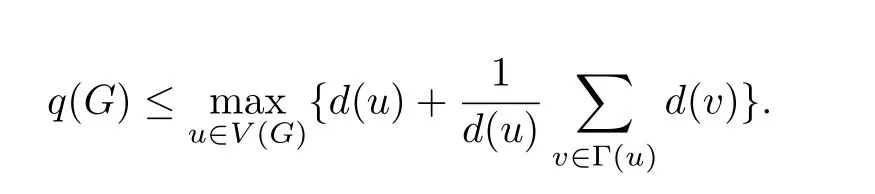
Similar to the proof of Theorem 1,we can getq(G)≤n−1＜q(Gi).

Note that

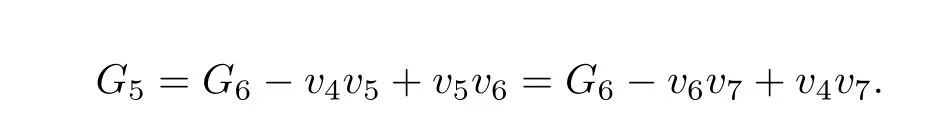
Applying Lemma 1 for the verticesv4andv6of the graphG6,we have

From the above all,for anyG∈BnandG/=Gi(i=4,5,6),we have

This completes the proof.

Remark 1Lemma 3 is also true for the Laplacian special radius of graphs.From the proof of Theorem 1,we know that Theorem 1 also holds for Laplacian spectral radius of graphs.From[3],we knowµ(G)≤q(G),the equality holds if and only ifGis a bipartite graph.And from the proofs of Theorem 2 and Theorem 3,we know that Theorem 2 and Theorem 3 also hold for Laplacian special radius of graphs.

[1]DE ABREU N M M,NIKIFOROV V.Maxima of theQ-index:graphs with bounded clique number[J].Electron J Linear Algebra,2013,26:121-130.

[2]BOLLOB´AS B.Extremal Graph Theory[M].London:Academic Press,1978.

[3]CVETKOVI´C D.Spectral theory of graphs based on the signless Laplacian[R].available at:http://www.mi.sanu.ac.rs/projects/signless-L-reportApr11,2010.

[4]CHENG Wei,TAN Shang-wang.On the maximum spectral radius of(m,n)-trees with given diameter[J].Chinese Quarterly Journal of Mathematics,2006,21(1):129-137.

[5]FENG Li-hua,YU Gui-hai.On three conjectures involving the signless Laplacian spectral radius of graphs[J].Publ Inst Math(Beograd)(N.S.),2009,85:35-38.

[6]DE FREITAS M A A,NIKIFOROV V,PATUZZI L.Maxima of theQ-index:forbidden 4-cycle and 5-cycle[J].Electron J Linear Algebra,2013,26:905-916.

[7]GUO Ji-ming.On the Laplacian spectral radius of a tree[J].Linear Algebra Appl,2003,368:379-385.

[8]GRONE R,MERRIS R.The Laplacian spectrum of graph II[J].SIAM J Discrete Math,1994,7:221-229.

[9]HE Chun-yang,GUO Shu-guang.On the signless Laplacian and Laplacian spectral radius of triangle-freek-cyclic graphs[J].Appl Math J Chinese Univ(Ser A)(in Chinese),2014,29(3):295-302.

[10]HONG Yuan,ZHANG Xiao-dong.Sharp upper and lower bounds for largest eigenvalue of the Laplacian matrices of trees[J].Discrete Math,2005,296:187-197.

[11]MERRIS R.A note on Laplacian graph eigenvalues[J].Linear Algebra Appl,1998,295:33-35.

[12]NIKIFOROV V.Some new results in extremal graph theory[J].Surveys in Combinatorics,Cambridge University Press,2011,141-181.

[13]NIKIFOROV V,YUAN Xi-ying.Maxima of theQ-index:graphs without long paths[J].Electron J Linear Algebra,2014,27:504-514.

[14]NIKIFOROV V,YUAN Xi-ying.Maxima of theQ-index:forbidden even cycles[J].Linear Algebra Appl,2015,471:636-653.

[15]TAN Shang-wang.On the Laplacian spectral radius of trees[J].Chinese Quarterly Journal of Mathematics,2010,25(4):615-625.

[16]TAN Shang-wang,GUO Ji-ming,QI Jian.On the spectral radius of trees with the given diameterd[J].Chinese Quarterly Journal of Mathematics,2004,19(1):57-62.

[17]YANG Ruo-song,WANG Li-gong.Distance integral complete multipartite graphs withs=5,6[J].Chinese Quarterly Journal of Mathematics,2016,31(2):111-117.

[18]YUAN Xi-ying.Maxima of theQ-index:forbidden odd cycles[J].Linear Algebra Appl,2014,458:207-216.

[19]YU Ai-mei,LU Mei,TIAN Feng.Ordering trees by their Laplacian spectral radii[J].Linear Algebra Appl,2005,405:45-49.