吴静

摘 要：学生在初一几何阶段如何轻松入门是初一教学的难点。读了陶行知的《“做学教合一”的总解释》后发现，教学中必须做好“接枝”工作：概念“接枝”、解题过程“接枝”、思想方法“接枝”，让学生通过动手操作、分类比较、找准关键处、提炼数学思想，将所学的几何知识“接枝”到小学知识和已有经验的基础上，让学生更快入门。

关键词：“接枝”教学；几何概念；关键处

陶行知说：“如果把别人从经验里发生出来的真知识，接取我们从经验里发生出来的真知识，那么我们的知识必定是格外扩

充。比如接树，这一种树枝，可以接到另一种树枝上去，使它格外繁荣滋长，开更美丽的花，结更好吃之果。”学生在小学时已经接触过常见的几何图形，并对它们有了一定的认识，但这种认识是具体而直观的。初中的几何问题比较抽象、理论性强，具有一定的逻辑思维能力，初一学生刚开始会有很大的不适应。因此，在几何入门阶段教师要做好“接枝”教学，使学生思维更活跃、逻辑更严密。

一、概念“接枝”

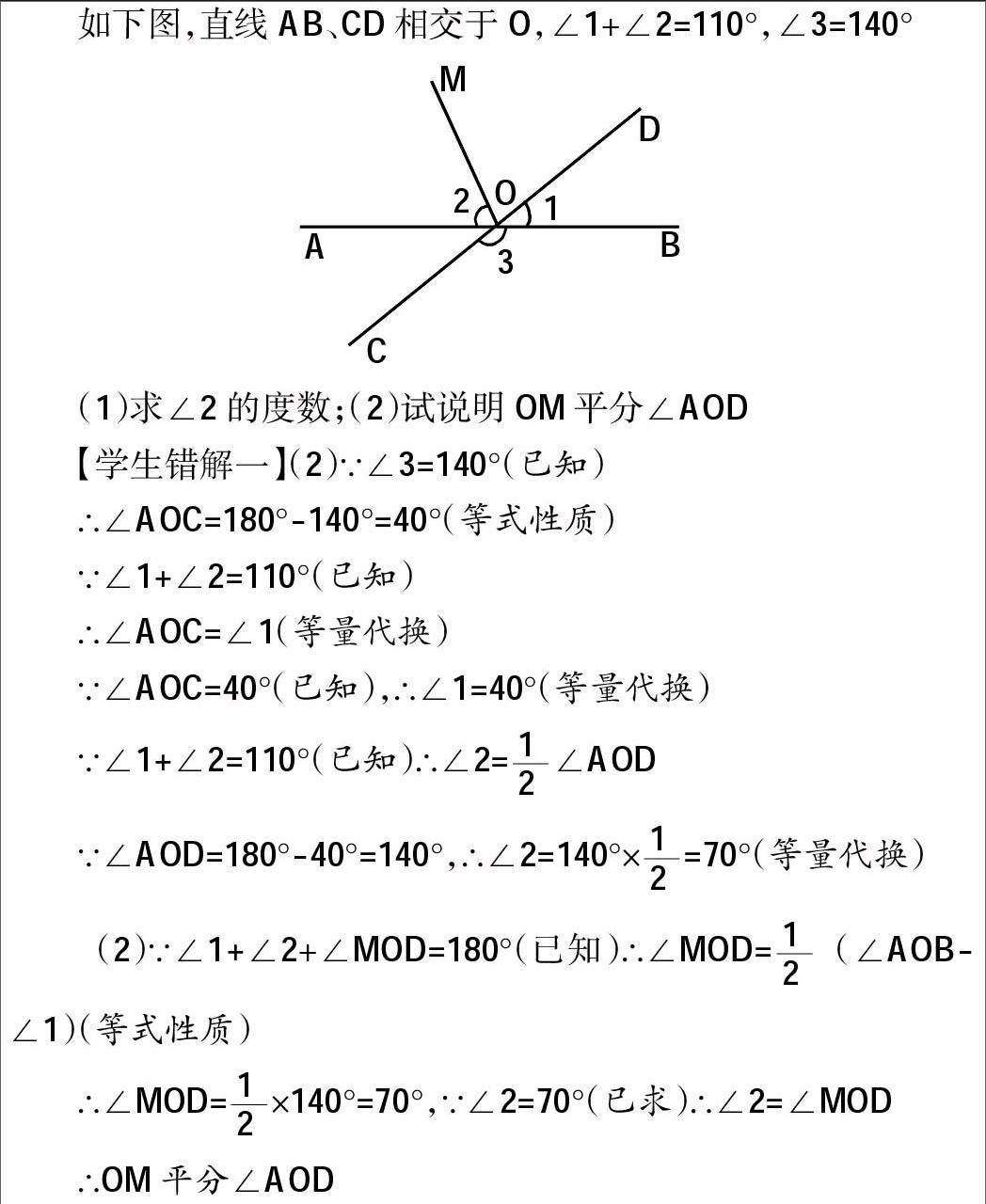
如下图，直线AB、CD相交于O，∠1+∠2=110°，∠3=140°

（1）求∠2的度数；（2）试说明OM平分∠AOD

【学生错解一】（2）∵∠3=140°（已知）

∴∠AOC=180°-140°=40°（等式性质）

∵∠1+∠2=110°（已知）

∴∠AOC=∠1（等量代换）

∵∠AOC=40°（已知），∴∠1=40°（等量代换）

∵∠1+∠2=110°（已知）∴∠2=∠AOD

∵∠AOD=180°-40°=140°，∴∠2=140°×=70°（等量代换）

（2）∵∠1+∠2+∠MOD=180°（已知）∴∠MOD=（∠AOB-∠1）（等式性质）

∴∠MOD=×140°=70°，∵∠2=70°（已求）∴∠2=∠MOD

∴OM平分∠AOD

这位学生错误解题的根源在于对角平分线的定义没有完全掌握，在解题过程中滥用角与角之间的关系。

几何概念是数学知识体系中的基本元素，是最基本的思维形式。因此，在刚接触几何概念时，教师就要做好几何概念的“接枝”工作。如在讲角平分线的定义时，笔者用如下方法加深对角平分线的理解：（1）让学生动手用多种方法画角平分线，丰富学生的感性认识。（2）对照刚学过的线段中点的定义，让学生体会两者的本质是一致的：“小的是大的，大的是小的2倍”。通过动手操作和比较说明，可以帮助学生理解概念的实质内容，体会学习新概念的意义，并让学生在具体的应用中使抽象的概念得以再现，从而巩固“新枝”的再生。

二、解题过程“接枝”

经过小学的学习，学生会通过列加、减、乘、除的式子求线段的长度、角的度数等，但不会说明理由。这种解题方法很多学生也沿用到初一的数学解题中，下面我记录了几位学生对上述几何题的解题过程。

【学生错解二】（1）∵∠3=140°∴∠DOC-∠3=∠1，180°-140°=40°

∵∠1=40°∵∠1+∠2=110°，

∴110°-∠1=∠2，110°-40°=70°

∴∠2=70°

（2）∵∠3=140°，∴∠AOC=∠AOB-∠3，

180°-140°=40°

∴∠AOC=40°

∵∠2=70°，∴∠COD-∠AOC=∠2，

∴180°-110°=70°

∵∠2=70°，∠MOD=70°，∴OM平分∠AOD

【学生错解三】（1）∵∠1+∠2=110°，∴∠1=∠AOC，∵∠3=140°，∴∠2+∠AOC=∠3

∵∠1=∠AOC，∴∠1+∠2=∠3，∴140-110°=30°，∴∠2=30°

（2）∵∠2=∠MOD（已知）∴∠2+∠MOD=180°（等量代换）

∵∠2=30°∴∠MOD=30°∴OM平分∠AOD

上述过程主要反映出学生书写不规范，思路不明确，缺乏数学逻辑性。教师要对错误率较高的题型认真分析引导。

步骤一：与小学教学“接枝”，分析解题思路。（1）求∠2?求∠1?找∠1与∠3之间的数量关系；（1）OM平分∠AOD?证∠2=∠MOD?求∠MOD的度数?找∠1、∠2与∠MOD之间的数量关系。

步骤二：板书解题过程，让学生更好地学会书写几何解题过程。

（1）∵∠AOC+∠3=180°（平角的定义）又∵∠3=140°（已知），

∴∠AOC+140°=180°（等量代换）∴∠AOC=40°（等式的性质）

∵∠1=∠AOC（对顶角相等）∴∠1=40°（等量代换）

∵∠1+∠2=110°（已知）∴40°+∠2=110°（等量代换）

∴∠2=70°（等式的性质）

（2）∵∠1+∠2+∠MOD=180°（平角的定义）又∵∠1+∠2=110°（已知）

∴110°+∠MOD=180°（等量代换）∴∠MOD=70°（等式的性质）

∵∠2=70°（已求）∴∠MOD=∠2（等量代换）

∴OM平分∠AOD（角平分线的定义）

步骤三：关键处加下划线帮助学生理清解题思路，便于学生在以后的解题过程中自己归纳、整理。就像我们要到达一个目的地，一路上的几处标志物是找准路线的关键。教师将过程中的关键处加下划线后，学生可以忽略“路上数不清的建筑物”，一目了然就能看清“标志性建筑”，从而确定顺利到达目的地的路线。

每个数学例题的教学都有明确的教学目标，有导向的作用，能让学生清楚应该朝哪条路走可以到达目的。教学不仅需要传授给学生一棵棵树木——知识点，更需要让学生把握一片片森林——知识点之间的区别和联系。教师要在例题讲解过程中让学生独立思考，根据下划线找准“标志物”，顺畅地独自走到目的地，把教师的间接经验和自己的直接经验结合起来，相互印证，达到对知识的理解和融会贯通，真正做到解题过程的“接枝”。

三、思想方法“接枝”

数学思想方法是对数学规律本质的认识，是数学的灵魂和精髓。如果教师一味地强调解题过程，那么学生对数学的掌握只能是知识的积累，机械地记忆，而不能使学生对数学知识结构和思想得到扩充和升华，技能得不到真正地发展。因此，教师在讲完例题后一定要对该题中涉及的思想方法进行概括和提升，让其“接枝”到学生的意识之中，这样才能使学生在例题中得到内化和提升。

如上述例题中涉及转化的思想方法：将∠2转化到∠1，再转化到∠AOC，当然也可以将∠2转化到求∠AOD和∠MOD。教师在总结数学思想方法时要一层一层讲，尽量讲得细致、透彻，在每个小转化处做短暂停留，确定前进方向，让学生慢慢咀嚼、消化。学生在一开始的几何学习过程中汲取有效方法，从而内化为自身的素质，学生的思维才能源源不断地得到扩展和创新。

陶行知先生说：“我们必须有从自己的经验里发出来的知识做根，然后别人相类似的经验才能接得上去。倘使自己对某事毫无经验，我们决不能了解或运用别人关于此事之经验。任何有效的教学都始于对学生已有经验的充分挖掘和利用。要求教学必须循序、系统、连贯地进行。这是经过长期教学实践反复证明的教学原则。”教育的目的不是让学生能够“复制”知识，而是使知识成为学生的主体能力，使学生能够运用知识对客观事物进行改造和创新。

初一学生的认识能力由于受到知识基础和生活经验的限制，看问题往往不全面，抓不住关键点。为此，教师在几何入门时就要让学生摒弃非本质属性，抓本质属性和关键点，在小学数学基础上得到“接枝”和提升，逐步提高学生掌握数学知识的水平和能力。

参考文献：

[1]陶行知.“做学教合一”的总解释[M].四川教育出版社，2005-06.

[2]冯恩洪.创造适合学生的教育[M].天津教育出版社，2011-07.

[3]施良方.学习论[M].人民教育出版社，1994.