孙博华

(开普半岛技术大学机械工程系，开普敦 南非7535)



量纲分析以及应用

孙博华

(开普半岛技术大学机械工程系，开普敦 南非7535)

本文系统介绍了量纲分析方法和如何使用量纲分析的六步法，通过几个典型应用(点源爆炸、管流阻力和黏性流体中小球运动)展示了量纲分析的普适性.

量纲;π定律;相似性

0 引言

随着人类对自然界探索活动的深入，遇到的问题也愈来愈复杂，往往涉及多尺度、多层次、多材料和多物理的耦合问题.虽然有各种各样的分析方法，但都有其局限性，我们现在的问题是，是否有一种普遍方法来处理这些复杂的问题呢？回答是肯定的，这个普遍适用的方法就是量纲分析方法，它是探讨科学规律、解决科学和工程问题的一个普适方法，是一门非常值得学习和掌握的科学工具.

解决一个复杂问题，除了需要理解具体问题的物理理论外，还需要掌握与物理概念密切相关的量纲分析方法和相似论.它们既可以用于数据整理，也可以在不求解问题前就对问题有个定量和定性的把握.对于有些复杂问题，建立其数学模型有时可能非常困难，或者方程非常复杂难以求解，或者求解的过程非常复杂不便于实际应用.有时需要做试验，而实际尺寸很难在试验条件中实现，必须缩小尺寸做模型试验，这时必须要求满足一定的相似条件，这种条件必须建立在量纲分析和相似论的基础上才能建立.一般来讲，对于复杂问题，特别是研究开始时一般都要先进行量纲分析和相似性分析，尽量找出一些一般性规律，发现主导参量，细化演化过程，以便在建模和分析时简化问题.

量纲分析(dimensional analysis)很难说从何时开始，基本上它是推广古希腊几何中的相似与比例的观念.很多科学大师如Newton、Fourier[1]、Maxwell[2]等处理问题时内心深处其实是有量纲的概念, 但不成系统.法国数学家J.Fourier的名著Analytical Theory of Heat(热的解析理论)就有量纲分析的论述，20世纪初量纲分析才逐渐成形，并且是物理学、数学中建立数学模型的重要方法之一.牛顿第二定律F=ma的物理关系，其方程式应该与计量物理量的单位无关.这导致一个重要结论：任何有意义的定律，对于其方程式的每一个计量单位，都必需是齐次方程式.这个认识的最终形式成为π定理，即假设一个有物理意义的方程式具有n个变数与m个基本量纲，π定理描述怎样将这方程式等价地写成具有n-m个无量纲参数的方程式.更重要的是，从给定的变数，这定理给出了一种能够计算这些无量纲参数的方法.

通过量纲分析可以检查反映物理规律的方程在计量方面是否合理，即利用物理定律的量纲平衡(齐次原理)确定各物理量之间的关系.一个成熟的物理学家如果要探究某一个问题，往往是从定性到半定量至定量的分析过程，从量纲分析入手.

1 从一个故事开始——点源强爆炸

在量纲分析发展历史上一个特别有名的案例，是第二次世界大战期间英国力学大师G.I.Taylor的点源强爆炸研究，他发现了冲击波球面半径与时间的2/5成正比的规律，并从照片预测了世界第一颗原子弹的当量，曾引起很大的国际社会反响，害得美国要调查是否有泄密事件.这个问题的解决展示了量纲分析解决复杂问题的强大能力.

在二战的困难时期，1940年英国著名科学家GeorgeThomson邀请G.I.Taylor参加一个工作午餐，Thomson是刚成立的英国铀军事应用委员会的主席，他告诉Taylor英国要制造一种利用核反应产生巨大能量的炸弹，不过那时还没有使用原子弹这个名词.

传统炸弹的机械效能，是通过在有限的空间里短时释放大量高温高压气体获得的.而对于这种新型炸弹，当时的问题是希望了解这种在极端聚焦的没有伴随气体的点源强爆炸的机械效能是否与传统的炸弹类似[3-5].

就在他们这次讨论这个问题之前，英国收到美国著名爆炸专家G.Kistiakovsky*G.K.出生于乌克兰基辅，哈佛大学教授，曾领导研制第一颗原子弹内爆点火的爆炸镜头explosive lens.的报告，他认为即便这种炸弹能爆炸，其威力也没有期望的那么大.到底情况如何需要尽快研究.R.W.Clark

在《TheBirthoftheBomb》一书中指出，当时他们认为全英国只有一个人可以解决这个问题，这个人就是剑桥大学的G.I.Taylor教授.

对于这个科学问题，Taylor思考和计算空气在瞬间爆炸产生的运动和压力.他认为爆炸会产生一个热冲击波，即一个点源强爆炸瞬间释放巨大但有限的能量E，将对其周围的空气进行急剧的压缩和加温，并以超过声速的球形冲击波向外急速膨胀.

图1 原子弹爆炸的球形冲击波

他列出了问题的流体力学偏微分方程组，发现这个方程组是非线性的，当时无法求解，怎么办？这时Taylor想到借助量纲分析这个有力工具来研究这个问题.

设空气绝热系数γ(表征空气的可压缩性，无量纲)，在爆炸时间t时球形冲击波的波阵面半径是R，波阵面相当于一个球形边界面，内部是超热的火球，外面是正常大气，其密度为ρ0，压强比球内压强小几个数量级可以忽略不计.这样，这个复杂的问题就简化成一个只有5个参量的问题，即希望知道球形冲击波的波阵面的半径

(1)

这里的符号f只代表是一种函数关系，不是具体的一个函数.下面使用量纲分析来研究一下这些量之间的关系.

这里有n=5个参量见表1，基本量纲有质量m，长度L和时间t,即j=3.

表1 点源强爆炸参量的量纲

根据π定理，可以构造出k=n-3=2个无量纲的Π.取E,t,ρ0为重复变量，有关系

由于γ是无量纲量，所以α=β=λ=0，即Π2=γ.

对于Π1，有

(4)

可得到幂次数为

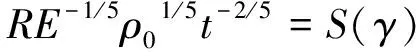
(5)

这样就得到Π1

(6)

根据量纲分析理论，就有关系Π1=S(Π2)，即

(7)

其中S(γ)是常数，所以就得到球形冲击波的波阵面的半径

(8)

以上就是Taylor的时间2/5幂次律，冲击波的波阵面半径是时间的2/5幂次方，后来计算确定S(γ)≈1.033.

从上式可得球形冲击波的波阵面上的速度

(9)

可见球形冲击波的波阵面上的速度是变化的，并且随时间的增大而衰减，当时间很大时速度趋于零.

球形冲击波的波阵面上的加速度

(10)

球形冲击波的波阵面上的加速度是变化的，是加速度冲击波，而且也随时间增大而衰减.

球形冲击波的波阵面后面的压强

(11)

球形冲击波的波阵面上的压强，在爆炸中心附近非常大，并随时间迅速衰减.

到这里量纲分析的介绍本来可以结束，但与此有关的故事在科学技术史上也有一定的意义，在此顺便介绍.故事是这样的，1941年6月27日Taylor给英国有关机构提交了报告.当时参加美国原子弹Manhattan工程的大科学家John von Neumann也研究同一个问题，在提交报告前他在周末检查报告中的168个公式，于1941年6月30日(星期一)提交给Los Alamos实验室[6]，比Taylor晚了3天！

由于保密的原因，当时以上两个报告都没有公布.Taylor在1950年才允许发表其研究成果，John von Neumann的结果在1947年发表在Los Alamos的Blast Wave报告第二章中[7].

同一个问题，苏联参加原子弹研究的L.I.Sedov也进行过独立研究，结果没有保密而是于1946年发表在公开的学报上[8].

图2 世界第一颗原子弹Trinity从0.1ms至 1.93ms爆炸火球的照片

在Taylor(1950)的第二篇论文中[5]，他利用1947年美国公开发表的原子弹爆炸火球照片(见图2)，从中测量出时间和半径，用公式E=[S(γ)]-5ρ0R5t-2计算预测了美国第一颗原子弹的爆炸当量是

(12)

据文献上介绍，预测结果发布后很让美国政府难堪，虽然爆炸照片已经公开了，但这个爆炸当量当时是高度绝密的参数.提取照片的数据利用量纲分析公式预测原子弹的当量是Taylor的一大贡献，得到了超出科学界的巨大社会效果，所以Taylor的结果特别有名.

怎么连公式都不用，Taylor就解决了这个问题？太神奇了！那么，量纲分析到底包括哪些内容，如何使用它来解决科学和工程中的问题？下面就系统介绍量纲分析的理论.

2 量纲分析的基本概念和π定理

量纲分析有它的核心概念和定理，理解它们对于灵活使用量纲分析来解决问题非常重要.量纲分析核心知识点包括量纲概念、7个基本量纲单位、量纲幂次定理、量纲一致性定律、π定理、量纲分析6步法、模型实验与原问题的相似模数都必须相等等概念.

2.1 量纲和基本单位

任何物理量都有量纲或单位，该物理量的大小就是这个单位的多少倍，即一个标量乘这个单位.如长度10米， 其中米是度量这个长度的单位，而10是这个长度和米所表示的单位长度的比例.很明显，用来度量这个物理量的单位和这个物理量本身一定是同一类型的量，或者说，这些量的量纲是相同的.长度的量纲我们用L来表示，而不特别说明具体是用长度的米、厘米还是毫米，只要是长度量纲就行.

当然也有一些量是没有量纲，我们就称其为“无量纲”量，如角度和一些导出的量.

物理世界千变万化，看起来非常复杂，但可以庆幸的是，基本的物理量量纲单位一共只要7个(见表2)，所以我们有结论：基本的物理量量纲单位一共只要7个；所有其他的物理量都是其组合的导出单位.

表2 基本物理量量纲和符号

从一个问题涉及基本物理单位的个数多少基本可以预测这个问题的复杂程度，当然越多越复杂，但最多就是7个基本的物理单位.近几年来，科学界比较关注的多物理问题从本质上看就是这些问题涉及多个基本物理量.

比如，纯力学类系统，只会涉及3个基本量(质量，长度和时间)，如果考虑温度变化的热力学过程就需要加上基本量温度.

2.2 量纲的幂次定律

量纲是物理量的种类属性，物理量的量纲反映该物理量随基本量的单位变化而变化的倍数.物理量的量纲如何来表达，它一般是什么形式？在力学系统中，基本量纲有3个，长度L，质量M和时间T，这个系统中的任何的物理量Y都可以表示成Y=LaMbTc, 其中a,b,c为实数.

一个无量纲的纯数A也可以这样表达，只是其幂次都为零，即A=L0M0T0.其实这个结果是一般性的.一个问题的基本量纲一旦确定，其中的任何物理量都可以表达成基本量纲的幂次形式，

物理量纲的幂次定律: 任何物理量的量纲公式都是基本量纲的幂次单项式的形式.

2.3 量纲一致性定律

苹果(物理量)加雪梨(物理量)等于什么？量纲不同的物理量是不能相加的(见图3).

量纲一致性定律: 每个在公式中相加的量其量纲必须一致.

图3 不同性质的物理量不能相加

例如，Einstein公式，E=mc2， 量纲关系是ML2T-2=M(L/T)2.如果在推导公式时发现某些项的量纲之间不同，那么一定是推导有误，必须修改以保证公式中的每一项的量纲都一致.

与量纲一致性原理相关的一个原理是说描写真实世界的物理定律中的物理量与测量这些物理量的单位无关.比如力学的Newton定律F=ma中的质量可以使用kg，也可以使用g，不管用什么单位，公式都应该成立.这种与物理量单位无关反映了物理定律一个非常重要的不变性原理.

2.4 π定理

1914年Buckingham[9,10]发表一篇有关量纲分析的重要定理，由于在论文中使用希腊字母π表示无量纲量, 1922年被美国学者P.W.Bridgman在其专著《Dimensional Analysis》[11]中命名为Buckinghamπ定理.Bridgman的这部书是他在哈佛大学给研究生的5次讲座基础上整理而成，是世界上第一部量纲分析专著.由于量纲分析理论之后没有什么变化，从现代的角度看这部书完全一点都不过时，多次再版发行，不愧为是一部名著.1946年，Bridgman由于高压物理的研究获得诺贝尔物理学奖.有关π定理，据说俄罗斯学者于1911年曾独立发现[12].

π定理: 设有一个物理关系，f(x1,x2,x3,…,xn)=0，由一组量纲不同的物理量x1,x2,x3,…,xn所组成.设在这组物理量中有j个量纲是相互独立的，并且选作为基本单位量纲，这个物理关系一定可以用k=n-j个无量纲量Π1,Π2,…,Πk完全表示出来，即

(13)

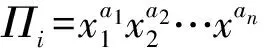
这里的j不能是任意多，基本量纲单位只要7个，所以j的最大值是7，一般情况下j≤7.但在定向量纲分析中，可以通过引入长度的方向性，增加基本量纲，但本质上也没有增加物理基本单位，仍然是7个.从以上的π定理的表述看，可能给人的感觉是量纲分析很困难.其实只要对问题有比较好的物理了解，使用下面的6步法，就可以较快地得到问题的标度律或相似关系.

2.5 量纲分析的6步法

π定理给出了构造无量纲量Π的一般方法，在此基础上人们总结出一个简单的6步方法[13]列于表3.

表3 量纲分析的6步法

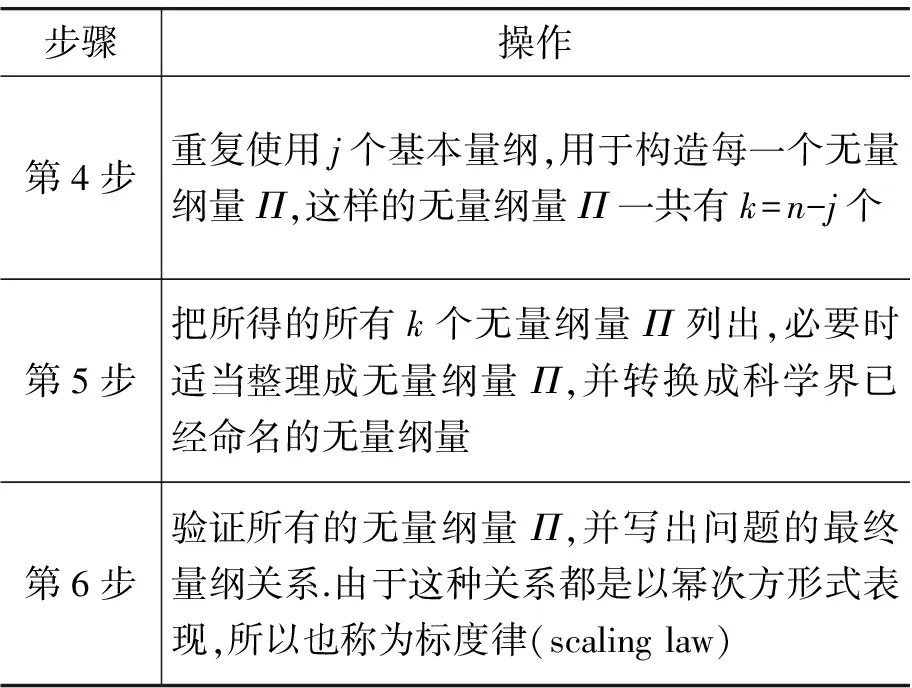
续表

应当指出，在第3步中有“猜测j值”，这就给人一种不确定的感觉，从而使量纲分析有些随意性，由于这个原因，量纲分析也的确有些技巧或“艺术”成分.一个复杂问题通过量纲分析解决后往往会给人一种智慧的冲击和享受，所以好的量纲分析结果一般都是科学大作.

2.6 量纲分析的难点

虽然π定理给出了构造无量纲量Π的一般方法，但人们在使用中会感到一定的困难[14].

(1) 如何确定问题的物理量，就是参量n的问题.在一个物理问题中究竟哪些是必要的物理量，有时很难决定，特别是新的科学问题，问题本身可能还没有确定.多余地加进一些关系不大的物理量，常常给我们增加很多分析的复杂性，但过少的物理量显然不能解决问题.这里就需要有高深的科学修养，具体问题具体分析，这个地方就有“技巧”和“艺术”的成分.量纲分析需要非常丰富的物理知识和对问题的深刻理解.

(2) 如何决定作为基本量纲的物理量，就是j值的问题.在n个参量中，选j个量作为基本量，这时到底选哪个量作为基本量，就是一个很关键的问题，显然不同的选择，会构造出不同的一组无量纲量Π.这个重要的问题可惜没有一个标准和规律可循，从而不同人会得到不同的结果.这就有结果好坏的问题，是量纲分析中难度系数最大的问题.

(3) 无量纲量Π不是唯一的，其相互的乘除和幂次都是无量纲量！这时需要把导出的无量纲量与历史上科学界已经命名的参量比较，并改写成该量的传统表示.

以上是量纲分析学习和使用时的难点，必须通过实践训练才能掌握好这个工具.学术上讲，其中的一些问题只有通过相似论来解决.但是，应用相似论，就要求使用物理问题的基本方程.在很多实际问题中，问题的基本方程常常还不很明白.在这些没有基本方程的复杂问题中，量纲分析就比较有用.所以，如果你研究的问题非常复杂，还没有搞得太明白，最好不要贸然开始，建议先用量纲分析试试问题的深浅.

确定重复变量是量纲分析的难点，一般情况要从物理上思考才会比较准确.比如管道中流体流动摩擦阻力的问题，其中有管道、液体和流动3个因素，它们的相互作用导致摩擦阻力，重复变量就必须包括管道和流动液体两个方面，所以可以取管道的直径D、液体的密度ρ和流动速度v作为重复变量.

3 管内液体流动的摩擦阻力

设一个圆管(见图4)的直径为D， 不完全光滑有粗糙度ε(长度量纲)，流体的密度是ρ，流动速度v，动力粘度μ，摩擦切应力τw(是摩擦阻力的来源)，问题是需要确定τw与其他量的关系.

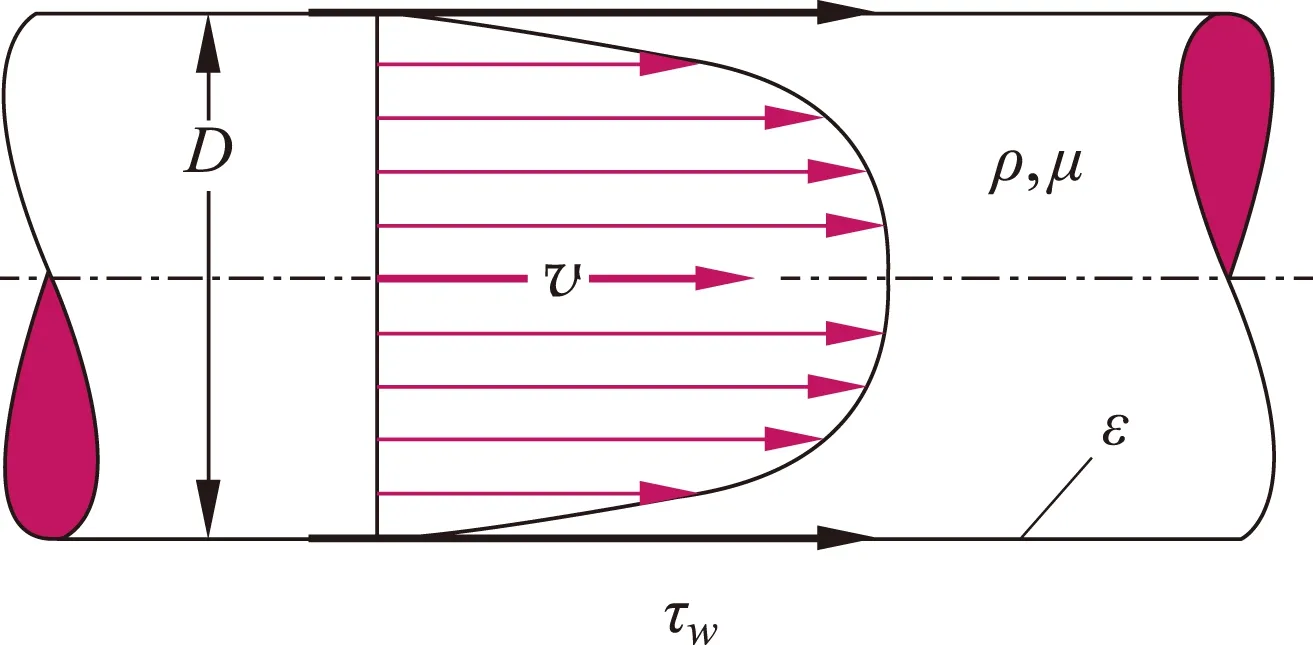
图4 管流的摩擦阻力

第1步： 列出问题所有的参量(有量纲的变量，无量纲变量和常数)并计算其个数，设一共有n个参量.

对于这个问题，我们有6个参量，即n=6.这个问题的目的就是要确定关系

(14)

第2步： 列出所有n个参量的量纲(见表4).

表4 管流参量的量纲

第3步： 这个问题的基本量纲有L,M,T共3 个.作为第一次猜测，取j值等于问题中基本量纲的个数，即j=3.这样我们就有k=n-j=6-3=3，这样就会有k=3个无量纲量Π.

第4步：j值是3，我们要从6个参量中选择3 个作为问题的重复变量，无量纲的攻角不选，因变量τw不选，动力粘度μ已经包含了所有的基本量纲L,M,T，我们取D,v,ρ作为重复变量.

第5步： 把所有的k个无量纲量Π列出，必要时适当整理无量纲量Π转化成科学界已经命名的无量纲量.

我们把τw与重复变量做一个乘积，重复变量的幂次为待定.

(15)

把表中的参量基本量纲代入到上式，并注意Π是无量纲量，得到合并同类项，两边同一量的幂次必须相等，得到待定常数a=-2,b=0,c=-1.

把确定的a和b代入到Π，得到这个问题Π

(16)

其中的Π1改写成传统的Darcy摩擦阻力因子fD

(17)

类似，我们用空气粘度μ代替τw， 重复计算就可以得到Π2

(18)

可以得到另一组a=-1,b=-1,c=-1，所以

(19)

这个Π2就是Reynolds常数Re的倒数，可以修改成传统表示

(20)

同样可以得到第3个Π3， 就是粗糙度δ与管直径的比值，传统称为粗糙度系数

(21)

第6步： 验证所有的无量纲量Π，并写出问题的最终量纲关系.

(22)

得到摩擦阻力系数为

(23)

对于这个问题，我们没有建立问题的方程更没有求解，得到了摩擦阻力因子与粗糙度系数的关系公式，很神奇！当然，量纲分析不能完全确定一切，待定常数F(Re,ε/D)，它必须通过其他方法(如试验)确定.

对于粗糙度系数ε/D为零的管流，在层流情况下fD=64/Re;对于湍流是不同的结果fD=0.316Re-1/4.

对于速度v很大的极限情况，可认为Re→∞，对于这个问题F(Re,ε/D)就只是粗糙度系数ε/D函数.

如果管道完全光滑即粗糙度系数为零，即

(24)

这时摩擦阻力因子fD是常数！即有切应力τw=Cρv2，其中C是常数.

4 定向量纲分析

以上介绍的通常量纲分析除了本文2.6节的难点外，还有些先天不足，比如说长度和速度的方向无法表示，这就使运用量纲分析处理一些固体力学问题时有一定的限制，在固体力学中量纲分析不很成功，量纲分析需要改进，需要引进定向量纲的概念[14-17].量纲分析的一些不合理的地方是：

(1) 角度由于是无量纲量，它只能隐含在待定函数中，它本身无法进行量纲分析，比如研究机翼升力的攻角α，只能隐含地表现在函数f(α)中，但无法从中提取出来.

(2) 所有的应变都是无量纲量，与角度类似其本身无法进行量纲分析，只能隐含在待定函数中，弹性应变与塑性应变量纲也一样，无法区分开来.而固体力学中应变无处不在，这可能是通常量纲分析在固体力学中应用不理想的一个原因.

(3) 有些物理量本身之间没有什么联系，但其量纲却相同，在量纲分析中无法把它们分开.例如物质质量和惯性质量的量纲都是M，无法区分它们；频率，应变率，角速度的量纲都是T-1；所有Young弹性模量、剪切模量、应力的量纲都是LMT-2；角动量的变化率、能量和梁板壳弯矩的量纲都是L2MT-2.

(4) 基本单位最多只有j=7个，力学系统的基本单位才有j=3个(长度，质量和时间)，对于力学系统来讲，如果问题有n=4个参量，就可以得到一个Π，这种情况是最好的，因为只有一个Π，它就只能是一个常数，所有的量就不再隐含在函数里了，比如肥皂泡的例子中Π就是一个常数.

这里就出现一个问题，是不是可以在量纲分析的框架下，通过合理增加一些基本量纲，从而减少问题的Π个数，达到简化问题的目的？

Huntley提出定向量纲(Directed Dimension)概念[15]，Siano提出(orientational analysis)取向分析[16,17].

具体讲，Huntley的定向量纲基本思想有两点：

(1) 考虑矢量的大小和方向，原来只考虑大小.如沿x方向上的长度记成Lx，x坐标方向的速度记成vx=Lx/t，

(2) 区分物质质量(mi)和惯性质量(ms)的量纲.

Siano的取向分析，特别引进方向符号lx、ly、lz代表3个方向，没有方向的标量使用符号l0.这样Huntley的Lx就可以表达成Lx=Llx.也可以表示角度和三角函数等.

4.1 炮弹的水平距离

问题： 炮弹在高度为H处用初始速度v平射，求抛到地面的水平距离R.炮弹在以v抛出后，在地球引力(重力)的作用下靠惯性飞行，这个问题的参量有H,v,R和重力加速度g，即有n=4个参量(见表5).

表5 炮弹平射参量的量纲

从中可以看出，这个问题的基本量纲是长度L和时间t，即j=2，所以本问题有k=n-j=2个无量纲Π:

(25)

(26)

所以有关系

R/H=f(gH/v2)

(27)

这就是使用通常量纲分析获得的结果.关系式(27)只能告诉我们水平距离R与初始高度H成正比，无法给出与初始速度的明确关系信息，我们不满足这个结果，希望获得更多的信息.

让我们区分速度的方向，以及水平距离和高度方向.问题的参量有H、v、R和重力加速度g，即有n=4个参量(见表6).

表6 炮弹平射扩充参量的量纲

同一个问题，仍然有4个参量，但基本量纲多了，现在是3个(Lx,Ly,t),这时就只有一个无量纲Π:

(28)

由于式(28)只有一个Π，所以这个Π必须是常数C，问题的解答是

(29)

讨论： 式(29)只有一个待定常数，物理关系非常简单，R与H的关系是抛物线关系，理论推导知道其中的常数C=2.

5 量纲分析的不完全相似问题

还有一些问题，其中有的Π非常大而同时有些Π又非常小，出现所谓的奇性问题.比如在以上的例子中曾看到雷诺数Re很大的情况.这需要引进量纲分析的不完全相似概念.

以上讨论的量纲分析属于完全相似的情况，如果其中的无量纲Π趋于无限大或零，这时的量纲分析属于非完整相似情况，这种情况的相似性一般将被破坏.为了也可以近似处理这类问题的相似性，G.Bareblatt在1979年提出一种处理这类相似性的渐进方法[18].

其基本思想是，比如，不失一般性这里只举有3个Π的情况.如一个问题按正常操作得到无量纲关系

(30)

假如在Π2→0的情况下Π1的极限存在，现在的问题是Π1可以是什么形式？类似使用函数的Taylor级数展开，Barenblatt建议式(30)改成如下形式

(31)

其中式(31)的幂次α是待定常数.

如果Π3→∞的极限也存在，式(31)可以改写成

(32)

显然，如果极限f(∞)存在，α必须是一个常数，在最简单的情况可以取幂指数α=1.

6 小球在黏性液体中运动的速度

假如有一个小球(Reynolds数非常小)在黏性液体中自由下落或上升(见图5)，它的速度起初被加速，但是，由于液体的黏性阻力随速度的增加而增加，小球的速度越来越低最后达到一个速度v，现在的问题是如何确定这个速度？这个问题如果利用流体力学的方程来精确求解，其实是非常困难的，这里使用量纲分析来分析这个问题.

图5 小球在黏性液体中运动

从物理直觉上，小球运动受到浮力和液体阻力的联合作用，显然这个速度问题与以下几个物理量有关系，具体是什么关系目前不知道.这些相关物理量是，小球的特征尺度为R(小球不一定必须是圆球！如果是圆球，特征尺度R就是圆球的半径)，ρs、ρf分别是小球和液体介质的密度，μ是液体的动力黏性系数，由于是自由落体显然与重力加速度g有关. 这些参量的量纲列于表7.

表7 小球在黏性液体中运动问题的各参量的量纲

这个问题可以表示成

(33)

从物理上看，下落的速度应当与小球和液体的密度差Δρ=ρs-ρf成比例，这样上式可以改写成

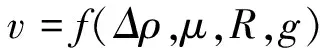
(34)

不使用以上方法，直接设速度v可以表达成以下幂指数的形式

v=CRa(ρs-ρf)bμcgd

(35)

其中C是一个常数.把这些参量的量纲代入这个关系，根据量纲一致性原理，得到用a表示的其他幂指数b=(2a-1)/3,c=(1-2a)/3,d=(1+a)/3，所以有关系

(36)

现在的问题是如何确定其中的a?再从物理上考虑，引起小球运动的单位体积浮力是(ρs-ρf)g，所以上式中的(ρs-ρf)必须与g具有相同的幂指数，即

(37)

可以得到a=2.至此，就得到了小球下落或上升的速度

(38)

对于圆球情况，理论上可以确定C=2/9，这就是著名的Stokes公式.不过与理论推导相比，这里推导的简单程度简直难以置信.从这个表达式可以看出，小球下落或上升的速度与小球的面积即R2尺度成正比，与密度差Δρ成正比，特别是小球密度大于液体时小球下落，反过来，小球上升.

物理上，在这个速度，小球运动处于浮力Fg与液体阻力Fd相互平衡即相等的状态Fd=Fg(见图5).

对于小球是完全的球形，这时其浮力Fg根据阿基米德定律得到

(39)

利用式(38)，浮力的表达式可以改写成速度的函数如下

(40)

所以，可以得到小球在黏性液体中运动的阻力为

Fd=6πμRv

(41)

这就是著名的Stokes阻力公式，它是由G.G.Stokes于1851年推导出来.不要看这个公式简单，但它对许多研究至关重要，据Dusenbery介绍，这个公式已至少产生3项诺贝尔奖[19].

可能你已经注意到，如果我们使用6步法，对于v,Δρ,μ,R,g这5个参量，我们可以得到2个无量纲的Π，即

(42)

根据π定律，我们可以得到关系Π1=f(Π2)，也可以写成1/Π1=f(1/Π2)，即

(43)

(44)

这里的关系也可以从物理上进一步理解，浮力Fg是正比于尺度R3，Fd阻力是正比于尺度R，所以小球运动速度正比于尺度R2.

7 结语

本文系统介绍了量纲分析方法的基本概念和理论，通过实例展示了量纲分析的强大功能和获得结果的普适性.从以上的几个例子可以看到，不用公式就可以得到有关的结果，这往往也会给人产生一个错误的感觉，就是量纲分析和应用好像非常容易，但实际应用的时候又觉得无从下手，好像是一门“艺术”.

为了可以更好地使用量纲分析方法，特别提醒读者注意以下几点：

(1) 不用公式但需要对问题有深刻的理解：使用量纲分析方法的核心是取决于你对于所研究问题的物理过程的理解深度，理解越深参量选择越准确，越能得到有价值的结果；

(2) 需要与其他方法结合：量纲分析只能给出问题的普适结果，不能完全确定其中的全部关系，需要结合其他方法(实验、理论分析或数值计算)进一步确定其中的系数；

(3) 对结果要进行物理分析：对于量纲分析得出的结果，一定要从物理上进行分析，以期可以进一步简化.

应当指出，量纲分析方法可以应用到各种各样的科学问题，有关在其他方面的应用，请参考文献[20-23].

致谢： 感谢清华大学教授陈难先院士把我推荐给《物理与工程》，感谢王青主编的约稿邀请，以及编辑部主任钱飒飒对我准备论文时的协助.

[1] Fourier J B J. Analytical theory of heat[M]. New York: Dover Publications, 1955.

[2] Maxwell J C. A treatise on electricity and magnetism[M]. Cambridge: Clarendon Press,1891; New York: Dover Publications, 1954.

[3] Taylor G I. The formation of a blast wave by a very intense explosion[R]. Civil Defense Research Committee, Report RC-210, 27 June 1941.

[4] Taylor G I. The formation of a blast wave by a very intense explosion-Part 1[C]//Theoretical discussion, Proceedings of the Royal Society of London. Series A, 1950, 201(1065): 159-174.

[5] Taylor G I. The formation of a blast wave by a very intense explosion-Part 2[C]//The atomic explosion of 1945. Proceedings of the Royal Society. Series A 1950, 201(1065): 493-509.

[6] von Neumann J. The point source solution[R]. NDRC. Div. B. Rept. AM-9, June 30, 1941.

[7] von Neumann J. Blast wave[R]. Los Alamos Sci. Lab. Tech. Series, Vol.7, Part 2, H. Bethe,ed., August 13, 1947, LA-2000.

[8] Sedov L I. Propagation of strong blast waves. Prikladnaya Matematika i Mekhanika[J]. Appl. Math. Mech., Leningrad). 1946,10: 241-250.

[9] Buckingham E. On physically similar systems: Illustration of the use of dimensional equations[J]. Phys. Rev. 1914, 4: 345-376.

[10] Buckingham E. The principle of similitude[J]. Nature. 1915,96: 396-397.

[11] Bridgman P W. Dimensional analysis[M]. New Haven:Yale University Press, 1922.

[12] Riabouchinsky P. On principle of similitude-letter to the editor[J]. Nature, 1915, 95: 591.

[13] Çengel Y A, Cimbala J M. Fluid mechanics fundamentals and applications[M]. New York: The McGraw-Hill Education, 2010.

[14] 钱伟长.应用数学[M].合肥：安徽科学技术出版社，1993.

[15] Huntley H E. Dimensional analysis[M]. New York: Dover, 1967.[16] Siano D. Orientational analysis—A supplement to dimensional analysis-Part 1[J]. J. Franklin Institute. 1985, 320(320): 267.

[17] Siano D. Orientational analysis—Tensor analysis and the

group properties of the SI supplementary units—Part 2[J]. J. Franklin Institute. 1985, 320(320): 285.

[18] Barenblatt, G I. Similarity, self-similarity and intermediate asymptotics[M]. New York:Consultants Bureau, Plenum Press, 1979.

[19] Dusenbery D.B. Living at micro scale[M]. Cambridge: Harvard University Press. 2009:49.

[20] Sedov L I. Similarity and dimensional analysis in mechanics[M]. New York: Academic Press, 1959.

[21] 谈庆明.量纲分析[M].合肥：中国科技大学出版社,2007. [22] Sun B, The temporal scaling laws of compressible turbulence[J]. Mod. Phys. Lett. B, 30, 1650297(2016)[14 pages]DOI: http://dx.doi.org/10.1142/S0217984916502973.

[23] 孙博华.量纲分析与Lie群[M].北京：高等教育出版社，2016.

[24] 中华人民共和国国家标准.有关量、单位和符号的一般原则[M].北京：中国标准出版社，1993.

■

DIMENSIONAL ANALYSIS AND APPLICATIONS

Sun Bohua

(Department of Mechanical Engineering, Cape Peninsula University of Technology, Bellville 7535, Cape Town, South Africa)

The paper gives a systematical introduction on dimensional analysis(DA), and proposes a six-steps on how to use the dimensional analysis, the universality of the DA will be shown by some typical examples, such as, point blast, pipe flow and a small sphere moving through a viscous fluid.

dimension;πtheorem; similarity

2016-09-15

孙博华. 量纲分析以及应用[J]. 物理与工程，2016，26(6)：11-20.

孙博华，1963年出生于徐州铜山，现任南非开普半岛技术大学教授，南非科学院院士. 1983年获长安大学(前西安公路学院)工程力学学士学位，1986年获西安建筑科技大学(前西安冶金建筑学院)结构力学硕士学位，1989年获兰州大学力学理学博士学位，曾于1989-1993年在清华大学、荷兰Delft(代尔夫特)大学、德国Ruhr(鲁尔)大学(洪堡AvH学者)和南非开普敦大学做博士后研究工作.1986年在西安冶金建筑学院任助教，1995年至今在南非开普半岛科技大学工作并曾担任研究员、讲师、教授、Senate(校务委员)，2002年12月至2008年1月协助暨南大学校长刘人怀院士创办中国第一家全英授课国际学院并担任首任院长.孙博华教授长期从事力学和力学技术及其应用数学方面的研究，在壳体理论、智能结构、MEMS光导和波导陀螺、湍流和非协调变形场等方面做出过系统研究，曾编写《Toroidal Shells(英文)》和《量纲分析与Lie群》等6部专著，目前的主要研究兴趣是连续介质力学、张量与微分形，并关注量子引力问题. 2010年入选年度海外华人十大新闻人物. 2016年9月起担任西安建筑科技大学第三届校董会副主席.E-mail:sunb@cput.ac.za