Chanh KIEU

Department of Geological Sciences，Indiana University，Bloomington，Indiana 47405，USA

The Dynamics of Barotropic Vortex Merging

Chanh KIEU*

Department of Geological Sciences，Indiana University，Bloomington，Indiana 47405，USA

The merging of multiple vortices is a fundamental process of the dynamics of Earth’s atmosphere and oceans.In this study，the interaction of like-signed vortices is analytically and numerically examined in a framework of two-dimensional inviscid barotropic flows.It is shown that barotropic vortex interaction turns out to be more intricate than simple merging scenarios often assumed in previous studies.Some particular configurations exist in which the vortex merging process is never complete despite strong interaction of like-signed vortices，regardless of the strengths or distances between the vortices. While the conditions for a complete vortex merging process introduced in this study appear to be too strict for most practical applications，this study suggests that careful criteria for vortex mergers should be properly defined when simulating the interaction of vortices，because the merging may not always result in a final enhanced circulation at the end of the interaction，as usually assumed in the literature.

barotropic vortex，vortex merger，vortex dynamics，binary vortex interaction

1.Introduction

The vortex merging process by which multiple vortices of the same sign interact and are eventually aggregated into a broader circulation at the end of their interaction plays an important role in studies of atmospheric and oceanic circulations.Various fluid processes have been shown to be characterized by well-defined and coherent vortex interactions ranging from minute fluid vortex eddies to large-scale circulations（e.g.，Yasuda，1995；Ferreira and Schubert，1997；Lansky et al.，1997；Cerretelli and Williamson，2003；Josser and Rossi，2007；Rodr´ıguez-Marroyo et al.，2011；Yamazaki and Itoh，2013；Luo et al.，2014；Tallapragada and Kieu，2014）. For specific mesoscale circulations in the atmosphere，vortex mergers are often connected to swift changes in development of tropical disturbances，which have significant impacts on the formation and subsequent track and intensity changes of tropical cyclones（Lander and Holland，1993；Simpson et al.，1997；Ferreira and Schubert，1997；Kieu and Zhang，2009；Yu et al.，2010；Jang and Chun，2015）.At the smaller convective scales，coalescence of deep convective towers in the atmosphere—the so-called vortical hot towers—has been recently suggested as a pathway for the upscale growth of tropical depressions during the early phase of tropical cyclogenesis［“the vortical hot towers hypothesis”，e.g.，Montgomery and Enagonio（1998）and Hendricks et al.（2004）］.

Despite extensive numerical studies on the vortex merging process for a wide range of scales，it is nevertheless intriguing that the process of merging vortices has never been precisely defined.Specifically，it is not clear in general if the process of merging multiple vortices into a single vorticity patch can be fully complete at the end of the vortex interaction，or if the final circulation must be enhanced as a result of the vortex merger.For example，modeling studies of vortex merger by Dritschel and Waugh（1992），Prieto et al.（2003）and Kuo et al.（2008）revealed that the merger depends on the strength of each different vortex，the distance between the vortices，and the relative size of the vortices.In all cases，the full vortex merger does not appear to be realized，even for cases that belong to the complete merger category.

In this study，the vortex merging process is investigated for a special class of 2D flows that is barotropic and inviscid，and the necessary conditions for the merger to be considered complete at the end of the merging process are examined. The approach is based essentially on the unique characteristics of the barotropic vorticity equation，which allow for rigorous analyses of the vorticity dynamics under some specific boundary conditions.While these analyses are strictly valid only for the inviscid barotropic dynamics，due to some technical constraints that may not be applicable to more general vortex merging processes，the modest aim in this study is to present an approach that could highlight the subtlety of the vortex merging and interpretation that has not been adequately addressed in previous studies.

The rest of the paper is organized as follows.The nextsection introduces a definition for a complete vortex merger intheframeworkofthebarotropicflows.Analysesofthevorticity dynamics and the evolution of the merging processes are then presented in detail under different boundary configurations.Some concluding remarks are given in the final section.

©Institute of Atmospheric Physics/Chinese Academy of Sciences，and Science Press and Springer-Verlag Berlin Heidelberg 2016

2.Barotropic dynamics

2.1.Vortex merger definition

Although vortex merging processes in both 2D and 3D flows have been extensively demonstrated in numerous modeling studies，the fact that the merging varies strongly with different scales and dynamical systems renders it difficult to understand whether and how the merging process really occurs.Depending on the relative size and distances between vortices，a study of the vortex merging in Dritschel and Waugh（1992）showed that there are generally five different flow regimes at the end of the merging，which include（1）elastic interaction，（2）complete merger，（3）partial merger，（4）partial straining out，and（5）complete straining out for the 2D flows.Such a classification of merging processes was later investigated in many numerical experiments（e.g.，Yasuda，1995；Prieto et al.，2003；Kuo et al.，2008），which confirmed these regimes systematically in both the barotropic and 3D framework.

Following the innovative contour dynamics approach presented in Dritschel and Waugh（1992），a quantitative criterion to classify the vortex merging process for mesoscale atmospheric flows was introduced in Prieto et al.（2003）and Kuo et al.（2008），which is based on the ratio of the final to the initial circulation for each participating vortex；the circulation ratio is equal to 1 for complete merger，and zero for elastic interaction.Such a definition of vortex merger based on global contour circulation has the benefit of efficiently removing filamentary structures and isolating coherent vorticity patches，but it subjectively depends on how one defines the contours around which the circulation can be computed，as mentioned in Dritschel and Waugh（1992）.This explains why the complete merger regime in Prieto et al.（2003）and Kuo et al.（2008）does not really exhibit the complete merging of two vortices into a single vorticity patch at the end of the merging process，but instead displays a spread of one vortex in the form of vorticity skirts wrapping around the other vortex［e.g.，Prieto et al.（2003，Fig.2a）and Kuo et al.（2008，Fig.9）］.

Given the lack of a rigorous definition for the vortex merging process，which is needed to better define and understand the evolution of the vortex dynamics，this subsection begins by first redefining the merging process from a barotropic flow perspective，to facilitate subsequent analyses of the vortex merger.Note a specific property that one would expect from a complete vortex merging process is that the end product of a merging process should be a stationaryaNote that the“stationary”criterion by no means implies that the flow has to completely stop.It just means that the final state of the flow is not an explicit function of time.vortex，which would not evolve by itself or break down at all later time.This condition is necessary so that it can at least be agreed whether or not the vortex merger is complete.One could relax this condition by allowing for cases with some type of periodic oscillation instead of a stationary vortex patch at the end of the vortex merger.However，as shown in the next section，certain configurations in the barotropic framework do not even approach an equilibrium with a single vortex patch at the end of the merging，let alone oscillating around an equilibrium.The aim in this subsection is to express such a stationary merger condition more quantitatively，and use this condition to examine how and when the vortex dynamics will approach the stationary limit.

To present the characteristics of vortex merging in an analytically tractable manner，let us start first with the inviscid barotropic equation in an f-plane（see Holton，2004）as follows:

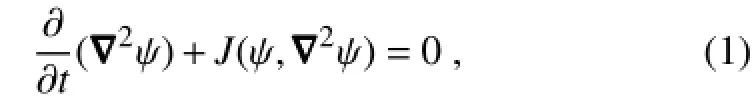
where ψ（x，y，t）is assumed to be at least a real squareintegrable functionbTechnically，the set of all real square-integrable functions f（x）is called L2-space，defined as L2（Ω）=（f: Ω→R|ʃ|f（x）|2dx＜∞）.over a given domain Ω∈R2.Equation（1）accepts a stationary solution Ψ（x，y）if

or equivalently

A symmetry in the x and y derivatives in Eq.（2）immediately suggests that this equation will be generally satisfied if the following relationship holds:

where λ is an eigenvalue.Equation（3）is familiar and indicates that the stationary solution Ψ（x，y）is nothing but an eigenfunction of the Laplacian operator Δ.The existence of such a stationary solutioncStationary solutions for the streamfunction mean that vortex flows are purely advective.is of key importance for studying barotropic vortex evolution，because if the complete merging of multiple vortices can indeed take place，then one would expect eventually that the final state of the vortex dynamics would settle down to some“stable”configuration，which is exactly what a stationary solution is supposed to be.For most applications in the atmosphere，it suffices to assume also that the streamfunction on Ω has a compact support such that the Laplacian operator Δ is self-adjoint（i.e.，〈Δf，g〉=〈f，Δg〉），where f and g are two arbitrary smooth functions defined on Ω.This ensures that the eigenvalues of the Laplacian are all positive，0＜λ1＜λ2＜λ3＜···，and the corresponding eigenfunctions｛φ1，φ2，φ3，···｝form an orthogonal basis according to the Spectral Theorem（Nica，2011）.

It should be noted that，strictly speaking，the pure eigenfunctions of the Laplacian operator are not the most general stationary solution of Eq.（2）.However，given the fact that the spectrum of the Laplacian eigenfunctions are complete for homogeneous boundary conditions from the Spectral Theorem，any stationary solutions with the same boundary condition will therefore have to be a superposition of the Laplacian eigenfunctions.As such，examining the characteristics of the Laplacian eigenfunctions can provide insights into general long-term behaviors of the stationary solutions of the barotropic vorticity equation［Eq.（1）］.

With well-established properties of the eigenfunctions of the Laplacian operator，it is apparent that there are an infinite number of stationary states for the barotropic vorticity equation；each corresponds to one eigenfunction of the Laplacian operator.For a circle domain Ω，an eigenfunction φk，λ（θ，r）corresponding to an eigenvalue（λ，k）is given by（e.g.，Canzani，2013）:

where ak，bkare constants，θ is the azimuthal coordinate variable，and Jk（x）is the k-order Bessel functions defined as follows:

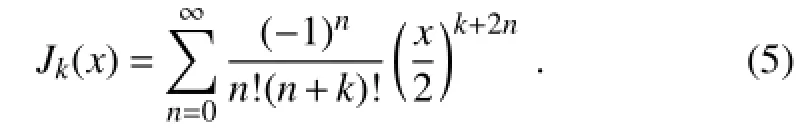
As seen in Fig.1，these eigenfunctions display a wide range of shapes，depending on the value of the radial eigenvalue λ and the azimuthal eigenvalue k.For a typical vortex merging problem that is expected to settle down towards a stationary state，we note however that it is the eigenfunction with no θ-dependence，i.e.，any eigenmode with k=0，that is most anticipated at the end of the vortex merger.This is because these k=0 states are the only configurations that possess a vortex concentrated at the domain center and diminishes radially outwards（assuming that one can always arrange the domain in such a way that an initial vortex distribution has its mass-weighted vorticity center located at the domain center）.Any other configuration with k≠0 would correspond to a distribution of positive vorticity centers located at different places，which are not expected for the“complete”vortex merging from the symmetry perspective.

The above observation of the radial symmetry of the eigenfunctions thus allows us to precisely define conditions for a complete merging process.Assume one starts with an arbitrary distribution of vorticity on a domain Ω with a null boundary condition for which the streamfunction ψ（r，θ，t）can be expanded as follows:

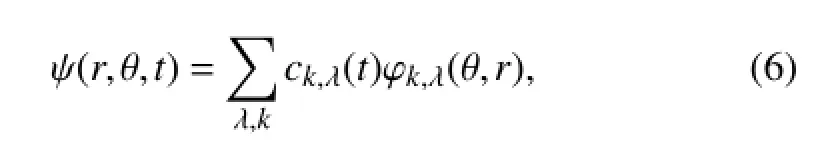
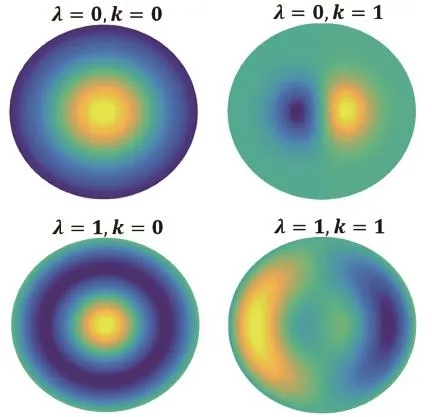
Fig.1.Illustration of the eigenfunctions φk，λ（θ，λ）of the Laplacian operator with different values of λ and k.

where ck，λare expansion coefficients.It is then clear that the evolution of the barotropic flow under the governing equation［Eq.（1）］will eventually approach a stationary axisymmetric configuration if the following conditions hold:Indeed，if these conditions are satisfied after a sufficiently long period of time，then the merging process can be claimed as complete because the flow settles down to a specific superposition of stationary axisymmetric eigenfunctions with a resulting vortex located at the center.Such a complete merger will directly support the assumption of aggregating multiple like-signed vortices，as often assumed in previous studies of vortex interaction.We should mention that the condition represented by Eq.（7）by no means dictates that the end phase of the merging process has to be exactly an eigenfunction of the Laplacian operator.The final vortex could in fact be a superposition of infinite eigenfunctions φ0，λ（θ，λ），provided that the superposition ensures a peak vorticity at the center to meet with the expectation of a complete vortex merger. The problem will be much less flexible for different boundary conditions or different domain topologies.Nonetheless，the existence of an orthogonal basis that corresponds to eigenfunctions of the Laplacian operator gives us a unique way to shed light onto these merging processes in some specific applications，at least from the barotropic flow perspective，to which the focus turns next.

2.2.Vortex merging in a square domain

In this section，the above definition of the complete vortex merger is applied to examine the vortex dynamics in a limited-area domain.The objective in this subsection is to investigate how an arbitrary distribution of vorticity at the initial time in a square domain would evolve and under what conditions the merging process can be considered complete，as defined by the complete merger conditions［i.e.，Eq.（7）］. To approach the problem of modeling the vortex dynamics in as practical a way as possible，a specific square domain［0，L］×［0，L］with periodic boundary conditions is hereinafter considered，where L is a given domain size.The compactsupport requirement to ensure the self-adjoint property of the Laplacian operator puts a strong constraint on the set of the eigenfunctions of Eq.（3），which are now given for each specific mode（m，n）as follows: Figure 2 illustrates the first few eigenfunctions φm，n（x，y）.Unlike a circular disk domain that can support many axisymmetric eigenmodes toward which the barotropic flow could approach at the end of the vortex merger，the only mode that possesses the maximum vorticity at the center of the square domain is m=1，n=1.Based again on the symmetry argument，the conditions for a vortex merging process to be complete in a square domain are thus reduced to

These conditions［Eq.（9）；hereinafter referred to as the complete merger condition for the square domain］are used to examine how an initial distribution of vorticity will evolve and eventuallyapproachthestationaryeigenmode（1，1）attheend of the merging process.It should be mentioned again that both sets of conditions［Eqs.（7）and（9）］are in fact“strong conditions”for a complete vortex merger.This is because someinfinite superposition of coefficientscm，nmayexistsuch that the final function could possess a radially axisymmetric distribution，mimicking a stationary end product of the vortexmerging.It will be shown below，however，that the dynamics of the barotropic flows in the square domain possesses very specific characteristics，which do not admit such an arbitrary superposition of general eigenmodes.

Fig.2.Illustration of eigenfunctions φm，nin a square domain with periodic boundary conditions for several different values of（m，n）.

To this end，recall first that the completeness of the orthogonal eigenfunctions［Eq.（8）］over the square domain allows us to expand an arbitrary streamfunction ψ（x，y，t）as follows:

Substituting the solution of Eq.（10）into Eq.（1），we have

where the dummy integer indices（m，n）and（k，l）have been interchanged in the second term on the right-hand side of Eq.（11）to facilitate later grouping.Multiply both sides of Eq.（11）by an eigenfunction φM，Nthat corresponds to a specific mode（M，N）and integrate both sides with respect to x and y over the entire domain with a note that

where δm，nis the delta Kronecker symbol，we arrive at a governing equation for each eigenmode（M，N）after some rearrangement as follows:

It can be seen from Eq.（14）that if one starts with any specific eigenfunction（K，L），then dcm，n/dt=0，∀m，n＞0，and the flow will stay at the same initial mode（K，L）at all times，as expected for stationary solutions.Note also that the evolution of each mode（M，N）is strongly coupled to other modes via the double summation over（m，n）and（k，l）on the righthand side of Eq.（14）.As such，the vortex dynamics is inherently nonlinear.

A couple of remarks can be immediately obtained from Eq.（14）.First，the symmetry of the（m，n）and（n，m）modes in Eq.（14）suggests that an initial distribution of vorticity composed of exactly two eigenmodes（K，L）and（L，K），where K，L are any two integer numbers，will not evolve with time.This is because the forcing term on the righthand side of Eq.（14）will be reduced to only terms of the form～（δK，L-δL，K），or～（δK，L-δK，L），which are all canceled out because of λm，n=λn，m，and so dcM，N/dt=0，∀M，N. While this property depends crucially on the square topology of the domain，it highlights a subtle characteristic of the multiple vortex interaction.Imagine one starts with a vorticity distribution consisting of two specific amplitude modes c9，10=1 and c10，9=1，which resembles a set of small-scale like-signed vorticity centers as shown in Fig.3.The gross overall picture of multiple like-signed vorticity centers may provide one with some intuitive feeling that these like-signed vortices may soon interact，merge，and grow upscale.As seen above，such a vortex merger could not，however，take place；the entire vorticity distribution simply stays the same without any evolution or interaction at all.

Fig.3.Distribution of nondimensionalized streamfunction（shaded），which is composed of exactly two eigenmodes，（9，10）and（10，9），with amplitudes c9，10=-1 and c10，9=-1.

Of further importance is an observation about the delta Kronecker symbols on the right-hand side of Eq.（14）for which the subscripts are always combinations of either k±m or l±n.This property dictates that if one starts with an initial vorticity distribution containing either purely even modes（i.e.，both k and m are even）or purely odd modes（i.e.，both k and m are odd）in one specific direction（either x or y），then the subsequent evolution will involve either entirely even modes or odd modes in that direction only.This is a direct consequence of the selective Kronecker delta for which the odd superscripts M or N can never be equal to thecombination of purely even or odd subscripts m，k or n，l，which are always even numbers.For example，if the initial vorticity distribution is given by several even modes along the x direction consisting of（m=2，n-1），（m=4，n=5），and（m=6，n=7），the flow will then quickly spread out over all other even eigenstates along the x direction，as can be seen from Eq.（14），whereas all of the odd eigenstates along the x direction will never appear.In particular，this shows that the most important eigenstate expected for the complete merger condition（m=1，n=1）will never be satisfied（i.e.，limt→∞c1，1≠0 cannot occur）despite the strong interaction of vortices.As such，the complete merger condition［Eq.（9）］is not ensured，and the vortex merging process will never end up in a single vortex patch at the center as one would expect from the complete vortex merging process.

As an illustration of the above particular selective property of the Kronecker operator，Fig.4 shows the evolution of the streamfunction and the corresponding horizontal wind components u=-∂ψ/∂y and v=∂ψ/∂x，obtained from a numerical integration of Eq.（14）.Here，the numerical experiment is carried out for a square domain［0，1000 km］×［0，1000 km］on an f-plane located at 30°N，with homogeneous boundary conditions and an initial condition consisting of three eigenmodes of c10，10=1，c12，12=1，and c14，14=1，where the amplitudes are scaled by a factor L2f.A spectrum truncation of 30 normal modes is applied in both the x and y directions，and the integration time-step is fixed at 120 s.

One notices in Fig.4 that，clearly，despite strong evolution of the vortex patches with time，there is no global merger of like-signed vortices.In fact，the initial condition consisting of the above selected even modes results in a complete cancellation of the wave amplitudes at the center of the domain，such that there is no way for the vorticity centers to aggregate at the center of the domain；all vortex merging can only take place locally，away from the domain center，and the complete merger with a single vortex patch at the domain center never occurs.While the merging of the vorticity cannot be aggregated toward the center of the domain，note that multiple vortex mergers could take place elsewhere，which is seen by the development of several major patches of vorticity in four quadrants shown in Figs.4c—e.Such self-organization of small-scale vortices is consistent with the concept of“vortex relaxation”into large-scale structures due to minimization（or maximization）of potential intrinsic invariants of the barotropic fluid such as enstrophy，energy，or helicity（e.g.，Brown，1997）.However，the type of largerscale vorticity patches shown in Figs.4b and c does not grow upscale indefinitely，but instead breaks down subsequently，as seen in Fig.4f.The processes of vortex merging and breaking down take place around 2000 time-steps.One can in principle increase the degree of vortex interaction by either using a larger wave amplitude to increase the vortex strength，or selecting higher wavenumbers to reduce the distances between like-signed vortices.Nevertheless，a complete vortex merger with relaxation towards a single stationary vortex at the domain center could not take place due to the selective mode of the barotropic dynamics.Of course，the vortex merging process seen in Fig.4 is particularly inherent to the inviscid barotropic model，and it will change entirely if diffusion forcings or higher dimensions are introduced.However，this barotropic merging process could demonstrate the intricate dynamics that a simple merging scenario for like-signed vortices may not always apply.

It is worth emphasizing that，unlike the superposition of two symmetric states，which leads to stationary dynamics due to the topology of the square domain shown in Fig.3，the evolution of either purely even or odd eigenstates illustrated in Fig.4 is a general property of the governing equation［Eq.（14）］related to the completeness of the eigenfunctions φm，n. In fact，this selective property of the Kronecker symbols has an even stronger implication，as it essentially eliminates any possibility of superimposing arbitrary eigenfunctions φm，nto obtainastationaryGaussian-likestateforthecompletevortex merger.To the best of the author’s knowledge，no superposition of purely even or odd sinusoidal modes along the x or y direction has been known that could produce a Gaussian-like profile for vorticity at the domain center to mimic the complete merger expectation.From this perspective，the unique selective property of Eq.（14）suggests that simple intuition regarding the merging of like-signed vortices should be taken with caution，as it may not be applicable.

Except for the above special characteristics of Eq.（14）that result in either strictly stationary states or interaction among eigenmodes in some selective way，an arbitrary vorticity arrangementwill overallbe distributed acrossthe whole spectrum of eigenfunctions quickly with time，and it seems to have no stationary end state as one would expect for the complete merger.For the sake of discussion，consider an arbitrary initial field ψ（x，y，0）that consists of only three eigenstates of（m=1，n=1），（m=1，n=2）and（m=2，n=1）（i.e.，c1，1（0）≠0，c1，2≠0，and c2，1（0）≠0），which roughly correspond to a vortex at the center of the domain surrounded by two lumps of vorticity along its x and y direction.The purpose is to see if the superposition of these three eigenstates in this example could eventually become a single stationary mode of（m=1，n=1）that represents a resulting merged vortex.More general distribution of ψ（x，y，0）can be similarly examined along the same line of argument.Given such an initial condition，Eq.（14）gives us a sequence of spectral evolution shown in Table 1.As seen in Table 1，the strong nonlinear coupling of all eigenstates in Eq.（14）leads to rapid expansion of the flow over many other eigenstates after just a few time steps.If one continues the integration of Eq.（14）further in time，the entire eigenfunctions spectrum would be occupied quickly，and there appears to be no simple setup to guarantee that the complete merger condition［Eq.（9）］could be ensured in general.

Fig.4.Snapshots of the nondimensionalized streamfunction ψ（shaded）and the corresponding horizontal wind components（u，v）（vectors）on an f-plane located at 30°N，which are valid at t=0 h，t≈6.5 h，t≈13 h，t≈19.5 h and t≈27 h，which correspond to 0，200，400，600，800 and 1000 time-steps into the integration，using Eq.（14）.

It is of interest to mention that the rapid distribution of barotropic flow over the whole eigenfunction spectrum can also be applied for the β-plane vorticity equation due to the orthogonality of the eigenfunctions φm，n.As discussed in Yasuda（1995），the β-effects will，however，complicate the vortex merging process by creating asymmetry of the vortex merging along the south—north direction，and the vortex merger becomes even less complete.In particular，Prieto et al.（2003）showed that inclusion of the β-effect can significantly slow down the mutual rotation between two vortices，as the Coriolis forcing is weaker at higher latitudes，thus lengthening the merging process.These details are hard to formulate from the analytical perspective，because the stationary states may not exist for the β-plane dynamics.However，the completeness of the eigenfunctions φm，nstill at leastmerger conditions［Eq.（9）］for the barotropic dynamics as given by Eq.（1），and so it is more likely that the complete vortex merging processes may never occur in the sense of the complete merger condition［Eq.（9）］.allows for the expansion［Eq.（10）］，and therefore the spread of the eigenfunction spectrum as seen for the f-plane dynamics can still be valid.This continuous spread over the whole eigenfunction spectrum appears to explain the formation of vorticity skirts wrapping around the other vortex instead of a single enhanced circulation seen at the end of the complete vortex merger case，as presented in Prieto et al.（2003）and Kuo et al.（2008）.

Table 1.Developmentofneweigenmodesφm，nforthefirstfourtime steps every 2 min，using Eq.（14）with initial conditions consisting of three modes of c1，1，c1，2，and c2，1at a truncation of 20 wavenumbers（i.e.，m，n＜20）.

It should be noted that the spread of the eigenmodes over the spectrum of the Laplacian eigenfunctions does not sufficiently imply that the vortex merging will never take place for all configurations.It is still possible that，as time goes on，the flow may evolve in such a way that cm，n→∈，∀m，n≠1，where∈is an arbitrarily small number，such that，practically，one may no longer be able to notice any other modes except for the dominant mode of（m=1，n=1）from a numerical viewpoint.For these situations，it is reasonable to state that these higher wavenumber modes diminish to a point that the merging is considered to be practically complete.While such an argument could be applied from the numerical standpoint，apparently it requires one to define carefully how small a perturbation would be so that it can be numerically neglected. To the best of the author’s knowledge，there is no known configuration at present that could strictly ensure the complete

3.Concluding remarks

This study analyzes the 2D vortex dynamics governed by the inviscid barotropic vorticity equation.By noting that the Jacobian operator in the vorticity equation of the form J（ψ，∇2ψ）accepts a set of stationary solutions that are inherently eigenfunctions of the Laplacian operator，it is found that the vortex evolution can be decomposed into a set of spectral components that evolve according to a system of highly nonlinear constraints.Given the specific shapes and characteristics of the eigenfunctions of the Laplacian operator with a prescribed boundary，it is shown that sufficient conditions exist for the vortex merging process to be considered strictly complete.

Examination of the vortex dynamics for a square domain with periodic boundary conditions shows that，unlike the common expectation of merging of like-signed vortices，the complete merger is not guaranteed for an arbitrary initial distribution of vorticity.In fact，it is demonstrated that there are certain initial combinations of vorticity that the complete vortex merger condition can never be satisfied.Specifically，the superposition of eigenmodes that are purely even or odd in either the x or y direction will lead to an evolution that contains only even modes in either the x or y direction at all times，regardless of how close and strong like-signed vortices are.In a more extreme case with two symmetric sinusoidal modes，the dynamics is even strictly stationary，and no vortex merging would take place.Analyses of the more general cases also suggests that an arbitrary vorticity distribution at the initial time would quickly spread out over the whole spectrum of the eigenfunctions of the Laplacian operator，and there is no guarantee that modes with higher wavenumbers would diminish in time such that the flow would settle in a final state with a single vortex patch at the center of interaction.

It is important to note that the results obtained in this study are very specific for inviscid barotropic fluid，and by no means encompass the full range of vortex interactions.In particular，the strict definition of the complete vortex merger，as given by either the condition for a circular domain［Eq.（7）］or a square domain［Eq.（9）］，is too strong such that no configuration may exist for the complete vortex merger to occur.In practice，it is possible that the vortex dynamics in a 3D space or inclusion of viscosity may allow for a complete merger and subsequent upscale growth of the resulting vortex（Kieu and Zhang，2009；Huang and Xu，2010；Luo et al.，2014）.However，the barotropic model in this study suffices to demonstrate that an intuitive notion of merging of like-signed vortices，which is often assumed in studies of multiple vortex interaction，is highly intricate and should be taken with caution，as the vortex merger may not lead to an eventually enhanced circulation as one would expect.

Acknowledgements.The author would like to thank Dr. Shouhong WANG（Indiana University）for his general comments and suggestions，and Dr.David SCHECTER for his discussion on the vortex relaxation into large-scale structures.Thanks are also extended to the two anonymous reviewers，whose comments and suggestions have helped improve this work significantly.This research was supported by Indiana University start-up funding.

REFERENCES

Brown，M.R.，1997:Experimental evidence of rapid relaxation to large-scale structures in turbulent fluids:Selective decay and maximal entropy.Journal of Plasma Physics，57，203—229.

Canzani，Y.，2013:Notes for analysis on manifolds via the Laplacian.Harvard University.［Available online at http://www. math.harvard.edu/～canzani/docs/Laplacian.pdf.］

Cerretelli，C.，and C.H.K.Williamson，2003:The physical mechanism for vortex merging.J.Fluid Mech.，475，41—77.

Dritschel，D.G.，and D.W.Waugh，1992:Quantification of the inelastic interaction of un-equal vortices in two-dimensional vortex dynamics.Physics of Fluids A:Fluid Dynamics，4，1737—1744.

Ferreira，R.N.，and W.H.Schubert，1997:Barotropic aspects of ITCZ breakdown.J.Atmos.Sci.，54，261—285.

Hendricks，E.A.，M.T.Montgomery，and C.A.Davis，2004:The role of“Vortical”hot towers in the formation of tropical cyclone Diana（1984）.J.Atmos.Sci.，61，1209—1232.

Holton，J.R.2004:An Introduction to Dynamic Meteorology.4th ed.，Academic Press，535 pp.

Huang，H.M.，and X.-L.Xu，2010:Simulation on motion of particles in vortex merging process.Applied Mathematics and Mechanics，31，461—470.

Jang，W.，and H.Y.Chun，2015:Characteristics of binary tropical cyclones observed in the Western North Pacific for 62 years（1951—2012）.Mon.Wea.Rev.，143，1749—1761.

Josser，C.，and M.Rossi，2007:The merging of two co-rotating vortices:A numerical study.European Journal of Mechanics-B/Fluids，26，779—794.

Kieu，C.Q.，and D.L.Zhang，2009:Genesis of tropical storm Eugene（2005）from merging vortices associated with ITCZ breakdowns.Part II:Roles of vortex merger and ambient potential vorticity.J.Atmos.Sci.，67，1980—1996.

Kuo，H.C.，W.H.Schubert，C.L.Tsai，and Y.F.Kuo，2008:Vortex interactions and Barotropic aspects of concentric eyewall formation.Mon.Wea.Rev.，136，5183—5198.

Lander，M.，andG.J.Holland，1993:Ontheinteractionoftropicalcyclone-scale vortices.I:Observations.Quart.J.Roy.Meteor. Soc.，119，1347—1361.

Lansky，I.M.，T.M.O’Neil，and D.A.Schecter，1997:A theory of vortex merger.Physical Review Letters，79，1479—1482.

Luo，D.H.，J.Cha，L.H.Zhong，and A.G.Dai，2014:A nonlinear multiscale interaction model for atmospheric blocking:The eddy-blocking matching mechanism.Quart.J.Roy.Meteor. Soc.，140，1785—1808.

Montgomery，M.T.，and J.Enagonio，1998:Tropical cyclogenesis via convectively forced vortex Rossby waves in a three-dimensional quasigeostrophic model.J.Atmos.Sci.，55，3176—3207.

Nica，M.，2011:Eigenvalues and Eigenfunctions of the Laplacian，The Waterloo Mathematics Review，1，23-34.

Prieto，R.，B.D.McNoldy，S.R.Fulton，and W.H.Schubert，2003: A classification of binary tropical cyclone-like vortex interactions.Mon.Wea.Rev.，131，2656—2666.

Rodr´ıguez-Marroyo，R.，´A.Vi´udez，and S.Ruiz，2011:Vortex merger in oceanic tripoles.J.Phys.Oceanogr.，41，1239—1251.

Simpson，J.，E.Ritchie，G.J.Holland，J.Halverson，and S.Stewart，1997:Mesoscale interactions in tropical cyclone genesis. Mon.Wea.Rev.，125，2643—2661.

Tallapragada，V.，C.Kieu，2014:Real-Time Forecasts of Typhoon Rapid Intensification in the North Western Pacific Basin with the NCEP Operational HWRF Model.Tropical Cyclone Research and Review，3，63-77.

Wang，C.-C.，and G.Magnusdottir，2006:The ITCZ in the central and eastern Pacific on synoptic time scales.Mon.Wea.Rev.，134，1405—1421.

Yamazaki，A.，and H.Itoh，2013:Vortex—vortex interactions for the maintenance of blocking.Part I:The selective absorption mechanism and a case study.J.Atmos.Sci.，70，725—742.

Yasuda，I.，1995:Geostrophic vortex merger and streamer development in the ocean with special reference to the merger of Kuroshio warm core rings.J.Phys.Oceanogr.，25，979—996.

Yu，Z.F.，X.D.Liang，H.Yu，and J.C.L.Chan，2010:Mesoscale vortex generation and merging process:A case study associated with a post-landfall tropical depression.Adv.Atmos.Sci.，27，356—370，doi:10.1007/s00376-009-8091-x.

Kieu，C.，2016:Thedynamicsofbarotropicvortexmerging.Adv.Atmos.Sci.，33（8），987—995，

10.1007/s00376-016-6006-1.

（7 January 2016；revised 26 March 2016；accepted 25 April 2016）

Chanh KIEU

Email:ckieu@indiana.edu