LYU Jian-Qiu, WANG Hong-Qi

Abstract In this paper,we study the consensus problem for multi-agent systems under a directed graph.First,the velocity-free consensus algorithm for double-integrator dynamics is proposed,in which the graph theory and Lyapunov stability theory are applied.The proposed consensus algorithm guarantees that the states of all agents can reach consensus asymptotically.Then,the obtained results and techniques are extended to the attitude consensus for multiple rigid bodies.Numerical simulations are given to validate the effectiveness of the proposed method.

Key words consensus,cooperative control,multi-agent systems

The consensus problem of multi-agent systems has attracted attention from researchers in recent years.Various approaches have been proposed to investigate the consensus problems of second-order multi-agent systems[1−10].A practical research topic for second-order multi-agent systems is velocity immeasurements problem because velocity information is not always available.Hence the study of consensus for multi-agent systems without velocity information is very interesting.

In[11],authors give consensus algorithm for doubleintegrator dynamics under an undirected graph without velocity measurements and show that consensus is reached asymptotically.In[12],authors developed the consensus algorithms for double integrator multi-agent systems in the case where the inputs are bounded and the velocity information are not available for feedback.Authors in[13]propose bounded and velocity-free algorithms to achieve consensus for heterogeneous multi-agent system.In[14],the authors consider the consensus problem of the heterogeneous multi-agent system with agents modeled by firstorder and second-order integrators,and propose finite-time consensus algorithms for the system with and without velocity measurements.A new class of observer-based control algorithms are designed for achieving finite-time consensus tracking in multi-agent systems with a single active leader and multiple active leaders in[15].

Consensus for nonlinear multi-agent systems,especially the multiple rigid bodies whose attitude motion equation can be expressed by Euler-Lagrange equations,has also received much research interest.The coordinated attitude control algorithms for multiple rigid bodies are proposed in[16].The distributed robust finite-time attitude containment control problems for multiple rigid bodies with uncertainties are studied in[17].Authors in[18]proposed a passivity approach for distributed attitude synchronization for multiple rigid bodies without angular velocity measurements.Authors in[19]studied the attitude synchronization problem of multiple rigid bodies with communication delays and without angular velocity information.Author in[20]proposed two distributed control schemes to solve the attitude synchronization and tracking problem for multiple rigid bodies in undirected networks and the angular velocity measurements are only required in the first control scheme.

The main purpose of this paper is to study consensus problem for multi-agent systems under a directed graph without velocity measurements.We first investigate the consensus problem for double-integrator agents systems.The proposed consensus algorithm allow to generate the inputs which area prioribounded and guarantees asymptotical convergence while removing the requirement on the velocity measurements.Then we extend the obtained results and techniques for double-integrator agents to multiple rigid bodies to achieve attitude synchronization.

The rest of the paper is organized as follows. Some preliminary results are presented in section 1.In sections 2,we give the velocity-free consensus algorithm for multiagent systems under a directed graph.Numerical simulation is provided to validate the performance of the proposed method in section 3.Finally,concluding remarks are given in section 4.

1 Preliminaries

Suppose that every agents have double-integrator dynamics given by

wherexi(t)∈R,υi(t)∈R andui(t)∈R are the position,velocity and control input,respectively,of agenti.

Using graph theory,we can model the network topology in a multi-agent system consisting ofnagents.A graphGconsists of a node setV={1,···,n},an edge setE⊆V×V,and a weighted adjacency matrixA=[aij]∈Rn×nwith weightsaij>0 if(j,i)∈Eandaij=0 if otherwise.GraphGis undirected if for any edge(i,j)∈E,we have(j,i)∈E.A path from nodeito nodejis a sequence of edges in a graph.A directed graph is strongly connected if there is a directed path from every node to every other node.A undirected graph is called connected if there is a path between every pair of nodes in a undirected graph.

2 Consensus algorithms design

In this section,we consider the consensus problem without velocity measurements for double-integrator dynamics under a directed graph.Assume that graphGsatisfies the detail-balanced condition that there exist some scalarsµisuch thatµiaij=µjajifor alli,j∈V.

Letm=1,2,cm>0,andψmis odd function satisfyingyψm(y)>0 andψm(y)=cmy+o(y),asy→0,the following consensus protocol is proposed as

wherekiandλiare positive constants,andaijis the(i,j)th entry of the weighted adjacency matrixA.

Theorem1.Consider the system(1)with protocol(2)−(3).If directed graphGis detail-balanced and strong connected,thenxi(t)→xj(t),υi(t)→υj(t)asymptotically.

Proof.See Appendix A.

We can also consider the case of an undirected communication topology and assume that the undirected graphGis connected.Then we have the following result.

Corollary1. Consider the system(1)with protocol(2)−(3). If the undirected graphGis connected,thenxi(t)→xj(t),υi(t)→υj(t)asymptotically.

Remark1.If we chooseψias bounded functions,then we have consensus protocol in saturation form

For system(1)with consensus protocol(4)and(5),if control gains satisfy

then|ui|≤umi,whereumidenotes the maximum allowable control input.

Remark2.The following velocity-free consensus protocol can also guarantee consensus

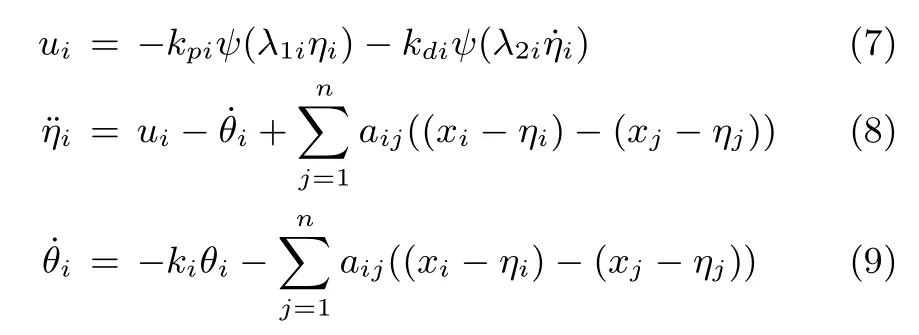
wherekpi,kdi,ki,λ1iandλ2iare positive constants.From(7),it is clear that the bounds of the control input of the consensus protocol did not depend on the number of neighbors of each agent compared with(2)when we chooseψias bounded functions.

Remark3.Note that the proposed velocity-free control idea here work for attitude consensus problem for multiple rigid bodies as well.The attitude kinematic and dynamic equations of theith rigid body are given as

whereωi∈R3is the angular velocity of theith rigid body in the body frame;Ji∈R3×3is the inertia tensor;ui∈R3is control torque;σi∈R3is the modified Rodrigues parameters of theith rigid body;Gi(σi)is given by

The control algorithm is designed as wherekdi,λi,βiandkiare positive constants.

Theorem2.Consider the system(10)−(11)and the control algorithm(12)−(13).If directed graphGis detailbalanced and strong connected,thenσi→σjandωi→0 asymptotically.

Proof.See Appendix B.

Corollary2.Consider the system(10)−(11)and the control algorithm(12)−(13).If the undirected graphGis connected,thenσi→σjandωi→0 asymptotically.

Remark4.It can be seen that the following control algorithm can also guarantee attitude consensus

whereλi,βiandkiare positive constants.

From(14),it is clear that control algorithm is dependent of the angular velocity information compared with(12)−(13).

Remark5.It can be easily checked that the control law is bounded byif we chooseψ(y)=tanh(y).Hence,||ui||≤umifollows from the condition

3 Simulation results

In this section,we give some numerical simulation results to illustrate the effectiveness of the theoretical results obtained in this paper.The communication topology between agents is represented by he graphG,withV={1,···,6}andE={(1,2),(1,3),(2,5),(3,5),(5,6),(4,6)}.The inertia matrices are given asJi=[42 1.8−1.5;1.8 26−1.2;−1.5−1.262]kg·m2.

We first consider the control algorithm(2)∼(3)withki=0.25 andλi=1.The results of the simulation are shown in Figs.1∼3.It can be seen that consensus can be achieved without velocity measurements.

Fig.1 Positions of all agents

Fig.2 Velocities of all agents

Fig.3 Control input of all agents

Then,we consider the control algorithm(12)∼(13)withλi=1,kdi=0.6,ki=25 andβi=0.1.The results of the simulation are shown in Figs.4∼6.It can be seen that attitude consensus can be achieved without angular velocity measurements.

4 Conclusions

In this paper,the consensus problem is studied for multiagent systems.We develop a velocity-free algorithm under directed graph and show that consensus can be reached asymptotically.Then a attitude synchronization control algorithm is proposed for multiple rigid bodies without angular velocity measurements.In our future work,we will develop the evolutionary game theoretic approach to cooperative control of multi-agent systems.

Fig.4 Attitudes of all rigid bodies

Fig.5 Angular velocities of all rigid bodies

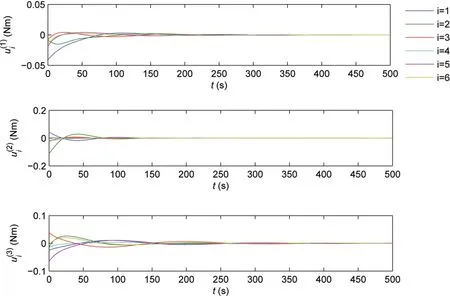
Fig.6 Control torques of all rigid bodies

APPENDIX A

PROOF OF THEOREM 1

Consider the Lyapunov function candidate

The time derivative ofVis giving by

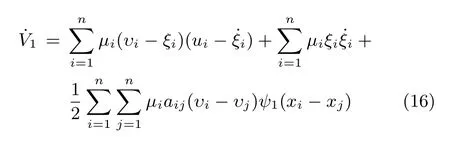
From(2)∼(3),we have that

which is negative semi-definite,and we can conclude thatξi,υiandxi−xjare globally bounded.We can see from(3)thatis bounded.Therefore we know thatis bounded.Then from Barbalat Lemma we can conclude thatIn addition,sinceandυiis bounded,we know thatis bounded,and since we have already shown thatwe know by Barbalat Lemma thatTherefore,we conclude that

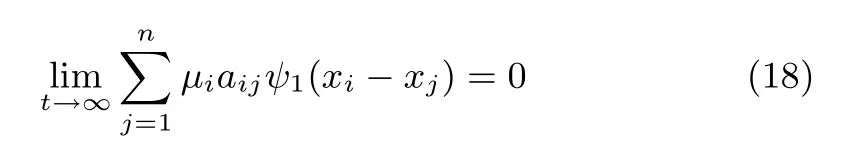
It follows that

Therefore,we can conclude thatif the directed graphGis strong connected.From Barbalat Lemma we can conclude that

APPENDIX B

PROOF OF THEOREM 2

The equations(10)∼(11)can be expressed in the Euler-Lagrange formulation as

Consider the Lyapunov function candidate

The time derivative ofVis giving by

Using(10)and the fact that(˙Mi−2Ci)is skewsymmetric,we obtain

Similar to the analysis of Theorem 1,we can conclude thatThen from(13)and(10)we can conclude thatFinally we can conclude that