Yangyang Yu，Linlin Wang，Yonghong Fan

（School of Math.and Statistics Science，Ludong University，Shandong 264025，PR China）



THE SYMMETRIC POSITIVE SOLUTIONS OF 2n-ORDER BOUNDARY VALUE PROBLEMS ON TIME SCALES∗†

Yangyang Yu，Linlin Wang‡，Yonghong Fan

（School of Math.and Statistics Science，Ludong University，Shandong 264025，PR China）

Abstract

In this paper，we are concerned with the symmetric positive solutions of a 2n-order boundary value problems on time scales.By using induction principle，the symmetric form of the Green's function is established.In order to construct a necessary and sufficient condition for the existence result，the method of iterative technique will be used.As an application，an example is given to illustrate our main result.

Keywordssymmetric positive solutions；boundary value problems；induction principle；time scales；iterative technique

2000 Mathematics Subject Classification 34K10；34B27

1　Introduction

The theory of measure chains（time scales）was first introduced by Stefan Hilger in his Ph.D.thesis（see［1］）in 1988.Although it is a new research area of mathematics，it has already caused a lot of applications，e.g.，insect population models，neural networks，heat transfer and epidemic models（see［2，3］）.Some of these models can be found in［4-6］.Such as in［5］，Q.K.Song and Z.J.Zhao discussed the problem on the global exponential stability of complex-valued neural networks with both leakage delay and time-varying delays on time scales.By constructing appropriate Lyapunov-Krasovskii functionals and using matrix inequality technique，a delay-dependent condition assuring the global exponential stability for the considered neural networks was established.

In the past few years，more and more scholars concentrated on a positive solution of boundary value problems for differential equations on time scales（see［7-12］）.In［13，14］，by using some fixed point theorems，the existences of pseudo-symmetric solutions of dynamic equations on time scales were obtained.In［15，16］，the fourth order integral boundary value problems on time scales for an increasing homeomorphism and homomorphism were discussed.Recently，the conditions for the existence of symmetric positive solutions of boundary value problems were constructed in［17，18］. By applying an iterative technique，the existence and uniqueness of symmetric positive solutions of the 2n-order nonlinear singular boundary value problems of differential equation

were obtained.

In this paper，we are concerned with the existence of symmetric positive solutions of the following 2n-order boundary value problems（BVP）on time scales

where f：［0，σ（1）］×［0，∞）→［0，∞）is continuous and f（t，u）may be singular at u=0，t=0（and/or t=σ（1））.If a function u：［0，σ（1）］→R is continuous and satisfies u（t）=u（σ（1）-t）for t∈［0，σ（1）］，then we say that u（t）is symmetric on［0，σ（1）］.By a symmetric positive solution of BVP（1），we mean a symmetric function u∈C2n［0，σ（1）］such that（-1）iuΔ2i（t）＞0 for t∈（0，σ（1））and i= 0，1，···，n-1，and u（t）satisfies BVP（1）.We assume that σ（1）and 0 are all right dense.Throughout this paper we let T be any time scale（nonempty closed subset of R）and［a，b］be a subset of T such that［a，b］=｛t∈T：a≤t≤b｝.T satisfies

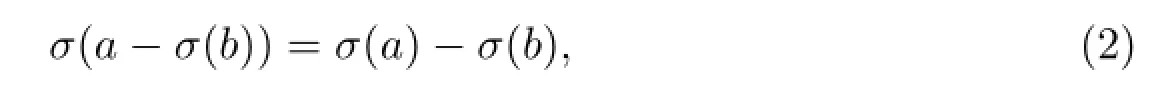
and it is easy to see that T=R or T=hZ satisfies（2）.And thuseT=｛σ（t）|t∈T｝= T.

2　Preliminary

Before discussing the problems of this paper，we introduce some basic materials for time scales which are useful in proving our main results.These preliminaries can be found in［17-20］.

Lemma 2.1［20］（Substitution）Assume that ν：T→R is strictly increasing andis a time scale.If f：T→ R is an rd-continuous function and ν is differentiable with rd-continuous derivative，then for a，b∈T，

Throughout this paper，similar to［18］，we assume that：

（A1）For（t，u）∈［0，σ（1）］×［0，∞），f（t，u）is symmetric in t，that is，f satisfies

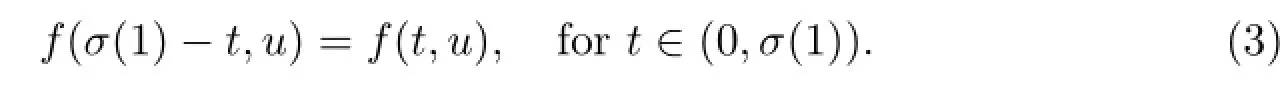
（A2）For（t，u）∈［0，σ（1）］×［0，∞），f is non-decreasing with respect to u and there exists a constant λ∈（0，1），such that if σ∈（0，1］，then

It is easy to see that（4）implies that if σ∈［1，∞），then

For convenience，in this paper we let

Lemma 2.2 Let v∈C［0，σ（1）］，then the following BVP

has a unique solution

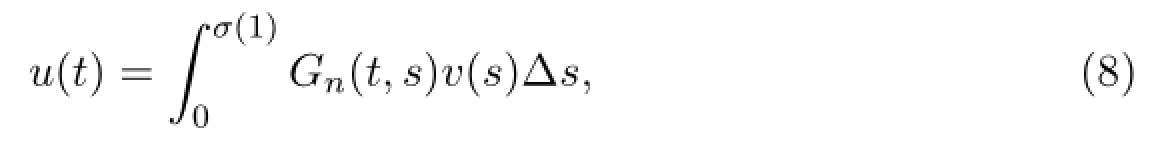
where Gn（t，s）is defined in［0，σ（1）］×［0，σ（1）］，and it follows from［19］that

which satisfies

It is easy to see

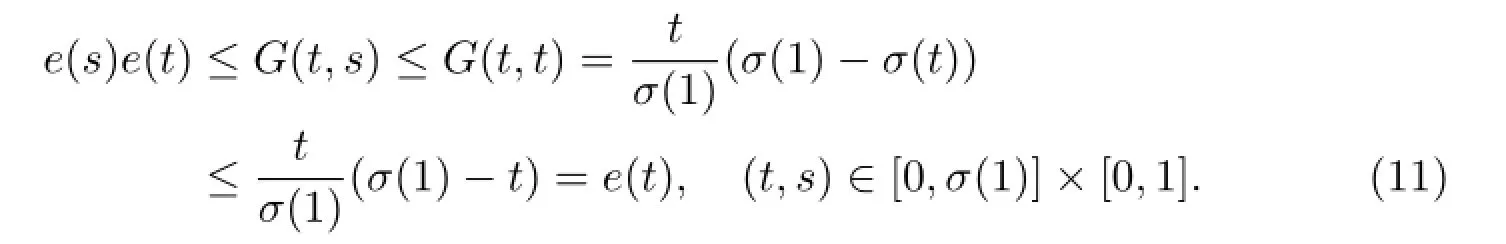
Lemma 2.3 For any t，s∈［0，σ（1）］，from（2）we have

Proof For any t，s∈［0，σ（1）］，when n=1，it is easy to see G1（σ（1）-t，σ（1）-σ（s））=G1（t，s）.

We consider Gn+1（σ（1）-t，σ（1）-σ（s））.

From（13），we obtain

Therefore，the proof of Lemma 2.3 is complete.

Remark 2.1 For any t，s∈［0，1］，we have

in a real space R，with the Green's function

Let E be the Banach space C（2n）［0，σ（1）］，and define

and there exist constants lu，Luwith 0＜lu＜1＜Lusuch that

图4右下表示LNAPI_SA对LNAPI_SA的脉冲响应结果，表明CPI给自身一个冲击，在第1期时便立即响应，产生正响应，且响应的效果逐渐增强，在第2期达到最大；之后响应的效果逐渐减弱，在第5期时变为0；之后继续下跌，产生负效应；在第7期时达到最大负效应；之后回升至第12期时再次变为0；之后趋于平稳。这说明CPI受自身影响大，尤其是在CPI上升后的3个月内影响最大，但在1年后产生了负影响。

Proof The proof is similar to that of Lemma 2.3 in［18］.

Lemma 2.5 If u（t）is a symmetric solution of BVP（1），then there exist constants c1，c2with 0＜c1＜1＜c2such that

ProofFor c1e（t）≤u（t），since u（t）is a symmetric positive solution of（1），we obtain u（t）＞0 and uΔΔ（（t））≤0 for t∈［0，σ（1）］.Choose a positive numberthen Lemma 2.4 implies c1e（t）≤u（t），t∈［0，σ（1）］.

and

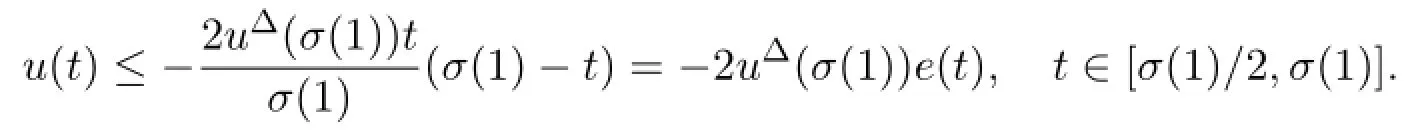
The symmetry of u（t）implies thatChoose a number c2＞Then

Clearly，（15）holds，and this completes the proof of Lemma 2.5.

Lemma 2.6［20］Let ［a，b］∈T，and f be right-dense continuous.If［a，b］consists of only isolated points，then

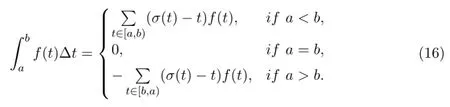
3　The Existence Result

Theorem 3.1Assume（A1）and（A2）hold.Then BVP（1）has at least one symmetric positive solution if and only if

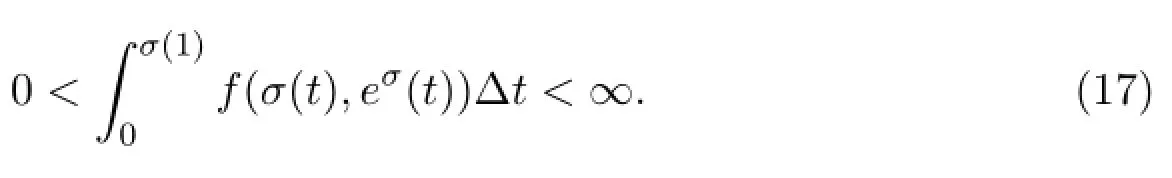
From（1），for t∈（0，σ（1）），when n is oddand when n is even，Then

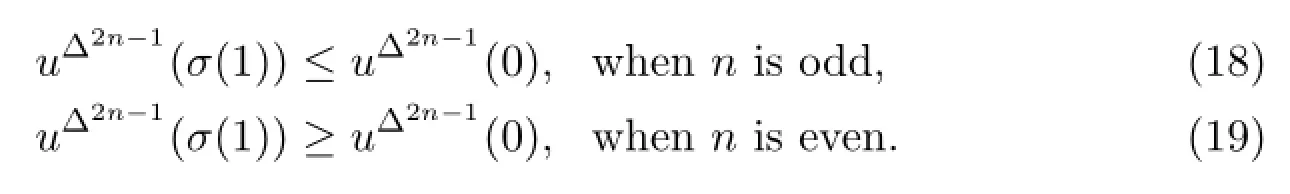
By（4），（5），（15），（18）and（19），

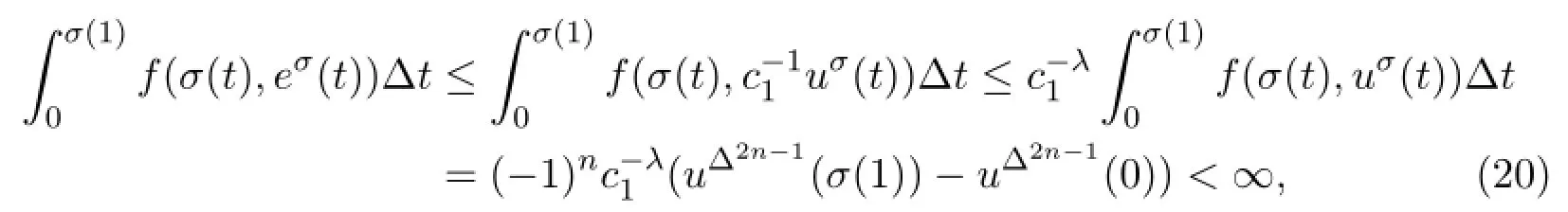
and

Now，（17）follows from（20）and（21）.Now assume that（17）holds.We will show that BVP（1）has at least one symmetric positive solution.

Define an operator T：E→E by

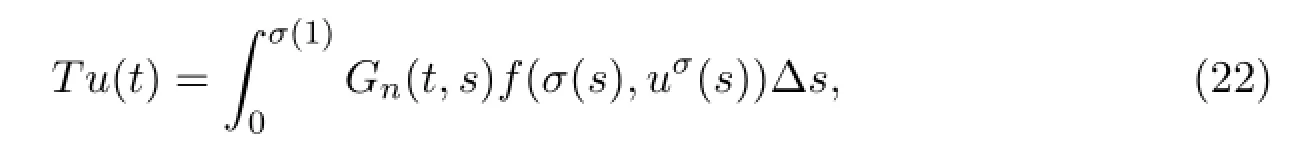
where Gn（t，s）is defined by（9）and（10）.It is clear that u is a solution if and only if u is a fixed point of T.

Claim 1 The operator T：P→P is completely continuous and non-decreasing.

In fact，for u∈P，it is obvious that Tu∈E，Tu（0）=Tu（σ（1））=0，Tu（t）＞0，for t∈（0，σ（1））.From（22），we have

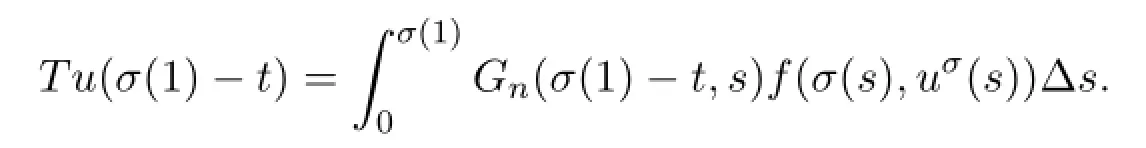
Thus，for any u∈P，from（4），（5），（10），（11）and（17），we obtain that for t∈［0，σ（1）］，

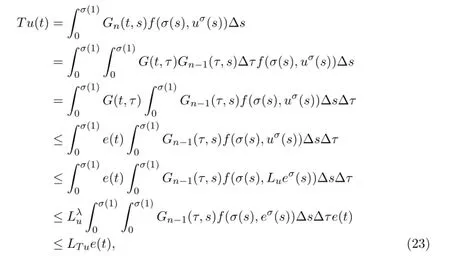
and

where LTuand lTuare positive constants satisfying

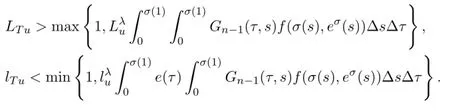
Thus，it follows from（23）and（24）that there exist constants LTuand lTuwith 0＜l＜1＜Lsuch that

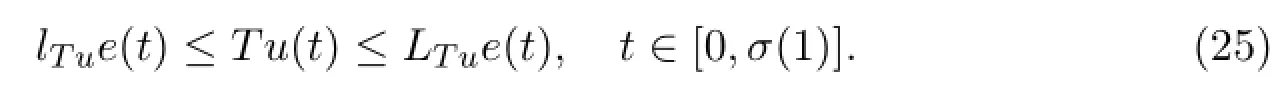
Therefore，Tu（t）∈P，that is，T：P→P.A standard argument can be used to show that T：P→P is completely continuous.

From（A2），it is easy to see that T is non-decreasing with respect to u.Hence，Claim 1 holds.

Claim 2 Let δ and γ be fixed numbers satisfying

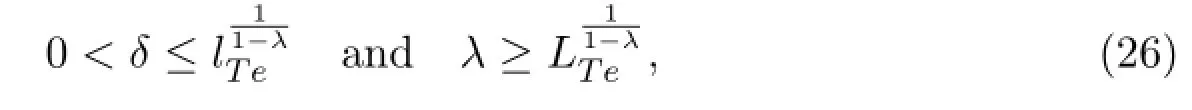
and assume

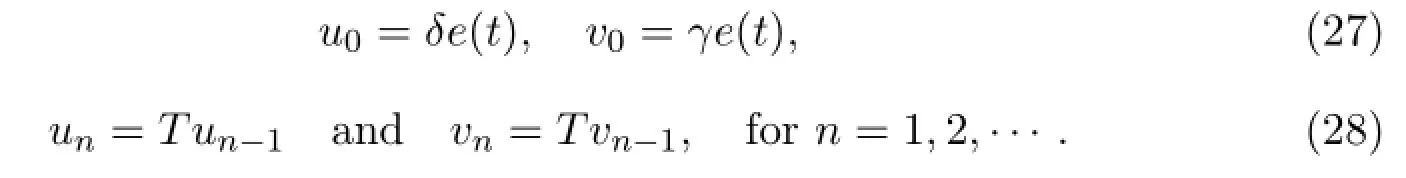
Then，

and there exists a u∗∈P such that

In fact，0＞lTe＜1＜LTesince Te∈P.So 0＜δ＜1＜γ.From（27），we have u0，v0∈P and u0≤v0.

On the other hand，

Since u0≤v0and T is nondecreasing，by induction，（27）holds.

that for any natural number n，

Thus，for each natural numbers n and p∗，we have

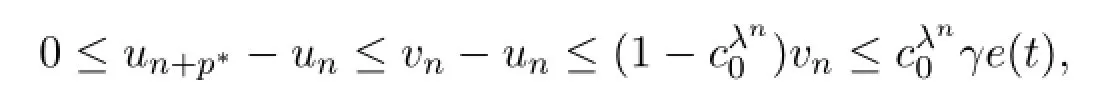
which implies that there exists a u∗∈P such that（30）holds，and Claim 2 holds.

Let n→∞in（28），we obtain u∗（t）=Tu∗（t），which is a symmetric positive solution of BVP（1）.Thus，the proof of Theorem 3.1 is complete.

4　Example

Example 4.1 Consider

where α∈R，0＜ β＜1.Let f（σ（t），uσ（t））= （σ（t））α（σ（1）-σ（t））αuβ（σ（t）），（t，u）∈［0，σ（1）］×［0，∞），then，for α＞-β-1，there is at least one symmetric positive solution of BVP（31）.

Note that the function f satisfies assumptions（A1）and（A2）.In fact，for（t，u）∈［0，σ（1）］×［0，∞），f（σ（1）-σ（t），uσ（t））=f（σ（t），uσ（t）），f is non-decreasing with respect to u and if σ∈（0，1］，there exists a constant λ with 0＜β≤λ＜1，such that f（σ（t），σuσ（t））≥σλf（σ（t），uσ（t））.

Thus，from Theorem 3.1，there is at least one symmetric positive solution of BVP（31）if and only if

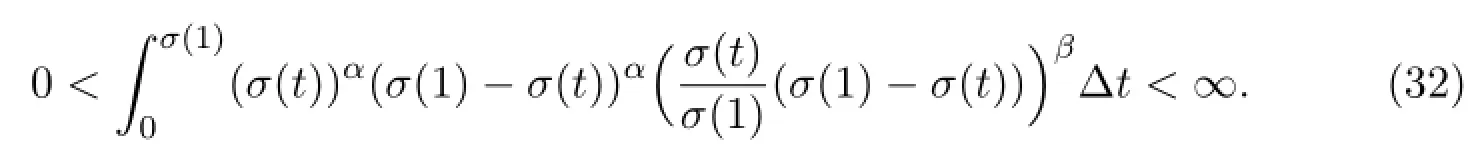
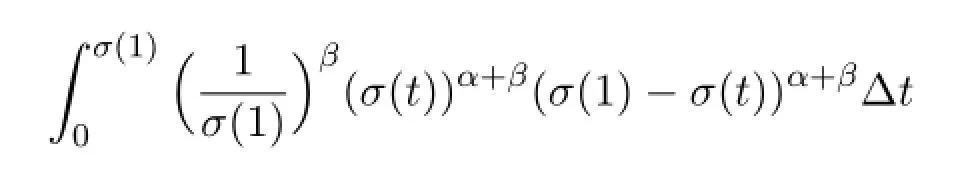
In fact，the integration converges if and only if α＞-β-1，then（32）holds.That is，for α＞-β-1，there is at least one symmetric positive solution of BVP（31）.

5　Discussion

Theorem 5.1Assume that（A1）and（A2）hold.Then BVP（1）has at least one symmetric positive solution if and only if

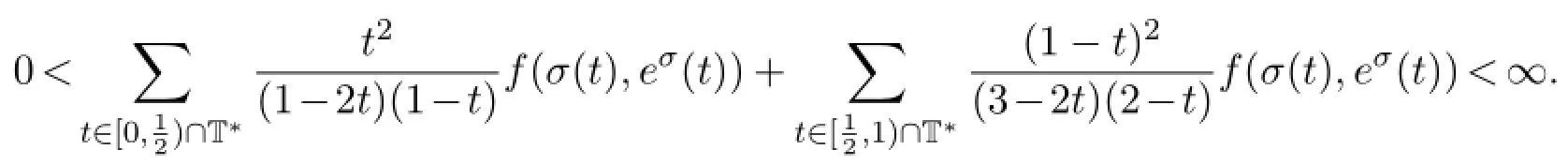
In particular，letting

it is easy to see that f satisfies assumptions（A1）and（A2），and there is

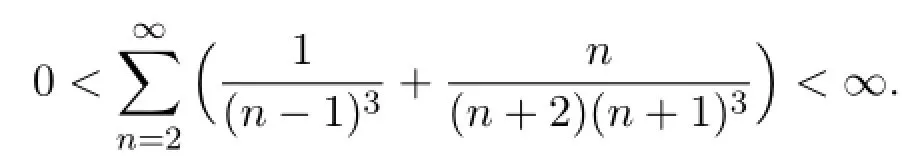
Thus，from Theorem 5.1，BVP（1）has at least one symmetric positive solution.

References

［1］S.Hilger，Ein Mabkettenkalk¨ul mit Anwendung auf Zentrumsmannigfaltigkeiten，Ph.D. thesis，Universit¨at of W¨urzburg，1988.

［2］R.P.Agarwal，M.Bohner，W.T.Li，Nonoscillation and Oscillation Theory for Functional Differential Equations，Pure Appl.Math.，Dekker，Florida，2004.

［3］B.Kaymak¸calan，V.Lakshmikantham，S.Sivasundaram，Dynamic Systems on Measure Chains，Kluwer Academic Publishers，Boston，1996.

［4］Q.Z.Xiao，B.X.Dai，Dynamics of an impulsive predator-prey logistic population model with state-dependent，Applied Mathematics and Computation，259（2015），220-230.

［5］Q.K.Song，Z.J.Zhao，Stability criterion of complex-valued neural networks with both leakage delay and time-varying delays on time scales，Neurocomputing，171（2016），179-184.

［6］L.L.Qian，E.Winfree，J.Bruck，Neural network computation with DNA strand displacement cascades，Nature，475（2011），368-372.

［7］H.R.Sun，L.T.Tang，Y.H.Wang，Eigenvalue problem for p-Laplacian three-point boundary value problems on time scales，J.Math.Anal.Appl.，331（2007），248-262.

［8］E.Cetin，S.Gulsan Topal，Higher order boundary value problems on time scales，J. Math.Anal.Appl.，334（2007），876-888.

［9］H.R.Sun，W.T.Li，Positive solutions for nonlinear three-point boundary value problems on time scales，J.Math.Anal.Appl.，299（2004），508-524.

［10］Y.B.Sang，H.Su，Several existence theorems of nonlinear m-point boundary value problem for p-Laplacian dynamic equations on time scales，J.Math.Anal.Appl.，340（2008），1012-1026.

［11］H.R.Sun，W.T.Li，Existence theory for positive solutions to one-dimensional p-Laplacian boundary value problems on time scales，J.Differential Equations，240（2007），217-248.

［12］L.Erbe，R.Mathsen，A.Peterson，Existence，multiplicity，and nonexistence of positive solutions to a differential equation on a measure chain，J.Comput.Appl.Math.，113：1-2（2000），365-380.

［13］Y.H.Su，Multiple positive pseudo-symmetric solutions of p-Laplacian dynamic equations on time scales，Math.Comput.Modelling，49（2009），1664-1681.

［14］Y.H.Su，W.T.Li，H.R.Sun，Triple positive pseudo-symmetric solutions of threepoint BVPs for p-Laplacian dynamic equations on time scales，Nonlinear Anal.，68（2008），1442-1452.

［15］N.A.Hama，F.Yoruk，Symmetric positive solutions of fourth order integral BVP for an increasing homeomorphism and homomorphism with sign-changing nonlinearity on time scales，Comput.Math.Appl.，59（2010），3603-3611.

［16］E.C¸etin，F.Serap Topal，Symmetric positive solutions of fourth order boundary value problems for an increasing homeomorphism and homomorphism on time-scales，Comput.Math.Appl.，63（2012），669-678.

［17］X.L.Lin，Z.Q.Zhao，Existence and uniqueness of symmetric positive solutions of 2norder nonlinear singular boundary value problems，Appl.Math.Lett.，26（2013），629-698.

［18］Y.Luo，Z.G.Luo，A necessary and sufficient condition for the existence of symmetric positive solutions of higher-order boundary value problems，Appl.Math.Lett.，25（2012），862-868.

［19］L.J.Kong，Q.K.Kong，Even order nonlinear eigenvalue problems on a measure chain，Nonlinear Anal.，52（2003），1891-1909.

［20］M.Bohner and A.Peterson，Dynamic Equations on Time Scales：An Introduction with Applications，Birkh¨auser，Boston，2001.

（edited by Liangwei Huang）

∗Supported by NNSF of China（11201213，11371183），NSF of Shandong Province（ZR2010AM022，ZR2013AM004），the Project of Shandong Provincial Higher Educational Science and Technology（J15LI07），the Project of Ludong University High-Quality Curriculum（20130345）and the Teaching Reform Project of Ludong University in 2014（20140405）.

†Manuscript received December 4，2015

‡Corresponding author.E-mail：wangll 1994@sina.com