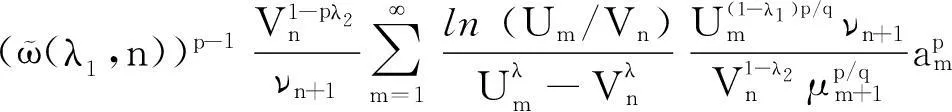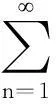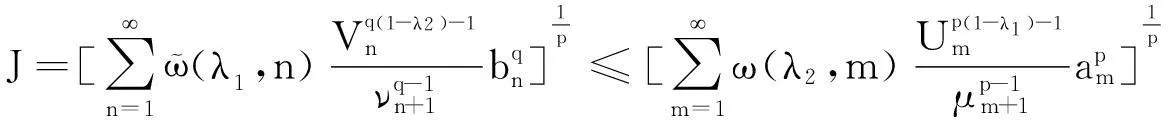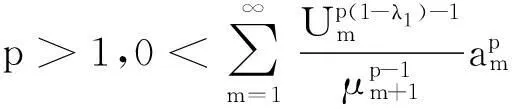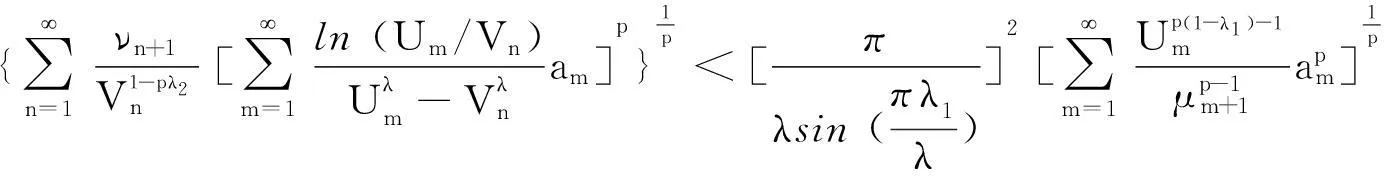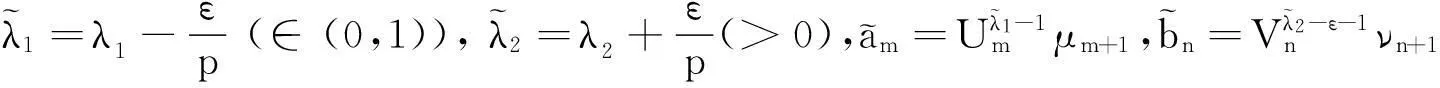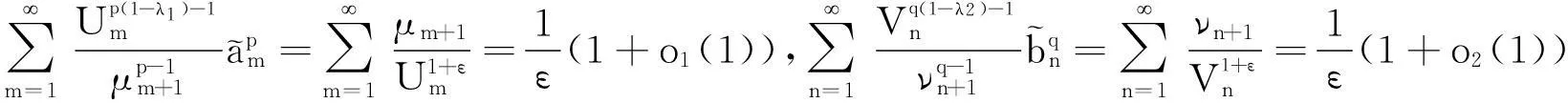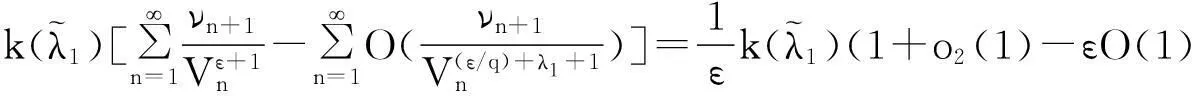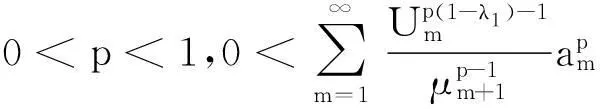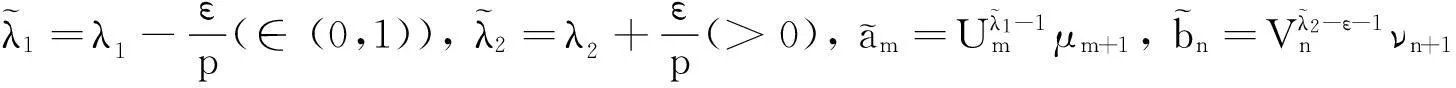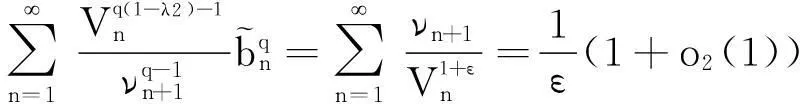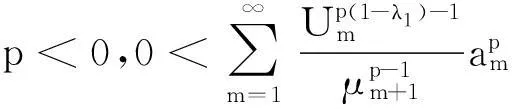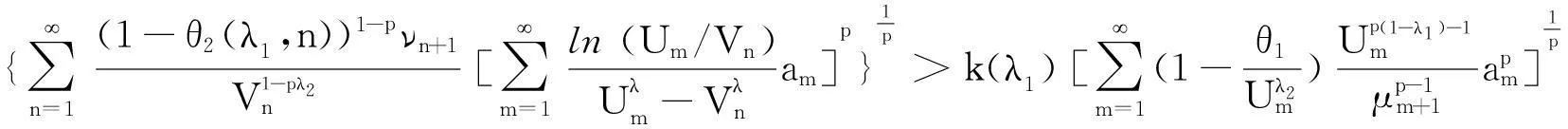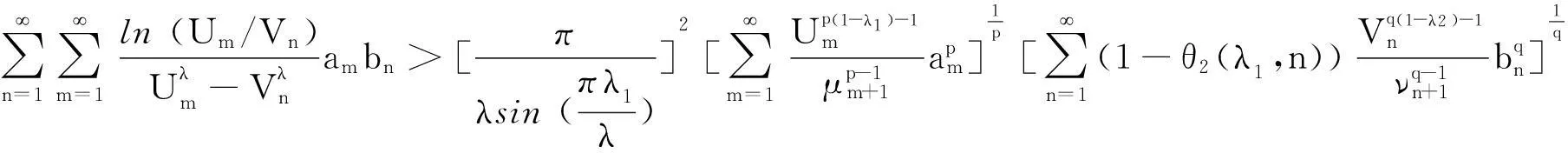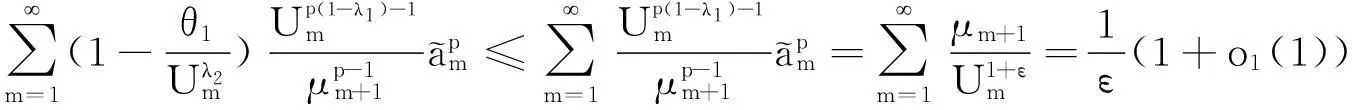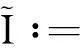杨必成

(广东第二师范学院 数学系, 广东 广州 510303)



关于一个加强的Hardy-Hilbert型不等式及其逆式

杨必成

(广东第二师范学院 数学系, 广东 广州 510303)

摘要:引入独立参数, 应用权系数的方法及Hermite-Hadamard不等式, 建立一个加强的具有最佳常数因子的Hardy-Hilbert型不等式,还考虑了其等价式与逆式.

关键词:Hardy-Hilbert型不等式;参数;权系数;等价式;Hadamard不等式

0引言

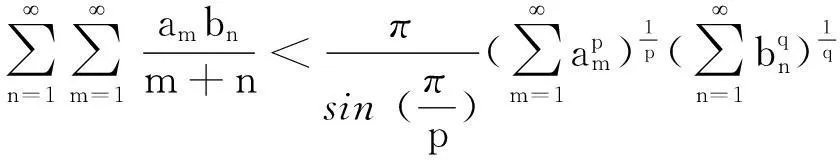
(1)

不等式(1)在分析学中有重要的应用(参阅文[2-5]).

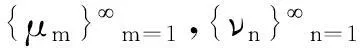
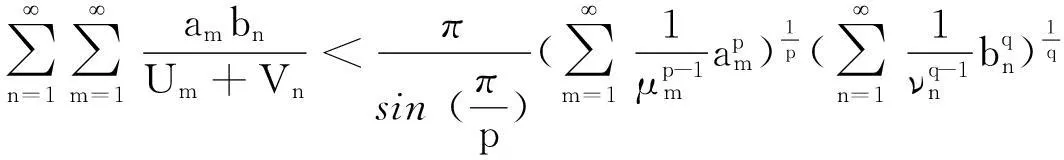
(2)

当μi=νi=1(i=1,2,…)时,式(2)变为式(1) .

2015年,文[6]引入参数α,λ>0,推广式(2)为:

(3)

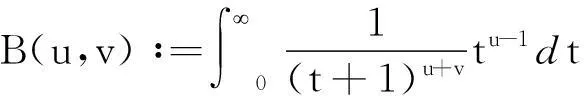
(4)

本文引入独立参数,应用权系数的方法及Hermite-Hadamard不等式,在式(3)的类似条件下,建立如下一个具有最佳常数因子的Hardy-Hilbert型不等式:

(5)

本文的主要目的是考虑式(5)的加强式、等价式及逆式.

1引理及例

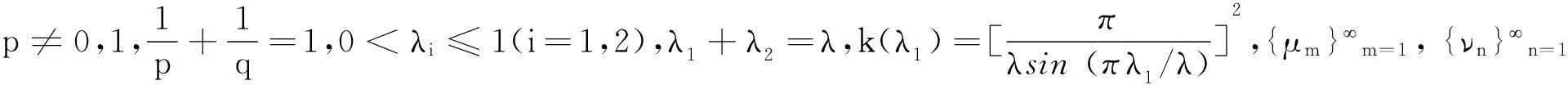
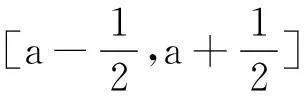
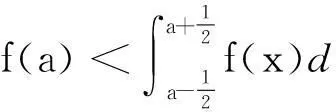
(6)

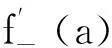
例1设μ(t)∶=μm,t∈(m-1,m](m=1,2,…);v(t)∶=νn,t∈(n-1,n](n=1,2,…),

(7)

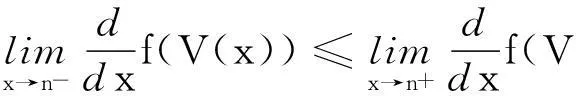
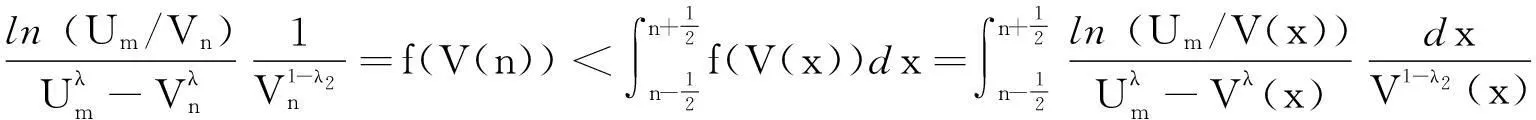
(8)

引理2定义如下权系数：

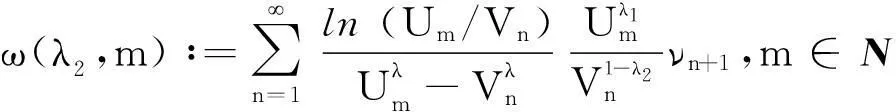
(9)

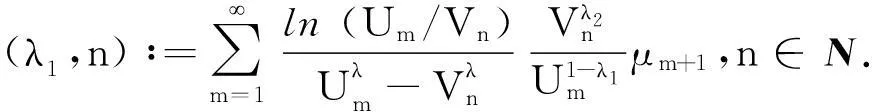
(10)

则有如下不等式:

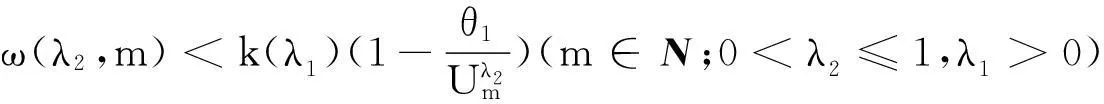
(11)

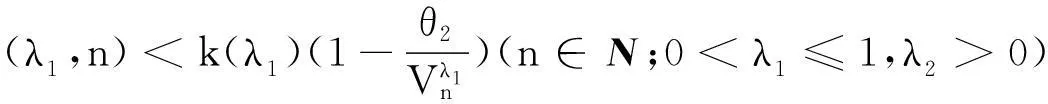
(12)

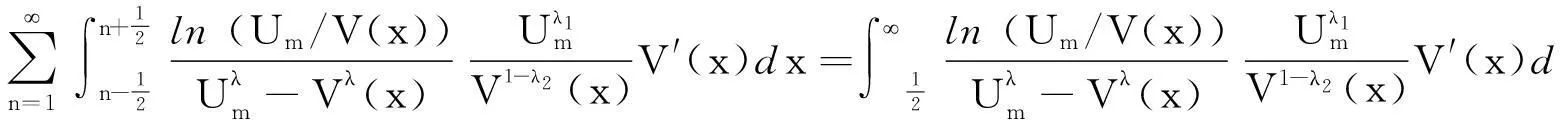
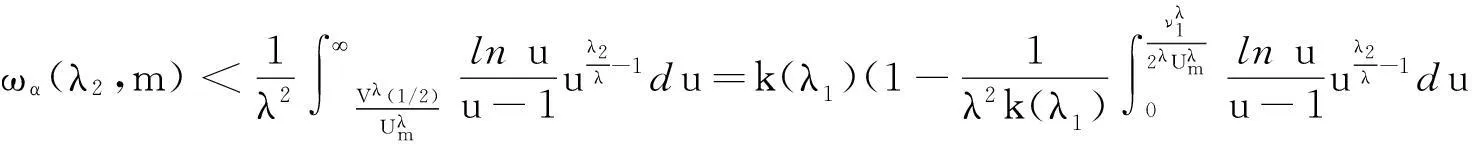
(13)

由式(13),可得式(11)成立.同理,由对称性,可证式(12)成立.证毕.

引理3我们还有如下权系数的不等式:

k(λ1)(1-θ1(λ2,m))<ω(λ2,m)(m∈N;0<λ2≤1,λ1>0),

(14)

k(λ1)(1-θ2(λ1,n))<ϖ(λ1,n)(n∈N;0<λ1≤1,λ2>0),

(15)

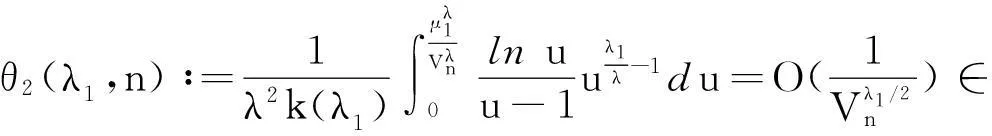
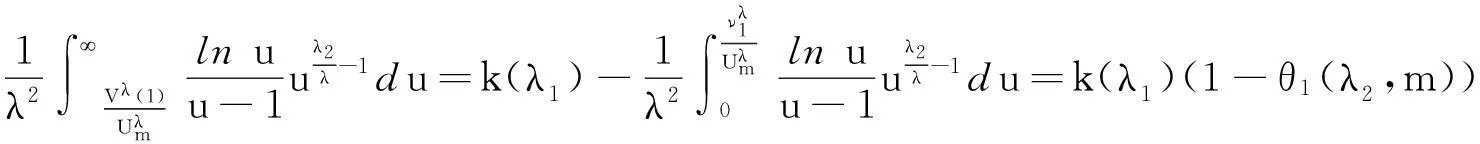
(16)

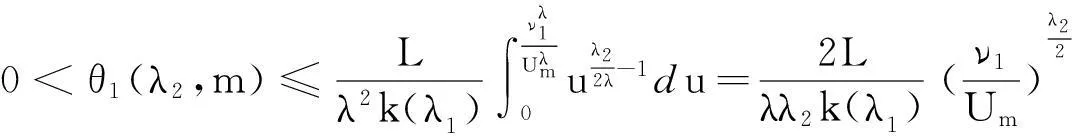
故式(14)成立. 同理,由对称性,知式(15)亦成立. 证毕.

引理4任ε>0,有

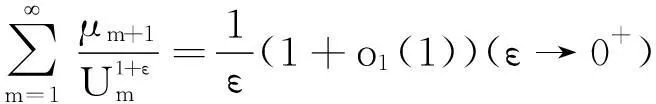
(17)

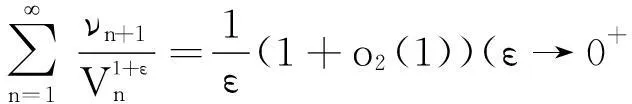
(18)

证明由递减性质,我们有

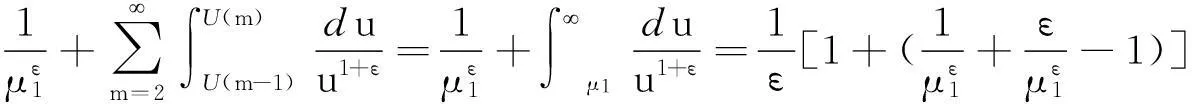
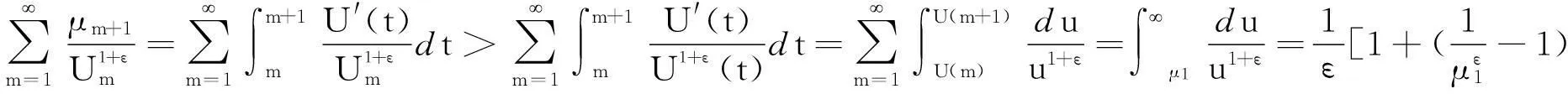
故式(17)成立.同理,式(18)亦成立. 证毕.

引理5若p>1,则有如下等价不等式:

(20)

若0

证明配方,并由带权的Hölder不等式[8]及式(10),式(9),有

(21)

(22)

(23)

(24)

故式(20)成立,且它与式(19)等价.

若0

2主要结果

(25)

(26)

这里,常数因子k(λ1)都为最佳值,θi(i=1,2)依引理2所示.

特别地,式(25),式(26)可导出具有最佳常数因子的式(5)及如下等价式:

(27)

证明在式(20),式(21)中应用式(11),式(12),可得式(25)与(26)成立且等价.

若有正常数K≤k(λ1),使取代式(5)的常数因子k(λ1)后仍成立,则特别有

(28)

式(27)的常数因子必为最佳值.不然,由式(23)(置ϖα(λ1,n)=1),必导出式(5)的常数因子也不为最佳值的矛盾.易由反证法证得式(25)及式(26)的常数因子也为最佳值.证毕.

(29)

(30)

这里,常数因子k(λ1)都为最佳值,θi(i=1,2)依引理2所示.

特别地,式(29),式(30)可导出如下具有最佳常数因子的等价式:

(31)

(32)

若有正常数K≥k(λ1),使取代式(31)的常数因子k(λ1)后仍成立,则特别有

即有k(λ1)≥K(ε→0+). 故K=k(λ1)为式(31)的最佳值. 证毕.

(33)

(34)

这里,常数因子k(λ1)都为最佳值,θi(i=1,2)依引理2所示.

特别地,式(33),式(34)可导出如下具有最佳常数因子的等价式:

(35)

(36)

若有正常数K≥k(λ1),使取代式(35)的常数因子k(λ1)后仍成立,则特别有

即有k(λ1)≥K(ε→0+). 故K=k(λ1)为式(33)的最佳值. 证毕.

参考文献：

[1]HARDYGH.NoteonatheoremofHilbertconcerningseriesofpositiveterms[J].ProceedingsLondonMathSoc, 1925, 23(2):RecordsofProcxlv-xlvi.

[2]HARDYGH,LITTLEWOODJE,POLYAG.Inequalities[M].Cambridge:CambridgeUniv.Press, 1952.

[3]MITRINOVIODS,PECARICJE,FINKAM,Inequalitiesinvolvingfunctionsandtheirintegralsandderivatives[M].Boston:KluwerAcaremicPublishers, 1991.

[4] 杨必成.算子范数与Hilbert型不等式[M].北京:科学出版社,2009.

[5]YANGBi-cheng.DiscreteHilbert-typeinequalities[M].Sharjah,TheUnitedArabEmirates:BenthamSciencePublishersLtd,2011.

[6] 杨必成. 一个推广的Hardy-Hilbert型不等式[J].广东第二师范学院学报,2015, 35(3): 1-7.

[7] 王竹溪,郭敦仁.特殊函数论[M].北京:科学出版社,1979.

[8] 匡继昌.常用不等式[M].济南:山东科技出版社,2004.

收稿日期：2015-12-03

基金项目：国家自然科学基金资助项目(61370186)

作者简介：杨必成,男,广东汕尾人,广东第二师范学院数学系教授.

中图分类号：O 178

文献标识码：A

文章编号：2095-3798(2016)03-0001-07

On a Strengthened Version of a Hardy-Hilbert-Type Inequality and the Reverses

YANG Bi-cheng

(Department of Mathematics, Guangdong University of Education,Guangzhou, Guangdong, 510303, P. R. China)

Abstract:By introducing independent parameters, and applying the way of weight coefficients and Hermite-Hadamard’s inequality, a strengthened version of a Hardy-Hilbert-type inequality with a best possible constant factor is proved. Furthermore, the equivalent form and the reverses are considered.

Key words:Hardy-Hilbert-type inequality; parameter; weight coefficient; equivalent form; Hermite-Hadamard’s inequality