秦泗吉　邓　超　杨　莉　孔晓华　王耀华



圆锥形件拉深成形应力应变的直接积分解法

秦泗吉邓超杨莉孔晓华王耀华

燕山大学,秦皇岛,066004

摘要：针对圆锥形件的拉深成形，在平面应力和比例加载条件下，采用参数方程的方法分析得到了变形区应变的微分方程。可在圆锥形件的凸缘区、凹模圆角区及锥壁区分别根据应变微分方程，代入相应的边界条件，采用直接积分得到应力、应变解，将应用于轴对称平面内的积分解法推广至分析圆锥形件的拉深成形问题。在凸缘区，锥角等于0；在锥壁区，锥角等于一定值；在凹模圆角区，将圆角部分的弧段分成若干个微锥段，每一微锥段都可分别作为一个小的等锥角的锥环处理。采用该方法，不仅可以计算锥形件的拉深成形问题，而且可以计算曲面形状已知的一般轴对称曲面零件的成形问题。用直接积分法替代迭代法求解非线性方程，使求解过程大大简化。选取厚0.87mm的ST16板材进行了拉深成形实验，以板坯内层为测量面，测量了凸缘区、凹模圆角区和锥壁区的应变分布，理论计算结果与实验结果一致。

关键词：板材成形；圆锥形零件拉深；平面应力模型；直接积分解法

0引言

在板材冲压成形中,圆锥形件是典型的曲面类零件,在成形过程中既有径(经)向受拉、周向受压的拉深成形区域，一般又存在双向拉应力的胀形区域，在凹模圆角和凸模圆角区域还会产生弯曲变形。变形过程中，可能出现的两种失稳形式是破裂和起皱，其中,起皱失稳可能出现在凸缘区和悬空的锥壁区。圆筒形件可以认为是当圆锥形件的大端尺寸接近小端尺寸时的特例，而其他轴对称曲面类零件又可以看作由一系列的微锥组成。此外，圆锥形零件在板材冲压成形中也有广泛应用，如汽车灯罩、消音器后盖及轮毂防尘罩、电振动喇叭筒和圆锥滚子轴承保持架等都是圆锥形零件[1]。因此,对圆锥形件成形的研究是有理论意义和实际意义的。

许多学者对包括圆锥形件的轴对称成形问题进行了研究，涉及拉深[2-4]、胀形[5]和内孔翻边[6]等问题。在分析轴对称成形问题时，主要采用两种假设模型[2]:一是板坯厚度不变的平面应变假设，二是板平面(或曲面)法线方向应力为零的平面应力假设。当假设板坯厚度不变时，可使分析过程大大简化,所以许多学者常用这种假设模型[2-4,7-9]。

由于板材成形在很多情况下,垂直于板平面或曲面方向上无力的作用或作用力很小(即使采用液压成形方式,板坯法线方向的应力也很小[10]),此时板材成形过程更接近平面应力状态,因此,按平面应力模型进行分析更接近实际情况。

关于平面内的轴对称成形问题，在平面应力和比例加载等假设条件下,李敏华[11]给出了参数方程的直接积分求解方法,改进了Nadai[12]、Millenson等[13]给出的需要不断迭代才能得到解析解的方法，显著简化了求解过程。文献[8,14]将轴对称问题的参数方程分析方法用于求解轴对称成形板平面内冲压成形问题,给出了不考虑厚度变化时用参数方程形式表示的凸缘区应力显式表达式。但由于轴对称成形问题多数情况下都涉及凸缘区以外的成形区域，这些区域的形状是锥面或曲面，无法采用平面应力假设条件下的直接积分解法。这也是该方法没有得到推广应用的原因之一。

本文将求解平面内轴对称问题的分析方法推广至求解圆锥形件的成形问题，给出了基于参数方程的积分解法。针对圆锥形零件的拉深成形，将变形区主要划分为凸缘区、凹模圆角区、悬空锥壁区和凸模圆角区。对前三个区域都给出了基于积分解法的应力、应变解，采用厚0.87mm的ST16板材进行了圆锥形件拉深实验，测量了应变分布，理论计算值与实验结果一致。采用本文方法,还可将积分解法推广至求解一般轴对称成形问题。

1变形协调方程及平衡方程

1.1变形协调方程

如图1所示，从圆盘或圆环的平板毛坯变形为圆锥形壳体，变形后某一微锥形环内外半径分别为r和r+dr,若对应半径是r的质点变形后的径向位移为u,则变形前微圆环的内外缘半径分别为r-u和r-u+dr-du。

α为锥面母线与竖直方向的夹角，又称为半锥角。由应变的定义，可以得到经向应变ερ和周向应变εθ[11]:

(1)

(2)

消去u,可得

(3)

对于平面内的轴对称成形，可令α=π/2。

1.2微分平衡方程

在圆锥形件的成形中，每一变形质点的主轴方向为经向、纬向及法向，对应的三个方向的应力分别表示为σρ、σθ和σz。截取一微锥壳环,然后用过轴对称线的平面将其剖开,得到一半微锥环,其受力情况如图2所示。

图2中符号含义如下:OO′为对称轴线；r、α的含义与图1相同;σρ、σρ+dσρ分别为上下纬端面上作用的经向应力;σθ为作用于微锥壳体上的纬向应力;t、t+dt分别为上下纬端面处的厚度;ds为微锥壳体的母线长度;p为作用于壳体下表面的单位压力。

分别在轴线方向和水平方向列平衡方程，有

cosαd(σρtr)=prsinαds

(4)

σθtds-sinαd(σρtr)=prcosαds

(5)

由式(4)、式(5)，并注意到ds=dr/sinα,得

d(σρtr)=σθtdr

(6)

式(6)与轴对称平面内成形的微分方程在形式上完全相同，也可表示成

(7)

2参数方程及边界条件

对于圆锥形件成形的锥壁区,忽略板厚方向的应力,根据等效应力的定义,有

(8)

式中,σ为等效应力;R为板厚方向性系数。

参照平面内的轴对称成形问题的解法[11],应力可以用参数方程的形式表示:

(9)

式中,ω为参数。

比例加载条件下,等效应变ε的参数表达式为

(10)

由应力参数方程式(9)，得

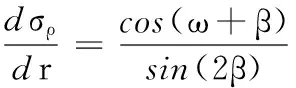
(11)

将式(9)、式(11)代入式(7),并利用体积不变条件dt/t=-dερ-dεθ,得

(12)

设材料的等效应力应变关系满足σ=Bεn(B为强度系数,n为硬化指数),则

(13)

将式(13)代入式(12),得

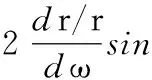
(14)

由参数方程式(10),得

(15)

将式(10)、式(15)代入式(3)，得

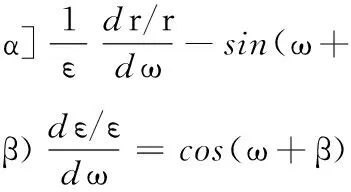
(16)

在微分方程(式(14)和式(16))中,变量ε、r是参变量ω的函数，当边界条件已知时,方程的解是确定的。

图3所示为圆锥形件拉深至某一位置时的各变形区,AB为凸缘区,BC为凹模圆角区,CD为锥壁区,DE为凸模圆角区,EF为锥底。

当拉深位置一定时,若采用直母线假设,则DC为直线,锥形件的锥角α已知。设α=α0,α0可由拉深位置、模具几何尺寸以及板厚变化情况确定。

板材平面内轴对称问题可认为是圆锥形件成形的一个特例，因式(14)不含变量α,对凸缘区的变形,在求解时令α=π/2,代入式(16)即可。

圆锥形件拉深时,因凹模圆角对板坯的法向作用力很小，凹模圆角区板坯的变形可以近似认为只有经向和纬向应力。如图3所示，设凹模圆角处的板坯形状与凹模圆角轮廓形状一致，在凹模圆角处,BC与AB、CD分别在B、C点相切。将圆弧BC分成若干个弧段，当弧段尺寸较小时，该弧段接近直线段，其对应的变形区可作为一个小锥环处理。设小弧段的长度为ΔS，该处切线与竖直方向夹角为αi，令α=αi，应变微分方程和求解过程与锥壁区相同。

对于圆锥形件的拉深成形问题，采用积分解法的计算次序是凸缘区、凹模圆角区和悬空侧壁区。在凸缘变形区,设F为压边力,μ为摩擦因数,tw为凸缘外缘对应的板坯厚度,ω0为参数初始值,ε0为应变初始值。则边界条件如下：当ρ=Rw(Rw为凸缘外缘半径)时

σρ=F/(Rwtw)

ω0=2π-arccosm-β

ε0=ln(R0/Rw)

当不考虑摩擦时,σe初值为0,ω0=3π/2-β。

在凹模圆角区和悬空侧壁区，只要给出初始点的应变作为边界条件，由式(14)和式(16)，应变与坐标位置的关系是确定的。凸缘区与凹模圆弧交接的位置对应的应变可作为凹模圆角区的初始值,凹模圆角区与悬空侧壁区交接位置对应的应变可作为悬空侧壁区的初值。

3直接积分解法

将式(14)、式(16)联立,消去dr/r,设方程为

(17)

b=2cos(ω+β)sinβcosω-cos(ω+β)n/ε

c=2εcos(ω+β)sinβsinω-sin(ω+β)

d=1-exp(2εcosβsinω)/sinα

e=-sin(ω+β)f=εcos(ω+β)

对于给定的边界条件,一般需要采用迭代解法才能得到微分方程式(17)的解。

对于等锥角的圆锥形件成形问题,已知边界条件,即当ω=ω0时,ε=ε0,采用直接积分解法求任意ω对应的应变ε的计算过程和收敛性可说明如下:

(1)将区间(ω0,ω)N等分,各值为ωi(i=0,1,…,N),对应的应变值为εi(i=0,1,…,N),每一区间的增量Δω=(ω-ω0)/N。

(2)根据微分学的知识，有

(18)

式中,o(Δω)为比Δω高级的微分项。

因此,当参变量由ω0增加为ω1时,对应的应变ε1可以近似表示为

(19)

(3)一般地,当已知ωi-1(i≥1)对应的应变为εi-1时,其临近点ωi对应的应变εi近似表示为

(20)

(4)对于任意ω,对应的应变值近似为

(21)

在步骤(2)～(4)中,当ω和ε已知时,由式(17)可得到该点的一阶导数。因此,式(21)又可写为

(22)

根据积分的定义，有

(23)

N值越大,计算精度越高。步骤(1)～(4)的求解过程实际上是用数值方法计算积分问题,即

(24)

在计算过程中,每次求出ε后,代入式(14)或式(16)可求出dr/r,积分后可得到r。这样就可得到等效应变ε与位置r之间的关系，进而可求出应力、应变。

4圆锥形件拉深成形应力应变分布

4.1圆角区和锥壁区α值的确定

4.1.1凹模圆角区α值的确定

拉深过程中,板坯经过凹模圆角时的变形非常复杂,为了简单起见,设板坯经过凹模圆角时,板坯内层保持凹模圆角的外轮廓形状。如图4所示，根据几何关系可建立质点位置半径r和α的关系:

(25)

4.1.2锥壁区α值的确定

分析表明,悬空侧壁区锥角对应变分布的影响很大。如图3所示,设从凸缘区边缘A至凸模圆角与锥底连接点E为变形区。

在计算出凸缘区、凹模圆角区的应变分布之后,可按体积不变条件确定锥角。实际计算时，暂以变形前后总面积不变，初步确定锥角α0,再根据计算后的厚度变化按体积不变进行修正。计算表明,采用面积不变假设与体积不变假设结果相差不大,一般需修正2～3次就能使体积计算值收敛。

采用积分法求解，实际是将板坯分成若干微段，成形后的体积很容易得到,体积可按下式进行计算:

(26)

式中,Vi为各部分的体积;rai、rbi分别为各计算区间的起止点对应的径向坐标;ri、ti分别为位置半径和相应位置的板坯厚度;αi为对应计算段的板坯所在弧或平面与轴对称线夹角。

4.2应力、应变分布

取凹模内半径Rd=26.82 mm，凸模外半径Rp=20 mm，凹模圆角rd=13 mm,凸模圆角rp=5 mm，原始毛坯半径R0=55 mm,板厚0.87 mm。压边力取5 kN，板坯与凹模、板坯与压边圈之间的摩擦因数都取0.06,不考虑板坯在凹模圆角处的摩擦。材料选用ST16板材，性能参数经拉伸实验确定:B=511.4 MPa,n=0.26,R=2.243。拉深相对位置Rw/R0分别为0.919、0.878和0.838，采用上述计算方法得到的应变分布和应力分布分别如图5～图10所示。

由前面的理论分析可知，应力值与材料强度系数B成比例关系，为了简明起见，图8～图10采用了应力与强度系数的比值。

图5～图7显示,经向应变为正值,除接近凸模圆角附近的很小区域外，其他区域的纬/周向应变都为负值。从凸缘外缘到凸模圆角，板坯厚度应变由正变为负。随着拉深过程的进行,变形程度逐渐增大,经向应变、周向应变绝对值最大值也逐渐增大。

图8～图10表明,经向应力都为拉应力，周向应力分为拉和压两个区域。经向应力最大值随拉深变形程度的增大而逐渐增大。周向应力在大部分区域都为负值(压应力)，但在接近凸模圆角的区域为正值(拉应力)，且随着变形程度的增大，拉应力值也增大。接近凸缘区变形性质为经向受拉、周向受压的拉深，接近凸模圆角区变形为双向受拉的胀形，且随着变形程度的增大，双向应力越来越接近。

5圆锥形件拉深成形实验

圆锥形件拉深成形实验选取ST16板坯,板坯几何尺寸、性能参数、拉深工艺参数和模具几何参数与前面理论计算相同。实验过程中先在圆形毛坯上印制网格，再进行拉深成形实验，测量成形后板坯的应变分布。

拉深成形时，将板坯印制有网格的面放置到凹模一侧，变形后这个表面即为图4所示的内层，其与模具轮廓形状最接近。为了减小摩擦的影响，选择了薄膜润滑。如图11所示，三个试件拉深高度H从左至右依次为22.87 mm、27.26 mm和32.53 mm,对应的法兰外缘相对半径Rw/R0分别为0.919、0.878和0.838。

成形后的试件用自动应变测量系统VialuxAutoGrid进行测量。为了真实地反映应变的分布情况，将拉深试件的整个凸缘区、凹模圆角区和悬空侧壁区所有网格节点都作为测量点,将经向应变、周向应变测量值与相应各点所在位置半径之间的关系表示在图12～图14上。图中光滑曲线为理论值，离散点为实验值。实验得到的经向应变、周向应变应变值都分别集中在一个条带区域内。

实验和计算结果表明,采用直接积分法得到的理论计算值与实测的周向应变值一致,经向应变值的理论计算结果与实测值在凹模圆角区、接近凹模圆角的凸缘,以及接近凸模圆角的悬空侧壁区相差稍大,但变化趋势基本一致。由于理论计算采用了薄膜理论的平衡方程式，没有考虑弯曲的影响，另外采用直母线假设等，这些都可能造成了理论计算与实际存在一定的偏差。板坯在凹模圆角的弯曲变形主要是沿经向的,因而对周向应变影响不大。

6结论

(1)对圆锥形零件的成形问题，给出了基于参数解法的直接积分解法和具体求解过程，这一方法避免了进行复杂的迭代求解。

(2)选取0.87mm厚的ST16板材和一定的模具尺寸及工艺条件,对圆锥形件拉深成形，求解得到了板坯拉深至不同位置时的应力应变分布。

(3)进行了圆锥形件拉深成形实验，实验测量了凸缘区、凹模圆角区和悬空侧壁区的应变分布。结果表明，在相同变形条件下采用直接积分法计算的周向应变与实测结果较接近，而经向应变在某些区域差别稍大，但趋势基本一致。

参考文献:

[1]万敏.圆锥形零件冲压成形极限的研究[D].哈尔滨：哈尔滨工业大学, 1995.

[2]FazliA,ArezooB.PredictionofLimitingDrawingRatioConsideringtheEffectiveParametersofDieArcRegion[J].J.Mat.Proc.Technol.,2012,212(4):745-751.

[3]任运来，吕亚臣，彭加耕，等.相对厚度对锥形零件拉深成形的影响[J].机械工程学报，2010, 46(8):51-55.

RenYunlai,LüYachen,PengJiageng,etal.EffectofRelativeThicknessonTaperedPartDrawing[J].JournalofMechanicalEngineering, 2010, 46(8):51-55.

[4]秦泗吉. 轴对称拉深成形凸缘区应力应变解析求解[J]. 机械工程学报, 2011, 46(24):20-25.

QinSiji.AnalyticalSolutionofStressandStraininFlangeDeformationinAxisymmetricDeepDrawingProcess[J].JournalofMechanicalEngineering, 2011, 46(24):20-25.

[5]戴春俊.板材胀形过程应变分析的实验-数值混合法[D].哈尔滨：哈尔滨工业大学,2013.

[6]纪莲清，谢欢.内孔翻边时变形区应力应变规律研究[J]. 锻压技术,2007,32(1):20-24.JiLianqing,XieHuan.StressandStrainRuleStudiesofDeformactionAreaofInsideHoleFlange[J].Forging&StampingTechnology,2007,32(1):20-24.[7]赵军.圆锥形件拉深成形智能化的研究[D].哈尔滨：哈尔滨工业大学，1997.

[8]梁炳文,胡世光.板料成形塑性理论[M].北京:机械工业出版社,1987.

[9]ThiruvarudchelvanS,TanMJ.ANoteonFluid-pressure-assistedDeepDrawingProcesses[J].J.Mat.Proc.Technol., 2006,172(2):174-181.

[10]WuYS,WangXY,XiaJC.MultipointBlankHolderforceControlinHydroformingofFuelTank[J].ChineseJournalofMechanicalEngineering，2006，19(2)：200-204.

[11]李敏华.硬化材料的轴对称平面塑性平面应力问题的研究[M].北京:科学出版社,1960.

[12]NadaiA.PlasticBehaviorofMetalsintheStrainHardeningRange,PartI[J].J.Appl.Phys.,1937,8(3):205-213.

[13]MillensonMB,MansonSS.DeterminationofStressesinGas-turbineDisksSubjectedtoPlasticFlowandCreep[R].NewYork:NACA,1948.

[14]刘幺和,胡世光.板料的n、r值对应力应变分布的影响[J].锻压技术, 1982,7(3):11-18.

LiuYaohe,HuShiguang.TheeffectofnandronDistributionsofStressandStrain[J].Forging&StampingTechnology,1982,7(3):11-18.

(编辑陈勇)

ADirectIntegralMethodtoSolveStressandStrainofConicalPartsinDeepDrawingProcess

QinSijiDengChaoYangLiKongXiaohuaWangYaohua

YanshanUniversity,Qinhuangdao,Hebei,066004

Keywords：sheetmetalforming;conicalpartindeepdrawing;planestressmodel;directintegralmethod

Abstract:Undertheconditionsofplanestressandproportionalloading,differentialequationsofstrainandstressindeformationzoneofconicalpartindeepdrawingwereobtainedbythemethodofparametricequation.Aftersolvingthedifferentialequationsunderthecorrespondingboundaryconditionsintheregionsofflange,diecornerandconicalwalloftheconicalpartthestressesandstrainsmightbeobtainedrespectivelyineveryregionsbythedirectintegralmethod.Theapplicationsofthedirectintegralmethodwereextendedfromsolvingthein-planeaxisymmeticsheetmetalformingproblemstoanalyzeconicalpartdeepdrawingprocess.Theconicalangleswereequaltozeroandacertainvalueinflangeregionandconicalwallrespectively.Thediearcregionsmightbedividedintoseveralsmallsegmentsandeachofthemcouldbetakenasaconicalpartwithconstantconicalangle.Thismethodwasappliedtosolveconicalpartdeepdrawingproblemsandtoanalyzetheformingproblemofaxisymmetriccurvedpartswithgivenprofileshape.Asthesubstituteofiterationmethod,thedirectintegralmethodwasappliedtosolvenonlinearequationsandthesolvingprocesscouldbesimplifiedgreatly.Theexperimentsofconicalpartdeepdrawingwerecarriedoutbyusing0.87mm-thickST16sheetandthestraindistributionsinflange,diearcandconicalwallregionsweremeasured.Itshowsthattheanalyticalsolutionsbythedirectintegralmethodareaccordantwithexperimentalresults.

收稿日期：2015-04-09

基金项目：国家自然科学基金资助项目(51175451)

作者简介：秦泗吉,男,1963年生。燕山大学机械工程学院教授、博士研究生导师。主要研究方向为先进成形设备、板材成形新工艺等。邓超,男,1989年生。燕山大学机械工程学院硕士研究生。杨莉,女，1962年生。燕山大学机械工程学院副教授、博士。孔晓华，男，1983年生。燕山大学机械工程学院博士研究生。王耀华，男，1988年生。燕山大学机械工程学院硕士研究生。

中图分类号：TG386.1

DOI：10.3969/j.issn.1004-132X.2016.02.018