王美琴, 孙 玲, 陈怀风, 刘 瑜

山东大学密码技术与信息安全教育部重点实验室 济南 中国 250100



浅析分组密码分析方法的关联性

王美琴, 孙 玲, 陈怀风, 刘 瑜

山东大学密码技术与信息安全教育部重点实验室 济南 中国 250100

自从差分分析和线性分析相继被提出以后, 许多基于其之上的分析方法陆续出现, 各式各样的分析方法通常利用了自算法中所提取的数据的不均匀性来获取密钥的信息。人们在利用这些分析方法对分组密码的安全性进行评估时, 经常会发现一些相似的现象, 如: 某两种区分器的轮数总是相同、两种统计分析方法中所利用的统计量存在数学关系等。所以, 在建立新的分析方法的同时, 人们渐渐将关注点转移到研究各种已有的分析方法的关联性上。尽管在处理和分析方式有着形式上的不同, 但经过仔细分析之后发现许多看似不同的分析方法之间有着一些关联性, 研究这种关联性不管是从理论上还是从分析分组密码安全性的角度都是非常有必要的。近几年, 各种分析方法之间的关联性逐渐被建立起来。这些关联性的建立一方面有助于我们对已知的分组密码分析方法进行分类, 另一方面这些关联性可能会给出分组密码安全性的补充信息。本文中简要介绍了一些已有的分析方法, 并总结了已有的分析方法之间的关联性。

分组密码；分析方法；关联性

1 引言

分组密码算法现已作为许多密码元件(如: 伪随机数生成器、哈希函数等)的构造单元, 对于这些密码元件安全性的分析通常归结于对分组密码算法的攻击。在各种各样的分析方法中, 统计的分析方法通常利用了从算法中提取的数据的不均匀性来获取密钥的信息。差分分析和线性分析是统计分析方法中最基本、最重要的两种方法。

差分分析[1]最初由Biham和Shamir发表在1990年的美洲密码年会上, 此后基于此理论的研究层出不穷。直至今日, 差分分析仍是分组密码最有效的分析方法之一, 也是衡量一个分组密码安全性的重要指标。基本的差分分析利用一条高概率的差分路线(ΔA→ΔB)来恢复密钥。随着密码学的发展, 许多基于其之上的分析方法陆续被提出, 如: 截断差分分析[2]、不可能差分分析[3,4]、飞去来器攻击[5]和矩形攻击[6]等。

有些时候对某些算法不存在给定轮数的高概率差分特征, 但我们可以以较大优势决定一个分组密码算法经过一定轮数之后的一部分输出差分, 截断差分[2]正是利用这种差分特征来恢复密钥信息。不可能差分分析由Knudsen[3]和Biham[4]等人独立的提出来, 与传统差分分析基于高概率的差分特征不同,不可能差分利用不可能出现的(概率为0的)差分特征来进行区分攻击或获取密钥信息。在不可能差分中最常用的实际上是截断不可能差分, 这种不可能差分区分器与算法中S盒的选择无关。其基本的构造方法是利用中间相错的方法, 即分别以从前往后和从后往前的方式以概率为 1的方式延拓出两条截断差分特征然后使这两段差分特征中间连接的部分出现矛盾。许多文献给出了这种截断不可能差分的自动化搜索方法, 如u方法[7]、UID方法[8]。

在1993年的欧洲密码年会上, 日本学者Matsui提出了对DES算法的新的攻击方法——线性分析[9]。线性分析是一种已知明文攻击, 他通过研究明文和密文之间的线性关系来恢复密钥。经过二十几年的发展和完善, 线性分析同差分分析一样, 已经成为现代分组密码设计时必须考虑的重要设计准则。同样的, 许多建立在线性分析理论之上的分析方法也层出不穷, 如: 多重线性分析[10,11]、多维线性分析[12]、零相关线性分析[13,14,15]等。

要改进基本的线性分析, 一个自然的想法是利用多条线性路线。Matsui最先提出了这种改进, 在文献[10]中, 他同时利用了两条线性逼近改进了 DES的攻击。同年, Burton等人[11]正式的建立了基于多条线性逼近的线性分析模型, 该模型基于一个较强的假设, 即所使用的线性逼近统计独立。但 Murphy[16]指出, 这一假设一般情况下不成立。2009年, Hermelin[12]等人给出了多维线性分析的模型, 该模型避免了多重线性的模型中的独立性假设。

零相关线性分析由 Bogdanov和 Rijmen[13]于2012年首次提出, 与传统的线性分析不同, 零相关线性分析利用相关度为零的线性逼近来进行区分攻击或恢复密钥。随着零相关线性分析的提出、发展以及应用, 零相关线性分析已经成为密码分析中的一种重要工具。虽然零相关线性分析与不可能差分分析在理论和技术两方面有很大的不同, 但零相关线性分析可以看做不可能差分分析在线性分析领域的一种对偶方法。

然而基本的零相关线性分析所需要的数据量为整个明文空间或2n−1个选择明文, 其中n为分组密码算法的分组长度。一方面, 极高的数据复杂度需求极大地限制了零相关理论的应用, 另一方面由于分组密码中一般存在大量的零相关线性逼近, 对于零相关线性逼近的不充分应用也限制了零相关这一理论的发展。以此为出发点, Bogdanov和王美琴[14]在2012年提出了利用多条零相关线性逼近来进行区分攻击或密钥恢复攻击的多重零相关分析模型。假设存在ℓ条零相关线性逼近, 则多重零相关线性分析所需的数据复杂度约为。与基本的零相关线性分析相比, 多重零相关线性分析的数据复杂度显著降低。但与多重线性分析模型类似的是, 多重零相关的分析模型也基于较强的独立性假设。Bogdanov[15]等人又提出了积分零相关区分器和多维零相关线性分析新模型。多维零相关线性分析模型与多重零相关线性分析模型相比, 在维持数据复杂度基本不变的基础上, 不再依赖ℓ条零相关线性逼近相互独立这一强假设条件, 极大地完善了零相关线性分析理论。

除了差分和线性这两条基本的主线之外, 许多形式上与上述统计分析方法看似不同的统计分析方法也在密码学的发展过程中被提出, 如: 积分分析[17,18]、统计饱和度分析[19]。积分[17,18]是继差分分析和线性分析之后, 密码学界公认的最有效的密码分析方法之一。这种攻击方法更多的与算法的结构有关, 而与算法部件的具体取值关系不大, 作为主要针对面向字节运算算法安全性的密码分析方法, 积分攻击从其出现就受到密码学界的广泛关注。统计饱和度攻击[19]的主要想法是利用某些特殊的分组密码算法中较弱的扩散性, 通过固定明文比特的某些比特输入,考虑密文部分比特的分布。

人们在利用这些分析方法对分组密码的安全性进行评估时, 经常会发现一些相似的现象, 如: 某两种区分器的轮数总是相同、两种统计分析方法中所利用的统计量存在数学关系等。所以, 在建立新的统计分析方法的同时, 人们渐渐将关注点转移到研究各种已有的统计分析方法的关联性上。尽管在分析和统计方式有着形式上的不同, 但经过仔细分析之后发现许多看似不同的统计分析方法之间有着一些关联性, 研究这种关联性不管是从理论上还是从分析分组密码安全性的角度都是非常有必要的。近几年, 各种统计分析方法之间的关联性逐渐被建立起来。这些关联性的建立一方面有助于我们对已知的分组密码分析方法进行分类, 另一方面这些关联性可能会给出分组密码安全性的补充信息。

早在1994年, Chabaud和Vaudenay[20]就提出了线性分析和差分分析之间的数学关系, 但这一数学关系后来并没有实际应用于差分概率的计算, 因为直接的应用需要涉及2n+m个线性逼近相关度的计算,其中n和m分别为明文空间和密文空间的维数, 当n和m比较大时, 这种计算方法并不可行。

直到2013年的欧密会上, Blondeau和Nyberg[21]将这一数学关系进行推广, 应用到划分后的明文空间和密文空间, 得到了特定形式的截断差分的概率和多维线性中相关度之间的关系。并给出了特殊情况下, 截断不可能差分和零相关线性分析的一种等价性, 这种等价性并不依赖于分组密码的结构。同样的, 由于这种等价性的成立要求所使用的截断不可能差分的维数和零相关线性逼近的维数均为n, 所以零相关与不可能差分之间的等价性(或不等价性)并没有得到实际的解决。Blondeau和Nyberg在文献[22]中又利用推广后的数学关系给出了截断差分的概率和多维线性中容度的关系, 并将文献[23]中对于差分分析和线性分析数据复杂度的确切评估应用到截断差分和多维线性的分析中来, 得出了截断差分分析和多维线性分析各种攻击复杂度之间的关系。

2014年, Blondeau[24]等人对两类特殊的结构, Feistel结构和Skipjack结构, 给出了不可能差分区分器和零相关区分器的等价性。而后, 孙兵等人[25]将上述结论进行推广, 通过引入结构和对偶结构的概念,对Feistel结构和代换置换结构(Substitution Permutation Network, SPN)证明了不可能差分和零相关的等价关系。

另一方面虽然统计饱和度攻击对于轻量级算法PRESENT[26]给出了最好攻击, 但在文献[19]中并没有给出攻击复杂度的一种确切评估。直到2011年的欧密会上, Leander[27]证明统计饱和度分析和多维线性分析在本质上是相同的, 这种关系允许我们正确的评估统计饱和度攻击中使用的偏差, 从而确切的评估攻击的复杂度。从这一方面来讲, 研究统计分析方法之间的关系, 也有助于我们用较为完善的理论体系丰富和发展密码体系中较为薄弱的环节。后来Blondeau和Nyberg在文献[22]通过对截断差分分析和统计饱和度分析中所使用的统计量的观察, 发现这两种统计量只相差一个常数, 从而证明截断差分分析和统计饱和度分析在本质上是相同的。

零相关分析和积分分析之间的关系最早由Bogdanov等人[15]提出, 作者给出了特定形式的零相关区分器与积分区分器之间的等价关系。文献[15]指出: 积分区分器可以无条件的转换为一个零相关区分器, 而当零相关区分器转换为积分区分器时要求零相关区分器的输入掩码和输出掩码相互独立。后来, 孙兵等人[25]证明一个零相关区分器可以无条件的转换为一个积分区分器, 从而去掉了[15]中的独立性要求。除此之外, 作者还证明[15]中给出的―积分区分器可以无条件的转换为零相关区分器”这一结论仅适用于平衡向量布尔函数的积分性质, 但这并不是一般使用的积分性质。对于积分区分器和不可能差分区分器之间的等价关系, 文献[25]中也给出了相关结果。

作为差分分析的两种推广——不可能差分分析和截断差分分析之间的关系的研究, 李雷波等人[28]也做出了一些结果。他们通过将截断不可能差分中间相错的关键步骤以一定的概率转换为中间相遇,从而将不可能差分转变为截断差分, 并给出了这种截断差分的概率计算公式。得益于截断不可能差分的自动化搜索方法, 这一关系的发现将可能有助于促进截断差分搜索的自动化。

我们在图1中给出上述的所有关系。

本文剩下的部分将详细介绍分组密码不同分析方法之间的关联性。第二节将简要介绍分组密码的不同分析方法并给出一些符号定义。第三节关注基本的线性分析与基本的差分分析之间的关系。第四节详细阐述了多维线性、截断差分和统计饱和度攻击之间的关联性。第五节给出零相关、不可能差分和积分攻击之间的关系。第六节介绍了由不可能差分向截断差分的转换。第七节进行总结。

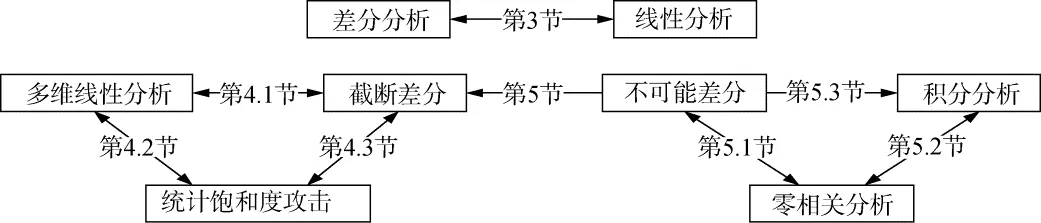
图1 分组密码统计分析方法的关联性

2 分组密码不同分析方法简介

差分分析和线性分析是分析分组密码安全性的两种重要手段。基于这两种基本的统计分析方法, 许多新的统计分析方法又陆续被提出。本节我们将简要的介绍一些后面分析会用到的统计分析方法。

2.1 分组密码的差分分析方法综述

2.1.1 基本的差分分析

差分分析[1]最初由Biham和Shamir发表在1990年的美密会上, 此后基于此理论的研究层出不穷。直至今日, 差分分析仍是分组密码最有效的分析方法之一, 也是衡量一个分组密码安全性的重要指标。

设X和X′为两个长度为n的比特串, X和X′的差分定义为

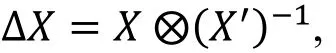
其中⊗为比特串的运算并且该运算取决于密钥介入的方式, X−1为X关于运算⊗的逆。基本的差分分析基于在密钥介入前后, 中间状态的差分相同, 然而在一个加密算法中, 总存在相对于⊗运算是非线性的运算。差分分析利用了如下观测: 对于一个确定的输入差分, 输出差分的分布是不均匀的。

定义 1(差分路线).

一个s轮的差分路线为一个s+1元数组*β0,β1,…,βs+, 其中ΔP=β0,ΔCi=βi(1≤i≤s)。

设pi是输入差分为βi−1输出差分为βi的概率。文献[29]中引入了Markov密码的概念, 在Markov密码中这一概率与轮函数的具体输入无关并且遍历所有轮密钥的可能取值得到。并且他们证明在Markov密码中若轮密钥Ki是相互独立的, 则pi也相互独立并且有

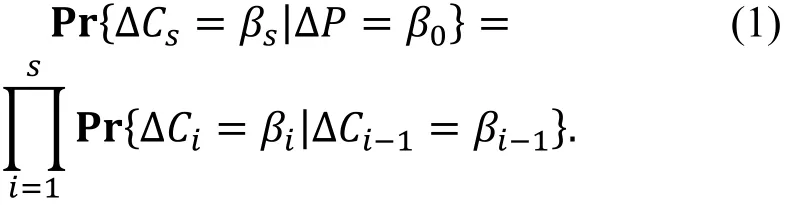
大量的实验证明等式⑴确实是差分特征概率计算的一个好的近似。我们称s轮的差分路线为一个区分器, 在具体的攻击时, 通常在区分器前后分别加几轮, 然后利用一定数量的选择明密文对恢复这几轮中涉及的部分密钥。

在各种各样的统计分析方法中, 通常会涉及两类错误概率:

1. 正确密钥被当作错误密钥的概率(α0),

2. 错误密钥被当作正确密钥的概率(α1)。

而攻击的成功率PS=1−α0。统计攻击中常常会涉及信噪比、优势的概念。

定义 2(差分分析中的信噪比).

差分分析的密钥恢复阶段, 我们枚举选择明密文对对候选密钥进行推荐, 信噪比定义为: 正确密钥被推荐的次数与随机选择的错误密钥被推荐的次数之比。

定义 3(优势).

对于针对k比特密钥的密钥恢复攻击, 优势为a指的是正确密钥位于前2k−a个候选密钥当中。

对于优势a, 我们有α1=2−a。

文献[23]中给出了攻击的成功率PS, 数据量N和优势a之间的数量关系:

定理 1( [23, 定理3] ).

对于一个关于针对k比特密钥的差分攻击, 所利用的差分特征的概率为p, 设PS为攻击的成功率, SN为信噪比, N为攻击中使用的明密文对的数量, a为攻击的优势。假设密钥的计数器是独立的并且它们对于所有的错误密钥同分布, 则对有充分大的k和N有,

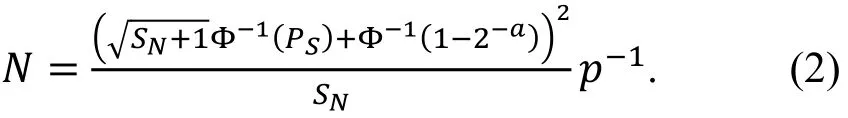
由等式⑵我们可以看出, 差分攻击中所需的选择明密文对的个数正比于。

注意到虽然这一差分路线是固定的, 但在区分攻击或密钥恢复攻击中我们只利用了这一路线输入差分和输出差分的信息, 而且当输入差分和输出差分固定时, 这样的差分路线通常不止一条, 这就引出了差分特征的概念。

定义 4(差分特征).

我们称差分对β0→βs为一个s轮差分特征, 其中ΔP=β0,ΔCs=βs。这一差分特征的概率定义为

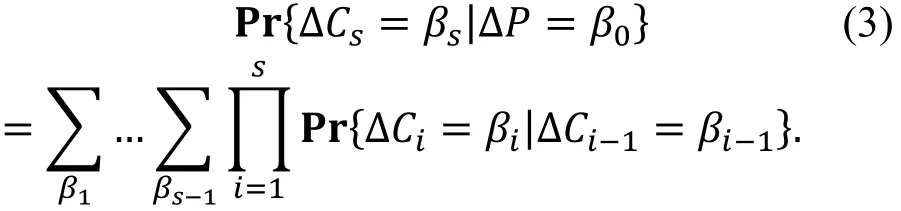
由差分路线概率的计算公式⑴和差分特征概率的计算公式⑶的比较我们可以看出: 差分特征的概率一般大于等于相应的一条差分路线的概率。

2.1.2 截断差分

与基本的差分分析不同, 有些时候确定所有比特上的高概率差分特征是困难的, 但我们可以以较大优势决定一个分组密码算法经过一定轮数之后的一部分输出差分, 截断差分[2]正是利用这种差分特征来恢复密钥信息。文献[2]中给出了截断差分的确切定义。

定义5(截断差分).

一个部分已知的n比特差分称为截断差分。形式的有, 设(α,β)为一个r轮差分, 若Γα为α构成的集合,Γβ为β构成的集合, 则称Γα→Γβ为一个r轮的截断差分。

在进行统计分析方法关联性分析的过程中我们常常需要对明密文空间进行划分。一个n比特的加密算法, 通常划分为下面的形式(如图2所示)

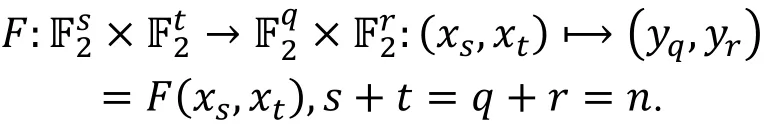
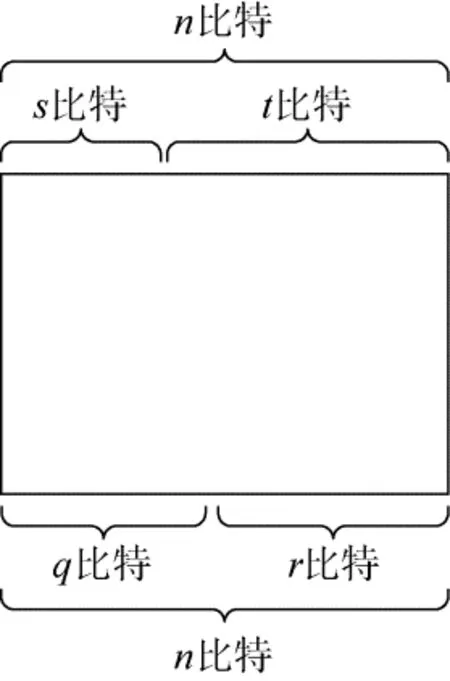
图2 分组密码明密文空间的划分

在具体的应用中, 我们所使用的截断差分的输入差分和输出差分将满足一定的结构特性, 如构成线性空间。由于本文中只讨论这种情况, 所以我们在下面给出一些符号说明。

设截断差分的输入有2t种可能且形式, 有2r种可能的输出差分且其形式为, 即共考虑2t+r个不同的差分特征。我们知道输入差分为(0,δt)、输出差分为(0,Δr)的确定的差分特征, 其概率为

2.1.3 不可能差分

不可能差分分析由Knudsen[3]和Biham[4]等人独立的提出来, 与传统差分分析基于高概率的差分特征不同, 不可能差分分析利用不可能出现的差分特征来进行区分攻击或恢复密钥信息。在不可能差分中最常用的实际上是截断不可能差分, 这种不可能差分区分器与算法中S盒的选择无关。其基本的构造方法是利用中间相错的方法, 即分别以从前往后和从后往前的方式以概率为 1 的方式延拓出两条差分特征然后使这两段差分特征中间连接的部分出现矛盾。如图 3所示, 我们将加密算法E分解为E=E1∘E0, 对E0存在概率为 1的截断差分Γ0→Γ1,对E−1存在概率为1的截断差分Γ2→, 如果Γ1与不重合, 则Γ0→Γ2构成了E的一个不可能差分区分器。许多文献给出了这种截断不可能差分的自动化搜索方法, 如u方法[7]、UID方法[8]。在进行密钥恢复攻击时, 若部分加解密得到的中间状态差分满足了该不可能差分, 则可以将这一候选密钥排除。

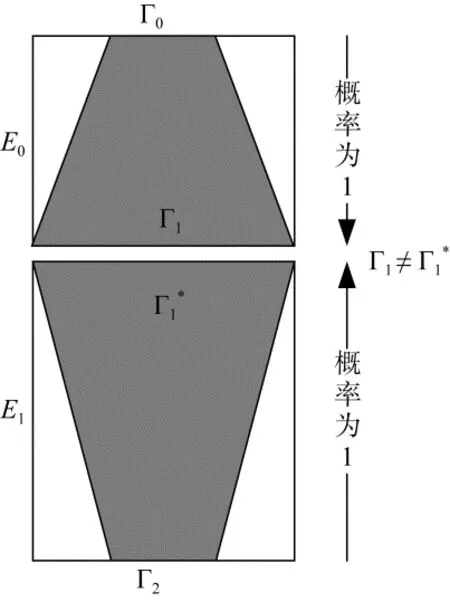
图3 分组密码不可能差分区分器的构造

2.2 分组密码的线性分析方法综述

在1993年的欧密会上, 日本学者Matsui提出了对 DES算法的一种新的攻击方法—―线性密码分析”[9]。线性分析是一种已知明文攻击方法, 它通过研究明文和密文之间的线性关系来恢复密钥。经过十几年的发展和完善, 线性分析已经成为现代分组密码设计时的重要设计准则之一。

2.2.1 基本的线性分析

线性攻击的基本思想是攻击者希望找到一个形如⑷的线性表达式,并且该表达式成立的概率与之间的差距足够大,

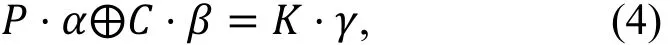
其中―·”表示标准的内积运算, α称为输入掩码, β称为输出掩码, 这样的一个表达式称为一条线性路线。简单来说, 我们期待在明文比特和密文比特之间找到一个概率线性关系, 即存在一个比特子集使得其中元素的异或和表现出非随机的分布。

一条线性路线的强弱可以用相关度的概念来衡量。

定义6(布尔函数的相关度).

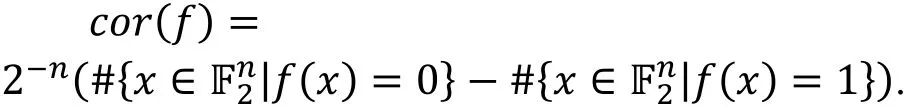
定义7(线性逼近的相关度).

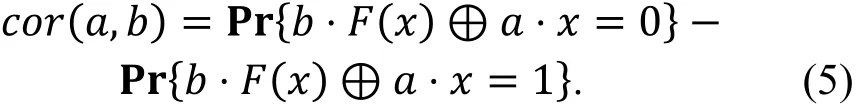
与相关度相关的一个概念是函数的傅里叶变换

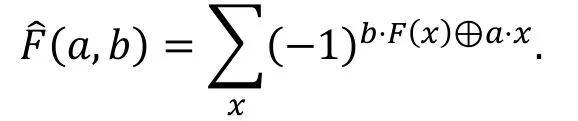
由上面的定义, 我们有

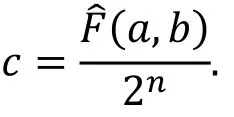
线性路线的偏差ε与相关度c满足c=2ε。

给定一条形如⑷的线性路线(不失一般性, 假设偏差为正)和N个明文, 可以用下面的过程恢复部分密钥信息。

1. 遍历所有的明文, 记录使得等式⑷左侧等于0的明文个数T。

2. 若T＞N/2, 则猜测K·γ=0; 否则, 猜测K·γ=1。

通过上述攻击我们可以得到关于密钥的一比特信息K·γ。

在实际的攻击中, 我们通常将高偏差的线性逼近放在被攻击算法的中部, 猜测部分密钥后, 通过从前往后(从后往前)部分加(解)密得到中间状态的值,并由此判断线性表达式成立与否。这种攻击过程与上述攻击过程基本类似, 但由于部分加解密的过程需要牵扯到对部分子密钥的猜测, 我们对每个猜测密钥建立计数器并记录线性表达式成立的次数, 按照相关度从大到小的顺序对候选密钥进行排序。文献[23]中给出了成功率PS, 数据量N和优势a之间的数量关系:

定理2( [23, 定理2] ).

设PS为攻击的成功率, 攻击中所使用的线性路线的偏差为ε, 对于一个针对k比特密钥的线性攻击,所利用的线性路线的偏差为ε, 设PS为攻击的成功率, N为攻击中使用的明文的数量, a为攻击的优势, 假设线性路线是否成立关于密钥独立, 则有

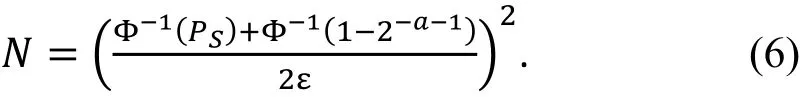
注意到等式⑷的右侧确定了一条线性路线内部状态的掩码, 但在进行攻击时, 我们并没有对线性路线的内部做要求, 所以与差分分析中差分特征的概念类似, 线性分析中也存在线性壳的概念。文献[30]中作者基于下面的定理给出了线性壳的概念, 令为关于X和K的随机变量。

定理3 ( [30, 定理1] ).

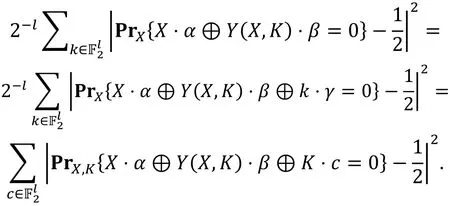
称线性路线族

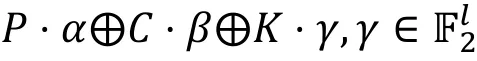
为分组密码算法的线性壳。从上述定理中我们可以得到线性壳的偏差与相对应的线性路线的偏差间的关系, 但由于这种线性壳偏差的计算需要遍历整个密钥空间, 而算法分析的情境通常是在一个固定密钥下的, 所以该公式并不能实际的用来计算线性壳的偏差。当前计算线性壳偏差的方式是将所有输入掩码、输出掩码相同的线性路线的偏差(带符号)相加, 即便如此, 有时因为所涉及的线性路线条数较多, 而大多数的线性路线的偏差绝对值较小, 我们通常只取其中的一条或几条偏差绝对值较大的线性路线作为代表近似地计算线性壳的偏差。

2.2.2 多重线性分析

要改进基本的线性分析, 一个自然的想法是利用多条线性路线。Matsui最先提出了这种改进, 在文献[10]中, 他同时利用了两条线性逼近改进了 DES的攻击。同年, Burton等人[11]建立了基于多条线性逼近的线性分析模型, 该模型基于一个较强的假设,即所使用的线性逼近统计独立。

假设我们可以得到m条相互独立的、偏差有优势的线性逼近, 与基本的线性分析类似, 我们对每一条线性逼近统计使得该线性逼近成立的明文个数Ti,i=1,2,…,m, 然后利用Ti计算下面的统计量C

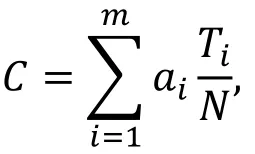
其中ai为对应线性逼近的权重, 文献[11]中证明, 当ai与其对应的线性路线的偏差成比例时, 统计量C的区分优势最大。并在统计量之下给出了多重线性分析所需明文量N的计算公式。

定理4 ( [11, 定理3] ).

在独立性的假设之下, 多重线性分析的成功率为

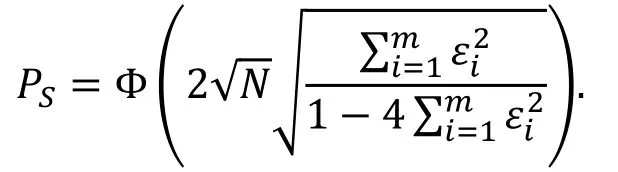
到目前为止, 多重线性分析所需的数据量N并没有更好的计算公式。注意到与之前差分分析和线性分析数据量N的计算公式不同, 这里的公式并没有涉及优势a, 这是由于作者默认统计量C最大的密钥为正确密钥。

2.2.3 多维线性分析

注意到在多重线性分析模型建立在线性逼近统计独立的假设之上, 但 Murphy[16]指出这一假设一般情况下不成立。2009年的FSE会议上, Hermelin等人[12]给出了多维线性分析的模型, 该模型避免了多重线性模型中的独立性假设。

同截断差分一样, 在多维线性分析的具体的应用中, 我们所使用的线性逼近输入掩码和输出掩码满足一定的结构特性, 本文中只讨论其构成线性空间的情况。这里我们仍利用图 2中给出的明密文空间的划分, 设多维线性区分器的输入掩码有2s种可能的情况且形式为(as,0)∈×*0+, 输出掩码有2q可能的情况且形式为(bq,0)∈×*0+, 即共考虑2s+q个不同的线性逼近。

多维线性区分器的强度可以用容度的概念来刻画,上述多维线性区分器的容度定义为

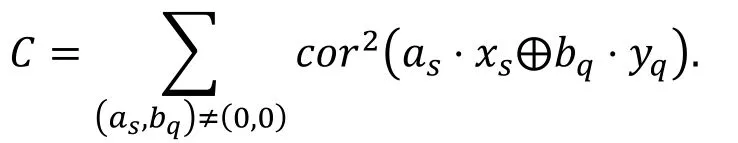
容度也可以用(xs,yq)的概率分布与上的均匀分布之间的L2距离来计算[31], 严格的说, 假设(xs,yq)的分布为

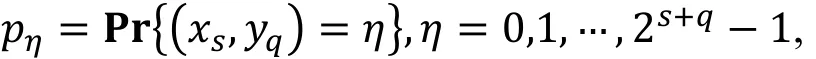
则容度为

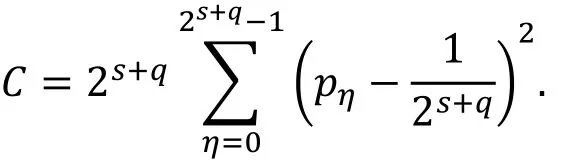
根据分析中所使用的统计量的不同, 多维线性分析又可以分为卡方方法和LLR方法。由于本文的讨论并不涉及多维线性分析的具体分析过程, 这里不做过多介绍。

2.2.4 基本的零相关线性分析

零相关线性分析由 Bogdanov和 Rijmen[13]于2012年首次提出, 与传统的线性分析不同, 零相关线性分析利用相关度为零的线性逼近来进行区分攻击或恢复密钥。虽然零相关线性分析与不可能差分分析在理论和技术两方面有很大的不同, 但零相关线性分析可以看做不可能差分分析在线性分析领域的一种对偶方法。

利用零相关线性逼近进行分组密码算法与随机置换的区分时, 需要计算给定线性逼近的相关度。通常的计算方法是遍历所有的明文输入, 计算相应的输出, 从而求得给定线性逼近的相关度。对于分组密码的零相关线性逼近求相关度, 求得的相关度一定为0, 但对于随机置换, 有下面的命题:

命题1 ( [13, 命题3] ).

对n比特置换函数上非平凡的线性逼近相关度为0的概率可以如下近似计算

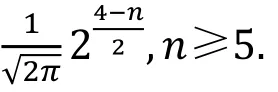
根据这一命题, 我们可以确定最终密钥候选的数量, 最后用一定数量的明密文对对候选密钥进行筛选, 唯一确定正确密钥。

2.2.5 多重零相关线性分析

基本的零相关线性分析所需要的数据量为整个明文空间或2n−1个选择明文, 其中n为分组密码算法的分组长度。一方面, 极高的数据复杂度需求极大地限制了零相关理论的应用, 另一方面由于分组密码中一般存在大量的零相关线性逼近, 对于零相关线性逼近的不充分应用也限制了零相关的发展。以此为出发点, 为降低零相关线性分析模型中的数据复杂度, Bogdanov和王美琴[14]在2012 年的FSE会议上提出了利用多条零相关线性逼近来进行区分攻击或密钥恢复攻击, 以此来降低数据复杂度。

多重零相关线性分析的出发点是利用较少的数据量来估计大量线性逼近的相关度, 建立统计量来区分正确密钥与错误密钥。模型构建中的一个基本问题是对两个正态分布的区分。假设已知样本s取自正态分布N(μ0,σ0)或N(μ1,σ1), 其中μ0和μ1为正态分布的均值, σ0和σ1为标准差, 不失一般性, 假设μ0＜μ1, 需要判断样本来自哪个正态分布。判定的方法是选定一个阈值τ, 若s≤τ, 则判定s∈N(μ0,σ0); 否则判定s∈N(μ1,σ1)。这样存在两类错误概率

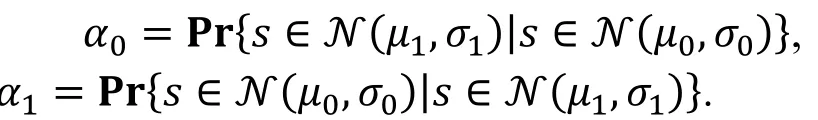
假设攻击者拥有N个已知明文, ℓ条零相关线性逼近, 假设Ti,1≤i≤ℓ, 是N个明文中满足第i条线性逼近的个数, 计算下面的统计量

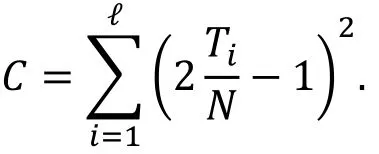
多重零相关线性分析模型的建立基于下面的命题

命题2 ( [14, 命题2、3] ).

设有分组密码算法上的ℓ个非平凡零相关线性逼近和N个已知明文, 设Ti,1≤i≤ℓ是N个明文中满足第i条线性逼近的个数。假设Ti之间相互独立, 则对足够大的ℓ,N和n, 在正确密钥下

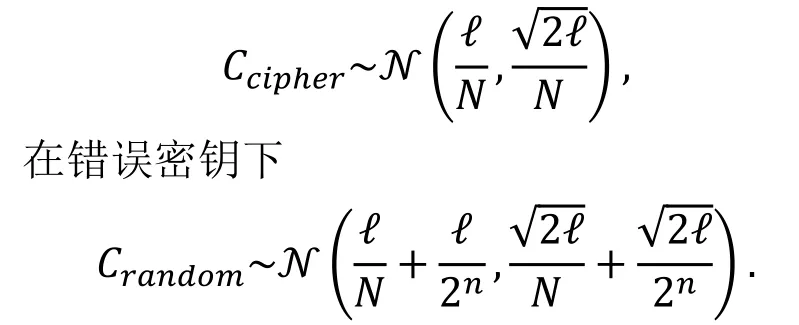
命题3 ( [14, 定理1] ).

用ℓ个非平凡的零相关线性逼近, 以错误概率α0(正确密钥当成错误密钥的概率)和α1(错误密钥当成正确密钥)来区分正确密钥和错误密钥, 需要的已知明文的个数需满足如下关系:

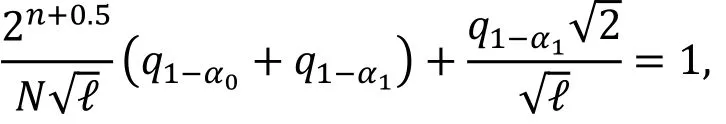
由命题 3可知, 假设存在ℓ条零相关线性逼近,则多重零相关线性分析所需的数据复杂度约为。与基本的零相关线性分析相比, 多重零相关线性分析的数据复杂度显著降低。

2.2.6 多维零相关线性分析

虽然多重零相关线性分析的数据复杂度较之前基本的零相关线性分析显著降低, 然而, 多重零相关的分析模型与多重线性分析模型类似, 基于一个强烈的假设, 即要求所使用的ℓ条零相关线性逼近相互独立, 这一条件通常难以满足。在2012年的亚洲密码年会上, Bogdanov[15]等人提出积分零相关区分器和多维零相关线性分析新模型。多维零相关线性分析模型与多重零相关线性分析模型相比, 在维持数据复杂度基本不变的基础之上, 不再依赖ℓ条零相关线性逼近相互独立这一强假设条件, 极大地完善了零相关线性分析理论。

设(αi,βi), 1≤i≤m为→上的m个相互独立的线性逼近, 记x∈为明文, y∈为加密过程中的部分中间状态值, 用一对(x,y)对m个(αi,βi)求值, 得到m比特的值, 记为zi, 1≤i≤m:

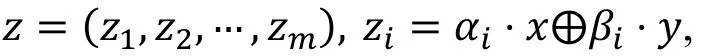
多维零相关线性分析考虑z的概率分布。设在N个明密文对下, 利用计数器V,z-记录z出现的次数,经过分析有: 在正确密钥下, V,z-服从多变量超几何分布; 在错误密钥下, V,z-服从多项分布。

利用V,z-构造统计量T

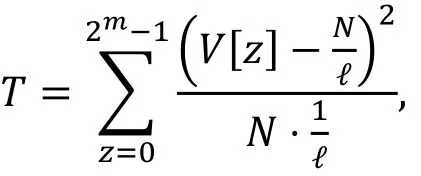
通过概率统计中的相关知识, 我们有下面的命题:

命题4 ( [15, 命题2] ).

设可以得到N个明密文对以及ℓ条零相关线性逼近, 则统计量T服从χ2分布。在正确密钥下, 其期望和方差为

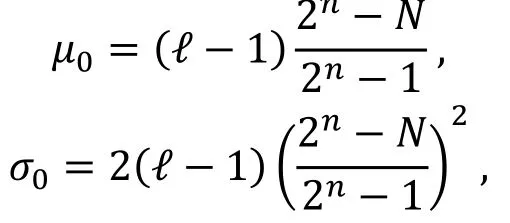
在错误密钥下, 其期望和方差为

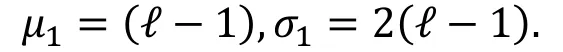
推论1( [15, 推论2] ).

n比特的分组密码算法的ℓ条零相关线性逼近构成了一个log2ℓ维的线性空间, 以错误概率α0(正确密钥当成错误密钥的概率)和α1(错误密钥当成正确密钥)来区分正确密钥和错误密钥, 需要的已知明文个数需满足如下关系:

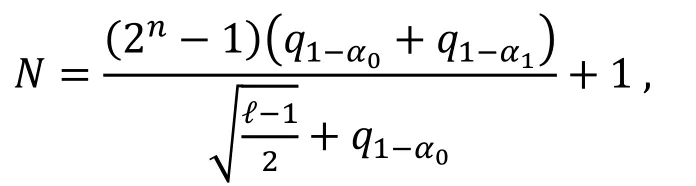
2.3 分组密码的其他分析方法

除了差分和线性这两条基本的主线之外, 许多形式上与上述统计分析方法看似不同的统计分析方法也在密码学的发展过程中被提出来, 这里我们只简要介绍两种: 积分攻击和统计饱和度攻击。

2.3.1 积分分析

积分区分器首先由Kundsen[17]在攻击Square算法时提出的, 由于这个原因, 积分区分器[18]也称为Square区分器。积分是继差分分析和线性分析之后,密码学界公认的最有效的密码分析方法之一。最初的攻击方法更多的与算法的结构有关, 而与算法部件的具体取值关系不大, 作为主要针对面向字节运算算法安全性的密码分析方法, 积分攻击从其出现就受到密码学界的广泛关注。

积分分析中经常会涉及到平衡性的概念。

定义8 (平衡性).

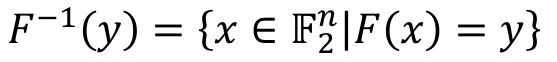
的大小与y无关。

积分攻击考虑一系列状态求和, 考虑到二元域上, 差分的定义对应为两个元素求和, 因此积分攻击可以看做差分攻击的一种推广。最初的积分区分器基于如下观测: 在固定明文的一些比特, 遍历明文的另外一部分比特时, 得到的密文的一些比特是平衡的。传统的积分攻击方法对基于比特运算的算法是无效的, 有鉴于此, Z‘aba等人在文献[32]中提出了基于比特的积分攻击方法, 其实质为一种计数方法, 通过分析特定比特位置上元素出现次数的奇偶性来确定这一比特的积分特性, 此时的积分特性通常表现为这些比特位置的异或和为常数(通常为0)。

2.3.2 统计饱和度攻击

统计饱和度攻击[19]主要想法是利用某些特殊的密码算法中较弱的扩散性, 通过固定明文的某些比特, 考虑密文部分比特的分布。

给定一个加密函数

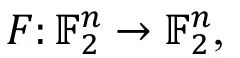
统计饱和度攻击考虑当F的输入部分固定时, 其输出的分布。这里我们同样考虑对明文空间和密文空间的分割,

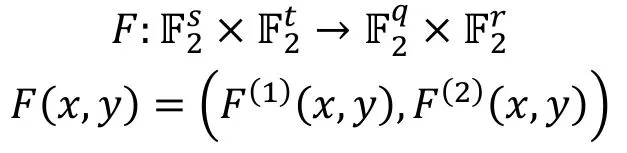
为了方便, 另hy表示将F输入的后t比特固定为y, 且在输出的前q维空间上的限制, 即:

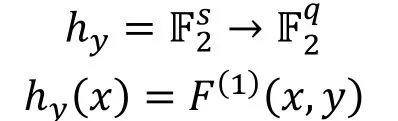
在统计饱和度攻击中我们需要考虑hy的容度Cℎ, 而攻击所需的数据复杂度为。

虽然统计饱和度攻击对于轻量级算法PRESENT[26]给出了最好攻击, 但文献[19]中并没有给出容度的Cℎ的计算公式, 从而攻击的复杂度并不能确切的评估。直到2011年的欧密会上, Leander[27]证明统计饱和度攻击与多维线性攻击在本质上是相同的, 这种关系允许我们正确的评估统计饱和度攻击中使用的容度, 从而更准确的衡量攻击的复杂度。作者利用统计饱和度攻击和多维线性攻击之间的关系, 给出了Cℎ的理论计算公式。

定理5 ( [27, 定理5] ).

统计饱和度攻击中的平均容度与线性逼近的相关度有如下关系:

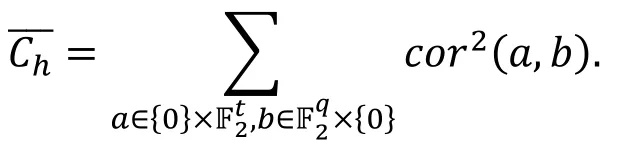
人们在利用各种统计分析方法对算法的安全性进行评估时, 经常会发现一些相似的现象, 如: 某两种区分器的轮数总是相同的、两种统计分析方法中所利用的统计量存在数学关系等。所以, 在建立新的统计分析方法的同时, 人们渐渐将关注点转移到研究各种已有的统计分析方法的关联性上。尽管在分析和统计方式有着形式上的不同, 但经过仔细分析之后发现许多看似不同的统计分析方法之间有着一些关联性, 研究这种关联性不管是从理论上还是从分析分组密码安全性的角度都是非常有必要的。近几年, 各种统计分析方法之间的关联性逐渐被建立起来。这些关联性的建立一方面有助于我们对已知的分组密码分析方法进行分类, 另一方面这些关联性可能会给出分组密码安全性的补充信息。后面我们将分四节介绍已有的统计分析方法之间的关联性。

3 差分与线性分析

早在1994年, Chabaud和Vaudenay[20]就提出了线性分析和差分分析之间的数学关系, 他们严格的证明了差分分析中差分特征的概率与线性分析中线性逼近的相关度之间的数学关系。

定理6 ( [20, 定理1] ).

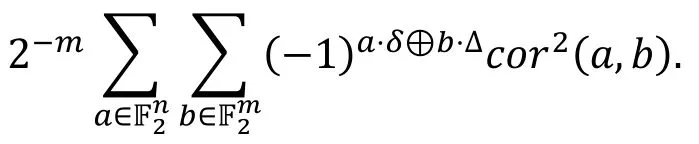
但这一数学关系后来并没有实际应用于差分概率的计算, 因为直接的应用需要涉及2n+m个相关度的计算, 当n和m都比较大时, 这种计算方法是不可行的。直到2013年的欧密会上, Blondean和Nyberg[21]将这一数学关系进行推广, 应用的划分后的明密文空间, 得到了特定形式的截断差分的概率与多维线性中容度之间的关系。

定理7 ( [21, 定理3] ).

对任意的δs∈,Δq∈下面的式子成立

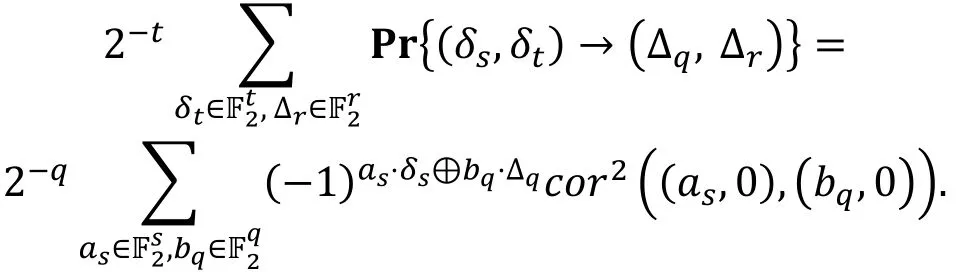
利用这一关系, 作者令q=t, 使所有非平凡的线性逼近的相关度和差分的概率为零, 导出了特殊情况下, 截断不可能差分和零相关线性分析的一种等价性, 注意到这种等价性并不依赖于分组密码的结构。

推论2( [21, 推论2] ).

但正如文献[24]中指出的那样, 虽然这一等价性与底层算法的结构无关, 但对于大多数的不可能差分区分器和零相关区分器, 推论 2并不能直接应用,因为这一等价性的成立需要满足区分器的维数为n,即区分器包含2n个不可能差分特征或零相关路线。对于大多数算法而言, 只有极少数的不可能差分和零相关路线, 所以零相关与不可能差分之间的等价性并没有得到实际的解决。

由于线性分析与差分分析的攻击条件不同(线性分析为已知明文攻击, 差分分析为选择明文攻击),研究二者之间的关联性有助于我们选择更适合攻击的区分器进行算法攻击。但因为现存的数学关系不能有效的应用, 所以二者之间更实用的关联性有待进一步发掘。

4 多维线性、截断差分与统计饱和度攻击

4.1 多维线性与截断差分

Blondeau和Nyberg[22]进一步应用定理7的结论,考虑令δs=0,Δq=0, 而不对线性逼近的相关度和差分概率做假设, 得到了特定形式(见图 4)的截断差分概率与多维线性容度之间的关系。

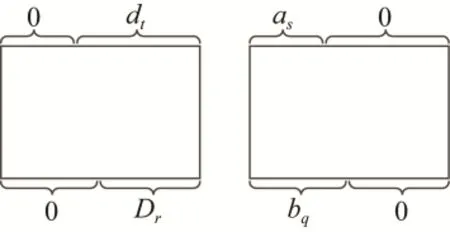
图4 多维线性区分器与其对应的截断差分

推论3( [22, 推论1] ).

为导出多维线性分析和截断差分分析在攻击时数据复杂度的关联性, 作者分别利用定理 1和定理2给出了利用上述截断差分和多维线性区分器进行攻击时的数据复杂度。

命题5( [22, 命题2] ).

假设上述截断差分的概率为p, 攻击的成功率为50%, 优势为a比特, 则攻击所需的数据量为

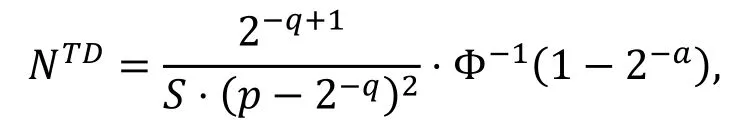
其中S为每个结构体(在差分分析中, 为了以较大的效率利用选择的明密文对, 通常会构造结构体(structure))中选择明文的数量。

命题6( [22, 命题1] ).

假设上述多维线性逼近的容度为C, 则利用其进行攻击时所需的数据量为

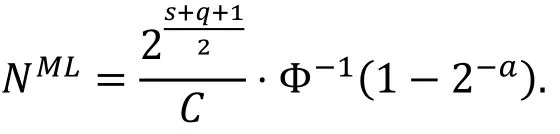
命题 5、6结合上推论 3, 作者得到了上述多维线性和截断差分分析数据量之间的关系。

推论4( [22, 推论2] ).

上述截断差分与多维线性分析中所使用的数据量满足下面的关系:

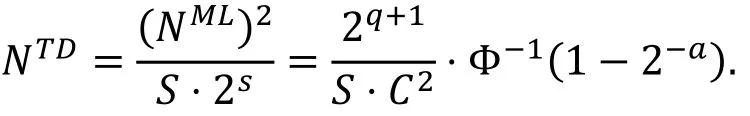
特别的, 当S=2t时, 我们有

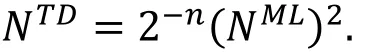
现存的截断差分分析和多维线性分析攻击时所使用的数据量之间的关系可以帮助我们判断哪一种攻击方法更适用于目标算法。另一方面, 二者在攻击方式上的不同使得我们可以通过将截断差分区分器转换为相应的多维线性区分器, 从而将选择明文的要求降低为已知明文。不过由于现存的等价性不依赖与算法的内部结构, 所以这种等价性虽具有一般性, 但欠缺实用性。这是因为这种等价性要求截断差分非零的部分与多维线性非零的部分互补, 这就使得若其中一种区分器的维数比较小, 另一种区分器的维数会非常大, 这种区分器在密钥恢复阶段并不具备优势。

4.2 多维线性与统计饱和度

在2.3.2节关于统计饱和度攻击的介绍中, 定理5给出的平均容度与相关度的数学关系说明统计饱和度攻击与多维线性攻击在本质上是相同的, 这种关系允许我们对统计饱和度攻击复杂度做一个更为准确的评估。从这一方面来讲, 研究统计分析方法之间的关系, 也有助于我们用较为完善的理论体系丰富和发展密码体系中较为薄弱的环节。

4.3 截断差分与统计饱和度

Blondeau和Nyberg[22]通过对截断差分分析和统计饱和度分析中所使用的统计量的观察, 发现这两种统计量只相差一个常数, 从而证明截断差分分析和统计饱和度分析在本质上也是相同的。

5 零相关、不可能差分与积分攻击

5.1 零相关与不可能差分分析

对于以字为单位的分组密码, 零相关和不可能差分分析是两种非常有效的攻击方法。尽管在密钥恢复阶段这两种分析方法存在一些差异, 但这两种区分器通常会覆盖相同的轮数。然而在一些特殊的情况下, 这两种区分器的轮数并不相同。文献[20]中给出了特定形式的零相关区分器和不可能差分区分器之间的数学关系(上述推论 2), 这一数学关系并不依赖与分组密码的结构, 正如文献[24]中所指出的那样, 虽然这一数学关系与底层的算法结构无关, 但对于大多数的不可能差分区分器和零相关区分器,推论 2并不能直接应用, 因为这一数学关系需要满足区分器的维数为n, 即区分器包含2n个不可能差分特征或零相关区分器。对于大多数算法而言, 只有极少数的不可能差分路线或零相关路线, 所以零相关与不可能差分之间的等价性或不等价性并没有得到实际的解决。

Blondeau等人在文献[24]中解决了对于 Feistel和 Skipjack类型的分组密码算法这两种分析方法的条件等价性, 由于这种等价性考虑了分组密码的结构, 所以这一结论虽不具有一般性, 但更具实用性。首先对广义 Feistel结构, 作者利用矩阵方法给出了零相关与不可能差分的等价条件。在描述这些关联性之前, 我们首先给出一些基本的符号表示。

令n为面向字结构的分组密码算法的分组长度,算法的每个状态有b个字, 每个字的长度为s, 即有n=b·s。n比特的状态X可以表示为X=(X1,X2,…,Xb), 每个Xi的长度为s。对于 Feistel结构的算法, 其轮函数满足: 每一个输入分支或者可以是一个非线性函数的输入或者与一个这样的非线性函数的输出异或, 通常可以表示为一个非线性层(F层)和一个线性层(P层)。

定义9( [24, 定义1] ).

不考虑密钥和常数加的过程, 具有b个分支的Feistel结构算法的轮函数可以表示为两个b×b的矩阵ℱ、P的组合, 其中ℱ和P矩阵中元素由*0,1,Fi+构成, 其中*Fi+i≤I表示轮函数中的非线性函数。

· 非线性层表示(ℱ层): 矩阵ℱ对角线上的元素为1;如果函数Fi的输入为第k分支, 其输出与第j分支进行异或, 将ℱ矩阵的第j行第k列设置为Fi; 其他元素为 0。这同时意味着在每一行每一列中至多含有一个Fi。

· 置换层表示(P层): 矩阵P是一个置换矩阵, 在每一行每一列中只有一个非零元素。

则一个 Feistel结构的轮函数可以表示为上面的两个矩阵的组合, 即R=P·ℱ。

用矩阵定义的Feistel结构来表示r轮的不可能差分Γ0→Γ1, 则存在l和m(l+m=r)使得输入差分Γ0正向传播l轮得到的与输出差分Γ1逆向传播m轮得到的存在着不一致的部分, 也就是:

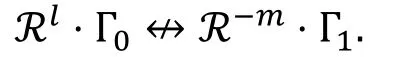
定义10( [24, 定义2] ).

对于给定轮函数R=P·ℱ的Feistel结构的算法,我们定义R的镜像函数为ℳ=P·ℱT, 其中ℱT为函数ℱ的转置。

Blondeau等人在下面的定理中给出了Feistel结构算法的零相关路线和不可能差分路线的等价条件。

定理8( [24, 定理] ).

令R为 Feistel结构算法的轮函数的矩阵表示,ℳ为R的镜像矩阵, 如果存在一个b×b的置换矩阵Z满足:

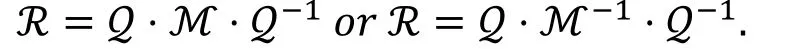
我们可以得出: 分组算法存在m条r轮的不可能差分路线构成的不可能差分区分器当且仅当该分组算法也存在m条r轮零相关路线构成的零相关区分器。

Skipjack类型的算法轮函数中的非线性函数的输入输出在同一个分支上, 非线性函数部分为F层;在F层后将不同分支的状态进行线性操作的部分为X层; 最后一个分支位置的置换层P层, 其矩阵定义如下。

定义11( [24, 定义3] ).

对于具有b个分支的Skipjack类型的算法, 其轮函数可以表示为3个b×b矩阵G、χ、P的组合, 这些矩阵中的元素在*0,1,F+中取值, 其中F表示非线性操作。

·F层表示: 函数G的对角线上元素为1或F, 如果非线性操作F作用到第j分支上, 则矩阵G的第j个对角元素为F。

· X层表示: 矩阵χ在对角线上的元素为 1, 而且每行每列至多两个1。

· P层表示: 矩阵P是一个置换矩阵, 每行每列只有一个非零元素。

则一个 Skipjack类型的算法轮函数可以表示为一个b×b的矩阵R=P·χ·G。

定义12( [24, 定义4] ).

给定轮函数为R=P·χ·G的 Skipjack 类型算法, 该轮函数的镜像函数为ℳ=P·χT·G。

对于 Skipjack类型的分组算法, 下面的定理给出了零相关和不可能差分等价的条件。

定理9( [24, 定理2] ).

R为Skipjack类型算法的轮函数矩阵表示, ℳ为R的镜像函数矩阵表示, 如果存在一个b×b的置换矩阵Z满足:

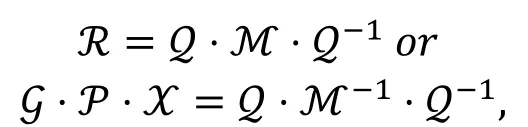
我们可以得出: 分组算法存在m条r轮的不可能差分路线构成的不可能差分区分器当且仅当该分组算法也存在m条r轮零相关路线构成的零相关区分器。

对于其他的一些具有广义 Feistel结构的算法,也存在类似定理8和定理9的结论。

定理10( [24, 定理3] ).

R=P·χ·ℱ为广义 Feistel结构算法的轮函数矩阵表示, ℳ为R的镜像函数矩阵表示ℳ=P· χT·ℱT, 如果存在一个b×b的置换矩阵Z满足:

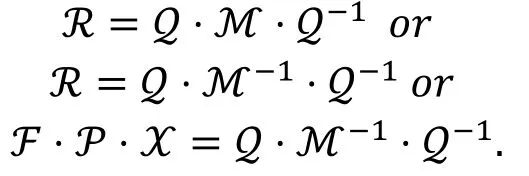
我们可以得出: 分组算法存在m条r轮的不可能差分路线构成的不可能差分区分器当且仅当该分组算法也存在m条r轮零相关路线构成的零相关区分器。

在2015年的美洲密码年会上, 孙兵等人[25]对具有SP结构的Feistel算法以及SPN结构的算法的零相关分析和不可能差分分析之间的联系进行了研究。首先给出一类算法的定义。

定义13( [25, 定义2] ).

定义14( [25, 定义3] ).

令ℱSP为分支数为2的、具有SP结构轮函数的Feistel结构, P是轮函数中线性变换矩阵。σ进行交换Feistel状态左半边与右半边的操作, 则ℱSP的对偶结构定义为。

令ɛSP为 SPN结构, 线性变换可逆矩阵为P, 则ɛSP的对偶结构定义为。

对于ℱSP结构, 零相关和不可能差分的等价性见下述定理。

定理11( [25, 定理1] ).

a→b是ℱSP的一条r轮不可能差分路线当且仅当它是的一条r轮零相关路线。

对ɛSP结构具有类似结论。

定理12( [25, 定理2] ).

a→b是ɛSP的一条r轮不可能差分路线当且仅当它是的一条r轮零相关路线。

当中的矩阵P是一个可逆矩阵时, 由于存在等式

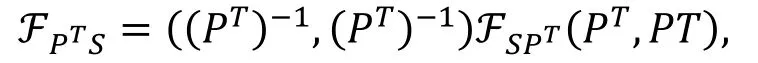
可以得到如下推论。

推论5( [25, 推论2] ).

令ℱSP为具有SP结构轮函数的Feistel结构, 如果轮函数中的线性矩阵P是可逆的, 则寻找ℱSP的零相关路线等价于寻找的不可能差分路线。

推论6( [25, 推论3] ).

令ℱSP为具有SP结构轮函数的Feistel结构, 如果轮函数中的线性矩阵P是可逆的, 且有P=PT, 则在不可能差分和零相关之间存在一一对应关系。对于SPN结构ɛSP, 如果PTP=E,a→b是一条不可能差分路线当且仅当它是一条零相关线性路线。

通过研究零相关与不可能差分区分器之间的关联, 在已知其中一类区分器的情况下, 我们可以利用该关联性判断是否存在与之类似的另一类区分器,并且在存在的情况下直接将等价区分器推导得出。在研究零相关与不可能差分关系的文献中, 许多新的区分器被提出来。另一方面这两种区分器在攻击方式上也不同, 我们可以从等价的区分器中选择更适合攻击的区分器进行算法攻击。

不过这些等价性也存在一些不足: 这些关联覆盖的结构还不够完整, 而且等价关系存在的条件比较苛刻。例如: 文献[24]中, 等价性建立在Z是置换的条件之下, 所以其无法用SMS4或MARS算法自己的结构解释零相关与不可能差分区分器的等价性,这就限制了等价关系的应用; 文献[25], 主要针对SP结构的Feistel算法和SPN算法。

5.2 零相关与积分攻击

积分区分器包括两类:

·在选择明文(或密文)满足一定条件下, 输出的某些比特异或和为0(称其为零和积分区分器)。

· 在选择明文(或密文)满足一定条件下, 输出的某些比特构成的数出现次数完全相等(称其为平衡积分区分器)。

零相关线性区分器主要与平衡积分区分器存在关联。

2012年的亚洲密码年会上, Bogdanov[13]等人给出了特定形式的零相关区分器与积分区分器之间的关系。与一般的积分区分器考虑输出某部分异或和的性质不同, 文献[13]中所考虑的积分区分器要求输出在某一空间内满足平衡特性。在给出具体关联之前, 我们根据文献[13]先给出一些定义。

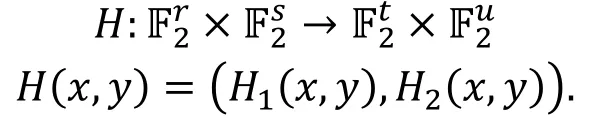
定义函数Tλ如下:

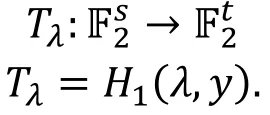
根据上述定义, 我们可以表示出平衡积分区分器和零相关线性区分器的数学表示形式。

·平衡积分区分器: 当x固定为常数, y遍历所有可能的取值, 输出的前t比特是平衡的(也就是每一个数出现的次数相等)表示为:

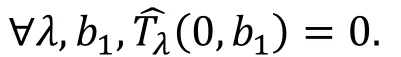
·零相关区分器: 当函数H的输入掩码为a=(a1,0),

输出掩码为b=(b1,0)时, a→b是零相关的表示为:

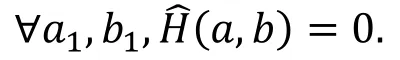
实际上, 上述零相关区分器是多维的, 表示只要a1、b1不同时为零的情况下, a→b是零相关的。

命题7( [13, 命题1] ).

若输入掩码a与输出掩码b相互独立, 则下面两条结论等价:

1. 对任意的a=(a1,0)和b=(b1,0)≠0, 线性逼近a·x+b·H(x)是零相关线性逼近;

2. 对任意的λ,Tλ是平衡的。

文献[13]指出: 积分区分器可以无条件的转换为一个零相关区分器, 而当零相关区分器转化为积分区分器是要求零相关区分器的输入掩码与输出掩码相互独立。这一等价性非常有趣, 因为零相关分析和积分分析不管是在区分器的构造上还是密钥恢复攻击上看起来都十分不同。首先, 零相关分析是已知明文攻击, 而积分攻击是选择明文攻击。其次, 在零相关区分器前面加轮数并不会使攻击的数据复杂度增加, 但在积分区分器前面加轮数一般会导致所需的选择明文的个数增加, 这是因为区分器的头部要求某些比特为固定值, 为满足这一条件就需要以牺牲数据复杂度为代价。除此之外, 满足平衡特性的积分区分器一般可以通过将平衡特性放宽为零和特性(或使得最后输出某部分的函数不具有最高的代数次数)而使区分器加长一轮, 但对于零相关区分器, 还没有发现这种可以加长一轮的性质。

上面的零相关区分器与积分区分器相互推导的条件限制着命题7的一般性应用, 观察命题7中的条件, 要求输入输出掩码是相互独立的, 而且掩码是由非零任意值与 0级联而成, 这就出现了两种无法直接应用命题7的情况:

1. 输入掩码中要求某些比特掩码值必须为1时的零相关路线(在 ARX结构的算法或是比特级操作的算法会出现此种路线)。

2. 输入输出掩码不独立, 例如要求a1=b1或a1≠b1条件下的零相关路线。

对于第 1种情况, 温隆和王美琴[33]对其作了进一步研究, 给出的结果主要是从零相关路线推导积分路线, 由于在输入掩码中含有必须为1的部分, 其将算法H′的输入分割成了三部分, 表示如下:

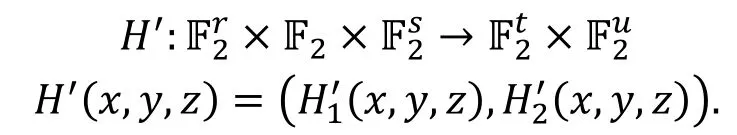
命题8( [33, 命题2] ).

对于第 2种情况, 输入输出掩码不独立的情况下, 从零相关路线推导积分区分器的问题由孙兵等人在文献[25]中得到解决。

推论7( [25, 推论4] ).

从推论 7可以看出, 只要零相关线性路线的输入掩码构成一个子空间, 就可以从中导出一条积分路线, 进一步, 输入掩码构成子空间这一条件也可以去掉, 得出如下定理。

定理13( [25, 定理3] ).

分组密码算法的任一非平凡的零相关线性壳总是可以推导出一条积分路线。

定理13成立主要是因为: 对任一条零相关线性路线a,*0,a+就可以构成一个子空间, 再根据推论 7就得到了定理13的结论。

零相关分析与积分攻击之间的关联性有助于我们利用这种关联性构造新的区分器, 并且根据攻击方式的不同, 我们可以从等价区分器中选择更适合攻击的区分器。现有关联性之间的不足在于: 目前的结果虽然可以无条件的将零相关区分器转化为积分区分器, 但是是在减少使用的零相关路线条数的情况下实现的, 这可能会导致找到的积分区分器需要较大的数据量, 影响了区分器攻击的有效性。例如对于ARX结构的算法, 零相关路线的掩码中会存在必须为1的部分, 无法构成大的子空间, 如何将更多的零相关路线应用到应用的积分区分器的构造中值得进一步思考。另一方面, 从积分区分器到零相关的转化目前为止局限于平衡积分区分器方面, 是否可以从零和区分器构造零相关路线还未被解决。

5.3 不可能差分与积分攻击

孙兵等人在文献[25]中讨论了不可能差分区分器和积分区分器之间的关联, 这些结果主要是从上面零相关路线与不可能差分路线之间的关联以及零相关路线与积分路线之间的关联推导而出。

由于ɛ⊥的一条零相关线性壳总可以导出ɛ⊥的一条积分路线, 而ɛ⊥的零相关线性壳可以从ɛ的不可能差分路线导出, 从而得出下述定理。

定理14( [25, 定理4] ).

令ɛ∈*ℱSP,ɛSP+, 则ɛ的一条不可能差分路线总是可导出ɛ⊥的一条积分路线。

当A1、A2为线性变换, ɛ⊥=A2ɛA1时, 可以得到不可能差分路线与积分路线的直接关联:

推论8( [25, 推论5] ).

令ℱSP为轮函数为SP结构的Feistel结构算法, 且轮函数中线性变换为P。如果P是可逆的, 且对任意的, 存在对这t个元素的置换π,使得:

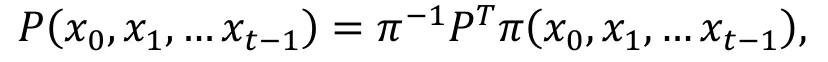
则对于ℱSP, 一条不可能差分路线可以导出一条积分路线。

对于 SPN结构的算法, 也存在着不可能差分与积分路线之间的直接关联。

推论9( [25, 推论6] ).

令ɛSP为 SPN结构的算法, 线性层表示为P, 如果PTP=diag(Z1,Z2,…Zt), 其中, 则对于ɛSP, 一条不可能差分路线可以导出一条积分路线。

如果线性层P是一个比特置换矩阵, 则一定满足PTP=E是对角矩阵, 则得出如下结论。

推论10( [25, 推论7] ).

对任意的以比特置换为线性混乱层的SPN结构的算法, 一条r轮的不可能差分路线可以导出一条r轮积分路线。

目前为止, 不可能差分与积分攻击之间的关联主要是从不可能差分与零相关以及积分与零相关之间的关联性推导而出, 这两者之间是否存在其他的、两者独有的关联值得进一步思考。

6 不可能差分与截断差分分析

李雷波等人[28]受到不可能差分的启发, 通过将截断不可能差分中间相错的关键步骤以一定的概率转为中间相遇(图 4), 同时保证差分Γ0→Γ2成立的概率足够大(可以与随机置换区分), 这样就完成了不可能差分到截断差分的转换。得益于截断不可能差分的自动化搜索方法, 这一关系的发现将可能有助于促进截断差分搜索的自动化。作者也将该方法应用于CLEFIA[34]和Camellia[35]的攻击中, 并得到了较好的结果。

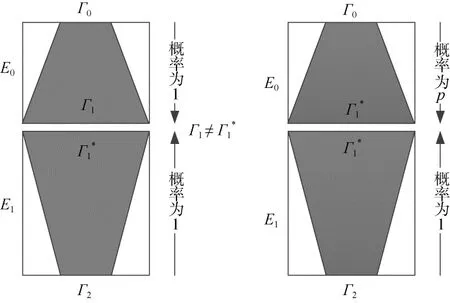
图5 不可能差分转为截断差分

对于随机置换而言, 截断差分Γ0→Γ2成立的概率为, 其中n为分组长度。当同样的截断差分对于算法的概率时, 则这一截断差分可以当做区分器来恢复密钥。文献[28]假设E为Markov算法[29],即差分特征的概率用每一轮的概率相乘得到。

想要计算Pr*Γ0→Γ2+, 由

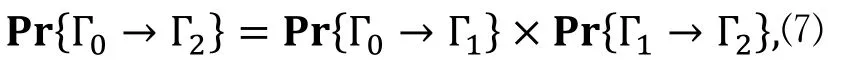
已知Pr*Γ2→Γ1+=1, 为计算Pr*Γ1→Γ2+, 作者引入了下面的假设。

假设1( [28, 假设1] ).

对于截断差分Γin→Γout, 若E为 Markov算法, a∈Γin,b∈Γout时, 我们有

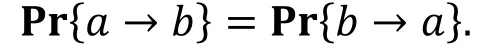
利用假设1, 我们可以计算Pr*Γ1→Γ2+。

命题9( [28, 命题1] ).

假设截断差分Γ2→Γ1成立的概率为 1, 则在假设1之下, 截断差分Γ1→Γ2成立的概率为

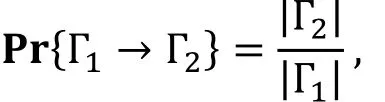
其中|Γ2|≤|Γ1|。

根据命题9, 当我们将不可能差分转为截断差分时, 截断差分的概率可以用下面命题计算。

命题10( [28, 命题3] ).

对于分组密码E=E1∘E0, 假设有两段高概率的截断差分, 即Pr*Γ0→Γ1+=p,Pr*Γ2→Γ1+=q。则截断差分Γ0→Γ2的概率大于。

利用中间相遇的方法找到的截断差分也可以用上面的命题计算概率, 但由于不可能差分的寻找可以得益于自动化搜索的方法, 所以这一命题将可能有助于截断差分搜索的自动化。这样的特性在许多分组密码中存在, 特别是 Fesitel结构的密码, 如CLEFIA、Camellia等。

7 小结

本文中, 我们简要介绍了一些已有的统计分析方法, 并总结了已有的统计分析方法之间的关联性。这些关联性的建立一方面有助于我们对已知的分组密码分析方法进行分类, 另一方面这些关联性可能会给出分组密码安全性的补充信息。除此之外, 研究统计分析方法之间的关系, 也有助于我们用较为完善的理论体系丰富和发展密码体系中较为薄弱的环节。

纵观所有已经提出的关联性, 研究这些关联性的价值有以下几方面:

1. 通过研究两种统计分析方法的关联性, 在已知其中一类区分器D1的情况下, 我们可以利用该关联性直接导出与之相等价的另一类区分器D2。但直接推导区分器D2可能较为困难, 利用等价性可以便于我们发现更长轮数的区分器。

2. 两种具有等价关系的统计分析方法在攻击方式上可能存在不同(一种是已知明文攻击, 另一种是选择明文攻击), 我们可以从等价的区分器中选择更适合攻击的区分器进行算法攻击。

3. 研究统计分析方法之间的关系, 也有助于我们用较为完善的理论体系丰富和发展密码体系中较为薄弱的环节。例如: 通过多维线性和统计饱和度攻击在本质上的统一性, 我们可以确切的衡量统计饱和度攻击中使用的数据量。

当然, 现存的各种统计分析方法之间的关联性也存在一些不足:

1. 一些现有的关联性完全由数学公式推导而得,并不依赖于底层算法的结构, 这种等价性虽具有一般性, 但缺少实用性。

2. 现有的关联性覆盖的结构还不够完整, 而且等价关系存在的条件也比较苛刻, 这些缺陷也限制了这些等价性的应用。

有些关联性(如: 不可能差分与积分攻击之间的关联性)是从一些现有的关联性推导而来, 而所涉及的统计分析方法之间是否存在其他的、二者独有的关联值得进一步思考。

[1] E. Biham, and A Shamir, "Differential Cryptanalysis of DES-like Cryptosystems,"Journal of Cryptology, vol. 4, no. 1, pp. 3-72, 1991.

[2] L. R. Knudsen, "Truncated and High Order Differentials," inFast Software Encryption, vol. 1008,pp.196-211, 1995.

[3] L. R. Knudsen, "DEAL - A 128-bit Block Cipher".Technical report, DEPARTMENT OF INFORMATION, University of Bergen, 1998.

[4] E. Biham, A. Biryukov, and A. Shamir, "Cryptanalysis of Skipjack Reduced to 31 Rounds Using Impossible Differential," inAdvances in Cryptology – EUROCRYPT 1999 (EUROCRYPT’99), pp. 12-23, 1999.

[5] D. Wagner, "The Boomerang Attack" inFast Software Encryption -FSE 1999, pp. 156-170, 1999.

[6] E. Biham, O. Dunkelman, and N. Keller, "The Rectangle Attack -Rectangling the Serpent," inAdvances in Cryptology –EUROCRYPT 2001 (EUROCRYPT’01), pp. 340-357, 2001.

[7] J. Kim, S. Hong, J. Sung, S. Lee, and J. Jim, "Impossible Differential Cryptanalysis for Block Cipher Structures," inIndocrypt 2003, pp. 82-96, 2003.

[8] Y. Luo, X. Lai, Z. Wu, and G. Gong, "A Unified Method for Finding Impossible Differentials of Block Cipher Structures," inInformation Sciences, vol. 263, no. 1, pp. 211-220, 2014.

[9] M. Matsui, "Linear Cryptanalysis Method for DES Cipher," inAdvances in Cryptology – EUROCRYPT 1993 (EUROCRYPT’93), pp. 386-397, 1994.

[10] M. Matsui, "The First Experimental Cryptanalysis of the Data Encryption Standard," inAdvances in Cryptology - CRYPTO 1994 (CRYPTO'94), pp. 1-11, 1994.

[11] J. Burton, S. Kaliski, and M. J. B. Robshaw, "Linear Cryptanalysis Using Multiple Approximations," inAdvances in Cryptology -CRYPTO 1994 (CRYPTO'94), pp. 26-39, 1994.

[12] M. Hermelin, J. Y. Cho, and K. Nyberg, "Multidimensional Extension of Matsui's Algorithm 2," inFSE 2009, vol. 5665, pp. 209-227, 2009.

[13] A. Bogdanov, and V. Rijmen, "Linear Hulls with Correlation Zero and Linear Cryptanalysis of Block Ciphers," inDesigns, Codes and Cryptography, vol. 70, no. 3, pp. 369-383, 2014.

[14] A. Bogdanov, and M. Wang, "Zero Correlation Linear Cryptanalysis with Reduced Data Complexity," inFast Software Encryption - FSE 2012, pp. 29-48, 2012.

[15] A. Bogdanov, G. Lender, K. Nyberg, and M. Wang, "Integral and Multidimensional Linear Distinguishers with Correlation Zero," inAdvances in Cryptology - ASIACRYPT 2012, pp. 244-261, 2012.

[16] S. Murphy, "The Independence of Linear Approximation in Symmetric Cryptology,"IEEE Transactions on Information Theory, vol. 52, no. 12, pp. 5510-5518, 2006.

[17] J. Daemen, L. Knudsen, and V. Rijmen, "The Block Cipher SQUARE," inFast Software Encryption - FSE 1997, pp. 149-165, 1997.

[18] L. R. Knudsen, and D. Wagner, "Integral Cryptanalysis," inFast Software Encryption - FSE 2002, pp. 112-127, 2002.

[19] B. Collard, and F. X. Standaert, "A Statistical Saturation Attack against the Block Cipher PRESENT," inCT-RSA 2009, vol. 5473, pp. 195-210, 2009.

[20] F. Chabaud, and S. Vandenay, "Links between Differential and Linear Cryptanalysis," inEUROCRYPT 1994 (EUROCRYPT’94), pp. 356-365, 1994.

[21] C. Blondeau, K. Nyberg, "New Links between Differential and Linear Cryptanalysis," inEUROCRYPT 2013 (EUROCRYPT’13), pp. 388-404, 2013.

[22] C. Blondeau, K. Nyberg, "Links between Truncated Differential and Multidimensional Linear Properties of Block Ciphers and Underlying Attack Complexities," inEUROCRYPT 2014 (EUROCRYPT’14), pp. 165-182, 2014.

[23] A. A. Selçuk, "On Probability of Success in Linear and Differential Cryptanalysis,"Journal of Cryptology, vol. 21, no. 1, pp. 131-147, 2008.

[24] C. Blondeau, A. Bogdanov, M. Wang, "On the (In) Equivalence of Impossible Differential and Zero Correlation Distinguishers for Feistel- and Skipjack-type Ciphers," inACNS 2014, pp. 271-288, 2014.

[25] B. Sun, Z. Liu, V. Rijmen, R. Li, L. Cheng, Q. Wang, …, and C. Li, "Links among Impossible Differential, Integral and Zero Correlation Linear Cryptanalysis," inCRYPTO 2015.

[26] A. Bogdanov, L. R. Knudsen, G. Leander, C. Paar, A. Poschmann, M. J. Robshaw, …, C. Vikkielsoe, "PRESENT: An Ultra-lightweight Block Cipher,"Springer Berlin Heidelberg Press, 2007.

[27] G. Lender, "On Linear Hulls, Statistical Saturation Attacks, Present and a Cryptanalysis of PUFFIN," EUROCRYPT 2011 (EUROCRYPT‘11), pp. 303-322, 2011.

[28] L. Li, K. Jia, X. Wang, and X. Dong, "Meet-in-the-Middle Techniques for Truncated Differential and Its Applications to CLEFIA and Camellia," inFast Software Encryption, pp. 48-70, 2015.

[29] X. Lai, and J. L. Massey, "Markov Ciphers and Differential Cryptanalysis," inEUROCRYPT 1991 (EUROCRYPT’91), pp. 17-38, 1991.

[30] K. Nyberg, "Linear Approximations of Block Ciphers," inAdvances in Cryptology - EUROCRYPT 1994 (EUROCRYPT’94), pp.439-444, 1994.

[31] J. Y. Cho, "Linear Cryptanalysis of Reduced-round PRESENT," inTopics in Cryptology - CT - RSA 2010, pp. 302-317, 2010.

[32] M. Z‗aba, H. Raddum, M. Henricksen, and E. Dawson, "Bit-pattern Based Integral Attack," inFast Software Encryption -FSE 2008, pp. 363-381, 2008.

[33] L. Wen, and M. Wang, "Integral Zero-Correlation Distinguisher for ARX Block Cipher, with Application to SHACAL-2," inInformation Security and Privacy, pp. 454-461, 2014.

[34] T. Shirai, K. Shibutani, T. Akishita, S. Moriai, and T. Iwata, "The 128-bit Block Cipher CLEFIA," in Fast Software Encryption –FSE2007, pp. 181-195, 2007.

[35] A. Kato, S. Moriai, M. Kanda, "The Camellia Cipher Algorithm and its use with IPSec," https://tools.ietf.org/html/rfc4312, 2005.

王美琴 于2007年在山东大学信息安全专业获得博士学位。现任山东大学密码技术与信息安全教育部重点实验室副主任。研究领域为对称密码分析与设计。研究兴趣包括: 零相关线性分析、积分攻击等。

Email: mqwang@sdu.edu.cn

孙玲 于2014年在山东大学大学数学与应用数学专业获得理学学士学位。现在山东大学信息安全专业攻读硕士学位。研究领域为分组密码的分析与设计。研究兴趣包括: 差分分析与线性分析等。

Email: lingsun@mail.sdu.edu.cn

陈怀风 于2012年在山东大学信息安全专业获得理学学士学位。研究领域为分组密码的分析与设计。研究兴趣包括: 差分分析和线性分析等。

Email: hfchen@mail.sdu.edu.cn

刘瑜 于2008年在山东大学信息安全专业获得硕士学位。现在山东大学信息安全专业攻读博士学位。研究领域为分组密码。研究兴趣包括: 差分分析和线性分析等。

Email: liuyu01@mail.sdu.edu.cn

A Brief Analysis of Links between Different Types of Cryptanalytic Methods for Block Cipher

WANG Meiqin, SUN Ling, CHEN Huaifeng, LIU Yu
Key Lab of Cryptologic Technology and Information Security Ministry of Education, Shandong University, Jinan 250100, China

Many cryptanalytic methods have gradually appeared since the successive foundation of linear cryptanalysis and differential cryptanalysis. Various cryptanalytic methods usually use the nonuniformity of the data extracted from the ciphers to get the information of the secret key. Some similar phenomena can be found when using these cryptanalytic methods to analyze the security of block ciphers. For example, the number of rounds covered by certain two distinguishers is always the same, and there exist some mathematical links between certain two statistical cryptanalysis methods. So, people are gradually shifting their concern to discover the links between various existing cryptanalytic methods while proposing new cryptanalytic methods. Despite the formal differences lie in the management and the cryptanalysis, there exist some links between many cryptanalytic methods which may look different after carefully research. Discovering this kind of links is necessary not only from the point of theoretical but also from the perspective of estimating the security of block ciphers. Many links between cryptanalytic methods have gradually been built in recent years. The establishing of these links, on the one hand, can help us classify existing cryptanalysis methods of block ciphers. On the other hand, these may give some supplement information of the security of block ciphers. In this paper, we briefly introduce some existing cryptanalytic methods and summarize the links between existing cryptanalytic methods.

block ciphers; cryptanalytic methods; links

TP309.7

王美琴, 博士, 教授, Email: mqwang@sdu.edu.cn。

本课题得到 973计划(No. 2013CB834205); 国家自然科学基金(No. 61133013 和 No. 61572293); 新世纪优秀人才支持计划(No. NCET-13-0350)资助。

2015-12-01；修改日期：2015-12-22；定稿日期：2016-01-08