R.Pakniat, M.K.Tavassoly, and M.H.Zandi

1Faculty of Physics,Shahid Bahonar University of Kerman,Kerman,Iran

2Atomic and Molecular Group,Faculty of Physics,Yazd University,Yazd,Iran

3Photonic Research Group,Engineering Research Center,Yazd University,Yazd,Iran

4The Laboratory of Quantum Information Processing,Yazd University,Yazd,Iran

1 Introduction

Entanglement and superposition of states are known as two cornerstones of the quantum information theory.The Jaynes–Cummings model(JCM)[1−2]as a full quantum mechanical approach to the interaction between a two-level atom and a single-mode quantized field is a simple method for the construction of entangled state.After introducing the JCM,a great deal of efforts have been performed in the generalization of this model.[3−4]For example,the multi-mode field is employed instead of single-mode field,[5−8]intensity-dependent coupling[9−10]and time-dependent coupling[11]instead of constant atom-field coupling.Among them,one of the generalizations is considering different con figurations of three-level atoms instead of two-level atoms.[12]In particular,the interaction of a Ξ-type three-level atom with a single-mode field has been studied numerously[13−15]and the exact form of probability amplitudes of the state of such an atom- field system is discussed.

On the other hand,entropy as a measure of information in a quantum system has been studied in different forms.[16]In quantum physics,for a system identified with density matrixthe von Neumann entropy is defined as S()=−Tr(ρˆlnρˆ).[16]This entropy can be written versuPs the eigenvalues of the density matrix(ρm)as S(ρ)=mρmlnρm.This relation is similar to(classical)Shannon entropy for a probability distribution which is defined asIn a similar manner,the Shannon entropy for a continuous probability distribution with the density distribution function P(ξ)is expressed as[17]

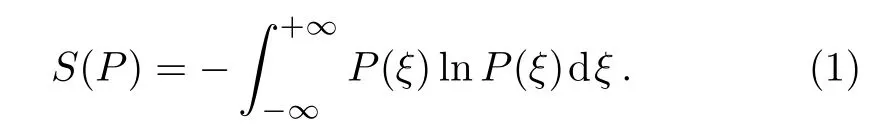
Accordingly,for the continuous observables like position and momentum which correspond to the wave functions ψ(x)and φ(p),respectively,Eq.(1)can be rewritten as

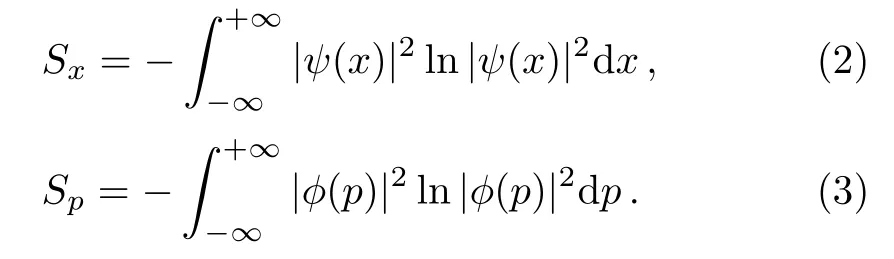
In past decades,great interest has been paid to determine the non-commuting observables in quantum systems and then to the formulation of uncertainty relations for such.[18−20]In this regard,numerous efforts for determination of the lower bound of entropies summation for two non-commutating observablesˆx andˆp are performed.In the meantime,Beckner,Bialynicki–Birola and Mycielsky(BBM)have calculated this limitation as 1+lnπ,[21−22]and expressed that the summation of entropies satisfies the following BBM inequality

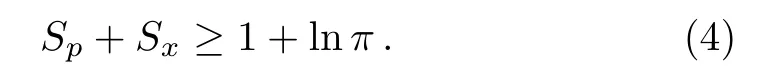
It is claimed that,this inequality is indeed a stronger version of the Heisenberg uncertainty relation and is satisfied for two non-commutating Hermitian operators[18]in all physical systems.More exact review on BBM inequality is given by Dodonov and Manko in Ref.[23].So far,the position and momentum entropies are calculated for different potentials.For instance,the probability representation of quantum and classical statistical mechanics is discussed in Ref.[24]and then entropic uncertainty relations and inequalities for spin tomograms are reviewed.In Ref.[25]the Shannon entropies of position and momentum for the stationary states of the harmonic oscillator are calculated as a function of quantum number n(or equivalently the energy of the oscillator)and the corresponding entropic uncertainty relations are determined,too.The authors also studied the time evolution of the position and momentum entropies of the non-stationary states corresponding to a few well-known classes of states such as coherent states,a typical squeezed vacuum and Schr¨odinger cat states.Also,these entropies are calculated for the ground state of P¨oschl-Teller potential analytically and,for its excited state numerically and then the validity of BBM inequality is con firmed.[26]In addition,in the case of Morse potential,these entropies are numerically obtained by regarding different parameters and the validity of BBM inequality is also con firmed.[27]Recently,the position and momentum entropies for the eigenstates of isotonic oscillator are calculated by one of us.[28]In Ref.[28],the validity of BBM inequality is established and it is observed that for some eigenstates,the entropy squeezing occurs in position space,denoting the non-classicality nature of the considered eigenstates.More recently,considering the eigenstates of a confined quantum system,i.e.,infinite circular well,the corresponding Shannon information entropies are evaluated and the variation of the values of position(radial)and momentum entropies versus radius of the well are investigated.[29]

The latter-mentioned studies which have been pointed out,contain the investigation of position and momentum entropies and the validity of BBM inequality(Eqs.(2)and(3))for a few of the well-known stationary states§§We should emphasize that only in Ref.[25]the authors took a look at a few classes of,as they claimed,nonstationary states;however,our considered states are rather different(they are actually dynamical entangled states).In our opinion,studying the time evolution of Shannon entropy of two classes of nonstationary states has been performed in the present paper in an appropriate manner.corresponding to some given potentials,with no entanglement between the considered eigenstates.However,the aim of the present study is to investigate the position and momentum information entropies for two classes of atom-field entangled state which are extracted from JCM and one of its generalizations.These states,in addition to have the entanglement property,are also time-dependent.Therefore,the obtained entropies vary with time and consequently they are not stationary as those which are discussed previously in Refs.[21–22,25–28]It is also shown that for particular values of evolved parameters of the whole atom- field system,the entropy squeezing(as a nonclasicallity indicator)may be observed.Also,the confirmation of the BBM inequality for the time-dependent entangled states is investigated as time goes on.To achieve these purposes,we consider two different systems.The first one which we will consider is the entangled state due to the interaction of a two-level atom with a single-mode quantized field[30]and the second,is the entangled state extracted from the interaction of a Ξ-type three-level atom with a single-mode field.[13−15]

The rest of the paper is as follows:In Sec.2,two different atom- field configurations are reviewed and the corresponding Shannon position and momentum entropies are then introduced.In Sec.3,the numerical results are presented and finally in Sec.4 we give a summary and conclusion.

2 Dynamics of Entropy in Position and Momentum Spaces for the Atom-Field Entangled States

In this section,at first we briefly review on two different types of atoms which interact with a single-mode quantized field and the exact form of the corresponding probability amplitudes of the atom- field entangled state will be given,distinctly. Then,we evaluate the timedependent Shannon entropy in position and momentum spaces as well as the BBM inequality associated with each state vector,separately.

2.1 Introducing Two Classes of Atom-Field Entangled State

For a two-level atom which interacts with a singlemode quantized field in a cavity,the Hamiltonian in the interaction picture reads aswhere g is the atom- field coupling coefficient,∆=ω−ω0is the detuning between the frequencies of the field(ω)and the atomic transition(ω0)andare respectively the atomic raising and lowering operators.Also(†)is the annihilation(creation)operator of the field.If the two-level atom is initially prepared in its excited state|ei,the state vector of the above-mentioned system at time t can be expressed as[30]

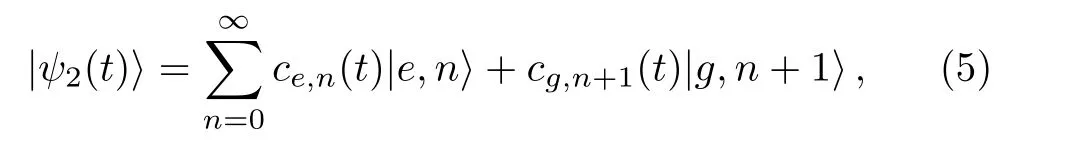
with the probability amplitudes

with Ωnas the Rabi frequency and cn(0)as the expansion coefficient of the initial field.Notice that the subscript 2 in|ψ2(t)i refers to the two-level atom.

Similarly,for a Ξ-type three-level atom with the ground state|gi and the excited states|fi and|ei,the allowed transitions are considered only|ei←→ |fi and|fi←→|gi.Assuming that such an atom interacts with a single-mode quantized field in a cavity,the corresponding Hamiltonian in the interaction picture reads aswhereare the atomic raising operators,andare the atomic lowering operators;also g1and g2are the atom-field coupling coefficients.Here,δ= Ω − (ωe− ωf)=(ωf−ωg)−Ω,where Ω is the cavity- field frequency and ωe,ωfand ωgare the frequencies associated with the atomic levels|ei,|fi and|gi,respectively.The state vector of the above-mentioned system at any time t can be expressed as below

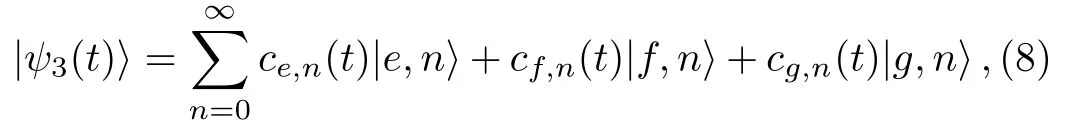
where the subscript 3 in|ψ3(t)i refers to the three-level atom.Assuming cn(0)as the expansion coefficient of the initial field and considering the initial state of the atom as|ψ0i=ce|ei+cf|fi+cg|gi,the time-dependent coefficients in Eq.(8)have been obtained as[13−15]

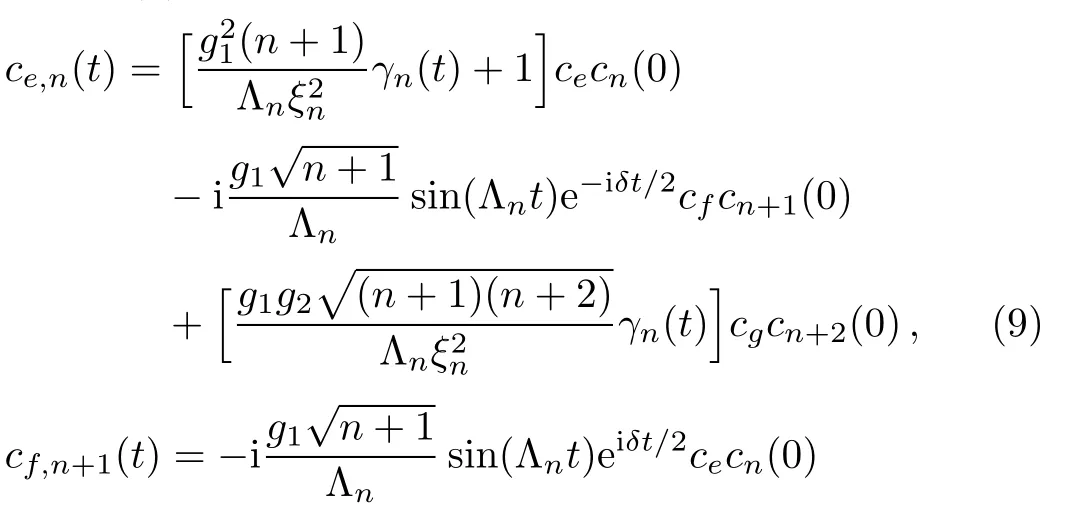
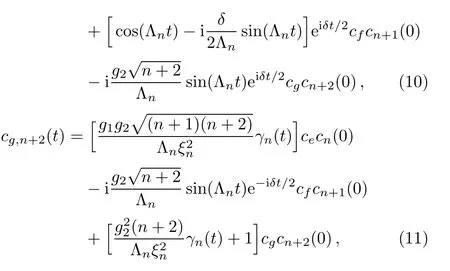
whereis the Rabi frequency withand

It should be noticed that,in relations(9)–(11)it is assumed that the field is initially in a coherent state,that is,

2.2 Time-Dependent Shannon Entropy in Position and Momentum spaces

As is seen,the introduced states in Eqs.(5)and(8)are clearly time-dependent and entangled.Our aim in this paper is to investigate the dynamical behavior of position and momentum entropies for the mentioned states.To achieve this goal,by using Eqs.(5)and(8)the probability densities of these states in terms of position and time are explicitly obtained as

where un(x)with n=0,1,2,...which are the eigenfunctions of harmonic oscillator in position space has been de fi ned as[31]

with Hnas the Hermit polynomials and

On the other hand,using Eq.(14)one may obtain the eigenfunctions of the Hamiltonian of harmonic oscillator in momentum space as

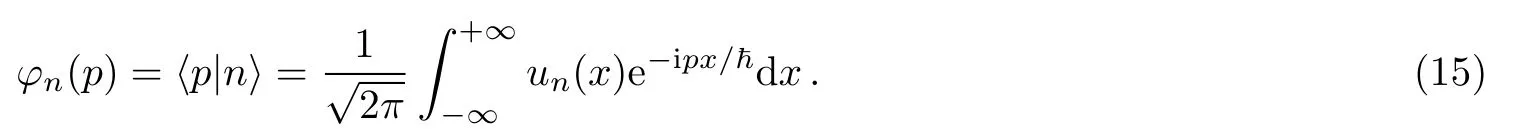
Therefore,in a similar manner to Eqs.(12)and(13),the probability densities of the entangled states|ψ2(t)i and|ψ3(t)i in term of momentum and time may be expressed as

According to Eqs.(2)and(3),the time-dependent Shannon entropy corresponding to position and momentum spaces can be rewritten respectively as

where the densities of entropies are respectively defined as follow:

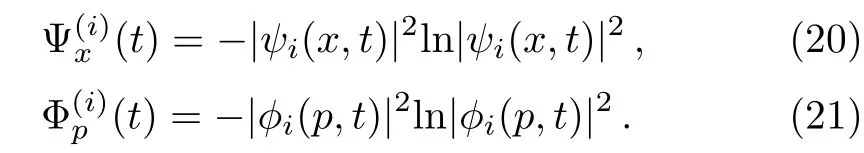
Thus,considering the above discussion we can evaluate Sx(t)and Sp(t)as well as the BBM inequality for the above-mentioned two classes of entangled states.

3 Numerical Results

In this section we aim to show the results of our study,numerically.The constant parameters in the whole of the paper are chosen as m=~=1,∆=g,ω =10g.

3.1 Two-Level Atom

In Fig.1 the time evolution of the entropy density of the entangled state|ψ2(t)i in Eq.(5)is depicted in position and momentum representations.In fact,more localization of the wave function leads to lower values of entropy.[22]In order to analyze our numerical results,two different values of the initial intensity of the field are considered,i.e.,|α|2=1,10.In Fig.1(a),the entropy density in position space is plotted versus the scaled time gt for|α|2=1.As is seen from this plot,in a given time significant oscillations around the origin occur and by enough increase and decrease of x(|x|≃1.4),the value of entropy density vanishes symmetrically.In the regions far from the origin(|x|>1.12)no critical changes for position entropy density can be observed.In Fig.1(b),the entropy density in position space is plotted against the scaled time and position,by considering higher light intensity,|α|2=10.It is seen that the diagram has significant values around the origin of x,and by going far enough from the origin(around|x|≃1.89),the value of entropy density vanishes.In comparison with Fig.1(a)the value of entropy density vanishes in greater value of position(|x|≃2.16)and the strong oscillations around x=0 is no longer seen.In Fig.1(c)the entropy density diagram for the entangled state|ψ2(t)i is depicted in momentum space for|α|2=1.As is deduced from this figure,the entropy density curve possesses some variations around the origin of p and by going far enough from the origin(|p|≃12.5)the value of momentum entropy density tends to zero.The dynamics of entropy density in momentum space with|α|2=10 is plotted in Fig.1(d).A simple comparison between Figs.1(c)and 1(d)shows that while the maxima of momentum entropy in low intensity is nearly at the origin,in the higher intensity it has a local minimum at the origin and then gains its maxima symmetrically around|p|≃13.25.In addition,as is observed the momentum entropy density vanishes at greater values of p(|p|=21.25)in|α|2=10 with respect to the case with|α|2=1.

Fig.1 Dynamical behavior of the entropy density in(a),(b):position and(c),(d):momentum spaces versus scaled time gt for state vector|ψ2(t)i in Eq.(5).

In this stage we want to discuss about the entropy squeezing in position space as well as the BBM inequality(Eq.(4))upon the relations(18)and(19).In Figs.2(a)and 2(b)we have plotted the dynamics of Shannon entropy in position space in terms of the scaled time gt.Also,in Figs.2(c)and 2(d)the sum of the entropies in position and momentum spaces are depicted versus the scaled time.

Our numerical results show that for the case with|α|2=1(Fig.2(a)),the value of Shannon entropy in position space is less than(1+lnπ)/2=1.0723,i.e.,the entropy squeezing occurs in position space.But,in the case of|α|2=10(Fig.2(b))no squeezing is observed.Our numerical results,not shown here,illustrate that in momentum space there is no entropy squeezing.On the other hand,the BBM inequality,as a more strong version of the Heisenberg uncertainty relation,is con firmed for the entangled states of our considered atom- field system.This fact is clear from Figs.2(c)and 2(d),which show the time behavior of S(2)x+S(2)pfor state vector(5);recalling the value of 1+lnπ=2.1447,it is manifestly seen that in all instants of time the BBM inequality is satisfied.

Fig.2 Dynamical behavior of(a),(b):S(2)x and(c),(d):S(2)x +S(2)p versus scaled time gt for state vector|ψ2(t)i in Eq.(5).

3.2 Three-Level Atom

First of all it should be stated that,in our numerical results in this subsection the coupling coefficients for the three-level atom- field state|ψ3(t)i in Eq.(8)are assumed to be equal,i.e.,g1√=g2=g and the atomic coefficients ce=cf=cg=determine the initial atomic state.In Fig.3 the dynamics of the entropy density of the entangled atom- field state(8)in position and momentum spaces is plotted versus the scaled time gt.In Fig.3(a)(with|α|2=1)the strong oscillations are seen around x=0 so that these oscillations are further vanished by increasing the value of x in both directions.Altogether,it is seen that in a fixed given position around x=0 remarkable oscillations occur in time,but by exceeding the value|x|up to nearly 1 no changes are seen in the time behavior of the position entropy density.Also,in Fig.3(b),the entropy density in position space with|α|2=10 is plotted.It is clear that after an approximately monotonic behavior of this quantity around the origin of position,the curve quickly tends to zero.The dynamics of the entropy density of the entangled atom- field state(8)in momentum space is depicted in the three-dimensional Figs.3(c)and 3(d)versus the scaled time and momentum p.According to these diagrams,the oscillatory and symmetric variations are observed around p=0,however,they vanish by increasing the value of p in both directions.Comparing the numerical results for the state vectors|ψ2(t)i,|ψ3(t)i in Figs.1 and 3 it is understood that they qualitatively exhibit the same behavior.Altogether,a rigorous look at these two sets of plots shows that the values of the evolved quantity vary differently particularly around the origin of momentum.

In Fig.4 the time behavior of Shannon entropy in position space and the sum+for the state|ψ3(t)i are presented.It is again observable that,like Fig.2,for the case of|α|2=1(Fig.4(a))the maximum value of Shannon entropy in position space does not exceed(1+lnπ)/2 in all instants of time,i.e.,the entropy squeezing occurs.But,with|α|2=10(Fig.4(b))no entropy squeezing may be observed.

Fig.3 Dynamical behavior of the entropy density in(a),(b):position and(c),(d):momentum spaces versus scaled time gt for state vector|ψ3(t)i in Eq.(8).

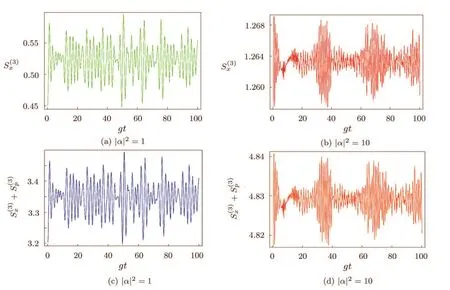
Fig.4 Dynamical behavior of(a),(b):and(c),(d):+versus scaled time gt for state vector|ψ3(t)i in Eq.(8).

In Figs.4(c)and 4(d)we have examined the validity of the BBM inequality(Eq.(4))for the state vector|ψ3(t)i.It is clear that the oscillatory curve is more than the limit 1+lnπ at all times and so our aim is satisfied.

4 Summary and conclusion

In this paper the dynamical behaviour of(Shannon)entropy in position and momentum spaces is calculated for the time-dependent entangled atom- field state vector which have been previously deduced using the JCM.Two different types of atoms,i.e.,two-level and ladder configured three-level atoms are employed for our purpose.These states in addition to possessing the entanglement property,are time-dependent,i.e.,they are both non-stationary state(unlike the previous considered states which are mainly stationary.[21−22,25−28])Therefore,the variation of entropy densities in position and momentum spaces are plotted versus the scaled time as well as the coordinates x or p for the two classes of atom- field states.The entropic densities are approximately symmetric around x,p=0,and after some variations around the origin,they vanish at some intermediate values of|x|,|p|.This zero limit occurs sooner for the x representation.On the other hand,we have shown that in particular cases of low initial field intensity(as we illustrated for|α|2=1|),entropy squeezing(as a non-classicality sign)occurs in position space.Therefore,the(Shannon)entropy densities and entropy squeezing can be managed by tuning the initial intensity of the field(which is discussed here)and also other evolved parameters of the whole system.Notice that laser behaves like coherent states far from the threshold.[30]Also,the obtained results con firm the BBM inequality in both system states,which is a stronger version of the Heisenberg uncertainty relation.

References

[1]E.T.Jaynes and F.W.Cummings,Proc.IEEE 51(1963)89.

[2]B.W.Shore and P.L.Knight,J.Mod.Opt.40(1993)1195.

[3]R.N.Daneshmand and M.K.Tavassoly,Laser Phys.25(2015)055203.

[4]E.Solano,G.S.Agarwal,and H.Walther,Phys.Rev.Lett.90(2003)027903.

[5]M.S.Abdalla,M.Ahmed,and A.S.Obada,Physica A 170(1991)393.

[6]H.R.Baghshahi,M.K.Tavassoly,and M.J.Faghihi,Laser Phys.24(2014)125203.

[7]H.R.Baghshahi,M.K.Tavassoly,and M.J.Faghihi,Int.J.Theor.Phys.54(2014)2839.

[8]M.J.Faghihi,M.K.Tavassoly,and M.B.Harouni,Laser Phys.24(2014)045202.

[9]S.R.Miry and M.K.Tavassoly,Phys.Scr.85(2012)035404.

[10]H.R.Baghshahi,M.K.Tavassoly,and A.Behjat,Commun.Theor.Phys.62(2014)430.

[11]A.Joshi and S.Lawande,Phys.Rev.A 48(1993)2276.

[12]M.J.Faghihi,M.K.Tavassoly,and M.R.Hooshmandasl,J.Opt.Soc.Am.B 30(2013)1109.

[13]A.H.Toor and M.S.Zubairy,Phys.Rev.A 45(1992)4951.

[14]W.B.Cardoso,A.T.Avelar,B.Baseia,and N.G.de Almeida,J.Phys.B:At.Mol.Opt.Phys.42(2009)195507.

[15]W.Cardoso,A.Avelar,B.Baseia,et al.,Opt.Commun.284(2011)1086.

[16]S.Barnett,Quantum Information,Oxford University Press,New York(2009).

[17]C.E.Shannon,Bell Syst.Tech.J.27(1948)623.

[18]J.B.M.Uffink and J.Hilgevoord,Found.Phys.15(1985)925.

[19]M.D.Srinivas,Pramana 24(1985)673.

[20]H.Maassen and J.B.M.Uffink,Phys.Rev.Lett.60(1988)1103.

[21]I.Bia lynicki-Birula and J.Mycielski,Commun.Math.Phys.44(1975)129.

[22]W.Beckner,Ann.Math.102(1975)159.

[23]V.V.Dodonov and V.I.Manko,Invariants and Evolution of Non-Stationary Quantum Systems,M.A.Markov,Nova Science Publishers,Commack,NY(1989).

[24]M.A.Man’ko and V.I.Man’ko,AIP Conf.Proc.1334(2011)217.

[25]V.Majernik and T.Opatrn`y,J.Phys.A:Math.Gen.29(1996)2187.

[26]R.Atre,A.Kumar,N.Kumar,and P.K.Panigrahi,Phys.Rev.A 69(2004)052107.

[27]E.Aydiner,C.Orta,and R.Sever,Int.J.Mod.Phys.B 22(2008)231.

[28]A.Ghasemi,M.r.Hooshmandasl,and M.K.Tavassoly,Phys.Scr.84(2011)035007.

[29]X.D.Song,G.H.Sun,and S.H.Dong,Phys.Lett.A 379(2015)1402.

[30]M.O.Scully and M.S.Zubairy,Quantum Optics,Cambridge University Press,Cambridge(1997).

[31]J.J.Sakurai,Modern Quantum Mechanics,Addison-Wesley,Reading(1994).