刘　锋,郭似童,谭祥勇,康新梅

(重庆理工大学 数学与统计学院,重庆　400054)



响应变量缺失下部分线性单指标模型的序列相关性检验

刘锋,郭似童,谭祥勇,康新梅

(重庆理工大学 数学与统计学院,重庆400054)

摘要：研究了在响应变量随机缺失下的部分单指标模型的序列相关检验问题。首先采用借补的方法对缺失响应变量进行处理,再运用经验似然方法对残差部分进行序列相关性检验,构造了经验似然比统计量，并证得其为渐近分布。数值模拟结果表明：该检验方法具有较为理想的检验功效。

关键词：部分单指标模型；缺失数据；随机缺失；经验似然；序列相关性检验

部分单指标模型(1.1)是由Carrall等于1997年首次提出的[1]，他们结合局部线性的最小二乘法构造了参数部分和非参数部分的估计量，并得到其渐近分布。此后很多学者对此模型进行了研究。

在应用研究领域，缺失数据是一种常见的数据。很多学者提出了在MAR(随机缺失)假定下解决缺失数据的方法[2]。关于缺失数据最近的研究成果可以参见文献[3-4]。

在经济和金融数据分析中,检验模型的序列相关是一项非常重要的工作。模型残差潜在的序列相关会导致估计量无效、模型预测失效等问题，很多学者对其做了深入研究[5-6]，但是很少有学者研究缺失数据下的序列相关性检验。本文研究响应变量缺失下部分单指标模型的序列相关性检验，利用经验似然方法构造检验统计量，并证明了零假设下检验统计量的渐近分布为卡方分布。

1理论与方法

1.1对缺失值进行借补

考虑如下部分线性单指标模型：

(1)

现在假设{(Xi,Yi,δi),i=1,…,n} 是来自模型(1.1)的一组不完全随机样本,其中{Yi,i=1,2,…,n}存在缺失。当δi=1时,Yi有观测值;当δi=0时,Yi缺失。 假定缺失为随机缺失(MAR)，则可以得到

即在给定Xi和Zi条件下,δi和Yi条件独立。

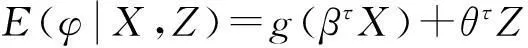
(2)

这里ei=δiεi,且满足E(ei|Xi,Zi)=0。从ei的表达式可以看出，ei和εi的序列相关结构是一致的,即检验εi的序列相关性等价于检验ei的序列相关性。下面进行ei的序列相关性检验。

设Vk=E(eiei+k),V=(V1,V2,…,Vp),k=1,2,…,p,则对ei的序列相关检验可转化为如下的原假设和备择假设：

H0:V=0↔H1:V≠0

令ωi1=eiei+1,ωi2=eiei+2,…,ωip=eiei+p,i=1,2,…,n-p,ωi=(ωi1,ωi2,…,ωip)τ。则在零假设下,E(ωi)=0;在备择假设下,E(ωi)≠0。这样,检验{ei}是否存在序列相关性就等价于检验E(ωi) 是否为0。

1.2构造经验似然比统计量

定义ωi的分布函数为F,则F的非参数似然函数为

取到最大值，从而得到经验似然比函数:

则有

(3)

对于未知的参数β，θ和g(·)的估计，通常采用两步估计法。先估计出g(·)和θ：

其中：

(4)

采用Largrange乘数法求出式(3)中关于πi的最优解,解得

(5)

其中λ为方程(6)的解。

(6)

将式(5)代入式(3)得

(7)

2数值模拟

考虑如下部分单指标模型：

数据产生如下：

β=(0.6,0.8)τ，θ=2

Xi1～U(-1,1)

Xi2～U(-1,1)

Zi～N(0,1)

Xi=(Xi1,Xi2)τ

i=1,2,…,n

① 当p(δi=1)=0.9,p(δi=0)=0.1时,即缺失概率为10%的缺失状态；

② 当p(δi=1)=0.8,p(δi=0)=0.2时,即缺失概率为20%的缺失状态；

③ 当p(δi=1)=0.8,p(δi=0)=0.4时,即缺失概率为40%的缺失状态。

样本量分别取n=100,200,300。为验证经验似然比检验的功效,本研究取显著性水平0.05各做1 000次模拟,结果如表1～6所示。

从表1～6中可以看出：在零假设条件下,经验似然比检验的size随着缺失率的增大而增大，但是随着样本量的增大,检验的size越来越接近预设的显著性水平α，检验的power会随着缺失概率的增大而减少，但是power还是较为理想。

表1　缺失概率为0.1时的AR(1)

表2　缺失概率为0.2时的AR(1)

表3　缺失概率为0.4时的AR(1)

表4　缺失概率为0.1时的MA(1)

表5　缺失概率为0.2时的MA(1)

表6　缺失概率为0.4时的MA(1)

3定理的证明

在证明过程中,由于N=n-p,因此不区别op(n) 和op(N)等。设C为绝对常数,在不同的地方取值不同。为证明定理1，给出以下几个条件：

(A1)g(·)满足一阶Lipschitz条件且其二阶倒数连续有界；

(A2) 核函数K连续有界，满足一阶Lipschitz条件，且有

(A4)βτX的密度函数是有界且紧密支撑的，并且Lipschitz连续，而且βτX在β的任意领域内任一点有有界支撑。

由文献[2]可知，上述假定条件是比较合理的。

引理1在零假设和条件A1～A6下有：

证明见文献[2]。

引理2(Abel不等式)对于任意的2个序列{ai}和{bi},i=1,2,…,n，总存在C>0,使得

其中(j1,j2,…,jn)是(1,2,…,n)的任意重排。

且对于(1,2,…,n)的任意置换(j1,j2…,jn)，也有

证明见文献[7]。

引理4在条件A1～A6和零假设下，可得

其中Ip为p阶单位阵。

证明对于任意的正整数k(1≤k≤p),有：

其中：

首先考虑Ω1,由于g(·)满足Lipschitz条件,记其Lipschitz常数为L，则有

由引理1可得Ω1=op(1)。类似可证Ω4=op(1)。

下证Ω7。

由引理1可得Ω7=op(1)。

由引理2可得

Op((nh)-1/2log1/2n)·Op(N-1/2)·

Op(n1/2logn)=op(1)

同理类似可证的Ω5=op(1)。

下证Ω8。由引理2和3可得：

同理应用引理2和3可得Ω10=op(1)。

接着证明Ω11。

N1/2op((nh)-1logn)=op(1)

然后考虑Ω15。

这样就得到

因此有

令ν为任意p维非零向量,由引理1知,在零假设下,νTφi为p步相依的随机变量序列,但对于i≠j,有

故由m步相依随机变量中心极限定理得

其中Φ=ννTσ4。由Cramer-Wold方法就可以得到引理2所要的结果。

引理5在零假设和条件A1～A2下,有

证明类似引理4的证法,可证明引理5。

引理6λ是式(6)的解，有

证明见文献[8]中引理3。

定理1的证明如下：

由引理1～6,将式(7)泰勒展开可得

经简单的计算以及由引理4～6可得

定理1证明完毕。

4结束语

当前对缺失数据的研究主要集中于对统计模型的估计和置信区间的构造上,对序列相关性的研究较少。本文采用经验似然方法检验缺失数据下的部分单指标模型的序列相关性,其研究成果有较重要的理论价值和参考价值。

参考文献：

[1]CARROLL R J,FAN J,GIJBELS I,et al.Generalized partially linear single-index models[J]. Jounrnal of the American Statistics Association,1997,92:477-489.

[2]WANG J L,XUE L G,ZHU L X,et al. estimation for a partially linear single-index models[J]. The Annals of Statistics,2010,38(1):246-274.

[3]杨宜平.协变量随机缺失下相性模型的经验似然推断及其应用[J].数理统计与管理,2011,99:367-367.

[4]ZHANG K K,GONZALEZ R,HUANG B,et al.Expectation maximization approach to fault diagnosis with missing data[J].IEEE Trans-actions on Industrial Electronics,2015,62(2):1231-1240.

[5]LIU F,CHEN G M,CHEN M.Testing serialcorrelation in partially linear errors-in-variables models based on empirical likelihood[J].Communication in Statistics Theory and Methods,2008,37(12):1905-1918.

[6]LI J B,WANG Y Y,HUANG Z S,et al.Testing serial correlation in single index models[J].Communications in Statistics,2015,44(4):1020-1035.

[7]高集体,沈红岩,梁华.部分线性模型中估计的收敛速度[J].数学学报,1995,38(5):658-669.

[8]OWEN A B.Empirical likelihood ratio for linear models.[J] Ann Statistics,1991,19:1725-1747.

(责任编辑刘舸)

Serial Correlation Test for Partial Linear Single-Index Model with Missing Response Variables

LIU Feng, GUO Si-tong, TAN Xiang-yong, KANG Xin-mei

(College of Mathematics and Statistics, Chongqing University of Technology,Chongqing 400054, China)

Abstract:We considered the serial correlation test for partial linear single-index model with response variables missing at random (MAR). Firstly, we filled in the missing response variables by the imputation method. Then we applied the empirical likelihood method to establish the test statistic, and constructed the ratio statistic of empirical likehood and derive the asymptotic distribution of the statistic. Simulation results indicate that the test method performs well.

Key words：part of single-index model; missing data; missing at random; experience likelihood; serial correlation tests

文章编号：1674-8425(2016)02-0145-07

中图分类号：O212

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.02.025

作者简介：刘锋(1973—),男,湖南新化人,博士,副教授,主要从事非参数统计研究；郭似童(1990—),女,湖北随州人,硕士研究生,主要从事非参数统计研究。

基金项目：重庆理工大学研究生创新基金资助项目(YCX2014234)

收稿日期：2015-10-12

引用格式：刘锋,郭似童,谭祥勇,等.响应变量缺失下部分线性单指标模型的序列相关性检验[J].重庆理工大学学报(自然科学版)，2016(2):145-151.

Citation format：LIU Feng, GUO Si-tong, TAN Xiang-yong, et al.Serial Correlation Test for Partial Linear Single-Index Model with Missing Response Variables[J].Journal of Chongqing University of Technology(Natural Science)，2016(2):145-151.