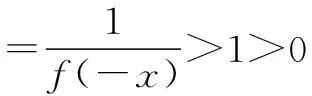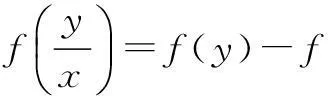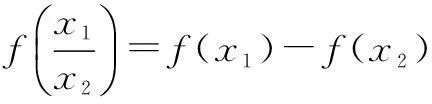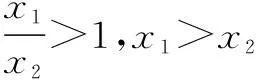○学习指导○

例说抽象函数问题的常用对策

张建军

(江苏省如东县教师发展中心，226400

抽象函数是指没有明确给出具体的函数表达式,只是给出一些条件的函数,它是中学数学函数部分的难点．本文就求解抽象函数问题的常用对策举例说明,仅供参考．

一、函数性质法

解抽象函数问题时,若能从题目的条件出发挖掘出此函数的对称性、奇偶性、周期性、单调性等性质,问题就可以解决．

1.周期函数型

分析由条件对x,y取特殊值后,就可得此函数的周期性.

将x换成x+1，得f(x+1)=f(x+2)+f(x),联立得f(x+2)=-f(x-1), 将x换成x+1，得f(x+3)=-f(x).

∴f(x+6)=f(x+3+3)

=-f(x+3)=f(x),

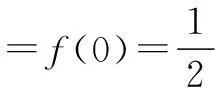
2.单调函数型

若f(x)的单调性可由题目中给出的条件得到,则可利用函数f(x)的简单图形,解决问题.

例2(2015年全国高考题)设f ′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是()

(A)(-∞,-1)∪(0,1)

(B)(-1,0)∪(1,+∞)

(C)(-∞,-1)∪(-1,0)

(D)(0,1)∪(1,+∞)

分析研究函数在(0,+∞)上的单调性,可得出f(x)的大致图象,问题就能解决.

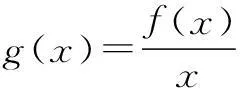
3.对称函数型

关于函数图象的对称性，有以下两个熟知的结论：

结论1函数y=f(x)的图象关于点A(a,b)对称⟺f(x)+f(2a-x)=2b,特别地，f(x)关于原点对称⟺f(x)+f(-x)=0.

结论2函数y=f(x)的图象关于直线x=a对称⟺f(a+x)=f(a-x)⟺f(x)=f(2a-x).

例3(2009年全国高考题)函数f(x)的定义域为R,若f(x+1)与f(x-1)都是奇函数,则()

(A)f(x)是偶函数

(B)f(x)是奇函数

(C)f(x)=f(x+2)

(D)f(x+3)是奇函数

分析已知f(x+1)与f(x-1)都是奇函数,就可得到f(x)的对称性，然后再向答案转化.

解∵f(x+1)与f(x-1)都是奇函数,

∴f(x+1)=-f(-x+1),

把x换成x+1，得

f(x+2)=-f(-x)；

①

又f(x-1)=-f(-x-1)，

把x换成x-1，得

f(x-2)=-f(-x).

②

由①,② 得f(x+2)=f(x-2),

把x换成x+2，得f(x+4)=f(x)，

∴函数f(x)的周期为4.

由f(x-1)=-f(-x-1)，得

f(x-1+4)=-f(-x-1+4)，

∴f(x+3)=-f(-x+3),

即f(x+3)是奇函数，故选D.

4.奇偶函数的结论

我们知道，偶函数的绝对值还是偶函数,奇函数的绝对值是偶函数,一个奇函数与一个偶函数之积为奇函数,一个奇函数与一个奇函数之积为偶函数,一个偶函数与一个偶函数之积为偶函数．此外，还有：

结论如果f(x)为偶函数,则有f(x)=f(-x)=f(|x|).

例4(2014年全国高考题)设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是()

(A)f(x)g(x)是偶函数

(B)|f(x)|g(x)是奇函数

(C)f(x)|g(x)|是奇函数

(D)|f(x)g(x)|是奇函数

分析由f(x)的奇偶性的性质得结论．

解由于偶函数的绝对值还是偶函数,一个奇函数与一个偶函数之积为奇函数,故正确选项为C.

5. 特殊函数型

有些抽象函数可由取特殊函数后得到的结果,使问题得到解决.

例5(2015年福建高考题)若定义在R上的函数f(x)满足f(0)=-1, 其导函数f′(x)满足f′(x)>k>1,则下列结论中一定错误的是()

分析此题已知函数关系,可由f(x)构造特殊函数得解.

二、函数模型法

解抽象函数问题时,若能从研究抽象函数的条件入手,通过类比,猜想出它可能是某种基本函数的模型,就可很快获得解题思路.

1.线性函数型

对任意x、y∈R,有f(x±y)=f(x)±f(y)+a,则其模型为f(x)=kx-a(k≠0).

例6(2008年重庆高考题)若定义在R上的函数f(x)满足:对任意x1,x2∈R，有f(x1+x2)=f(x1)+f(x2)+1,则下列说法一定正确的是()

(A)f(x)为奇函数

(B)f(x)为偶函数

(C)f(x)+1为奇函数

(D)f(x)+1为偶函数

分析由此函数的条件猜想f(x)=kx-1,∴f(x)+1=kx,从而很快得选项.

解令x1=x2=0,得f(0)=-1.

令x1=x,x2=-x,得

f(0)=f(x)+f(-x)+1，

∴f(x)+f(-x)+2=0，

即f(x)+1为奇函数, 故选C.

2.指数函数型

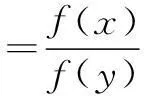
例7定义在R上的函数f(x)满足:对任意实数m,n,总有f(m+n)=f(m)·f(n),

且当x>0时,0

(1)试求f(0)的值;

(2)判断f(x)的单调性并证明你的结论;

分析根据题意,将一般问题特殊化,也即选取适当的特值,是解决有关抽象函数问题的非常重要的手段;另外,此题有一个适合题目条件的函数,如y=ax(0

解(1)在f(m+n)=f(m)·f(n)中,令m=1,n=0，得f(1)=f(1)·f(0)，

因为f(1)≠0,所以f(0)=1.

(2)任取x1,x2∈R,且设x1

∵x2-x1>0,∴0

而f(x2)-f(x1)=f(x2-x1+x1)-f(x1)

=f(x2-x1)f(x1)-f(x1)

=f(x1)[f(x2-x1)-1].

在f(m+n)=f(m)·f(n)中,令m=x,n=-x,则得

f(x)·f(-x)=1.

∵x>0时,0

∴f(x2)-f(x1)=f(x1)[f(x2-x1)-1]

<0，

∴函数f(x)在R上单调递减.

(3)首先利用f(x)的单调性,将有关函数值的不等式转化为不含f的式子.

∵f(x2)·f(y2)>f(1)，

∴f(x2+y2)>f(1),

∴x2+y2<1.

3.对数函数型

例8已知函数f(x)是满足定义域在(0,+∞)上的函数,对于任意的x,y∈(0,+∞),都有f(xy)=f(x)+f(y),当且仅当x>1时,f(x)<0成立.

(1)设x,y∈(0,+∞),求证：

(2)设x1,x2∈(0,+∞),若f(x1)

(3)解关于x的不等式

f(x2-(a+1)x+a+1)>0.

分析本题是以对数函数为模型的抽象函数,可以参考对数函数的基本性质解题.

证明(1)∵f(xy)=f(x)+f(y),

(2)∵x1,x2∈(0,+∞)时f(x1)

∵当且仅当x>1时,f(x)<0成立,

∴当f(x)<0时,x>1,

(3)令x=y=1，代入f(xy)=f(x)+f(y)，得f(1)=f(1)+f(1),故f(1)=0,f(x2-(a+1)x+a+1)>0=f(1).由(2)可知函数f(x)在定义域(0,+∞)上是减函数,∴01时,10成立;当a<1时,a0成立;当a=1,x≠1时，x2-(a+1)x+a+1>0成立．