吕诚

(安徽建筑大学数理系，安徽合肥230022)

线性规划问题中的退化最优解

吕诚

(安徽建筑大学数理系，安徽合肥230022)

通过分析退化基本可行解与取零值检验数的关系，探讨退化最优解的一些特征.得到了判断线性规划问题具有唯一退化最优解的充分条件，以及某些常见情形下的充要条件.

线性规划;单纯形法;最优解

通常线性规划问题由单纯形法进行一系列迭代后，所有检验数均小于等于零时，一定存在最优解.如果此时有等于零的检验数，需判断最优解的情况，一般都是将取值为零的检验数对应的非基变量作为新的进基变量，从而考察有没有新的最优解出现.于是很多学者都希望直接得出判断退化最优解唯一性的方法，也得到很多相关结论，但都不尽完美［1－5］.

1 基本理论与实例

对于线性规划问题的标准型［6］:

maxZ=c1x1+c2x2+…+cnxn

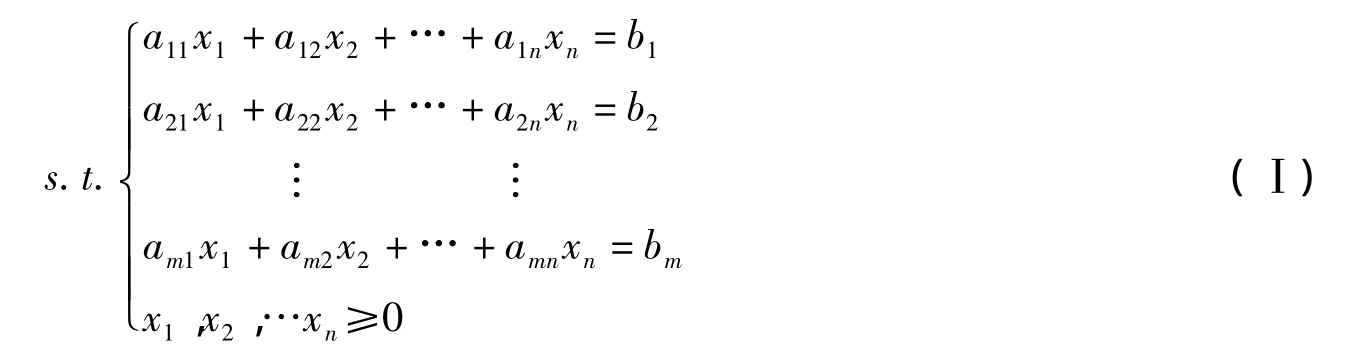
设系数矩阵秩为m，则由单纯形法可化简为最优形式:

定理1.1［1］

(1)若最优单纯形表中，所有非基变量的检验数σj皆为负数，则该线性规划问题有唯一最优解;

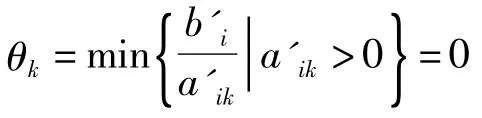
定理1.2［2］设(Ⅱ)中的σm+1，σm+2，…，σn存在多个σj=0，它们是σj1=σj2=σjp=0，p≥2.其余σj＜0，m+1≤j≤n，且j≠jr，r=1，…，p.若(Ⅱ)满足下列条件:

(1)对每个r=1，…，p，{a′i，jr∶a′i，jr＞0，i=1，…，m}≠Φ;

(2)对每个r=1，…，p有

其中l与r无关，(即b′l=0);则X*=(b1，…，bm，0，…，0)是问题(Ⅰ)和(Ⅱ)的唯一最优解.

注1定理1.1的结论(2)和定理1.2说明当存在q个检验数为零时，线性规划问题具有唯一解的充分条件是对应的q个θk等于零，但并非要求存在q个b′i等于零，甚至定理1.2说明只需一个b′l=0即可，具体可见下例.

例1

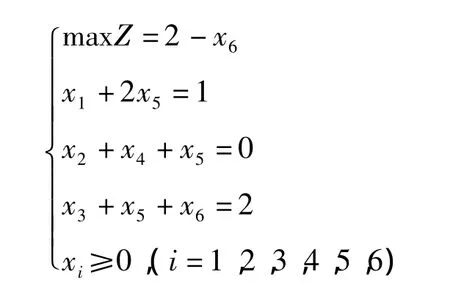
其中x1，x2，x3为基变量，并有两个检验数σ4和σ5等于零.易知θ4和θ5都取零值，且X*=(1，0，2，0，0，0)为唯一最优解，但只有b′2取值为0.

注2十分遗憾，作为线性规划问题具有唯一退化最优解的充分条件，定理1.1的结论(2)是值得商榷的.当某σk为零时，若对所有a′ik＞0，只要找到某b′l=0，可知θk=0，由定理1.1此时可以判断最优解的唯一性，但事实上并非如此，见下例.即定理1.1的结论(2)不可以作为充分条件.

例2［3］

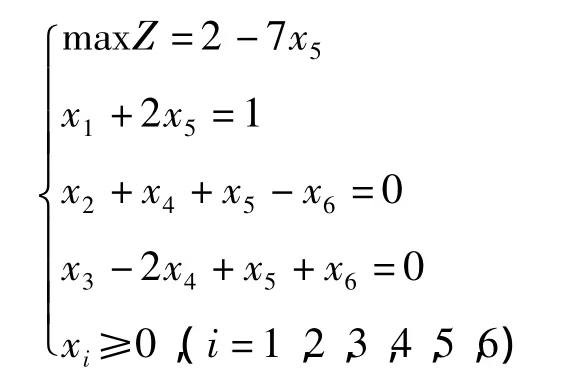
显然σ4=σ6=0，由a′2，4=1＞0且b′2=0，a′3，6=1＞0且b′3=0，满足定理1.1，按定理所得X(1)= (1，0，0，0，0，0)应该为唯一最优解，但X(2)=(1，0，1，1，0，1)也是退化的基本可行解且最优解.于是最优解并不唯一，究其原因b′2=0但a′2，6=－1＜0，以及b′3=0但a′3，4=－2＜0.

注3定理1.2作为充分条件是准确的，在条件(2)中，它比定理1.1加强了使各个θjr(=1，…，p)取值为零的条件.在文献［2］中特别强调:定理1.2中对所有θjr(r=1，…，p)，是将最小比值都落在相同的第l行，而且这一条件不可轻易去除，但同时这一条件也不是必须的(很大程度限制了定理的适用范围).

2 唯一性的判定

由注3及文献［2］可知定理1.2的条件过强，在此希望放宽定理1.2的条件，同时又易于判断，于是有如下结论.

定理2.1(充分条件)线性规划问题最优形式中有q(1≤q≤n－m)检验数σk等于零，若存在b′i1=b′i2=…=b′il=0，且对每一σk=0，都有a′i1，k，a′i2，k，…，a′il，k≥0且至少有一个a′is，k＞0时(1≤s≤l)，则该线性规划问题具有唯一最优解(q与l无关).

证明:设σk1=σk2=…=σkq=0，其余σj＜0，故对任一最优解X=(x1，x2，…，xm，xm+1，…，xn)中，当m+1≤j≤n且j≠k1，k2，…，kq时，有xj=0.再对任1≤s≤l，由第is个等式:

且b′is=0，可知

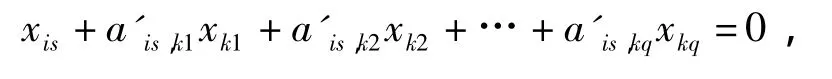
又a′is，k1，a′is，k2，…，a′is，kq≥0，故xis=b′is=0.又对1≤s≤l，至少有一个a′is，k＞0，于是由这l个等式可知对应的非基变量xk1=xk2=…=xkq=0.故此最优解是唯一的退化基本可行解.

以下进一步探讨线性规划问题具有退化的唯一最优解的充要条件.

定理2.2线性规划问题最优形式中恰有两个检验数σk=σl=0，其余σj＜0，则

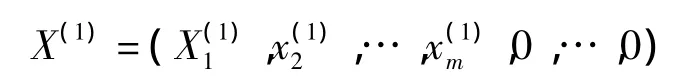
是唯一退化最优解，其中有t个基变量xi1，xi2，…，xit取值为0当且仅当(Ⅱ)满足:

(1)b′i1=b′i2=…=b′it=0，且对所有1≤s≤t，a′is，k和a′is，l都不全为零;

(2)存在一组正数μi1，μi2，…，μit，使得当μi1a′i1，k+μi2a′i2，k+…+μita′it，k=0时，

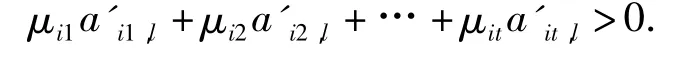
证明:“⇒”因

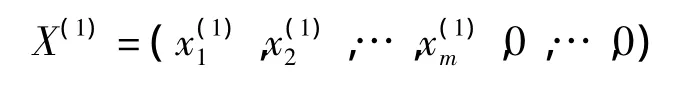
是唯一最优解，故对每一取零值的基变量xis(1≤s≤t)，由第is个等式

中所有非基变量都为零，故b′i=xis=0.又可证得若所有xk的系数a′is，k(1≤s≤t)小于等于零，则不可能有有限最优解，这与X(1)的唯一性矛盾.故对1≤s≤t，一定存在某a′is，k＞0.同理，对1≤s≤t，也存在某a′is，l＞0.同时，假设不存在定律所述的一组正数，则对任意μi1，μi2，…，μit＞0，当

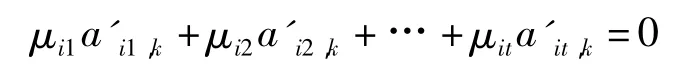
时，都有

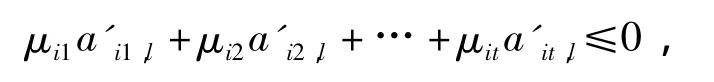
则一定不存在这样的等式:

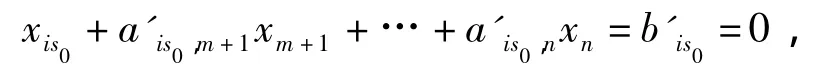
其中a′is0，l＞0且a′is0，k≥0.于是对1≤s≤t，用μis乘第is个等式，并将这t个等式相加，可得

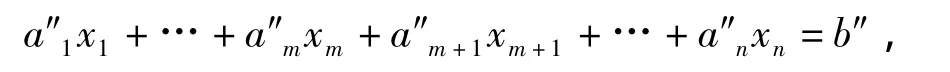
显然b″=0，并且xk的系数a″k=0，xl的系数a″l≤0，于是增大xl的取值为Dl，所得解

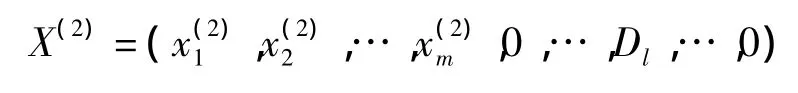
仍为最优解，这与X(1)的唯一性产生矛盾，得证.

“⇐”因σk=σl=0，其余σj＜0，由文献［6］知必存在最优解.故对任一最优解

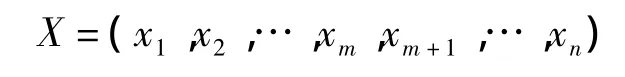
中，当m+1≤j≤n且j≠k，l时，有xj=0.由于对1≤s≤t，a′is，l不全为零，不妨设a′is0，l≠0.则由文献［7］中命题2知，xis0与xl有关系，可取xl为进基变量，xis0为出基变量.用μis乘第is个等式，并将这t个等式相加，可得

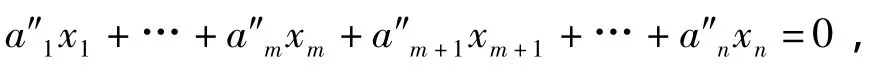
由于xl的系数a″l＞0，故xl=θl=0，即迭代后基变量xl仍取值为零，故所得的基本可行解仍为X(1).同理取xk为进基变量时，所得也仍是X(1).即X(1)为唯一退化最优解.

3 结束语

线性规划问题具有退化的最优解时，其唯一性的判定较为困难，但抓住最优解中基变量、检验数及常数取零值个数之间的关系，可以发掘出唯一退化最优解的显著特征，进而更好地加以判断.

［1］李胜，陶章华，李海波.线性规划问题最优解判别定理的研究［J］.广西大学学报，1999，24(3):197－199.

［2］闻振卫.关于最优解唯一的线性规划问题的讨论［J］.苏州大学学报，1995，11(4):12－15.

［3］杨红，刘益.线性规划最优解的唯一性问题［J］.西华师范大学学报，2008，29(1):81－83.

［4］范国兵，罗太元.线性规划问题最优解的判定［J］.长沙大学学报，2007，21(2):4－5.

［5］闻振卫.最优解唯一的线性规划问题［J］.苏州大学学报，2004，20(2):12－16.

［6］杨民助.运筹学［M］.西安:西安交通大学出版社，2000.

［7］孙秀华.单纯形法中的线性无关性［J］.宜春学院学报，2015，37(12):26－27.

The Degenerate Optimal Solutions of Linear Programming Problems

LV Cheng
(Department of Mathematics and Physics，Anhui Jianzhu University，Hefei，230022，China)

Through analyzing the relationship of basic feasible solutions and check numbers，this paper explores the characteristics of the degenerate optimal solutions.The sufficient condition for a linear programming problem which has the unique degenerate optimal solution is given.Meanwhile this paper gives the necessary and sufficient conditions in some common situations.

linear programming;simplex method;optimal solution

O221.1

A

1672－2590(2016)03－0030－04

2016－03－27

吕诚(1979－)，男，安徽六安人，安徽建筑大学数理系讲师.