王焕许， 张博洋，柴　畅，王　烁

(绥化学院 信息工程学院，黑龙江 绥化 152061)



线性分段连续型随机延迟微分方程Euler方法的收敛性

王焕许， 张博洋，柴畅，王烁

(绥化学院 信息工程学院，黑龙江 绥化 152061)

摘要：研究线性分段连续型随机延迟微分方程的数值解的收敛性，采用的是Euler方法，在处理线性项的矩阵时，证明的方法主要应用了矩阵欧几里得范数，从而达到要研究线性分段连续型随机延迟微分方程数值解的收敛性的目的，这也是本文解决问题的关键。

关键词：随机延迟微分方程；Euler方法；收敛性；数值解；矩阵欧几里得范数；

1引言与预备

考虑n维的线性分段连续型随机延迟微分方程

(1)

其中B(t)是一个布朗运动过程。

由随机微分的定义， 此方程等价于下面的积分方程

(2)

yn+1=yn+(Ayn+Byh([nh]))h+(Cyn+Dyh([nh]))ΔBn

(3)

其中 n=0,1,2,…,并且ΔBn=B(tn)-B(tn-1)，yn是x(tn)的近似解，而yh([nh])是x([nh])的近似解，为了计算简便易懂，令n=km+l(k=0,1,2,…,l=0,1,2,…,m-1)，因此(3)可以简化为下面的格式，

ykm+l+1=ykm+l+(Aykm+l+Bykm)h+(Cykm+l+Dykm)ΔBkm+l

(4)

其中ΔBkm+l=B(tkm+l)-B(tkm+l-1)，ykm+l是x(tkm+l)的近似解，而ykm是x([tkm+l])的近似解。把(4)进行连续化得到下面的式子，

(5)

其中对于t∈[tkm+l,tkm+l+1),z(t)=ykm+l,z([t])=ykm.

2Euler方法的收敛性

下面给出线性分段连续型随机延迟微分方程数值解的收敛性。首先给出两个引理。

引理1存在一个正数C1使得方程(1.2) 的解和连续的欧拉方法的数值解(5)满足

(6)

其中C1=C1(T,L2)是与h无关的常数。

证明 由(5)可得

由H¨older 不等式可得

对于所有0≤t≤T，得到

通过Doob's 鞅不等式, 得到

因此，有

由Gronwall不等式得到

其中C1=3E|x0|2exp{6(T|A|2+T|B|2+4|C|2+4|D|2)}.

同理可得

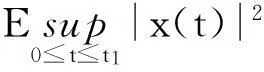
其中C1=3E|x0|2exp{6(T|A|2+T|B|2+4|C|2+4|D|2)}. 证毕。

引理2 存在一个正数C2使得下面的式子成立

(7)

其中C2=C2(T,L2)是与h 无关的常数。

证明 对于t∈[0,T]，则存在两个常数k,l使得t∈[tkm+l,tkm+l+1)，那么

y(t)=ykm+l+(Aykm+l+Bykm)(t-tkm+l)+(Cykm+l+Dykm)(B(t)-B(tkm+l))

因此，

|y(t)-z(t)|2=|ykm+l+(Aykm+l+Bykm)(t-tkm+l)

+(Cykm+l+Dykm)(B(t)-B(tkm+l))-ykm+l|2

≤|(Aykm+l+Bykm)(t-tkm+l)+(Cykm+l+Dykm)(B(t)-B(tkm+l))|2

对上面的式子取期望得到

E|y(t)-z(t)|2≤4|A|2h2|ykm+l|2+4|B|2h2|ykm|2+2h|Cykm+l+Dykm|2

因而，可得

E|y(t)-z(t)|2≤4|A|2h2|ykm+l|2+4|B|2h2|ykm|2+2h|Cykm+l+Dykm|2

≤4|A|2h2|ykm+l|2+4|B|2h2|ykm|2

+4|C|2h|ykm+l|2+4|D|2h|ykm|2

≤4(|A|2h2+|C|2h)E|ykm+l|2+4(|B|2h2+|D|2h)E|ykm|2

≤4(|A|2h2+|C|2h)C1+4(|B|2h2+|D|2h)C1

因此，

其中C2=4C1(|A|2T+|C|2+|B|2T+|D|2). 证毕。

定理1方程(1)欧拉方法的数值解收敛到其精确解

(8)

证明 由(2)和 (3)得

由H¨older 不等式有

对于所有0≤t≤T，得到

通过Doob's 鞅不等式, 得到

因此，有

≤8{T(|A|2+|B|2)+2(|C|2+|D|2)}C2h

≤8{T(|A|2+|B|2)+2(|C|2+|D|2)}C2h

由Gronwall 不等式可得

这里C3={8T(|A|2+|B|2)+16(|C|2+|D|2)}C2exp8{T(|A|2+|B|2)+2(|C|2+|D|2)}

因此，

证毕。

3结语

综上所述，本文给出了线性分段连续型随机延迟微分方程数值解的收敛性，应用的是Euler方法，方法是把离散的数值格式进行连续化后来进行证明，使得证明过程更加简洁明了，针对随机延迟微分方程的Euler方法已经有人给出，但是关于线性分段连续型随机延迟微分方程还没有研究，本文就是针对这类方程给出了其数值解的收敛性，这为以后继续研究线性分段连续型随机微分方程解析解和数值解的性质奠定了基础并提供理论根据。

[参考文献]

[1] K. L. Cooke and J. Wiener, Retarded differential equations with piecewise constant delays[J]. J. Math. Anal. ，1984,99:265-297.

[2] J. Wiener,Generalized solutions of functional differential equations[M].Singapore: World Scientic, 1993.

[3] X .Mao, Stochastic Differential Equations with markovian switching[M].London: Imperial College Press, 2006.

[4] X. Mao, Numerical solutions of stochastic differential delay equations under the generalized Khasminskii-type conditions[J].Applied Mathematics and Computation, 2011,217:5512-5524.

[5] Mao, X.: Numerical solutions of stochastic functional differential equations[J].LMS J. Comput. Math.,2003,6:141-161.

[6] Mao, X.: Exponential stability of equidistant Euler-Maruyama approximations of stochastic differential delay equations[J].J. Comput. Appl. Math.,2007, 200:297-316.

[7] 胡迪鹤.随机过程论基础、理论、应用[M].武汉：武汉大学出版社,2000:56-78.

中图分类号：TN911.8

文献标识码：A

文章编号：2095-0063(2015)06-0047-04

收稿日期：2015-09-01

基金项目：绥化学院大学生创新创业项目：一类分段连续型随机模型的Euler算法。

作者简介：王焕许(1965-)，男，黑龙江绥化人，教授，从事应用数学研究。

DOI10.13356/j.cnki.jdnu.2095-0063.2015.06.012