宋旭霞

（呼伦贝尔学院数学与统计学院 内蒙古 海拉尔 021008）

常微分方程是伴随着微积分的产生和发展而成长起来的一门历史悠久的学科，是研究自然科学和社会科学中的事物、物体和现象运动、演化和变化规律的最为基本的数学理论和方法。物理、化学、生物、工程、航空航天、医学、经济和金融领域中的许多原理和规律都可以描述成适当的常微分方程，如牛顿的运动定律、万有引力定律、机械能守恒定律，能量守恒定律、人口发展规律、生态种群竞争、疾病传染、遗传基因变异、股票的涨伏趋势、利率的浮动、市场均衡价格的变化等，对这些规律的描述、认识和分析就归结为对相应的常微分方程描述的数学模型的研究。因此，常微分方程的理论和方法不仅广泛应用于自然科学，而且越来越多的应用于社会科学的各个领域。

常微分方程既是数学分析、高等代数的后续课程，又是泛函分析、数学模型、生物数学、数理方程、微分方程数值解的先修课程。因此，在本科数学教学中， 它占有承上启下的重要地位。“常微分方程”理论体系严谨，抽象程度高，在讲授时，只有结合其广泛的应用背景，才能顺应时代要求，以实现培养具有应用能力和创新能力的专业人才的目标。

范例教学是在教学中选择真正基础的本质的知识作为教学内容，通过“范例”内容的讲授，使学生达到举一反三、掌握同一类知识的规律的方法。范例教学不仅能提高学生的学习兴趣和应用能力， 而且还有助于提高教师的业务水平，是一种重要而有效的教学方式。常微分方程教学范例都是一些成熟的数学模型，这些模型是理论知识和实际问题相结合的经典范例，是通过分析现实事件和运用数学工具建立起来的数学结构．通过常微分方程范例教学能解释现实的现象，预测未来的发展，进行优化和控制，从而科学地指导社会生活和生产实践。为了更好地加快教学改革的步伐，我们在常微分方程教学过程中尝试着引入一些具体的范例，涉及生物数学、 物理学、经济学等方面，以下是其中的几个具体范例及其分析。

一、排水问题

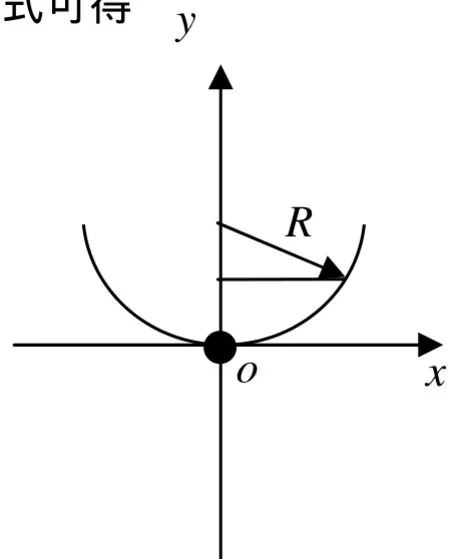
一个半径为Rcm的半球形容器内开始时盛满了水，但由于其底部一个面积为2Scm的小孔在时刻被打开，水被不断放出。问：容器中的水被放完总共需要多少时间？

解: 以容器的底部o点为原点，取坐标系如图1所示。令h(t)为t时刻容器中水的高度，可建立h(t)满足的微分方程。

这是一个一阶可分离变量的微分方程，解得

排水问题是学生比较熟悉的数学问题，通过此问题的引入，可以有效地解答可分离变量的微分方程的实际应用，有利于学生的理解与掌握。

二、热传导问题

一根长度为l的细金属杆被水平地夹在两端垂直的支架上，一端的温度恒为T1，另一端温度恒为为常数，）。若金属杆横截面积为A，截面的边界长度为B，它完全暴露在空气中，空气温度为T3，（为常数），导热系数为α，试求金属杆上的温度分布，（设金属杆的导热率为λ）。

解：一般情况下，在同一截面上的各点处温度也可能不相同，但因金属杆较细且金属杆导热系数又较大，为简便起见，不考虑这方面的差异，而建模求单变量函数。根据热传导原理：

当温差在一定范围内时，单位时间里由温度高的一侧向温度低的一侧通过单位面积的热量与两侧的温差成正比，比例系数λ与介质有关。

根据假设可知：

dt时间内T(x)通过距离o点x处截面的热量为：

dt时间内通过距离o点xdx+ 处截面的热量为：

利用泰勒公式可得

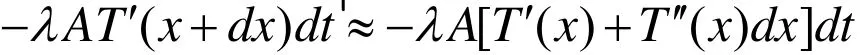
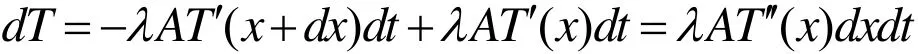
同时，金属杆的微元向空气散发出的热量为：

因系统处于热平衡状态，故有：

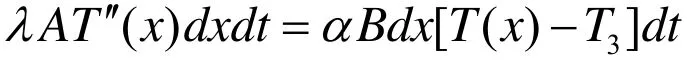
所以金属杆各处温度T(x)满足的微分方程:

这是一个二阶常系数线性方程，方程可化为

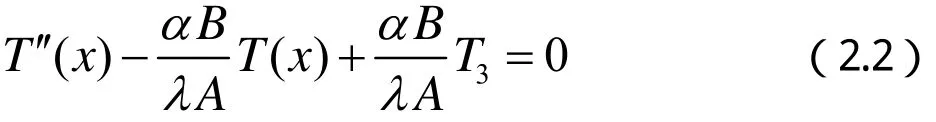
先解二阶齐次线性方程

从而得到二阶齐次线性方程的通解为

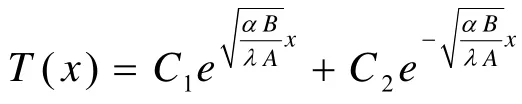
再设T*(x)=c为方程（2）的一个特解，代到方程（2.2）中得T3=c

所以方程（2.1）的通解为

热传导问题是物理上比较常见的实际问题，通过此问题的分析，可以让学生切实感受到二阶常系数线性方程的实际背景及解决办法，有利于学生的理解与掌握。

三、新产品市场营销问题

怎样才能建立一个数学模型来描述新产品的推销速度问题，并由此推出一些有用的结果以指导生产，这一直都是经济学家和社会学家非常关心的问题，下面我们讨论一个电视机新产品的销售模型。

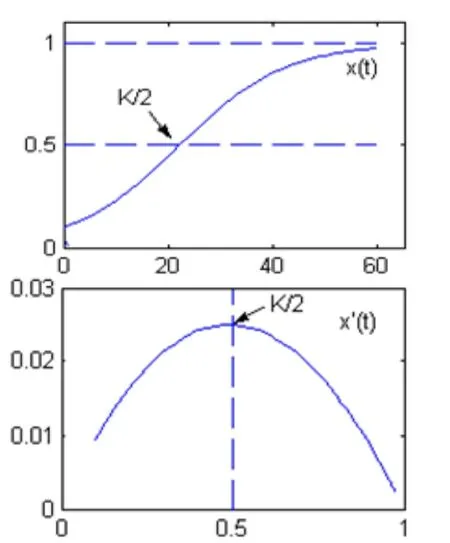
设市场需求量有一个上限，并记此上限为M，记t时刻已销售出的电视机的数量为x(t) ，则市场中尚未购买的人数大约为，那么根据统计筹算律有与成正比，记比例系数为k，则有

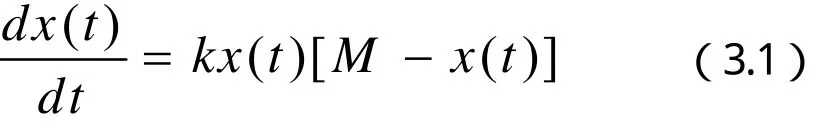
在销出量小于最大需求量的一半时，销售速度是不断增大的，销出量达到最大需求量的一半时，该产品最为畅销，接着销售速度将开始下降。所以初期应采取小批量生产并加以广告宣传；从有20%用户到有80%用户这段时期，应该大批量生产；后期则应适时转产，这样做可以取得较高的经济效果。

四、Horrod-Domer经济增长问题

分别设Y、C、I、A为总收入、总消费、引致投资和自发支出（自发消费与自发投资之和），则有总供给等于总需求可知Y=C+I+A

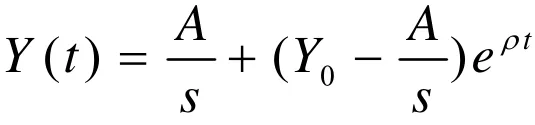
由此可见：

（1）当ρ＞r时，若，则Y(t)有常数增长率ρ；

（2）当ρ＜r，t→∞时，，即自发支出增长过快，挤掉了生产性投资，使总产量锐减，所以自发支出不宜增长过快；

（3）当ρ=r时，

说明当t→ +∞时，，造成生产萎缩。

新产品市场营销问题和Horrod-Domer经济增长模型问题都是经济学中经常讨论的实际问题，通过此类问题的分析，可以让学生切实感受到一阶线性方程的应用领域并加强了对Logistic曲线、常数变易法及积分曲线的理解。

五、传染病问题

假设总人口具有常数输入率Λ，我们把疾病流行的某市的总人口分为四类；易感类，带HIV病毒类，已得AIDS类，说服类．分别用表示t时刻易感类、被HIV病毒感染类、已发展成AIDS病人的人口数、说服率。由性传播的感染率记为β，自然死亡率记为μ，因病死亡率记为α，由带HIV病毒的发展成AIDS的转化率记为δ，说服率记为p，由于说服而不与那些高危人群接触而使AIDS病不再传播．由以上假设，利用仓室模型的建立方式我们可以建立如下动力学方程来描述这种疾病的传播过程:

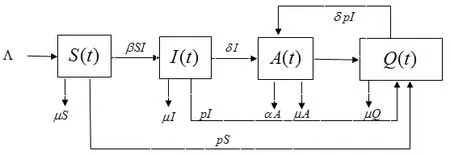
从而有

由此可得：

（1）若R0＜1，系统(5.1) 有无病平衡点，其中

（2）若R0＞1，系统(5.1)存在地方病平衡点

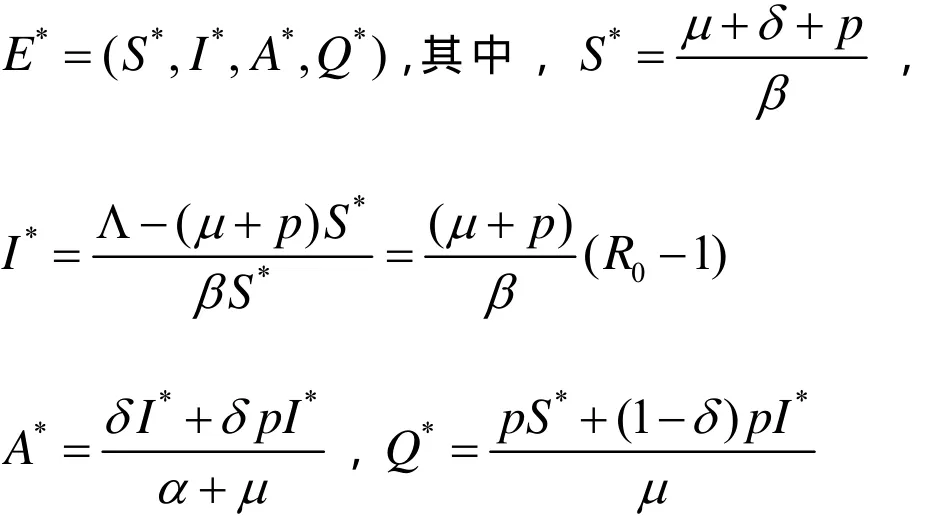
（3）若R0＜1时，无病平衡点是局部渐进稳定的；若R0＞1时，无病平衡点是不稳定的。

（4）若R0＞1时，地方病平衡点是局部渐进稳定的。

传染病动力学模型是微分方程应用的重要领域，通过讲解此模型的建立及其平衡点的稳定性的判断方法，强化了学生关于微分方程稳定性理论的理解。

通过上述常微分方程教学中实际应用范例的介绍，使学生了解微分方程源于生活实践又应用于生产实际，学习它的目的是为更好地解决实际问题．由于这些范例具有客观性、典型性和实用性，所以微分方程范例教学能把生产生活实际与数学理论紧密结合起来，并有利于学生数学思维能力和数学应用能力的提高．