李洪明

（呼伦贝尔学院数学与统计学院 内蒙古 海拉尔 021008）

基于随机性复杂系统中捕食者模型的参数估计检验和系统稳定性、可靠性分析研究，在很多领域通常都是在建立了相关的微分方程模型基础上进行的。诸如工程、物理、生物、化学、医药、生态、社会学、环境科学、人类科学、金融保险等相关领域微分方程模型都能发挥着重要的作用。在研究实际问题时，人们首先将问题数学化，各因素变量化。进一步在研究各因素的相互影响关系时，就常常会联系到某些变量的变化率或导数,最后通过研究实际问题中各因素的变化规律，以及各因素间的相互关联性所得到变量之间的关系就是我们所建立的微分方模型。然而，它反映的却是变量之间的间接关系,要得到直接关系,还需要进一步求解这一微分方程模型，对参数估计检验和系统稳定性、可靠性分析。因此，在如此广泛的实际应用领域内研究参数估计就显现其所拥有重大的实用价值和科学意义。

食饵独立生存时以指数规律增长，且食饵的相对增长率为r1，即x′=rx，而捕食者的存在使食饵的增长率减小，于是x(t)满足方程：

其中系数a反映捕食者掠取食饵的能力。

由于捕食者离开食饵无法生存，且它独立生存时死亡率为d，即y′=-dy，而食饵的存在为捕食者提供了食物，相当于使捕食者的死亡率降低，且促使其增长。设这种作用与食饵数量成正比，于是y(t)满足方程：

其中系数b反映食饵对捕食者的供养能力。

方程(1)、(2)是在自然环境中食饵和捕食者之间依存和制约的关系，这里设有考虑种群自身的阻滞作用，是Volterra提出的最简单的模型。

加入种群自身的阻滞作用，加入Logistic项，模型为：

据p为主对角线元素之和的相反数，q为其行列式的值，得：

平衡点 p q 稳定条件P1N ( 1)( 1,0)r-rσ-122-rrσ 2σ<1 1 -)2(21 P(N1σ 1(+ N(1)22-1)21+σσ,)121+σσ 1σ2 r1 1(+ r(σ-)σ+σσ 1)+221 112 rr1+12(1)(2-1)1 σ σ+σσ 12 2σ>1 P0)3(,0-r +1 r 2- 不稳定r1r2

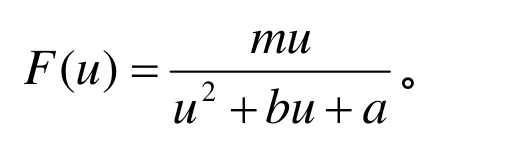
反应扩散系统模型：

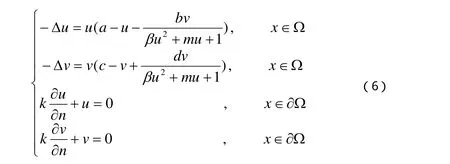
若β、m=0，可得到经典具反应扩散项的Lotka-volterra食捕模型，

解的存在性定理：

证明 设是边值的主特征值，对应特征函数为Ψ ＞ 0，正规化，maxΩΨ=1取有，其中ω，χ满足：

模型中使用的函数F1,F2分别为：

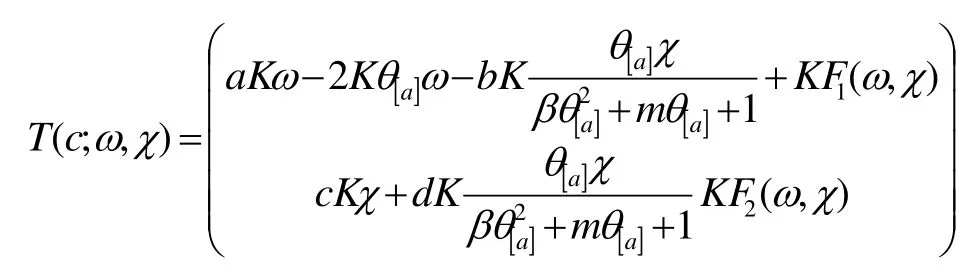
那么，T(c;ω,)χ是X上的紧可微算子，若则 G 为 c1的函数，当时，有G(c; 0,0) =0，这正是（6）的正解。

据此方法，我们可以得到随机性复杂系统中特定食捕模型的解，这个解恰为实际问题中的一个平衡点。

然而，它的稳定性与可靠性又显得尤为突出，现就平衡点的稳定性和可靠性进行。

针对P3( 0,0)；由p=-r1+r2，q=-r1r2，且r1>0,r2>0,于是q<0,故P1(N1,0)是不稳定的。