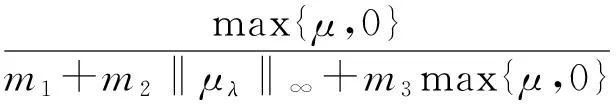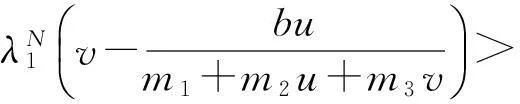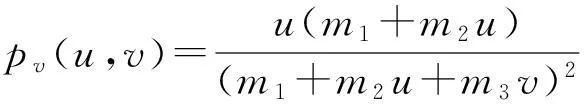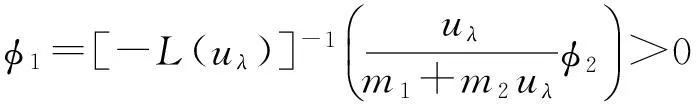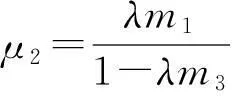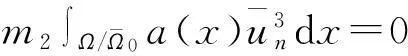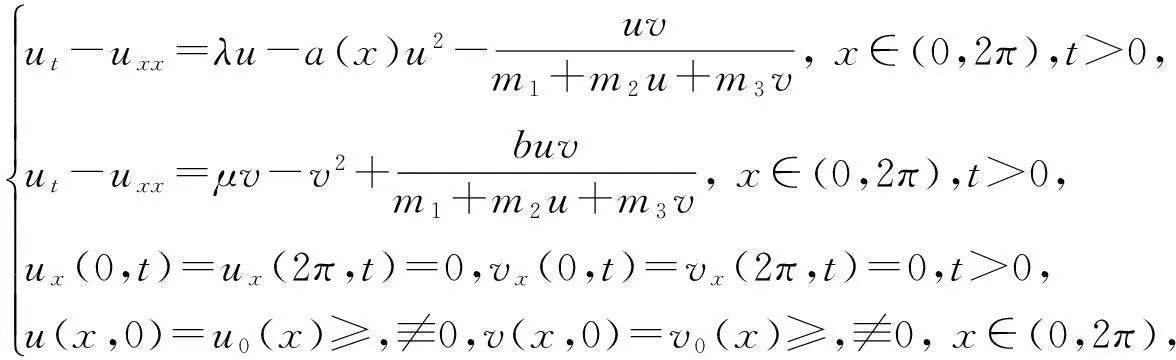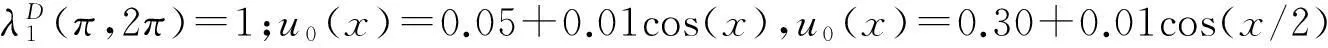一类异构捕食-食饵退化模型正解的存在性

杨文彬, 李艳玲*

(陕西师范大学 数学与信息科学学院, 陕西 西安 710119)

摘要：研究了一类空间非齐次环境下的捕食-食饵扩散模型。在食饵弱增长情形下, 利用分歧理论给出了两个半平凡解附近正解的存在性, 并刻画了整体结构;在食饵强增长情形下, 通过度理论和正则摄动理论给出了正解存在的充分条件:。鉴于空间环境的非齐次性和退化因素的存在, 通过数值算例验证了相应理论结果。

关键词:扩散; 空间非齐次; 分歧理论; 度理论; 存在性

中图分类号：O175.26文献标志码： A

文章编号：1672-4291(2015)01-0019-05

doi:10.15983/j.cnki.jsnu.2015.01.114

收稿日期：2014-09-09

基金项目：国家自然科学基金资助项目(11371012,11471200); 北方民族大学校级项目(2012Y038)

Existence of positive solutions for a predator-prey degenerate model in

heterogeneous environment

YANG Wenbin, LI Yanling*

(School of Mathematics and Information Science,

Shaanxi Normal University, Xi′an 710119, Shaanxi, China)

Abstract:A predator-prey diffusion model in heterogeneous environment is researched.For the case of weak growth of prey, the existence of positive solutions are obtained near two semi-trivial solutions by using the bifurcation theory; moreover, the global structure are given. for the existence of positive solutions are showed by the degree theory and the regular perturbation theory. Considering the spatial heterogeneity and the influence of the degradation factor, some simulations are done in order to verify the theoretical results.

Key words: diffusion; spatial heterogeneity; bifurcation theory; degree theory; existence

MR subject classification: 35K57

考虑空间非齐次环境下的一类退化的捕食-食饵模型

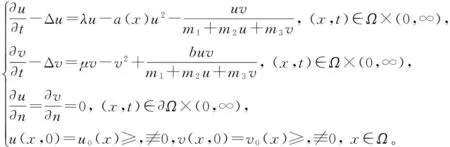
(1)

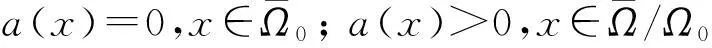
(2)

(3)

当a(x)是正常数(齐次环境下)时, 文献[3]利用正锥上的不动点指标理论分析了对应模型解的存在性、多解性和唯一性。文献[4]利用分歧理论讨论了局部和全局分歧解的存在性并通过隐函数定理和广义最大值原理说明了正解的存在唯一性。Du和Hsu[5]在空间齐次环境下, 通过构造Lyapunov函数研究了对应模型全局吸引子的存在性;在非齐次环境下,利用分析方法说明了对应模型正解的存在性。文献[6]研究了在空间非齐次环境下一类捕食-食饵模型正平衡态的存在性和稳定性。本文主要涉及的方法有分歧理论和拓扑度理论[7-9]。

为了得到系统(3)解的性质,首先考察以下椭圆方程:

(4)

1分歧解的存在性

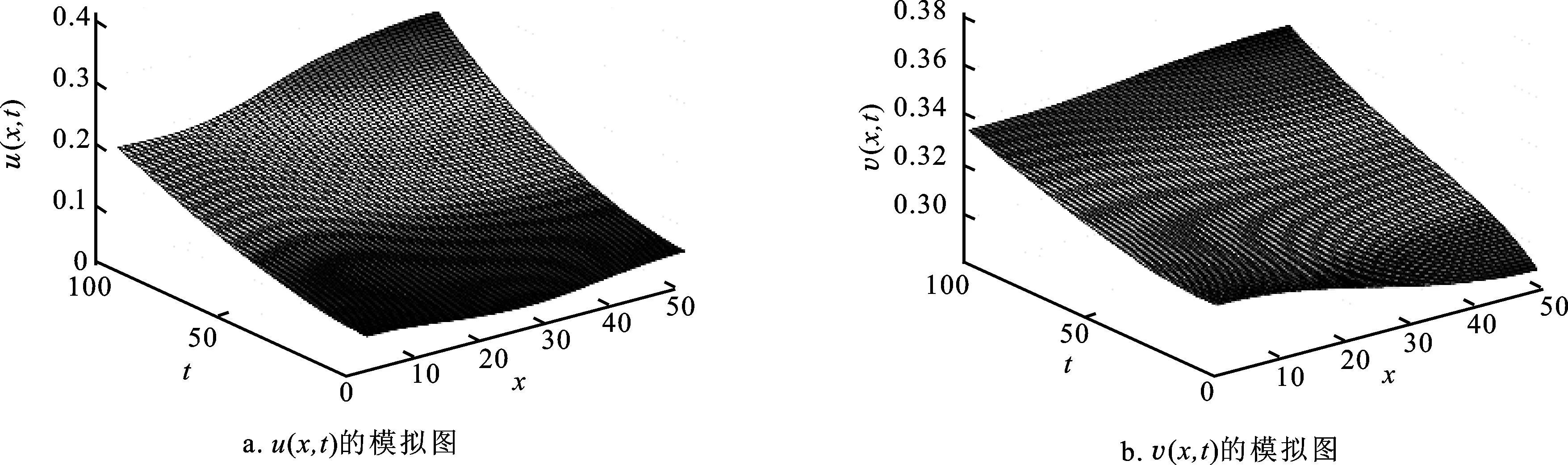
(ⅰ) 0

max{μ,0}

(ⅱ) 参数μ满足

(5)

证明由标准比较原理,结论(ⅰ)成立。现在证明结论(ⅱ)。

由u、v的方程, 结合结论(ⅰ)得

由λ<1/m3可知，

引理得证。

对p>1,令

G(μ,w,v)=

(6)

此时，系统(3)等价于G(μ,w,v)=0,而且(u,w)=(0,0)是G的平凡解。通过简单计算可知，

Gu(w,v)(μ,w,v)[φ,ψ]=(0,ψ)T。

(7)

Γ1={(μ(s),uλ(x)-w(s),v(s)):s∈[0,δ)},

(8)

zi(0)=0,i=1,2。

此时,记u(s)=uλ(x)-w(s)。将(μ(s),u(s)-w(s),v(s))代入系统(3)的第2个方程，方程两边同时除以s,再对方程两边在s=0处求导，最后在Ω上积分可得

μ′(0)=

(9)

即(μ1,uλ,0)附近分歧曲线Γ1是超临界的。

Γ2={(μ(s),u(s),μ+w(s)):s∈[0,δ)},

(10)

zi(0)=0,i=1,2。类似(9)式，有

μ′(0)=

2正解的存在性(度理论)

‖un‖∞+‖vn‖∞≤C。

(12)

证明令(un,vn)是用μn代替μ后系统(3)的正解。因为μn≤M，所以

(13)

进而，‖vn‖∞≤M+b/m2。假设结论不成立，那么当μ=μn时，系统(3)存在正解序列{(un,vn)}使得，当n→∞时，‖un‖∞→∞。

∫Ω|

(λ+1)|Ω|。

(14)

(15)

取光滑函数φ，使得suppφ⊂Ω0。在方程(15)两边同时乘以φ,在Ω0上积分可得

∫Ω0φφdx-

(16)

(17)

(18)

由于当n→∞时，

对以上不等式两边求极限可得

(19)

为讨论系统(3)正解的存在性，首先考虑以下摄动系统:

(20)

(21)

其中(uμ,vμ)是系统(3)的正解，M在引理3中定义。

(22)

易知，对任意μ∈[-b/m2,M]和∈[0,1],Aμ,是W到P上的紧算子。对于固定的(μ,)，Aμ,在W中的不动点即是系统(20)的非负解。特别地，如果=0，那么Aμ,在W中的不动点即是系统(3)的非负解。

对于任意μ∈[-b/m2,M]，当(u,v)∈∂W时，Aμ,0(u,v)≠(u,v)。由标准紧性理论知，存在0>0使得，对于任意μ∈[-b/m2,M],∈(0,0],Aμ,0(u,v)≠(u,v);Aμ,相对P的固定点指标indexP(Aμ,,W)有定义，而且与(μ,)无关。

当μ<0时，系统(20)存在唯一非负常数解(0,0);当μ>0时，系统(20)存在非负常数解(0，0)和(0，μ)。对任意∈(0,0],由Dancer[13-14]不动点指标计算(可以验证(0,0)和(0,μ)都是非退化的。在此，省去不动点指标的计算过程)可知：

当μ≠0时，indexP(Aμ,,(0,0))=0;

由Aμ,的不动点指标关于μ的不变性知，对任意,

indexP(Aμ,,W)=indexP(Aμ1,,W)=0。

(23)

indexP(Aμ,,W)=indexP(Aμ,,(0,0))+

indexP(Aμ,,(0,μ))=0+1=1

与(23)矛盾。因此，系统(20)在W中存在另外的解(uμ,,vμ,),而且。对于存在的任意非负解(uμ,,vμ,),则由标准紧性理论知,存在(uμ,vμ),使得如果需要可以取其子列,(uμ,n,vμ,n)→(uμ,vμ)。

假设vμ,≡0。因为,经过对uμ,n的方程进行极限分析可知uμ=0,即(uμ,vμ)=(0,0)。这与(0，0)是系统(20)的退化解相矛盾,所以vμ,>0。即当时，系统(20)存在正解。可知，系统(20)的任意正解(u,v)满足v>μ,故而vμ≥μ>0。假设uμ=0,因为,经过对vμ,n的方程进行极限分析可知vμ=μ,即(uμ,vμ)=(0,μ),这与(0,μ)是系统(20)的退化解相矛盾，所以uμ>0。故而，当n→0时，{(uμ,n,vμ,n)}收敛到系统(3)的一个正解(uμ,vμ)。结论证毕。

3数值算例

考察系统(1)在一维空间下对应的系统(24)，验证定理2结论下系统(3)正解的存在性，

(24)

容易验证，以上参数均满足定理2中系统(3)正解的存在性条件。借助Matlab软件，利用有限差分方法对系统(24)进行模拟仿真，其中空间尺度为x∈(0,2π),时间尺度为t∈(0,T),T=10,空间和时间网格间距分别为Δx=2π/49,Δl=10/99。具体数值结果见图1和图2。

图1系统(24)正解u、v的模拟图

Fig.1The simulation diagram of the positive solutionuandvof system (24) respectively

图2图1在T=10时刻的剖面图

Fig.2The profile of figure 1 at the timeT=10,

可以理解为系统(3)的正解

4结语

本文在齐次Neumann边界条件下研究了一类空间非齐次环境下的捕食-食饵扩散模型。鉴于空间环境的非齐次性和退化因素的影响,分别在在食饵弱增长和强增长情形下,利用分歧理论, 拓扑度理论和正则摄动理论说明了正解的存在性。但是无论是食饵弱增长还是强增长情形,对于系统(3)正解的存在性分析中,总是假设λ<1/m3。对于λ≥1/m3的情况, 文中部分方法失效, 该类问题有待进一步研究。

参考文献：

[1] Beddington J R. Mutual interference between parasites or predators and its effect on searching efficiency[J]. Journal of Animal Ecology, 1975, 44:331-340.

[2] DeAngelis D L, Goldstein R A, O′Neill R V. A model for trophic interaction[J].Ecology, 1975, 56:881-892.

[3] Guo Gaihui, Wu Jianhua. Multiplicity and uniqueness of positive solutions for a predator-prey model with B-D functional response[J].Nonlinear Analysis, 2010, 72(3/4):1632-1646.

[4] 郭改慧, 吴建华. 一类具有扩散的捕食-食饵模型正解的存在性和唯一性[J].数学物理学报, 2011, 31A(1): 196-205.

[5] Du Yihong, Hsu S B. A diffusive predator-prey model in heterogeneous environment[J].Journal of Differential Equations, 2004, 203(2): 331-364.

[6] Peng Rui, Wang Mingxin. Uniqueness and stability of steady states for a predator-prey model in heterogeneous environment[J].Transactions of the American Mathematical Society, 2008, 136(3): 859-865.

[7] 李海侠, 李艳玲. 一类带有C-M反应函数的捕食-食饵模型正解的存在性和唯一性[J].陕西师范大学学报: 自然科学版, 2014, 42(2): 7-12.

[8] 姚若飞, 李艳玲. 具有阶段结构的捕食-食饵模型的定性分析[J].陕西师范大学学报:自然科学版, 2013, 41(1): 10-14.

[9] 王丽娟, 李艳玲. Oregonator模型的平衡态正解分析[J]. 陕西师范大学学报:自然科学版, 2012, 40(3):6-11.

[10] 叶其孝，李正元. 反应扩散方程引论[M].北京: 科学出版社, 1994.

[11] Du Yihong, Shi Junping. Allee effect and bistability in a spatially heterogeneous predator-prey model[J].Transactions of the American Mathematical Society, 2007, 359(9):4557-4593.

[12] Crandall M G, Rabinowitz P H. Bifurcation from simple eigenvalues[J].Journal of Functional Analysis, 1971, 8:321-340.

[13] Dancer E N. On the indices of fixed points of mappings in cones and applications[J].Journal of Mathematical Analysis and Applications, 1983, 91(1):131-151.

[14] Dancer E N. Multiple fixed points of positive mappings[J].Journal fur die Reine und Angewandte Mathematik, 1986, 371:46-66.

〔责任编辑宋轶文〕

第一作者： 范亚静, 女, 讲师, 博士研究生, 主要研究方向为算子代数与量子信息。E-mail:fanyajing119@163.com