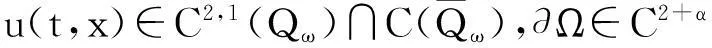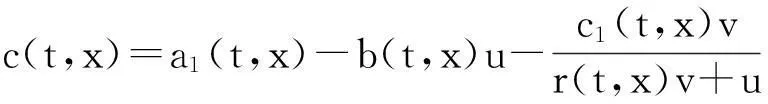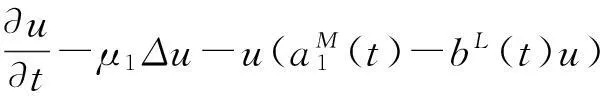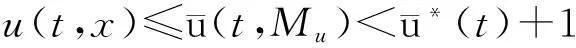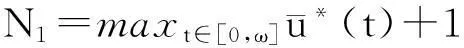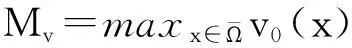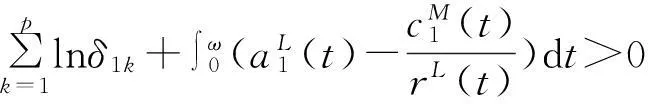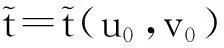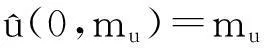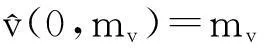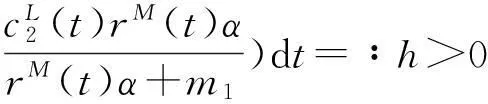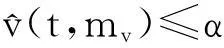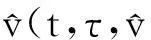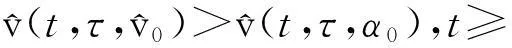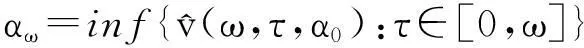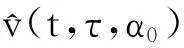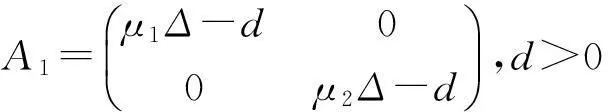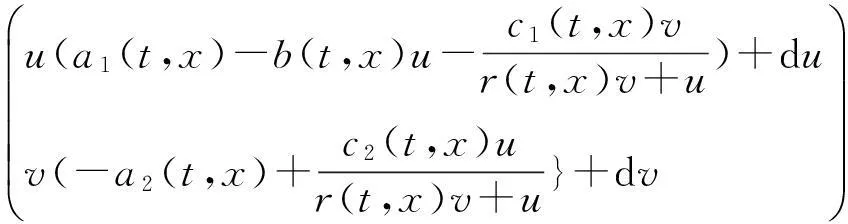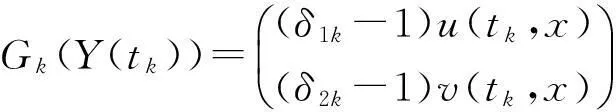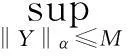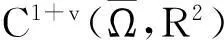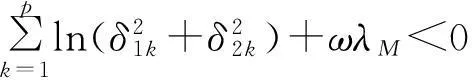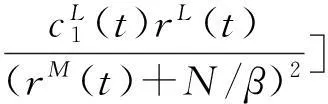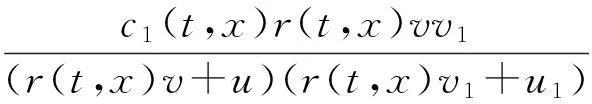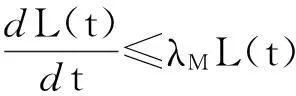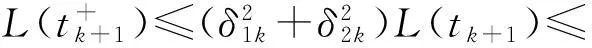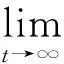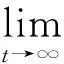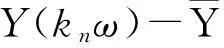李　婧, 窦家维

(陕西师范大学 数学与信息科学学院, 陕西 西安　710062)



具有扩散及功能性反应的周期脉冲捕食-被捕食系统研究

李婧, 窦家维*

(陕西师范大学 数学与信息科学学院, 陕西 西安710062)

摘要：主要研究了一类具有扩散及功能性反应的周期脉冲捕食-被捕食系统, 系统由一个具有脉冲的反应扩散方程组描述.首先通过抛物偏微分方程的不变矩形理论获得了解的正性性质,然后利用比较原理研究系统解的有界性及持续生存性质;最后应用紧性准则讨论了系统周期解的存在唯一性及全局渐近稳定性.

关键词：捕食-被捕食系统; 功能性反应; 脉冲收获; 持续生存性; 周期解

0引言

种群动力学模型对种群生态学研究有着非常重要的意义,在种群动力学中,捕食关系因其普遍存在性和重要性一直是数学与生态学界研究的主要课题[1-4].在种群动力学模型的早期研究中,人们常假设种群在各处的密度分布是均匀的, 因此可以应用常微分方程模型来描述种群的发展过程. 然而, 在种群的栖息地内, 如果各处种群密度分布不均匀, 那么种群密度函数不仅与时间有关, 也与位置变量有关, 并且种群中的个体将自发地从高密度地区向低密度地区扩散, 这种情况下, 种群系统就需要用反应扩散方程来描述[5-8].

本文主要研究一类具有扩散及比率依赖功能性反应的捕食系统的动力学行为. 在捕食系统中考虑功能性反应能更确切地描述食饵与捕食者的捕食关系. 功能性反应函数有多种形式, 常见的有比率依赖型和食饵依赖型, 比率依赖意指功能性反应函数是食饵与捕食者比率的函数. 近年来, 许多生物学家研究发现比率依赖型的功能性反应更具有实用性, 因此得到了广泛的应用[9-15].

本文还假设由于季节变化等因素, 种群生长环境是周期性变化的, 并且每隔一定的时间, 对种群进行脉冲比例收获[16-17].

本文所研究的系统将由下面具有周期系数的脉冲反应扩散方程组描述:

(1)

其中,u(t,x),v(t,x)分别表示食饵及捕食者的密度.系统的前两个方程表示捕食系统,Δu为Laplace算子,μ1Δu,μ2Δv表示两种群的扩散,扩散系数μ1,μ2均为正常数.系统第三,四方程表示在时刻tk,k∈N+对两种群进行比例收获,收获系数分别为δ1k及δ2k;系统的最后两个方程是边界条件.

对于(1),本文假设下面条件(H)成立:

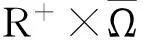
(H2)函数ai(t,x),ci(t,x)(i=1,2)以及b(t,x),r(t,x)关于t是ω-周期的;

(H3)对所有i=1,2.k∈N+,0<δik<1存在正整数p,使tk+p=tk+ω,δi(k+p)=δik.

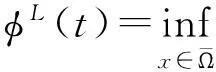
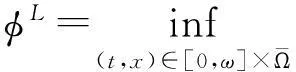
在本文的研究中, 下面几个基本结论将多次用到, 现叙述如下(参见[6]) 首先, 记

Qω=(0,ω]×Ω,Sω=(0,ω]×∂Ω.则有

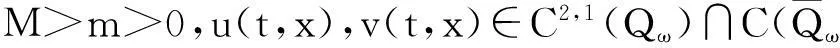
如果又有当x∈Ω时u(0,x)不恒等于v(0,x),则u(t,x)

1系统的持续生存性

定理1假设条件(H)成立, 则对于系统(1),R2的非负象限和正象限是不变的.

(2)

由于当(u,v)∈[0,M1]×[0,M2],且t≠tk(k∈N+)时,

f1(t,x,u,v)|u=0=0,f1(t,x,u,v)|u=M1<0;

f2(t,x,u,v)|v=0=0,f2(t,x,u,v)|v=M2<0.

因此,根据文献[6],并考虑到假设条件(H3),可知Π=[0,M1]×[0,M2]是系统(1)的不变矩形.所以,当u(0,x)≥0,v(0,x)≥0时,系统(1)的(u(t,x),v(t,x))满足u(t,x)≥0,v(t,x)≥0,因此R2的非负象限是不变的. 又由(2),u(t,x)满足

(3)

下面的结果给出了系统(1)解的最终有界性. 便于叙述, 记(u0,v0)=(u0(x),v0(x)), 其中u0(x)=u(0,x),v0(x)=v(0,x).

定理2假设条件(H)成立, 进一步假设

(4)

(5)

证明: 假设(u(t,x,v(t,x))是系统(1)具有非负初值(u0,v0)的解.

(i)首先证明u(t,x)的最终有界性.

(6)

的解. 因为

(ii)证明v(t,x)的最终有界性.

(7)

定理3假设(H)成立,进一步假设(5)式和下面两个不等式成立:

(8)

(9)

证明:设(u(t,x),v(t,x))为系统(1)具有非负初值(u0,v0)的解. 由于(5)式和(8)式保证了定理2的条件成立, 无妨设当t≥0时,有0≤u(t,x)≤N1,0≤v(t,x)≤N2(N1,N2为两个正常数).

(i)首先证明m1的存在性.

(10)

(ii)下面研究捕食者的持续生存问题.

(11)

由引理1知

(12)

由条件(9), 可以选择α>0充分小, 使得下式成立:

上面结果说明:

2周期解的存在唯一性

为了讨论系统(1)正周期解的存在唯一性及稳定性, 需要下面的紧性准则[16]引入记号Y=(u,v)∈Lp(Ω)×Lp(Ω),其中p>n为正整数, 将系统(1)的前四式重写如下:

(13)

F(t,Y)=

引理3[16]假设函数Gk是连续可微的, 并且存在一个正值函数η(M)使

关于周期解的存在唯一性, 可以证明下面结论.

定理4假设条件(H)成立,而且系统是持续生存的,即存在正数β和N,当t充分大时,有β≤u(t,x)≤N,β≤v(t,x)≤N成立.若系统(1)还满足下面不等式

(14)

其中λM为矩阵(aij)2×2的最大特征值,

则系统(1)有全局渐近稳定的正ω-周期解.

证明:设(u(t,x),v(t,x)),(u1(t,x),v1(t,x))为系统(1)的任意两个有界解,设其下界为β,上界为N.考虑函数

L(t)=∫Ω[(u(t,x)-u1(t,x))2+

(v(t,x)-v1(t,x))2]dx.

对其求导, 得到:

-2μ1∫Ω|(u-u1)|2dx-

2μ2∫Ω|(v-v1)|2dx+

2∫Ω(u-u1)2(a1(t,x)-b(t,x)(u+u1)-

2∫Ω(v-v1)2(-a2(t,x)+

2∫Ω(u-u1)(v-v1)

∫Ωa11(u-u1)2dx+∫Ωa22(v-v1)2dx+

2∫Ωa12(u-u1)(v-v1)dx≤

λM∫Ω[(u-u1)2+(v-v1)2]dx.

(15)

下面进一步讨论系统(1)正周期解的存在唯一性. 记Y=(u,v)首先有

因此,‖Gk(Y)‖≤δ‖Y‖,其中

δ=max{δik+1,i=1,2,k=1,2,…,p}.

sup‖Y‖a≤M‖Gk(Y)‖α≤sup‖Y‖a≤Mδ‖Y‖α≤δM=∶η(M).由于引理3的条件满足,因此,(u(t,x),v(t,x)),(u1(t,x),v1(t,x))在C1+v上有界,结合(15)可知:当t→∞时

(16)

由(16)式可知, 如果系统(1)的周期解存在, 则周期解唯一, 并且是全局渐近稳定的.

‖Y(ω,Y(knω)-Y(knω))‖C+

3数值例子

本节通过一个具体例子验证前面所得到的理论结果. 对于系统(1), 令

a1(t,x)=0.2sint+0.25+0.000 1cosx,

a2(t,x)=0.4,b(t,x)=0.1cost+0.2,

c1(t,x)=0.05cost+0.08,

c2(t,x)=0.45-0.03sint,

r(t,x)=15-5cost,

δ1k=0.8,δ2k=0.89,ω=2π,p=1.

显然满足条件(H), 又经计算可知:

所以式(5)、(8)、(9)成立. 进一步验证(14)式.又令β=10,N=25,算得a11=-1.101,a12=a21=0.178,a22=-0.608.所以λM=-0.550 4,进而ln(0.82+0.892)-0.550 4×2π=-3.099 1<0. 即(14)式成立. 故满足定理4的条件, 所以由定理4可知, 系统有全局渐近稳定的周期解.

4结论

本文研究了一类由脉冲反应扩散方程描述的捕食系统的动力学行为. 研究的基本思想是运用比较原理, 即引理1, 应用脉冲常微分系统的解对脉冲反应扩散方程的解进行估计, 主要应用脉冲常微分方程的相关理论和分析技巧研究解的有界性和持续生存性, 并应用一些分析技巧获得了周期解的存在唯一性. 在文献[15]中, 作者研究了类似问题, 但所用的比较系统大多是常系数系统,本文应用周期脉冲常微分系统作为比较系统,主要结论推广改进了文献[15]的结论. 本文的结果可为控制生物种群的共存及发展趋势提供理论依据, 研究结果有一定的现实意义.

参考文献

[1]肖燕妮,周义仓,唐三一.生物数学原理[M].西安:西安交通大学出版社,2008:41-50.

[2]陈兰荪,孟新柱,焦建军.生物动力学[M].北京:科学出版社,2009:87-102.

[3]Z.Amine,R.Ortega.Aperiodicpredator-preysystem[J].JournalofMathematicalAnalysisandApplications, 1994(185):477-489.

[4]卢琨.一类具有脉冲效应的捕食系统分析[J].陕西科技大学学报(自然科学版),2011,29(3)：155-158.

[5]LakshmiNarayanGuin,PrashantaKumarMandal.Spatiotemporaldynamicsofreaction-diffusionmodelsofinteract-ingpopulations[J].AppliedMathematicalModelling,2014,38(17-18):4 417-4 427.

[6]叶其孝,李正元.反应扩散方程引论[M].北京:科学出版社,1990:31-57.

[7]MurryJD.Mathematicalbiology[M].NewYork:Springer-Verlag,1989.

[8]岳宗敏,白云霄,曹慧,等.庇护效应下一类改进的Holling-Tanner反应扩散捕食模型的定性分析[J].陕西科技大学学报(自然科学版),2014,32(2)：159-163.

[9]MFan,QWang,XZou.Dynamicsofanon-autono-mousratio-dependentpredator-preysystem[J].Proc.Roy.Soc.EdinburghSect.A,2003,133:97-118.

[10]TKKar,SMisra,BMukhopadhyay.Abio-economicmodelofaratio-dependentpredator-preysystemandoptimalharvesting[J].JournalofAppliedMathematicsandComputing,2006,9(11):387-401.

[11]RArditi,LRGinzburg.Couplinginpredator-preydynamics:Ratio-dependence[J].Theret.Biol,1989,139:1 123-1 128.

[12]HRAkcakaya,RArditi,LRGinzburg.Ratio-depen-dentpredation:Anabstractionthatworks[J].Ecology,1995,76:995-1 004.

[13]XiaoHongLi,ChunLu,XiuFengDu.Permanenceandglobalattractivityofadiscretesemi-ratio-dependentpredator-preysystemwithholling-IVtypefunctionalresponse[J].JournalofMathematicalResearch&Exposition,2010,30(3):442-450.

[14]PYHPang,MWang.Qualitativeanalysisofaratio-depe-ndentpredator-preysystemwithdiffusion[J].Proc.Roy.Soc.EdinburghSect.A,2003,133:919-942.

[15]MUAkhmet,MBeklioglu,TErgenc.Animpulsiveratio-dependentpredator-preysystemwithdiffusion[J].NonlinearAnalysis:RealWorldApplications,2006,7:1 255-1 267.

[16]DDBainov,PSSimeonov.Impulsivedifferentialequations:Periodicsolutionsandapplications[M].NewYork:LongmanScientific&TechnicalPress,1993:58-79.

[17]VLakshmikantham,DDBainov,PSSimeonov.Theoryofimpulsivedifferentialequations[M].Singapore:WorldScientific,1989.

Thestudyonaperiodicimpulsivepredator-preysystem

withdiffusionandfunctionalresponse

LIJing,DOUJia-wei*

(SchoolofMathematicsandInformationScience,ShaanxiNormalUniversity,Xi′an710062,China)

Abstract:In this paper,an impulsive predator-prey system with diffusion and functional response is investigated.The system is modeled by a reaction-diffusion equation with periodic coefficients and impulses.The positive property of the solution is obtained by invariant rectangle of parabolic partial differential equations.Further, the comparison principle is applied to study the boundedness of the solution and the persistence of the system.Finally,the condition to ensure the existence and stability of the periodic solution is obtained by a compactness criterion.

Key words:predator-prey system; functional response; impulsive harvest; persistence; periodic solution

中图分类号：O175.1

文献标志码：A

文章编号：1000-5811(2015)05-0186-06

作者简介:李婧(1990-),女,河南三门峡人,在读硕士研究生,研究方向:脉冲微分方程理论及应用

通讯作者:窦家维(1963-),女,陕西西安人,副教授,博士,研究方向： 脉冲微分方程理论及应用，jiawei@snnu.edu.cn

基金项目：国家自然科学基金项目(61272435)

收稿日期:*2015-04-13