范志辉 陈飞武

(北京科技大学化学与生物工程学院化学与化工系; 功能分子与晶态材料科学与应用北京市重点实验室, 北京 100083)

二阶多参考态微扰理论计算电子亲和势

范志辉 陈飞武*

(北京科技大学化学与生物工程学院化学与化工系; 功能分子与晶态材料科学与应用北京市重点实验室, 北京 100083)

采用二阶多参考微扰理论计算了F, Cl, OH, SH, CN, CH2和NH2的电子亲和势. 另外, 还考察了基函数和完全活性空间大小对电子亲和势精度的影响. 通过和CASSCF, CASPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP和B2PLYP的计算结果比较发现, 针对目前所用的基函数,二阶多参考态微扰理论的总体计算效果是最好的.

电子亲和势; 多参考态微扰理论; 基函数; 完全活性空间

1 Introduction

Koopmans' theorem1provides one simple approach to calculate theoretically the electron affinity (EA) at the Hartree-Fock level. However, due to the neglect of relaxation in Koopmans' theorem, the computed EA value at this level tends to be too small in comparison with the experimental data. To deal with this problem it is chosen to calculate the energies of a neutral species and its negative ion separately and take the difference as the EA. But it turns out that computing this difference is much challenging for computation chemistry, which requires a balanced description of both the neutral system and anion. Since the anion has one more electron than its neutral counterpart its correlation energy is also larger than that of the latter. Therefore, a post Hartree-Fock calculation should be performed for obtaining an accurate EA value. The term “accurate” here will imply agreement with experiment to 0.1 eV or better. However, this level of accuracy has been proven to be very difficult to achieve.

Density functional theory has been widely used to calculate the electron affinity as well as other properties of molecular systems,2–10its accuracy depends on the basis set and the density functional used in the study. Multireference perturbationtheory is one of the important methods beyond the Hartree-Fock approximation. It combines the static and dynamic correlation effects into one single framework and provides versatile ways to describe the electronic structures of atomic and molecular systems. There are many research works on this field.11–40To list just a few, there are Hylleraas variational perturbation theory by Cave and Davidson,11CASPT2 and CASPT3,12multireference Møller-Plesset perturbation theory of Hirao,13,14multireference open-shell perturbation theory of Kozlowski and Davidson,15,16the second order generalized van Vleck perturbation theory of Hoffmann et al.,17,19the state-specific multireference perturbation theory of Mukherjee et al.,18the configuration-based multireference second order perturbation theory of Wen et al.20,36, the n-electron valence state perturbation theory of Angeli et al.,21,22the multireference perturbation theory of Chen et al.,23the multiconfiguration perturbation theory of Surján et al.,24,25,32the valence bond perturbation theory of Wu et al.,29,40a spin adapted size extensive state specific multireference perturbation theory of Liu et al.,33,34the orbitally invariant multireference perturbation theory of Chen and Hoffmann,35the block correlated perturbation theory of Xu and Li,37the size extensive multireference perturbation theory of Chen and Fan,38and SDS-MS-MRPT2 by Liu and Hoffmann.39In spite of substantial works on the perturbation theory as shown above, their applications to electron affinity problems are not as many as one may expect.

In this study, we will compute the electron affinities of F, Cl, CN, OH, SH, CH2, and NH2with the second order multireference perturbation theory.23Comparisons with the complete active space self-consistent field (CASSCF),41CASPT2,12the coupled cluster with single and double excitations (CCSD),42–45CCSD plus the perturbation correction of triple excitations (CCSD(T)),46and density functional theories such as B3LYP,47–49X3LYP,50M06,51HTCH,52TPSS,53B97D3,54mPW2PLYP,55and B2PLYP,56will be made to show their different performances. Especially, the effects of basis sets and size of the reference spaces on EA will be investigated and discussed in details.

2 Computational method

The second and third order multireference perturbation expressions can be written as follows1,23

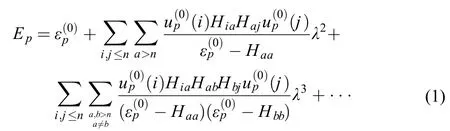
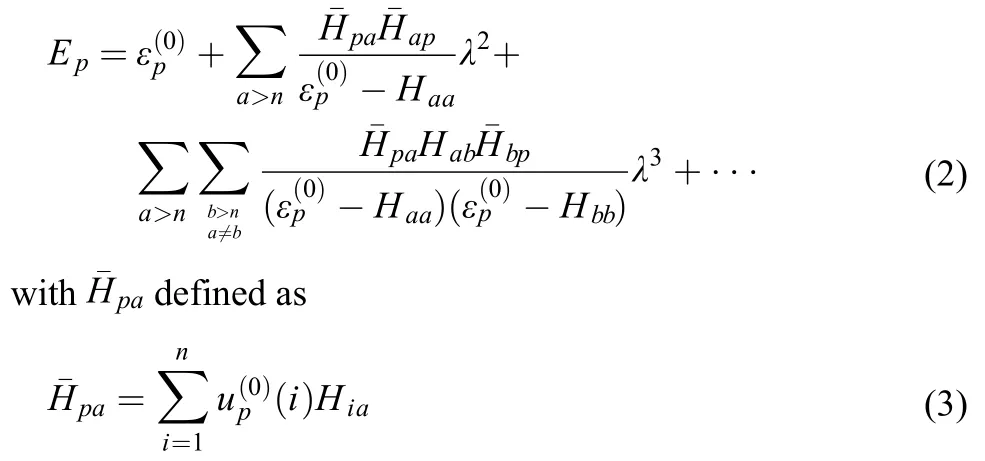
Eq.(2) is to some extent formally similar to the single reference perturbation expressions.1,23But the key differences lie in the expression ofto which not only the p-th state but also other states within the reference space have contributions to the energy Ep.

The electron affinities of F, Cl, OH, CN, SH, CH2, and NH2are calculated with the above second order multireference perturbation theory (MRPT2). Different basis sets with varieties of levels of theoretical methods have been exploited to calculate the electron affinity in literature. In order to compare the performance of different methods conveniently, the system basis sets, Dunning's correlation consistent basis functions,57,58ccpVDZ, cc-pVTZ, aug-cc-pVDZ, and aug-cc-pVTZ are used for all theoretical approaches in the present work. CASSCF wave function is chosen as the zeroth order wavefucntion in MRPT2 and is calculated with GAMESS.59CAS(N,M) means that the configuration space is constructed with N electrons distributed among M orbitals in all possible ways. Calculations with CCSD, CCSD(T), B3LYP, X3LYP, M06, HTCH, TPSS, B97D3, mPW2PLYP, and B2PLYP are carried out with Gaussian program.60Calculations with CASPT2 are carried out with MOLPRO.61

3 Results and discussion

3.1 Electron affinities of F and Cl

There are many theoretical works on the electron affinity (EA) of F. Here only some representative works are discussed. They are the fourth order Møller-Plesset perturbation theory (MP4) and the coupled cluster theory,62Gaussian-1 theory,63Gaussian-2 theory,65BLYP density functional theory,66one electron propagator,67,68and the multireference coupled cluster theory.69In comparison with the EA value of 3.65 eV calculated with MP4,62the coupled cluster result (3.37 eV) is much close to the experimental result of 3.401 eV.64The theoretical estimation of Pople et al.65for the affinity agrees perfectly with experiment, but has been obtained by assuming the additivity of the energy contributions arising from different basis set extensions, which introduces an approximation. The EA values (3.550 eV67and 3.538 eV68) calculated with one electron propagator theories are overestimated. The results calculated with the multireference coupled cluster theory at the basis level of aug-cc-pVDZ, aug-cc-pVTZ, and aug-cc-pVQZ are 3.2378, 3.4014, and 3.4986 eV, respectively.69These results are presented at the bottom of Table 1 for the convenience of comparison.

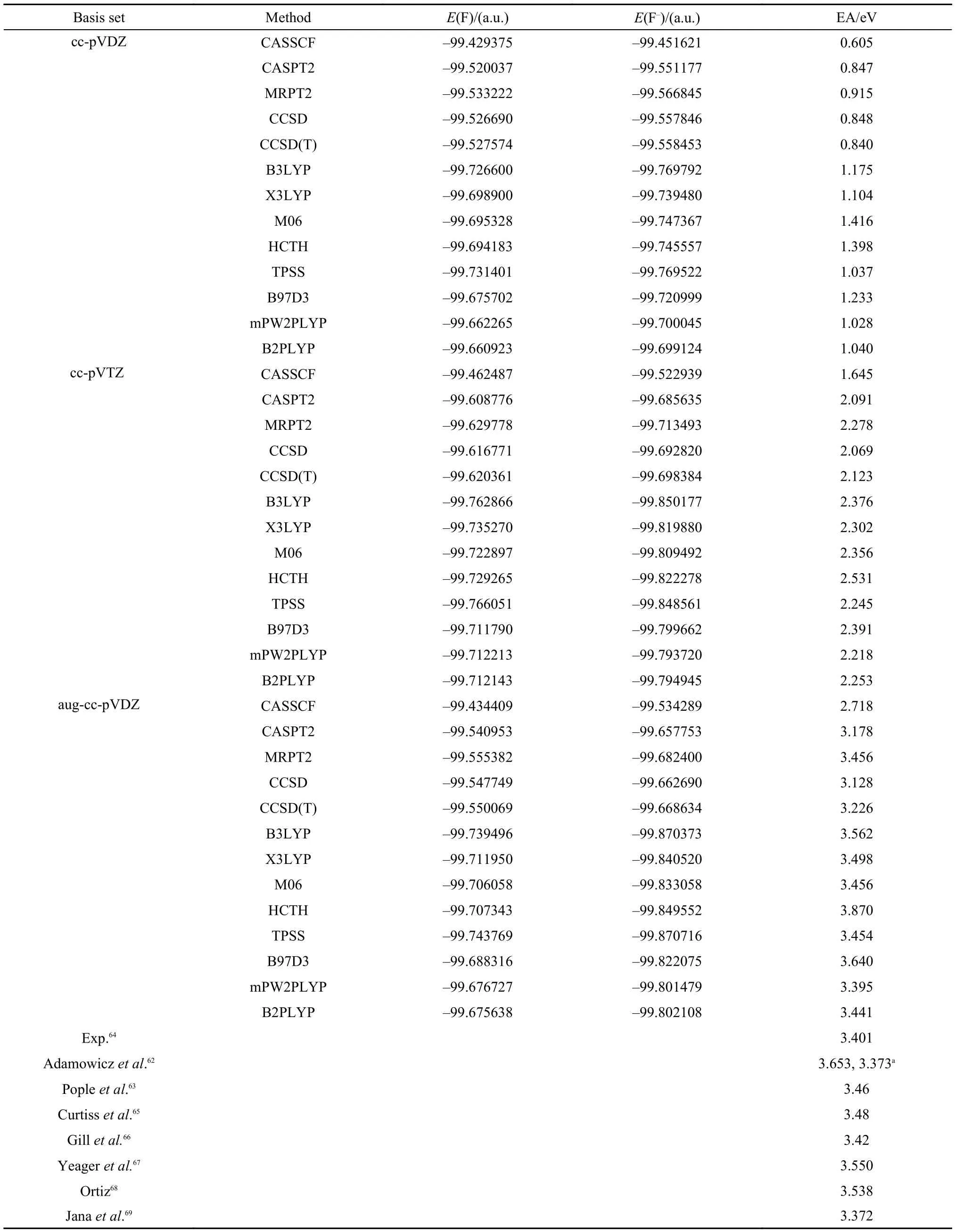
Table1 Electron affinities (EA) of F calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP, and B2PLYP methods

In this study, the complete active spaces for F and F–are CAS(5,7) and CAS(6,7), respectively. The electron affinities calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HTCH, TPSS, B97D3, mPW2PLYP, and B2PLYP are listed in Table 1. As can be seen from the table, the EA values calculated with the cc-pVDZ basis set are far away from the experimental value of 3.401 eV64in spite of various theoretical methods used. As the basis set is increased to cc-pVTZ, the number of the bases is changed from 14 to 30. Yet the computed EAs are still not so close to the experimental value although they are improved substantially. However, when aug-cc-pVDZ is considered, the theoretical EA values computed with MRPT2, CCSD, CCSD(T), and CASPT2 become much closer to the experimental result in spite of the fact that the number of the bases in the aug-cc-pVDZ is less than the number of the bases in the cc-pVTZ. This demonstrates the important role of diffuse functions in obtaining accurate theoretical EA values. Among the wavefunction methods, the best agreement with the experimental EA value of 3.401 eV64has been achieved by MRPT2/aug-cc-pVDZ with the difference less than 0.100 eV. CASPT2 results are less accurate than the results of MRPT2 and CCSD(T) but are slightly better than the results of CCSD for this problem at the level of aug-cc-pVDZ. However, all CASSCF results are not satisfactory and their differences with the experimental value of 3.401 eV64are still as large as about 0.700 eV even at the level of aug-cc-pVDZ. The accuracies of M06, TPSS, mPW2PLYP, and B2PLYP are comparable to the accuracy of MRPT2 and are better than the accuracies of B3LYP, X3LYP, HTCH, and B97D3. In comparison with the B3LYP results, Gill et al.66obtained an accurate EA value of 3.42 eV for F with BLYP/6-311+G(2df, p) as shown at the bottom of Table 1, but results of BLYP are not stable and case dependent. This is the nature of density functional theory as will be shown later.

Because of similarity of the valence electron structure between Cl and F, the complete active spaces for Cl and Cl–are also CAS(5,7) and CAS(6,7), the same as for F and F–, respectively. The calculated electron affinities of Cl with various methods are listed in Table 2. It can be seen from the table that the best EA value is 3.601 eV obtained with MRPT2/aug-ccpVDZ, which is comparable to the accuracy achieved with the renormalized electron propagator method at the level of aug-ccpVTZ by Ortiz68as shown at the bottom of the table. The EA value of 3.617 eV with a model potential-quantum Monte Carlo study70is in very good agreement with experiment,71yet its error is as high as ±0.198 eV because of stochastic nature of Monte Carlo method. Among the density functional theories, the accuracies of mPW2PLYP and B2PLYP are comparable to the accuracy of MRPT2. Their performances are better than that of CCSD, CCSD(T), CASPT2, and other density functional methods presented in Table 2. The accuracy of CASSCF results at different levels of basis sets are still inferior to the accuracies of other methods listed in the table indicating the important role played by the dynamic correlation.

3.2 Electron affinities of OH and SH

The experimental equilibrium bond lengths of OH and OH–72are used for electron affinity calculation. OH is an isoelectronic system of F. However, its electronic structure seems more complicated than the latter. We first explore the complete active space CAS(5,6) and CAS(6,6) for OH and OH–separately. As shown at the top of Table 3, except the positive EA value calculated with MRPT2/cc-pVDZ, all other methods, CASSCF, CASPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HTCH, TPSS, B97D3, mPW2PLYP, and B2PLYP at the same basis, predict negative EA values indicating that OH–is not stable, which is however not in agreement with the experimental observation.73Furthermore, CASSCF wavefunction at cc-pVTZ basis still produces a negative EA value. These calculations demonstrate the difficulty in obtaining the electron affinity of OH. As the basis set is extended to aug-cc-pVDZ, EAs calculated with various methods except CASSCF are improved substantially. However, the CASPT2, CCSD, and CCSD(T) results still underestimate the experimental value while the MRPT2 result overestimates it. As the basis is extended further to aug-cc-pVTZ, the EAs calculated with CASPT2, CCSD, and CCSD(T) are improved as shown in the lower part of Table 3. However, the change of the basis set almost has no effect on the results of CASSCF and MRPT2, which means that a large static correlation may be needed for a further improvement on their EA values. Therefore, the complete active spaces are enlarged from CAS(5,6) and CAS(6,6) to CAS(7,7) and CAS(8,7) for OH and OH–, respectively. The corresponding results are listed at the lower part of Table 3. The MRPT2 result of 1.91 eV becomes better than the result of 2.044 eV obtained with a small complete active space and agrees very well with the experimental value of 1.83 eV73to within 0.10 eV. However, the CASSCF and CASPT2 results are still not satisfactory. The EA value of 1.78 eV calculated with MP4 and a large basis 6-311++G(3df, 3pd) is reported by Frenking and Koch75and are in very good agreement with the experimental value of 1.83 eV. Though partial quadruple excitations in MP4 have been included in CASPT2, yet it seems that these excitations are still not enough to achieve an accurate result with CASPT2.

Among the density functional methods, the results of B3LYP, X3LYP, B97D3, mPW2PLYP, and B2PLYP at the level of aug-cc-pVTZ are in very close agreement with the experimental value of 1.83 eV.73Similar results of other density function theories like BLYP66,74are listed at the bottom of Table 3.65–68,73–75As can be seen from the results of Tables 1–3, density functional theories as a whole are reliable approaches at a very large basis set though the performance of each individual functional is different from each other and is dependent on the system studied.

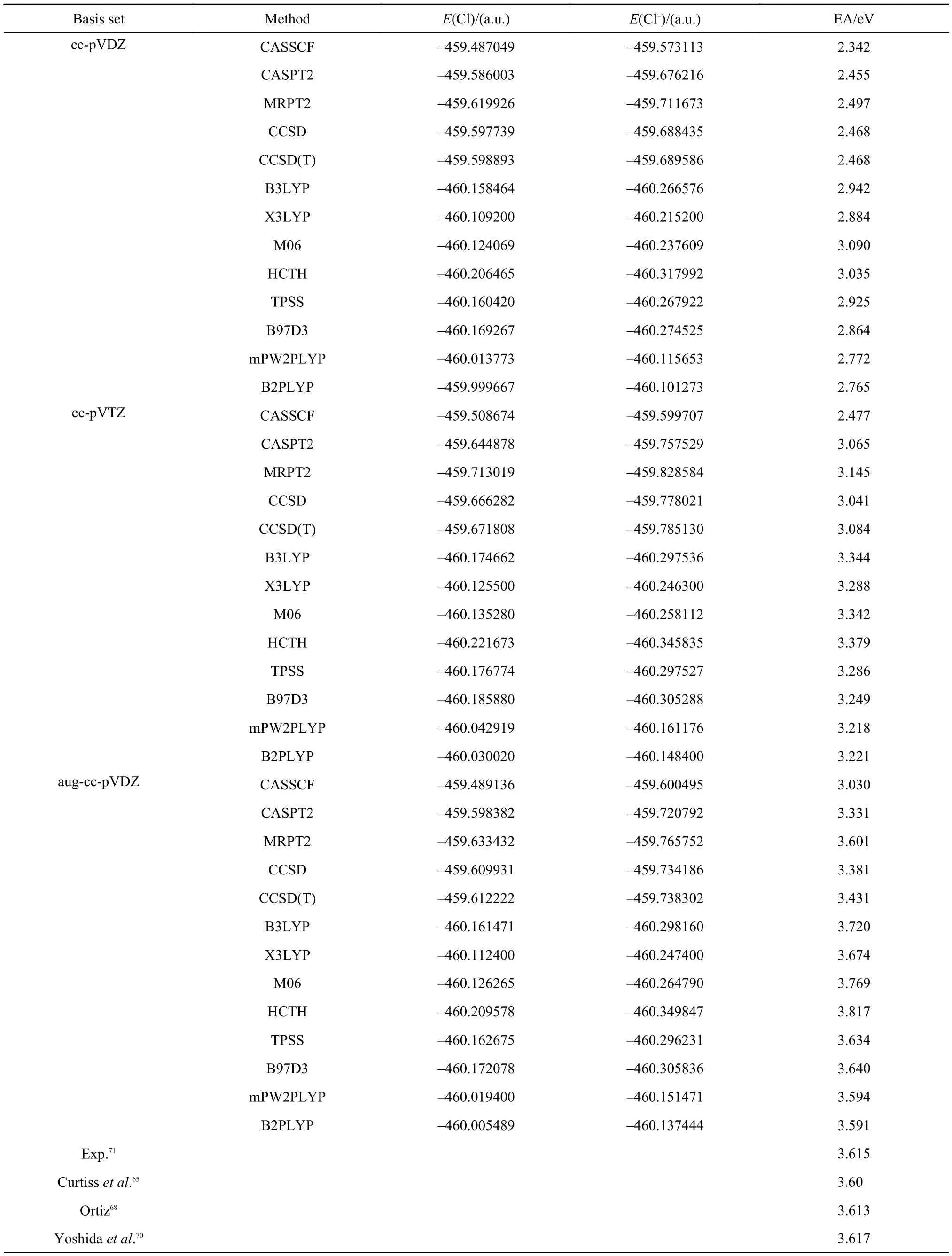
Table2 Electron affinities of Cl calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP, and B2PLYP methods

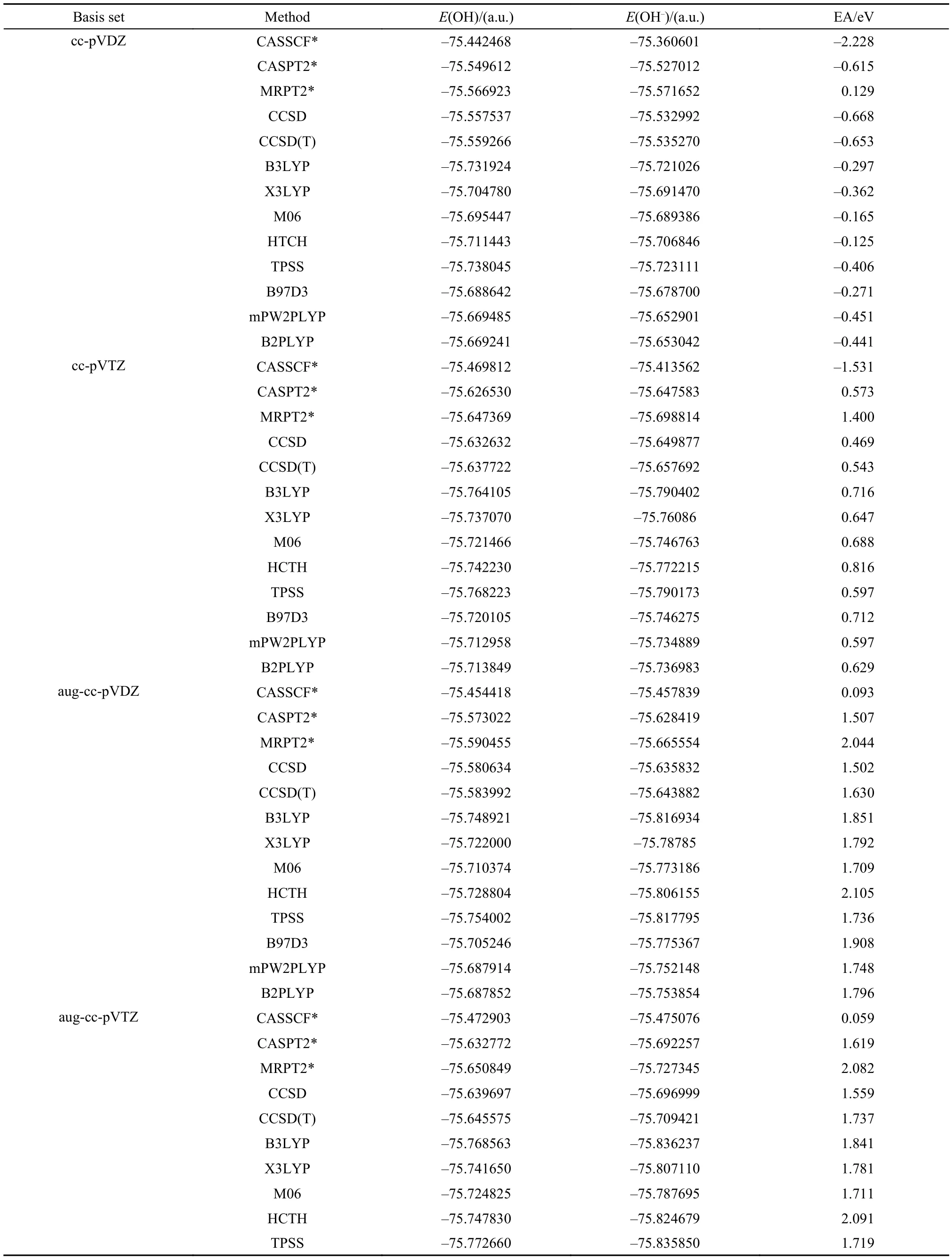
Table3 Electron affinities of OH calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP, and B2PLYP methods

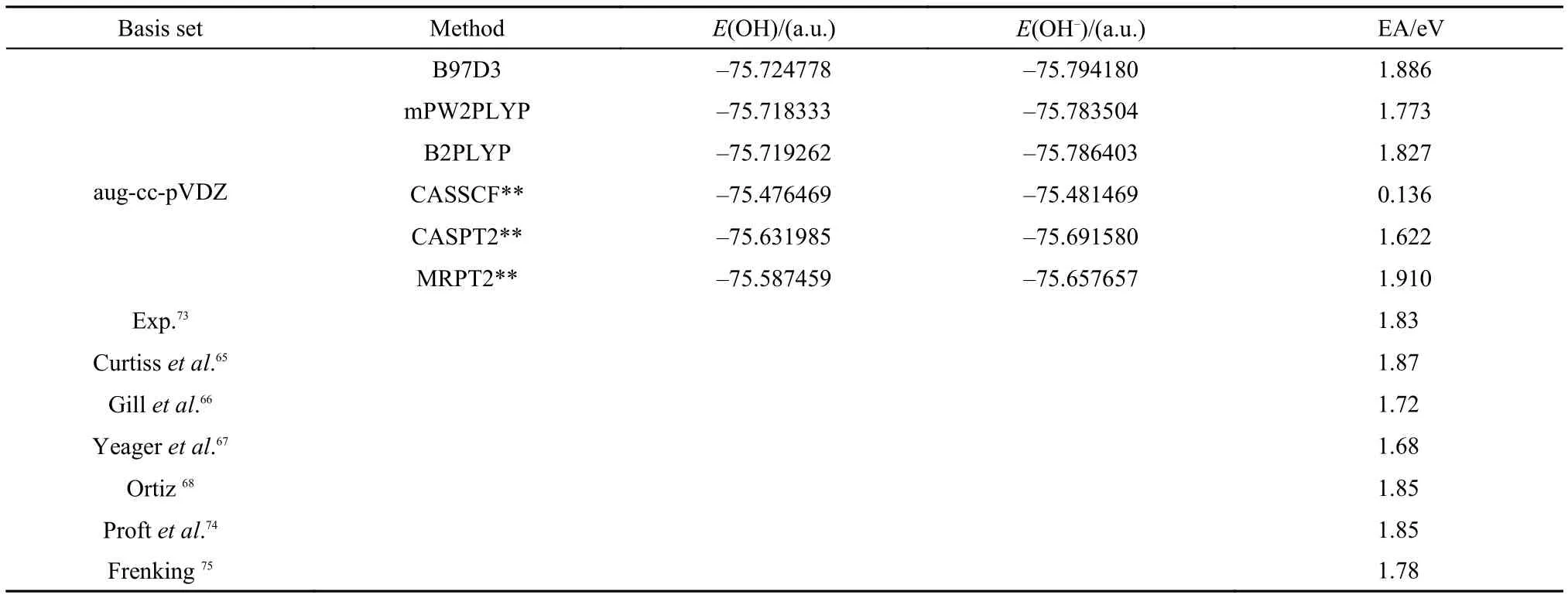
continued Table 3

The bond lengths of SH and SH–are 0.1338 and 0.1342 nm,68respectively. They are optimized with the second-order Møller-Plesset perturbation theory at the level of 6-311++G(d,p) basis. Electron affinities of SH calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HTCH, TPSS, B97D3, mPW2PLYP, and B2PLYP are presented in Table 4. In comparison with the results of OH in Table 3, EAs of SH are all positive at the level of cc-pVDZ basis, which indicates that EAs of SH are easier to be calculated. At the level of aug-cc-pVDZ, the results of MRPT2, B3LYP, X3LYP, M06, TPSS, B97D3, mPW2PLYP, and B2PLYP are very close to the experimental value of 2.319 eV.76As the basis set is extended to aug-cc-pVTZ, the CCSD(T) result is also improved and is in close agreement with the experimental result. But the CASPT2 and CCSD results are still about 0.2 eV less than the experimental value. The performance of CASSCF even with the augcc-pVTZ basis is still much inferior to the performances of all other methods listed in the table.

3.3 Electron affinity of CN

The experimental equilibrium bond lengths of CN and CN–are separately 0.1172 and 0.1177 nm72and are exploited for computation of the electron affinity. The complete active spaces for CN and CN–are CAS(7,7) and CAS(8,7), respectively. The results calculated with various theoretical methods are presented in Table 5. In comparison with the experimental EA value of 3.82 eV,77the performances of MRPT2, HCTH, M06, and B2PLYP with aug-cc-pVDZ are better than those of other theoretical approaches presented in the table.

The previous studies on the electron affinity of CN are listed at the bottom of the table for the purpose of comparison. Among them, the results of Gaussian-2 theory by Pople et al.65and one electron propagator method by Ortiz68are very close to the experimental value of 3.82 eV.77However, the BLYP density functional theory result by Gill et al.66is inferior to the BLYP result by Proft and Geerlings74due to their different basis sets used in the study. The EA value predicted by Yeager et al.67with the electron propagator method is also not satisfactory.

3.4 Electron affinities of CH2and NH2

The geometrical parameters of CH2,NH2, andare taken from references,68,78respectively. Electron affinities of CH2and NH2are presented in Tables 6 and 7.65–68,74,78–82As can be seen from these two tables, most of EA values of CH2and NH2are negative at the basis levels of cc-pVDZ and cc-pVTZ. Even though the EAs of CH2calculated with MRPT2 and density functional methods at the level of cc-pVTZ are positive, yet their absolute errors with the experimental value of 0.652 eV79are still large. These results demonstrate that CH2and NH2are more difficult to describe than OH as discussed in Section 3.2. As the basis is extended to aug-cc-pVDZ, the EAs of CH2calculated with all theoretical approaches are improved substantially and are listed in the lower part of Table 6. The MRPT2 result of CH2is in very close agreement with the experimental value with the absolute error less than 0.04 eV.79On the other hand, the EA of NH2calculated with MRPT2/aug-cc-pVDZ is still not satisfactory, which is similar to the situation of OH in Table 3. Therefore, the complete active spaces of NH2andare enlarged from CAS(6,6) and CAS(7,6) to CAS(7,7) and CAS(8,7), respectively. As can be seen from Table 7, the effect of the size of the complete active space on EA values is very significant. The absolute error of the MRPT2 result is only 0.005 eV in comparison with the experimental value of 0.77eV.81The performances of CASSCF and CASPT2 are still not satisfactory.

Similar to the results of OH in Table 3, B3LYP, X3LYP, and B97D3 demonstrate very good performances for both CH2and NH2. The EA values of CH2calculated with HCTH, mPW2PLYP, and B2PLYP at the level of aug-cc-pVDZ is also in good agreement with the experimental result.79It is worthy to mention that good accuracies have been achieved with Gaussian-2 theory65, density functional theory,66,74one electron propagator method,68and the multireference configuration interaction method,80,82as listed at the bottoms of Tables 6 and 7.are CAS (6,6) and CAS(7,6), respectively.

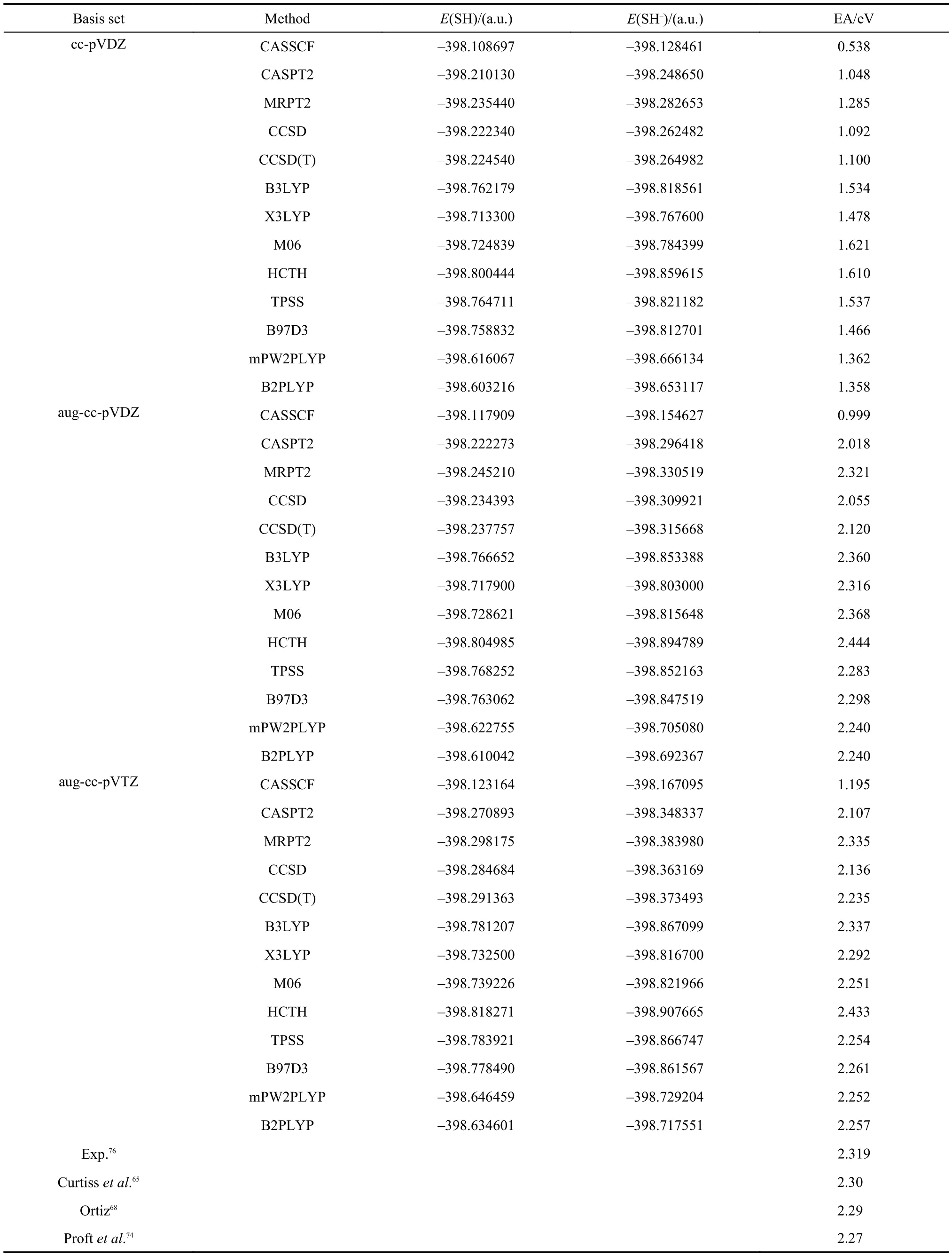
Table4 Electron affinities of SH calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP, and B2PLYP methods

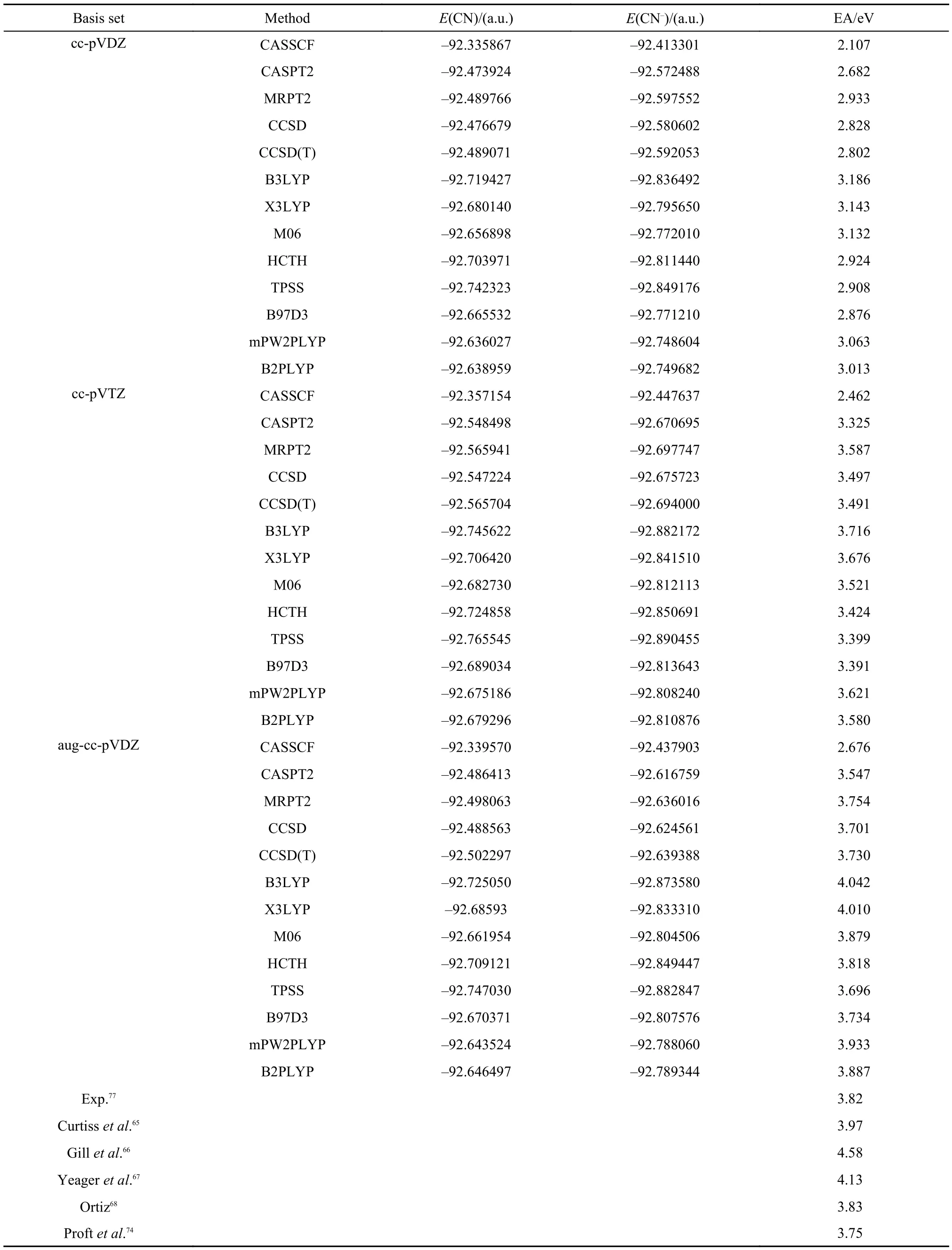
Table5 Electron affinity values for CN(X2Σ+) calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP, and B2PLYP methods

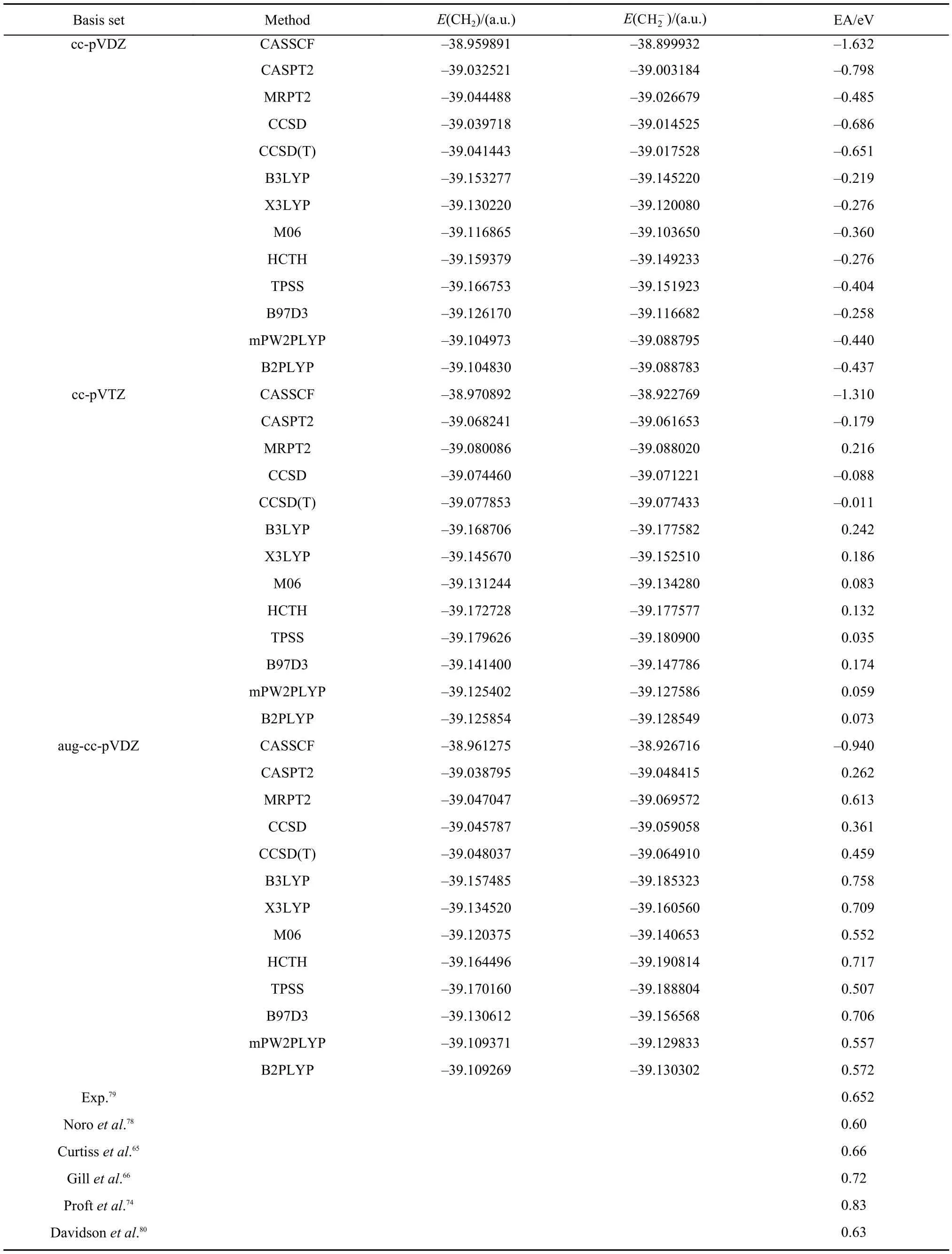
Table6 Electron affinities for CH2(X3B1) calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP, and B2PLYP methods

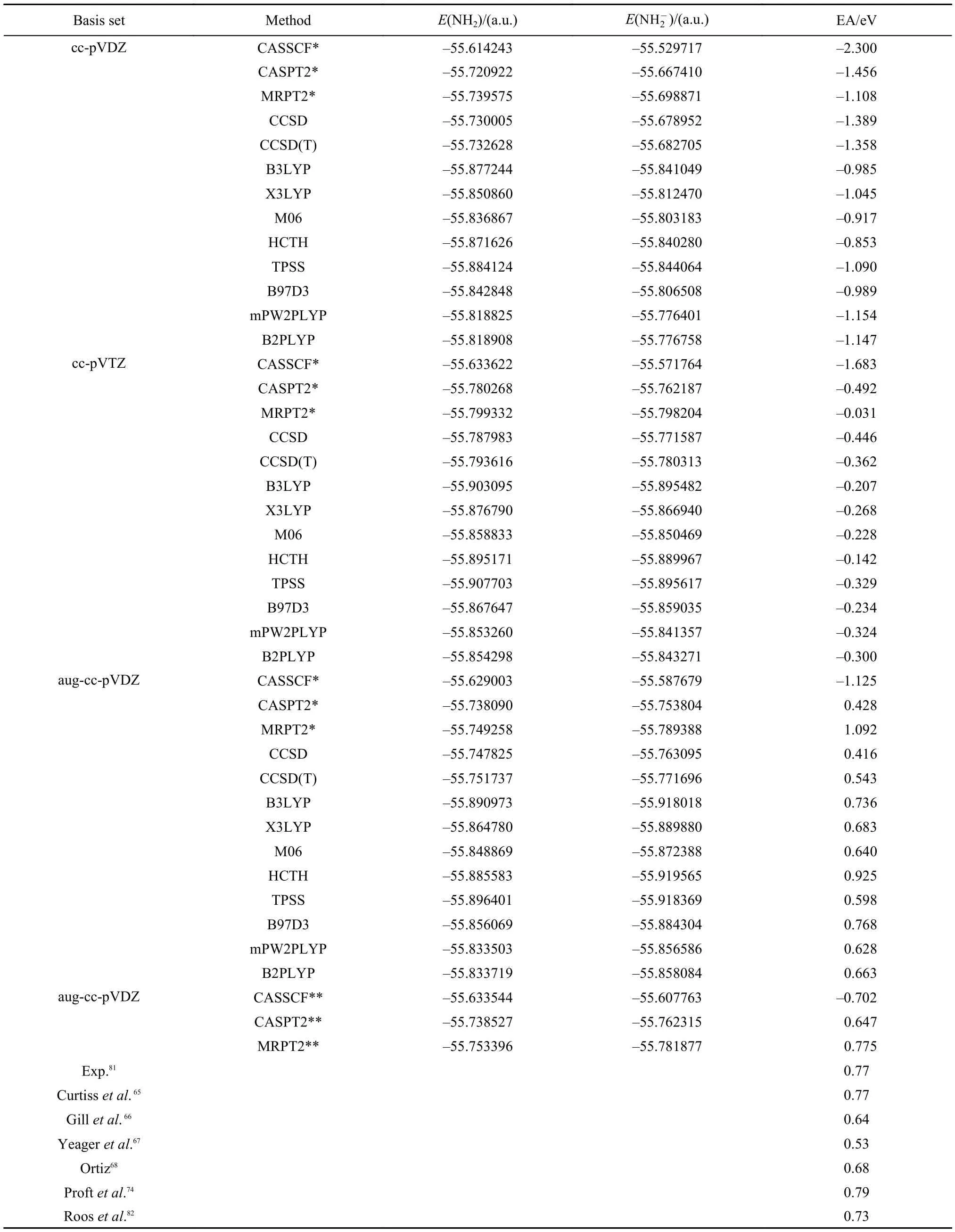
Table7 Electron affinities for NH2(X2B1) calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP, and B2PLYP methods

4 Conclusions

The electron affinities of F, Cl, OH, SH, CN, CH2, and NH2calculated with CASSCF, CASPT2, MRPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP, and B2PLYP are presented in this study at four levels of basis sets, cc-pVDZ, cc-pVTZ, aug-cc-pVDZ, and aug-cc-pVTZ. MRPT2 results are in very close agreement with the experimental results to within 0.1 eV. Its overall performance is the best among these methods. Density functional theories as a whole are reliable approaches at the aug-cc-pVDZ level though the performance of each individual functional is dependent on the system studied. The performance of CASSCF is inferior to all other methods tested in this study. The wrong sign of the electron affinities of CH2and NH2calculated with CASSCF even at aug-cc-pVDZ level indicates that CASSCF wavefunction may be not a reliable choice at least for the systems studied here.

It is shown in this work that the diffuse functions play an important role in achieving an accurate result. On the other hand, it is also seen from the results of OH and NH2that a relatively large size of the complete active space has a significant effect on the accuracy of the results of MRPT2 since it will introduce higher level of excitation configurations into the zeroth order wavefunction as well as the perturbation wavefunction.

(1)Chen, F. W. Computaional Method in Quantum Chemistry; Science Press: Beijing, 2008; pp 70–72. [陈飞武. 量子化学中的计算方法. 北京: 科学出版社, 2008: 70–72.]

(2)Feng, X. J.; Li, Q. S. Acta Phys. -Chim. Sin. 2004, 20, 1172. [封学军, 李前树. 物理化学学报, 2004, 20, 1172.] doi: 10.3866/PKU.WHXB20040923

(3)Huang, J. G.; Shi, T. Q.; Luo, Q. Y. Acta Chim. Sin. 2004, 62, 236. [黄俭根, 施踏青, 罗秋艳. 化学学报, 2004, 62, 236.]

(4)Li, H. X.; Tang, H. A.; Yang, S.; Xiao, T. Acta Phys. -Chim. Sin. 2007, 23, 1781. [李会学, 唐惠安, 杨 声, 萧 泰. 物理化学学报, 2007, 23, 1781.] doi: 10.3866/PKU.WHXB20071124

(5)Ding, X. L.; Wu, J. M.; Xu, X. Chem. J. Chin. Univ. 2008, 29, 396. [丁秀丽, 吴剑鸣, 徐 昕. 高等学校化学学报, 2008, 29, 396.]

(6)Peach, M. J. G.; Proft, F. D.; Tozer, D. J. J. Phys. Chem. Lett. 2010, 1, 2826. doi: 10.1021/jz101052q

(7)Li, W. W.; Hou, R. B.; Sun, Y. L. Acta Phys. -Chim. Sin. 2010, 26, 2772. [李伟伟, 侯若冰, 孙彦丽. 物理化学学报, 2010, 26, 2772.] doi: 10.3866/PKU.WHXB20101004

(8)Borgoo, A.; Tozer, D. J. J. Phys. Chem. A 2012, 116, 5497. doi: 10.1021/jp302801q

(9)Wei, M. J.; Jia, D. Q.; Chen, F. W. Acta Phys. -Chim. Sin. 2013, 29, 1441. [韦美菊, 贾德强, 陈飞武. 物理化学学报, 2013, 29, 1441.] doi: 10.3866/PKU.WHXB201304221

(10)Fu, R.; Lu, T.; Chen, F. W. Acta Phys. -Chim. Sin. 2014, 30, 628. [付 蓉, 卢 天, 陈飞武. 物理化学学报, 2014, 30, 628.] doi: 10.3866/PKU.WHXB201401211

(11)Cave, R. J.; Davidson, E. R. J. Chem. Phys. 1988, 88, 5770. doi: 10.1063/1.454535

(12)Andersson, K.; Malmqvist, P. A.; Roos, B. O. J. Chem. Phys. 1992, 96, 1218. doi: 10.1063/1.462209

(13)Hirao, K. Chem. Phys. Lett. 1992, 190, 374. doi: 10.1016/0009-2614(92)85354-D

(14)Hirao, K. Chem. Phys. Lett. 1992, 196, 397. doi: 10.1016/0009-2614(92)85710-R

(15)Kozlowski, P. W.; Davidson, E. R. J. Chem. Phys. 1994, 100, 3672. doi: 10.1063/1.466355

(16)Kozlowski, P. W.; Davidson, E. R. Chem. Phys. Lett. 1994, 226, 440. doi: 10.1016/0009-2614(94)00763-2

(17)Hoffmann, M. R. J. Phys. Chem. 1996, 100, 6125. doi: 10.1021/jp952753r

(18)Mahapatra, U. S.; Datta, B.; Mukherjee, D. J. Phys. Chem . A 1999, 103, 1822. doi: 10.1021/jp9832995

(19)Khait, Y. G.; Song, J.; Hoffmann, M. R. J. Chem. Phys. 2002, 117, 4133. doi: 10.1063/1.1497642

(20)Wang, Y. B.; Gang, Z. T.; Su, K. H.; Wen, Z. Y. Scientia Sinica Chimica 2000, 30, 543. [王育彬, 甘正汀, 苏克和, 文振翼. 中国科学: 化学, 2000, 30, 543.]

(21)Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J. P. J. Chem. Phys. 2001, 114, 10252. doi: 10.1063/1.1361246

(22)Angeli, C.; Bories, B.; Cavallini, A.; Cimiraglia, R. J. Chem. Phys. 2006, 124, 054108. doi: 10.1063/1.2148946

(23)Chen, F.; Davidson, E. R.; Iwata, S. Int. J. Quantum Chem. 2002, 86, 256. doi: 10.1002/qua.1105

(24)Rolik, Z.; Szabados, Á.; Surján, P. R. J. Chem. Phys. 2003, 119, 1922. doi: 10.1063/1.1584424

(25)Szabados, A.; Rolik, Z.; Tóth, G.; Surján, P. R. J. Chem. Phys. 2005, 122, 114104. doi: 10.1063/1.1862235

(26)Chen, F. Sci. China-Chem. 2007, 50, 483. doi: 10.1007/s11426-007-0074-0

(27)Chen, F. W. Acta Phys. -Chim. Sin. 2007, 23, 1360. [陈飞武. 物理化学学报, 2007, 23, 1360.] doi: 10.1016/S1872-1508(07)60072-2

(28)Fink, R. F. Chem. Phys. 2009, 356, 39. doi: 10.1016/j.chemphys. 2008.10.004

(29)Chen, Z.; Song, J.; Shaik, S.; Hiberty, P. C.; Wu, W. J. Phys. Chem. A 2009, 113, 11560.

(30)Chen, F. J. Chem. Theory Comput. 2009, 5, 931. doi: 10.1021/ct800546g

(31)Chen, F.; Wei, M.; Liu, W. Sci. China-Chem. 2011, 54, 446. doi: 10.1007/s11426-010-4199-1

(32)Kobayashi, M.; Szabados, Á.; Nakai, H.; Surján, P. R. J. Chem. Theory Comput. 2010, 6, 2024. doi: 10.1021/ct1001939

(33)Mao, S.; Cheng, L.; Liu, W.; Mukherjee, D. J. Chem. Phys. 2012, 136, 024105. doi: 10.1063/1.3672083

(34)Mao, S.; Cheng, L.; Liu, W.; Mukherjee, D. J. Chem. Phys. 2012, 136, 024106. doi: 10.1063/1.3672085

(35)Chen, Z.; Hoffmann, M. R. J. Chem. Phys. 2012, 137, 014108.doi: 10.1063/1.4731634

(36)Lei, Y.; Wang, Y.; Han, H.; Song, Q.; Suo, B.; Wen, Z. J. Chem. Phys. 2012, 137, 144102. doi: 10.1063/1.4757264

(37)Xu, E.; Li, S. J. Chem. Phys. 2013, 139, 174111. doi: 10.1063/1.4828739

(38)Chen, F.; Fan, Z. J. Comput. Chem. 2014, 135, 121.

(39)Liu, W.; Hoffmann, M. R. Theor. Chem. Acc. 2014, 133, 1481. doi: 10.1007/s00214-014-1481-x

(40)Chen, Z.; Chen, X.; Ying, F.; Gu, J.; Zhang, H.; Wu, W. J. Chem. Phys. 2014, 141, 134118. doi: 10.1063/1.4896534

(41)Roos, B.; Taylor, P.; Siebahn, P. Chem. Phys. 1980, 48, 157. doi: 10.1016/0301-0104(80)80045-0

(42)Cizek, J. Adv. Chem. Phys. 1969, 14, 35.

(43)Purvis, G. D.; Bartlett, R. J. J. Chem. Phys. 1982, 76, 1910. doi: 10.1063/1.443164

(44)Scuseria, G. E.; Janssen, C. L.; Schaefer, H. F., III. J. Chem. Phys. 1988, 89, 7382. doi: 10.1063/1.455269

(45)Scuseria, G. E.; Schaefer, H. F., III. J. Chem. Phys. 1989, 90, 3700. doi: 10.1063/1.455827

(46)Pople, J. A.; Head-Gordon, M.; Raghavachari, K. J. Chem. Phys. 1987, 87, 5968. doi: 10.1063/1.453520

(47)Becke, A. D. Phys. Rev. A 1988, 38, 3098.

(48)Beck, A. D. J. Chem. Phys. 1993, 98, 5648.

(49)Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785.

(50)Xu, X.; Goddard, W. A., III. Proc. Natl. Acad. Sci. U. S. A. 2004, 101, 2673. doi: 10.1073/pnas.0308730100

(51)Zhao, Y.; Truhlar, D. G. Theor. Chem. Acc. 2008, 120, 215.

(52)Hamprecht, F. A.; Cohen, A. J.; Tozer, D. J.; Handy, N. C. J. Chem. Phys. 1998, 109, 6264. doi: 10.1063/1.477267

(53)Tao, J.; Perdew, J.; Staroverov, V.; Scuseria, G. Phys. Rev. Lett. 2003, 91, 146401. doi: 10.1103/PhysRevLett.91.146401

(54)Grimme, S.; Ehrlich, S.; Goerigk, L. J. Comp. Chem. 2006, 27, 1787. doi: 10.1002/jcc.20495

(55)Grimme, S. J. Chem. Phys. 2006, 124, 034108. doi: 10.1063/1.2148954

(56)Schwabe, T.; Grimme, S. Phys. Chem. Chem. Phys. 2006, 8, 4398. doi: 10.1039/b608478h

(57)Dunning, T. H. J. Chem. Phys. 1989, 90, 1007. doi: 10.1063/1.456153

(58)Woon, D. E.; Dunning, T. H. J. Chem. Phys. 1993, 98, 1358. doi: 10.1063/1.464303

(59)Schmidt, M. W.; Baldridge, K. K.; Boatz, J. A.; Elbert, S. T.; Gordon, M. S.; Jensen, J. H.; Koseki, S.; Natsunaga, N.; Nguyen, K. A.; Su, S. J.; Windus, T. L.; Dupuis, M.; Montgomery, J. A. J. Comput. Chem. 1993, 14, 1347.

(60)Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; et al. Gaussian 09W, Revision D.01; Gaussian Inc.: Pittsburgh, PA, 2009.

(61)Werner, H. J.; Knowles, P. J.; Lindh, R.; MAnby, F. R.; Schütz, M. et al. Molpro, 2009.1 , a Package of ab initio Programs; See http://www.molpro.net.

(62)Adamowicz, L.; Bartlett, R. J. Chem. Phys. 1986, 84, 6837. doi: 10.1063/1.450688

(63)Pople, J. A.; Head-Gordon, M.; Fox, D. J.; Raghavachari, K.; Curtiss, L. A. J. Chem. Phys. 1989, 90, 5622. doi: 10.1063/1.456415

(64)Blondel, C.; Cacciani, P.; Delsart, C.; Trainham, R. Phys. Rev. A 1989, 40, 3698. doi: 10.1103/PhysRevA.40.3698

(65)Curtiss, L. A.; Raghavachari, K.; Trucks, G. W.; Trucks, G. W.; Pople, J. A. J. Chem. Phys. 1991, 94, 7221. doi: 10.1063/ 1.460205

(66)Gill, P. M. W.; Johnson, B. G.; Pople, J. A.; Frisch, M. J. Chem. Phys. Lett. 1992, 197, 499. doi: 10.1016/0009-2614(92)85807-M

(67)Yeager, D. L.; Nichols, J. A.; Golab, J. T. J. Chem. Phys. 1992, 97, 8441. doi: 10.1063/1.463414

(68)Ortiz, J. V. Chem. Phys. Lett. 1998, 296, 494. doi: 10.1016/S0009-2614(98)01067-7

(69)Jana, D.; Datta, D.; Mukherjee, D. Chem. Phys. 2006, 329, 290. doi: 10.1016/j.chemphys.2006.08.025

(70)Yoshida, T.; Mizushima, Y.; Iguchi, K. J. Chem. Phys. 1988, 89, 5815. doi: 10.1063/1.455557

(71)Hotop, H.; Lineberger, W. C. J. Phys. Chem. Ref. Data 1975, 4, 539. doi: 10.1063/1.555524

(72)Huber, K. P.; Herzberg, G. Molecular Spectra and Molecular Structure IV: Constants of Diatomic Molecules; Van Nostrand Reinhold: New York, 1979.

(73)Schulz, P. A.; Mead, R. D.; Jones, P. L.; Linebergert W. C. J. Chem. Phys. 1982, 77, 1153. doi: 10.1063/1.443980

(74)Proft, F. D.; Geerlings, P. J. Chem. Phys. 1997, 106, 3270. doi: 10.1063/1.473796

(75)Frenking, G.; Koch, W. J. Chem. Phys. 1986, 84, 3224. doi: 10.1063/1.450832

(76)Steiner, B. J. Chem. Phys. 1968, 49, 5097. doi: 10.1063/1.1670004

(77)Berkowitz, J.; Chupka W. A.; Walter, T. A. J. Chem. Phys. 1969, 50, 1497. doi: 10.1063/1.1671233

(78)Noro, T.; Yoshimine, M. J. Chem. Phys. 1989, 91, 3012. doi: 10.1063/1.456922

(79)Leopold, D. G.; Murray, K. K.; Stevens-Miller, A. E.; Lineberge, W. C. J. Chem. Phys. 1985, 83, 4849. doi: 10.1063/1.449746

(80)Feller, D.; McMurchie, L. E.; Borden, W. T.; Davidson, E. R. J. Chem. Phys. 1982, 77, 6134. doi: 10.1063/1.443858

(81)Wickham-Jones, C. T.; Ervin, K. M.; Ellison, G. B.; Lineberge, W. C. J. Chem. Phys. 1989, 91, 2762. doi: 10.1063/1.456994

(82)Merchan, M.; Roos, B. O. Chem. Phys. Lett. 1991, 184, 346. doi: 10.1016/0009-2614(91)85135-J

Computation of Electron Affinities with the Second Order Multireference Perturbation Theory

FAN Zhi-Hui CHEN Fei-Wu*
(Department of Chemistry and Chemical Engineering, School of Chemistry and Biological Engineering, University of Science and Technology Beijing; Beijing Key Laboratory for Science and Application of Functional Molecular and Crystalline Materials, Beijing 100083, P. R. China)

Electron affinities of F, Cl, OH, SH, CN, CH2, and NH2have been computed with the second order multireference perturbation theory. The effects of basis set and size of the complete active space on accuracy of electron affinity have also been investigated. The results are compared with calculations performed with CASSCF, CASPT2, CCSD, CCSD(T), B3LYP, X3LYP, M06, HCTH, TPSS, B97D3, mPW2PLYP, and B2PLYP. The overall performance of the second order multireference perturbation theory is best at the level of basis sets used in this study.

Electron affinity; Multireference perturbation theory; Basis set; Complete active space

O641

10.3866/PKU.WHXB201508201

Received: June 1, 2015; Revised: August 12, 2015; Published on Web: August 20, 2015.

*Corresponding author. Email: chenfeiwu@ustb.edu.cn; Tel: +86-10-62332689.

The project was supported by the National Natural Science Foundation of China (21173020, 21473008).

国家自然科学基金(21173020, 21473008)资助项目

© Editorial office of Acta Physico-Chimica Sinica