卜月华， 鲍旭东

(浙江师范大学数理与信息工程学院，浙江金华 321004)

没有7－圈的平面图的BB－染色*

卜月华， 鲍旭东

(浙江师范大学数理与信息工程学院，浙江金华 321004)

研究了没有7－圈的连通平面图的BB－染色问题.应用经典的Discharging方法，证明了没有7－圈且不含相邻4－圈的连通平面图G，存在G的一棵生成树T，使得(G，T)是BB－4－可染的.这一结果进一步拓展了平面图的BB－4－可染的充分条件.

平面图;BB－染色;生成树;圈

0 引言

本文只考虑有限无向简单图.对于平面图G，用V(G)，E(G)，F(G)，Δ(G)和δ(G)表示图G的顶点集、边集、面集、最大度和最小度.称平面图G的度数为k(至多为k，至少为k)的顶点为k－点(k－－点，k+－点).对于平面图，可类似地定义k－面、k－－面、k+－面.若2个面或者2个圈至少有一条公共边，则称这2个面或者2个圈相邻;若2个面或者2个圈有一个公共点，则称这2个面或者2个圈相交.特别地，称3－圈为三角形.对于平面图G，若δ(G)≥2，则k(k≤5)－面均为简单面.本文未定义的符号和说明参见文献［1］.

设G=(V，E)是一个简单图，C是一个颜色集合，则称从V到C的一个映射φ:V→C为G的一个顶点染色.又若相邻的顶点染有不同的颜色，即uv∈E，使得φ(u)≠φ(v)，则称φ为G的一个正常染色，简称染色.进一步，若|C|=k，则称φ为G的一个k－染色.若G有一个k－染色，则称G是k－可染的.称χ(G)=min{k|G是k－可染的}为G的色数.

近几年来，基于正常染色，许多学者提出了各式各样的染色模型，其中BB－染色就是基于频率分配问题，是由Akiyama等［2］提出来的.设H为G的一个生成子图，(G，H)的一个BB－k－染色是指一个映射φ:V(G)→{1，2，…，k}，满足:1)若uv∈E(H)，则|φ(u)－φ(v)|≥2;2)若uv∈ E(G)E(H)，则|φ(u)－φ(v)|≥1.(G，H)的BB－色数是指最小的整数k，使得(G，H)是BB－k－可染的，记为χb(G，H).

Broersma等［3］研究了图的色数与BB－色数之间的关系，证明了图的BB－色数至多为2χ(G)－1，并且这个上界是可以达到的.近几年来，关于BB－染色取得了一些突出的成果［4－5］.文献［6］提出了如下问题:对于任意含奇圈的连通平面图G，若G的围长g≥k，则存在G的一棵生成树T，使得χb(G，T)=4.设β为上述命题为真的最小正整数k，试确定β的值.文献［6］指出，4≤β≤10;文献［7－8］证明了:若连通平面图G没有5－圈或者没有4－圈，则存在G的一棵生成树T，使得χb(G，T)≤4;文献［9］证明了:若连通平面图G没有6－圈或者没有7－圈且不含相邻三角形，则存在G的一棵生成树T，使得χb(G，T)≤4.对于BB－染色，以下问题值得进一步探讨:

问题1 对于任意含有奇圈的连通平面图G，是否存在G的一棵生成树T，使得χb(G，T)=4?

问题2 对于连通平面图G，T为G的任意一棵生成树，由四色定理可知，χb(G，T)≤7，那么能否证明χb(G，T)≤6?

问题3 对于连通平面图G，T为G的任意一棵生成树，不利用四色定理，如何证明χb(G，T)≤7?本文主要证明了下面定理:

定理1 设G是一个没有7－圈且不含相邻4－圈的连通平面图，则存在G的一棵生成树T，使得χb(G，T)≤4.

1 定理1的证明

下面用反证法来证明定理1.假设平面图G=(V，E，F)是使σ(G)=|V|+|E|最小的一个反例，即G满足:1)G是一个没有7－圈且不含相邻4－圈的连通平面图，对于 G的任意一棵生成树 T，都有χb(G，T)≥5;2)对于顶点数与边数之和小于σ(G)的连通平面图G'，若G'没有7－圈且不含相邻4－圈，则存在G'的一棵生成树T'，有χb(G'，T')≤4.

下面根据G的极小性，给出G的几个结构性质和定义.

定义1 若一个4－点v关联2个3－面和1个4－面，且这2个3－面不相邻，则称此4－点为坏4－点，此4－面为坏4－面(如图1所示的f1)，与坏4－面不相邻且相交于顶点v的面称为好面(如图1所示的f2).

图1 坏4－点v，坏4－面f1，好面f2

图G具有以下结构性质:

性质1［8］图G不含1－点.

性质2［8］图G不含2－点.

性质3［8］图G不含3－点.

下面运用权转移方法完成定理1的证明.

先假设平面图G=(V，E，F)是2－连通的，则G的每个面的边界都是一个圈，G中每个顶点v关联d(v)个面.根据连通平面图的Euler公式|V|+|F|－|E|=2及度和公式，有

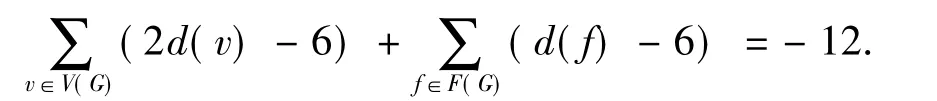
对于任意的x∈V(G)∪F(G)，构造一个权函数w(x)，其中当v∈V(G)时，w(v)=2d(v)－6，当f∈F(G)时，w(f)=d(f)－6，则

下面根据G的结构性质，在保持总的权和不变的情况下，对G中的点和面按照一定的权转移规则进行转权，经过权转移后得到一个新的权函数w'(x).将证明对于任意的x∈V(G)∪F(G)，都有w'(x)≥0，从而得到如下矛盾:

该矛盾说明反例G不存在，从而完成定理1的证明.

下面给出如下权转移规则:

R0:d(v)=4.

R0.1:若v不关联3－面，则v给关联的4+－面转权

R0.2:若v关联一个3－面，则v给关联的3－面转权1，给关联的4－面转权，给关联的5－面转权

R0.3:若v关联2个3－面，则v给关联的3－面转权1.

R1:d(v)=5.

R1.1:若v不关联3－面，则v给关联的4+－面转权

R1.2:若v关联1个3－面，则v给关联的3－面转权1，给关联的4－，5－面转权

R1.3:若v关联2个3－面，则v给关联的3－面转权1，给关联的4－面转权，给关联的5－面转权

下面证明∀v∈V(G)，w'(v)≥0.

1)d(v)=4或d(v)=5.

对于4－点v，由于图G不含7－圈且不含相邻的4－圈，则v最多关联2个3－面.若v不关联3－面，则由R0.1知，w'(v)≥2×4－6－1 2×4=0.若v仅关联1个3－面，则v最多再关联1个4－面或3个5－面，且v关联1个4－面时，v最多再关联1个5－面，进一步由R0.2知，

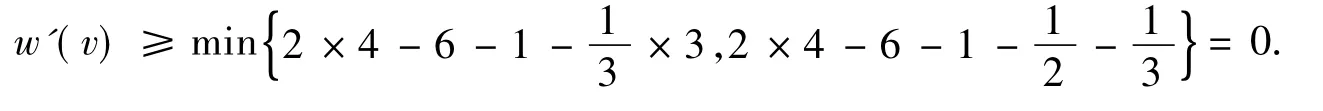
若v关联2个3－面，则v不再关联5－面且v最多再关联1个4－面，进一步由R0.3知，

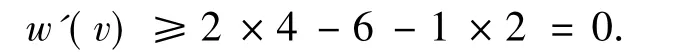
类似地，对于5－点v，由于图G不含7－圈且不含相邻的4－圈，则v最多关联3个3－面.若v不关联3－面，则由R1.1知，

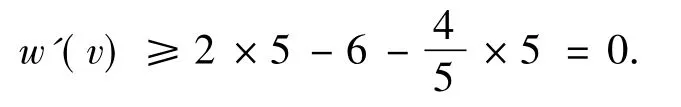
若v仅关联1个3－面，则v最多再关联2个4－面或4个5－面，且当v关联2个4－面时，v不再关联5－面，当v关联1个4－面时，v最多再关联2个5－面，进一步由R1.2知，

若v关联2个3－面，则v最多再关联1个4－面和2个5－面，进一步由R1.3知，

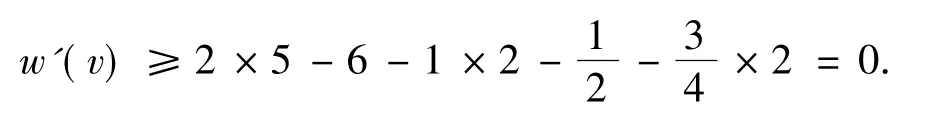
若v关联3个3－面，则v不再关联4－面和5－面，进一步由R1.4知，

2)d(v)=6，w(v)=6.

由于图G不含7－圈且不含相邻的4－圈，所以v最多关联4个3－面.若v关联4个3－面，则v不再关联4－面和5－面，进一步由R2知，

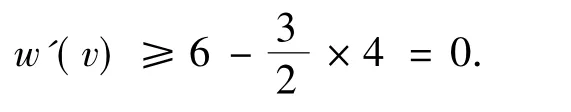
若v关联3个3－面，则v最多关联1个4－面或1个5－面，从而

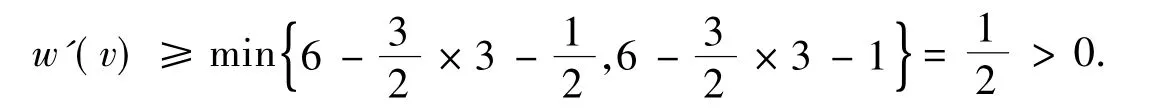
若v关联2个3－面，则v最多关联2个4－面或4个5－面，且当v关联2个4－面时，v不再关联5－面，从而

若v关联1个3－面，则v最多关联2个4－面或5个5－面，且当v关联2个4－面时，v最多再关联1个5－面，从而

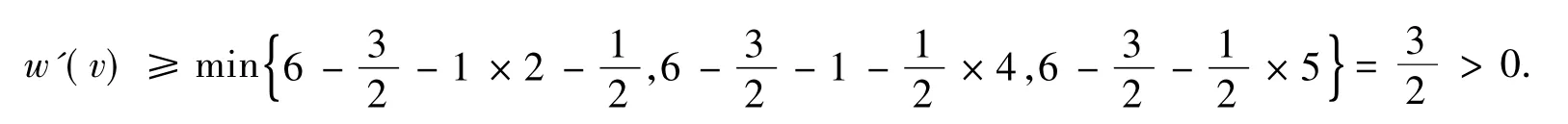
若v不关联3－面，则与v关联的都是4+－面，从而w'(v)≥6－1×6=0.

3)d(v)=7，w(v)=8.

由于图G不含7－圈且不含相邻的4－圈，所以v最多关联4个3－面.若v最多关联2个3－面，则由R2知，若v关联3个3－面，则v最多关联2个4－面，进一步由R2知，

若v关联4个3－面，则v最多关联1个4－面，且不再关联5－面，进一步由R2知，

4)d(v)=8，w(v)=10.

由于图G不含7－圈且不含相邻的4－圈，所以v最多关联5个3－面.若v最多关联4个3－面，则由R2知，.若v关联5个3－面，则v不再关联4－面或5－面，进一步由R2知，

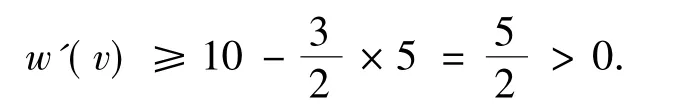
5)d(v)≥9，w(v)≥12.

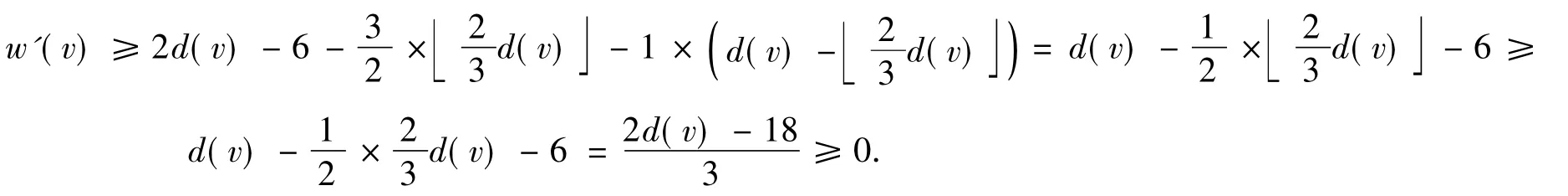
综上所述，即得∀v∈V(G)，w'(v)≥0.

下面证明∀f∈F(G)，w'(f)≥0.由于图G不含7－圈且不含相邻的4－圈及δ(G)≥4，可以得到如下断言:

断言1 4－面最多关联1个坏4－点.

断言2 好面为8+－面且好面最多关联个坏4－点.

1)d(f)=3，w(f)=－3.

由R0，R1和R2知，∀v∈V(G)，v给关联的3－面转权至少是1，则

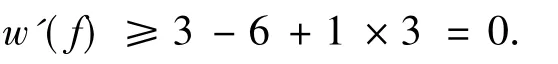
2)d(f)=4，w(f)=－2.

由于图G不含7－圈且不含相邻的4－圈，所以4－面最多关联2个3－面.若f不是坏4－面，则与f关联的4－点最多关联1个3－面，与f关联的5－点最多关联2个3－面，由R0，R1和R2知，与f关联的每个顶点v给f转权至少是，从而

若f是一个坏4－面，则由断言1、断言2和R3知，好面通过坏4－点给坏4－面转权至少是，而对于f中另外3个顶点中的每个顶点v，均不出现R0.3和R1.4的情形，故每个顶点v给f转权至少是，从而

3)d(f)=5，w(f)=－1.

由于图G不含7－圈且δ(G)≥4，所以f最多相邻1个3－面，f中至少有4个顶点不出现R0.3和R1.4的情形，则由R0，R1和R2知，f中的这些顶点v给关联的5－面转权至少是，从而

4)d(f)=6，w(f)=0.

由R0～R3知，6－面没有发生权转移，故w'(f)=w(f)=0.

5)d(f)≥8，w(f)≥2.

由断言2知，8+－面最多关联个坏4－点，由R3可得，

综上，当G是2－连通时，对每个x∈V(G)∪F(G)，w'(x)≥0.因此，

矛盾.

下面假设G不是2－连通的，这意味着G有割点.设B是一个仅包含1个割点ω的块，则B是2－连通的，且dB(ω)≥2.因此，B的每个面都是一个圈，B的每个顶点v关联dB(v)个不同的面.显然，B不含7－圈且不含相邻4－圈，因此B不含7－面且不含相邻4－圈.下面在B=(V(B)，E(B))中考虑权转移.设f0是B的外部面，则由性质1、性质2和性质3知，∀v∈V(B)－{ω}，dB(v)≥4.根据连通平面图的Euler公式|V|+|F|－|E|=2及度和公式，有

对于任意的x∈V(B)∪F(B)，构造一个权函数w(x)，其中当v∈V(B)时，w(v)=2dB(v)－6，当f∈F(B)时，w(f)=dB(f)－6.

在B中按以下规则进行权转移:

R4:顶点ω给每个除f0外的关联的3－，4－，5－面转权

R5:面f0通过坏4－点给坏4－面转权

R6:对于v∈V(B)－{ω}，f∈F(B)－{f0}，根据G是2－连通时的转权规则R0～R3进行.

容易发现，在完成R4～R6后，与前面一样可以验证:∀x∈V(B)∪F(B)－{ω，f0}，都有w'(x)≥0.下面考虑ω和f0，根据R4与dB(ω)≥2，有

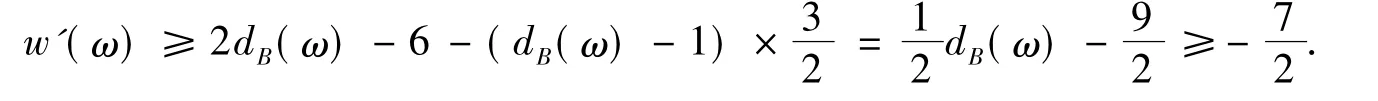
根据R5与dB(f0)≥3，有

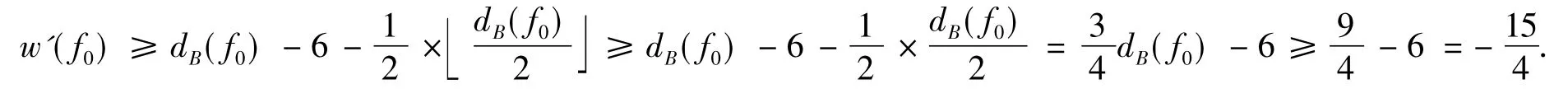
因此，

矛盾.定理1证毕.

2 结语

本文讨论了没有7－圈的连通平面图的BB－染色问题，证明了没有7－圈且不含相邻4－圈的连通平面图G，存在G的一棵生成树T，使得(G，T)是BB－4－可染的.那么，笔者认为，对于没有7－圈的连通平面图G，同样也存在G的一棵生成树T，使得(G，T)是BB－4－可染的.对此，笔者将作进一步的研究.

［1］Bondy J A，Murty U S R.Graph theory［M］.Berlin:Springer，2008.

［2］Akiyama J，Baskoro E T，Kano M.Combinatorial geometry and graph theory［M］.Berlin:Springer，2005:65－79.

［3］Broersma H，Fomin F V，Golovach P A，et al.Backbone coloring for graphs:tree and path backbone［J］.J Graph Theory，2007，55(2):137－152.

［4］Broersma H，Fujisawa J，Marchal L，et al.λ－backbone coloring along pairwise disjoint stars and matchings［J］.Discrete Math，2009，309(18): 5596－5609.

［5］Broersma H，Marchal L，Paulusma D，et al.Backbone coloring along stars and matchings in split graphs:their span is close to the chromatic number［J］.Discuss Math Graph Theory，2009，29(1):143－162.

［6］Wang Weifang，Bu Yuehua，Montassier M，et al.On backbone coloring of graphs［J］.J Comb Optim，2012，23(1):79－93.

［7］Bu Yuehua，Zhang Shuiming.Backbone coloring for C5－free planar graphs［J］.J Math Study，2010，43(4):315－321.

［8］卜月华，张水明.没有4－圈的平面图的BB－染色［J］.中国科学:A辑数学，2011，41(2):197－206.

［9］Bu Yuehua，Li Yulin.Backbone coloring of planar graphs without special circles［J］.Theoret Comput Sci，2011，412(46):6464－6468.

(责任编辑 陶立方)

The backbone coloring of planar graphs without 7-cycles

BU Yuehua， BAO Xudong

(College of Mathematics，Physics and Information Engineering，Zhejiang Normal University，Jinhua Zhejiang 321004，China)

The problem of backbone coloring of connected planar graphs without 7－cycles was studied.By using the discharging technique，it was proved that if G is a connected planar graph without 7－cycles and adjacent 4－cycles，then there would have a spanning tree T of G such that(G，T)is BB－4－colorable.The result generalized the sufficient condition for the planar graphs of BB－4－colorable.

planar graph;backbone coloring;spanning tree;cycle

O157.5

A

1001－5051(2015)01－0028－06

�:2014－04－20;

2014－06－12

国家自然科学基金资助项目(11271334)

卜月华(1960－)，男，浙江东阳人，教授，博士.研究方向:组合数学与图论.

10.16218/j.issn.1001－5051.2015.01.005