NIU Jun （牛骏）， SHI Zai-hong （石在虹）， TAN Wen-chang （谭文长）

1. Petroleum Exploration and Production Research Institute of SINOPEC， Beijing 100083， China，E-mail: niujun.syky@sinopec.com

2. State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics and Aerospace Engineering， College of Engineering， Peking University， Beijing 100871， China

Thermal instability and heat transfer of viscoelastic fluids in bounded porous media with constant heat flux boundary*

NIU Jun （牛骏）1， SHI Zai-hong （石在虹）1， TAN Wen-chang （谭文长）2

1. Petroleum Exploration and Production Research Institute of SINOPEC， Beijing 100083， China，E-mail: niujun.syky@sinopec.com

2. State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics and Aerospace Engineering， College of Engineering， Peking University， Beijing 100871， China

2015，27（5）:809-812

A numerical simulation is performed for thermal instability and heat transfer of viscoelastic fluids in bounded porous media under the bottom constant heat flux boundary condition. The results for six different combinations of relaxation and retardation times demonstrate the existence of the thermal instability induced flow bifurcation. It is found that the increase of the relaxation time can enhance the heat transfer efficiency by disturbing the fluid flow and facilitating the bifurcation. The increase of the retardation time can stabilize the flow and postpone the bifurcation， leading to simpler flow pattern and lower heat transfer rate.

thermal instability， heat transfer， viscoelastic fluid， porous media， bifurcation

The thermal instability and the convection heat transfer of fluids in porous media have drawn a great deal of research attention as wide applications are found in many industrial fields such as oil recovery engineering and cooling of power stations［1］. Extensive studies were carried out regarding the thermal convection in Newtonian fluid saturated porous media based on the Darcy’s law［2］， but few studies were related to the thermal convection of the viscoelastic fluid in porous media due to the complicated viscoelastic rheology.

For describing the viscoelastic behavior， the modified Darcy’s law is derived from a macroscopic model， which has thrown light on the study of the viscoelastic fluid flow and the heat transfer in porous media［3］. Kim performed a non-linear stability analysis of the thermal convection in viscoelastic fluid saturated porous media and demonstrated the existence of both the steady and the oscillatory convections， showing that the oscillatory convection always sets in earlier than the steady convection［4］. Fu conducted numerical simulations of the thermal convection of the viscoelastic Oldroyd-B fluid in porous media with isothermal bottom heating， and investigated the flow bifurcation process［5］. The thermal instability of the viscoelastic fluid in open-top porous media under the bottom constant heat flux is also investigated numerically， which shows that the steady and oscillatory convections may coexist， leading to the slightly vibrating Nusselt number approaching a constant［6］. But till now the thermal instability and convection in viscoelastic fluid saturated bounded porous media under constant heat flux boundary condition have not been well studied. This paper studies the heat transfer and thermal instability induced flow pattern transition process of the thermal convection of viscoelastic fluids in bounded porous media heated from below with a constant heat flux.

Our model is a two-dimensional square porous medium of thicknessa . The boundaries are impermeable and adiabatic with the top boundary maintained at a constant temperature T0. The bottom boundary is heated by a constant heat fluxq . The porous medium has a permeabilityK and is saturated with incompressible viscoelastic fluid. The dynamic viscosity， the thermal expansion coefficient， the thermal conductivity， the thermal diffusivity and the density of the fluid are µ，β，k，κandρ， respectively. The modified Darcy’s law is adopted in this paper to de-scribe the flow behavior of the viscoelastic fluid in porous media. With the Oberbeck-Boussinesq approximation， the governing equations for this problem are:

where v∗=（u∗，w∗）is the Darcy velocity，p∗the pressure，g the gravitational acceleration，εand λare the strain retardation time and the stress relaxation time，z is a unit vertical vector， and ρ0the density at temperature T0. The boundary conditions for this model are:

Introducing the stream function and non-dimensionalizing the governing equations by scaling length ofa ， scaling time of a2/κ， scaling temperature of qa/k and scaling velocity of κ/a， we obtain the following equations.

The dimensionless viscoelastic parameters are ε=

For analyzing the heat transfer efficiency in the porous medium， we introduce the bulk-averaged Nusselt number， where the angle bracket represents the long-time average value. As till now no software is available to solve the heat transfer equations for the thermal convection of viscoelastic fluid in porous media due to the coupled and non-linear characteristics， we have developed a numerical simulation program based on the finite difference method. Then the numerical simulation is carried out at variousRatill Ra =250for six different combinations of the viscoelastic parameters: （1）λ=1.0，ε= 0.1， （2）λ=0.3，ε=0.1， （3）λ=0.2，ε=0.1， （4）λ=5.0，ε=0.1， （5）λ=5.0，ε=0.5， （6）λ=5.0，ε=1.0. Cases （1）-（3） have the same value ofεbut differentλ， so the comparison may reveal the influence of the relaxation time on the convection. Similarly，Cases （4）-（6） are used to analyze the influence of the retardation time.

TheN×Nuniform grid is adopted. For ensuring the calculation accuracy and increasing the converging speed， we choose N =128at Ra≤100and N =256at Ra＞100. The increase interval ofRa is first selected as 25 and may become smaller in cases of slow convergence. The input initial data at each Ra are from the results at the previousRa.

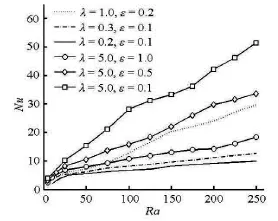
Fig.1 The variation of bulk-averaged Nusselt number as a function of Rayleigh number in Cases （1）-（6）

During the calculation， it is found that the time history of the transient Nusselt number may assume two different modes. One is a steady mode with the Nusselt number approaching a constant value， this mode corresponds to the steady convection as is widely found in the thermal instability induced convection of Newtonian fluids. The other is an oscillatory mode with the transient Nusselt number vibrating quasi-periodically， which is caused by the oscillatory convection［6］. This means that there exist both steady and oscillatory convections in the thermal convection of viscoelastic fluids in porous media under the bottom constant heat flux. For the oscillatory mode， we calculate the average value of the transient Nusselt numbers within several vibrating periods as the bulk-averaged Nu .

Figure 1 exhibits the curves of the bulk-averaged Nu as a function ofRa corresponding to Cases （1）-（6）. It can be seen that the averaged Nusselt number always increases with the increase of the Rayleigh number. The comparison of curves in Cases （1）-（3）shows that at each fixed Rathe case with a larger value ofλcorresponds to a largerNu， which implies that the increase of the relaxation time might disturb the flow and increase the heat transfer rate in the viscoelastic fluid saturated porous media. The curves in Cases （4）-（6） show that for a fixed Rayleigh number，Nudecreases with the increase ofε. So we conclude that the increase of the retardation time can stabilize the flow in the porous medium and reduce the heat transfer efficiency at the same time.

It is noted that theNuvs.Racurves appear like polylines， each consisting of several quasi-linear parts with different gradients. For instance， in Case （6），the typical quasi-linear parts are from Ra =25to Ra =75and from Ra =100to Ra=125. Based on the previous studies［5］， this implies the existence of the flow bifurcations appearing intermittently with the increase of the Rayleigh number. And the end point of one quasi-linear part， which may also be the starting point of the next one， is the flow bifurcating point.

Fig.2 Snapshots of stream function contours at Ra=50， 150 and 250 in Cases （1）-（3）

For demonstrating the existence of the thermal instability induced flow bifurcation and analyzing the flow pattern transition processes， the snapshots of the stream function contours， which are equivalent to the streamlines， are plotted for Cases （1）-（6） at different Rayleigh numbers.

Figures 2（a）-2（c） show the stream function contours in Case （1） at Ra=50， 150 and 250， respectively. The flow pattern atRa=50appears in an unsteady two-cell roll mode， with the size and the location of each cell changing periodically. This reveals the domination of the oscillatory convection at this point，and the steady convection is suppressed. AtRa =150， the flow pattern turns into the mode of a two-cell roll alternating with a three-cell roll. In a typical period， a third cell first arises at the top boundary and enlarges to the size of the other two cells forming a three-cell roll mode， later it starts to shrink and finally disappears， with the flow pattern turning back to the two-cell roll mode. WhenRa increases to 250， the flow pattern is in an unsteady three-cell roll mode. The transition of the flow pattern in Case （1） clearly shows the effect of the flow bifurcation， which also influences the flow pattern evolutions in Cases （2） and （3）.

Figures 2（d）-2（f） and 2（g）-2（i） show the snapshots of the stream function contours in Cases （2） and （3）at Ra =50， 150 and 250. At Ra=50the flow patterns in both Cases （2） and （3） are in the steady one cell roll mode. It reveals that the steady convection suppresses the oscillatory convection at this point. But whenRareaches 150， in both cases， the oscillatory convection dominates and the flow patterns begin to show a vibrating nature， in Case （2） an unsteady twocell roll and in Case （3） a one-cell roll alternating with two-cell roll. In Case （3）， an unsteady two-cell roll mode becomes evident at Ra=250while in Case （2），the same feature shows as that atRa=150. Comparing the stream function contours in Cases （1）-（3） at each three Ra， it is noted that the flow pattern turns more and more complicated with the increase ofλ.

Fig.3 The time history of transient Nusselt number at Ra=150 in Cases （1）-（3）

The time histories of the Nusselt number at Ra= 150 in Cases （1）-（3） are plotted in Fig.3. The quasiperiodic vibration is clearly seen in all three cases，which reveals the domination of the oscillatory convection. Figure 3 also shows that the case with a larger value of λhas a smaller vibration period， which corresponds to a slower cell roll oscillation of the unsteady flow patterns plotted in Fig.2. Combining the discussion for Figs.2 and 3， we conclude that the increase of the relaxation time helps to disturb the flow，resulting in earlier flow bifurcation and faster flow pattern oscillation. The more complex flow pattern together with its faster vibration leads to more severe the-rmal convection and increases the heat transfer rate as shown in Fig.1.

Fig.4 Snaphots of stream function contours at Ra=50， 150 and 250 in Cases （4）-（6）

The snapshots of the stream function contours in Cases （4）-（6） at Ra=50， 150 and 250 are plotted in Figs.4（a）-4（c）， 4（d）-4（f） and 4（g）-4（i）. The flow bifurcations are also found in these three cases. Especially in Case （4） with the largest value ofλ/ε， the flow pattern shows a severe transition in an unsteady twocell roll mode atRa=50， a four-cell roll alternating with five-cell roll mode atRa=150and an unsteady six-cell roll mode atRa=250. Comparing the flow patterns in Cases （4）-（6） at each Rayleigh number， it is found that the flow pattern gets more and more complicated with the decrease ofε.

Fig.5 The time history of transient Nusselt number at Ra= 150 in Cases （4）-（6）

Figure 5 shows the time histories of the Nusselt number in Cases （4）-（6）. Clearly， all three curves see a quasi-periodic vibration and the period increases with the increase ofε. So we conclude that the increase of the retardation time helps stabilize the thermal instability induced convection and postpone the flow bifurcation. The corresponding simpler flow pattern and its slower oscillatory period lead to a lower heat transfer rate.

In summary， the thermal instability induced convection and heat transfer of the viscoelastic fluid in bounded porous media under the bottom constant heat flux boundary condition is studied in this work. A program based on the finite difference method is developed for simulating the flow and the heat transfer process， and six different combinations of the relaxation time and the retardation time are selected for the calculation and analysis. The results show that the heat transfer rate of the thermal convection in the porous media increases with the increase of the Rayleigh number. The increase of the relaxation time helps to disturb the flow and facilitate earlier flow bifurcation，the resultant more complicated flow pattern together with the severe oscillation mode enhances the heat transfer rate of the viscoelastic fluid in porous media. On the other hand， the increase of the retardation time tends to stabilize the convection and postpone the flow bifurcation， leading to simpler flow pattern and slower mode oscillation， which suppresses the heat transfer in the porous media.

As temperature has little influence on the fluid flow and heat transfer in porous media， and due to the lack of appropriate temperature measuring techniques，no experimental result regarding the thermal convection of the viscoelastic fluid in porous media is reported till now. It may be beneficial to find an appropriate experimental way to measure the heat transfer rate and demonstrate the flow bifurcation.

References

［1］ NIELD D. A.， BEJAN A. Convection in porous media［M］. 4th Edition， New York， USA: Springer-Verlag， 2013.

［2］ BERA P.， PIPPAL S. and SHARMA A. K. A thermal non-equilibrium approach on double-diffusive natural convection in a square porous-medium cavity［J］. International Journal of Heat and Mass Transfer， 2014，78: 1080-1094.

［3］ ALISHAEV M. G.， MIRZADJANZADE A. K. For the calculation of delay phenomenon in filtration theory［J］. Izvestya Vuzov Neft i Gaz， 1975， 6: 71-75.

［4］ KIM M. C.， LEE S. B. and KIM S. et al. Thermal instability of viscoelastic fluids in porous media［J］. International Journal of Heat and Mass Transfer， 2003， 46: 5065-5072.

［5］ FU C.， ZHANG Z. and TAN W. Numerical simulation of thermal convection of an Oldroyd-B fluid in a porous square box heated from below［J］. Physics of Fluids，2007， 19: 104107.

［6］ NIU Jun， SHI Zai-hong and TAN Wen-chang. The viscoelastic effects on thermal convection of an Oldroyd-B fluid in open-top porous media［J］. Journal of Hydrodynamics， 2013， 25（4）: 639-642.

10.1016/S1001-6058（15）60542-X

（September 11， 2015， Revised September 18， 2015）

* Project supported by the National Key Basic Research Development Program of China （973 Program， Grant Nos. 2006CB705803， 2013CB531200）， the National Natural Science Foundation of China （Grant No. 21571188）.

Biography: NIU Jun （1985-）， Male， Ph. D.， Senior Engineer