Ufuk OZTURKSuleyman CENGIZ Esra Betul KOC OZTURK

Department of Mathematics，Faculty of Science，C¸ankırı Karatekin University，C¸ankırı 18100，Turkey

MOTIONS OF CURVES IN THE GALILEAN SPACE G3∗

Ufuk OZTURK†Suleyman CENGIZ Esra Betul KOC OZTURK

Department of Mathematics，Faculty of Science，C¸ankırı Karatekin University，C¸ankırı 18100，Turkey

E-mail：ozturkufuk06@gmail.com；suleymancengiz@karatekin.edu.tr；e.betul.e@gmail.com

In this article，we study the flows of curves in the Galilean 3-space and its equiform geometry without any constraints.We find that the Frenet equations and the intrinsic quantities of the inelastic flows of curves are independent of time.We show that the motion of curves in the Galilean 3-space and its equiform geometry are described by the inviscid and viscous Burgers'equations.

Galilean geometry；equiform geometry；motions of curves；inextensible flows；Burgers'equation；Frenet frames

2010 MR Subject Classification 53A35；53C44

1 Introduction

Many nonlinear events of the natural and applied sciences were modeled by use of the motions of space curves such as dynamics of vortex filaments，motions of interfaces，shape control of robot arms，propagation of flame fronts，image processing，supercoiled DNAs，magnetic fluxes，deformation of membranes and dynamics of proteins.These nonlinear applications need to describe the evolution of the curves in terms of the differential equations characterizing the motion of curves as a family.Integrability of these motions satisfies the conservation of many global invariants.

The subject of how a family of curves evolve in time was of great interest and was widely investigated by many authors.In 1992 Nakayama and others explained that the close relation between the integrable evolution equations and the motion of curves is based on the equivalence of Serret-Frenet equations and the inverse scattering problem at zero eigenvalue［1］.So they identified the evolution equations that govern the 2-D and 3-D motions of the curves.Later they investigated the motions of the plane curves that the curvature obeys the mKDV equation and its hierarchy［2］.Generalization of the motion of curves to n-dimensional Euclidean space is worked in［3］.Many well-known integrable equations or their hierarchies related to the motions of curves in space can be found in many subsequent works［4-12］.

In the Galilean space which is a real Cayley-Klein space with projective signature，the subject of curve flows needs further investigation.Inextensible flows of curves in Galileanand pseudo-Galilean space are studied at［13，14］.In［15］，Yoon examined inextensible flows of curves in the equiform geometry of Galilean 3-space.Intrinsic equations for a generalized relaxed elastic line on an oriented surface in the Galilean space are derived in［16］.

In this article we study the flows of curves in the Galilean 3-space and in its equiform geometry without any constraints.In Section 2 we summarize the preliminaries of the Galilean 3-space.In Section 3 we investigate the evolution of a one parameter family of smooth curves in the Galilean 3-space with use of Serret-Frenet equations.We derive the equations for the evolutions of curvature κ and torsion τ which induce the inviscid Burgers'equation.Then some particular cases are considered.In the final section，the curve evolution in the equiform geometry of the Galilean 3-space is studied and the equations for the evolutions of the equiform curvature ˜κ and the equiform torsion˜τ which induce the viscous Burgers'equation are expressed.Also we show that the flows of the inextensible curves in the Galilean 3-space and in the equiform geometry of G3are independent of time.

2 Galilean Space G3

The Galilean space G3is one of the real Cayley-Klein spaces.It has projective signature（0，0，+，+）as in［17］.The absolute figure of the Galilean space G3consists of an ordered triple｛w，f，I｝where w is the ideal（absolute）plane，f is the line（absolute line）in w and I is the fixed elliptic involution of points of f.

In the non-homogeneous affine coordinates the similarity group H8of the Galilean space G3has the following form

where aijand ϕ are real numbers.

In what follows the coefficients a12and a23will play the special role.In particular，for a12=a23=1 group（2.1）becomes the group B6⊂H8of isometries of the Galilean space G3as follows

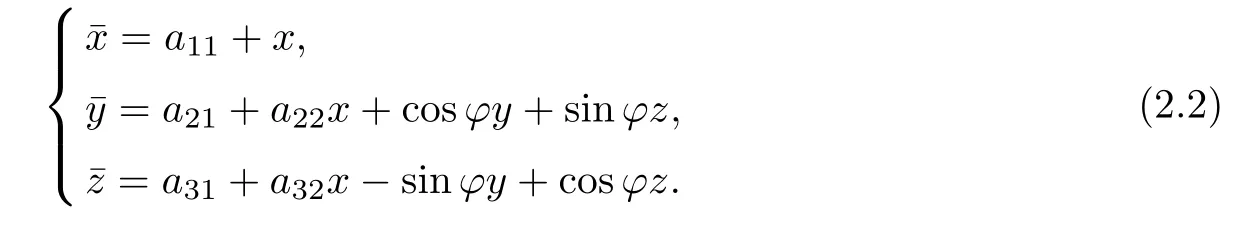
The Galilean scalar product of two vectors u=（u1，u2，u3）and v=（v1，v2，v3）can be written as

It leaves invariant the Galilean norm of the vector u=（u1，u2，u3）defined by

Let α be a curve in the Galilean space G3defined by the arc length

where x（s），y（s），z（s）∈C3.

The curve α in the Galilean space G3is defined by the arc length parameter s with differential form ds=dx as

The curvature κ（x）and the torsion τ（x）of the curve α are defined by

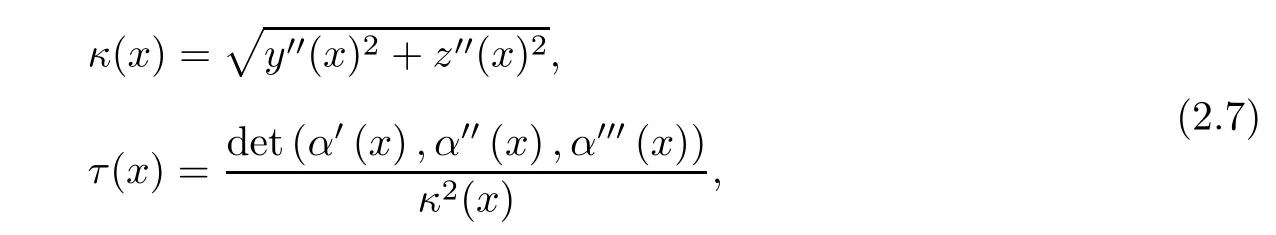
respectively.The Frenet frame of the curve α is given by

where t，n and b are called the tangent vector，principal normal vector and binormal vector fields of the curve α，respectively.Then the Frenet equations of the curve α can be found as

where t，n and b are mutually orthogonal vectors［17-21］.

3 Motions of Curves in the Galilean Space G3

In this section we study the curve evolution in the Galilean space G3by using the Frenet frame structure to obtain some related integrable equations.

Let us consider a one parameter family of smooth admissible curves r（u，t）in the Galilean space G3where t denotes the time or the scale and u parametrizes each curve of the family. We assume that this family r（u，t）evolves according to the evolution equation

and

where a，b，c are arbitrary functions.

Let

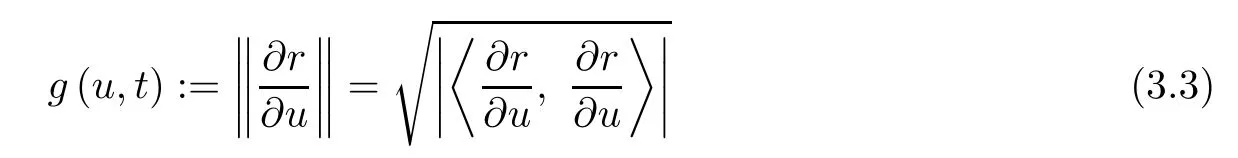
denote the length along the curve.The arc length parameter s is given by

Then from（2.9）we have

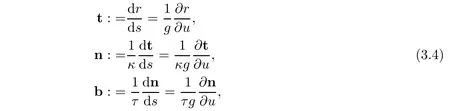
and

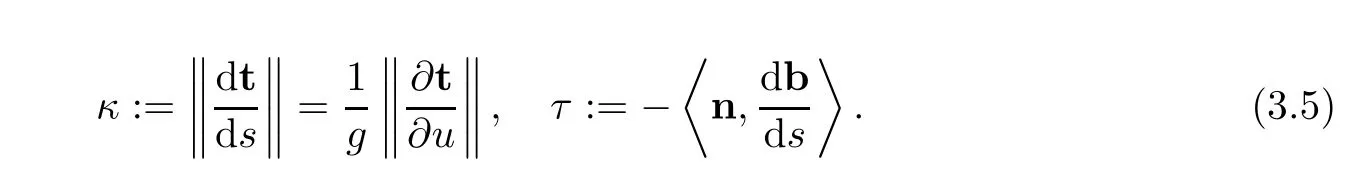
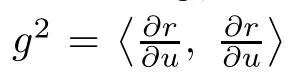
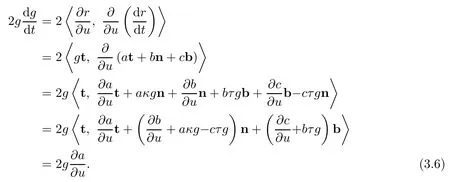
So we get the equation

It is important to notice that u and t are independent but s and t are not independent.As a consequence，we have

We can evaluate the evolution equation of the unit tangent vector t as

Similarly for the evolution of the unit normal vector n we have

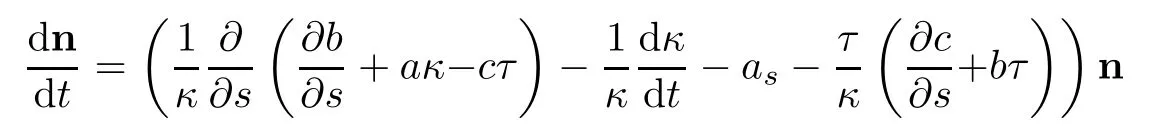
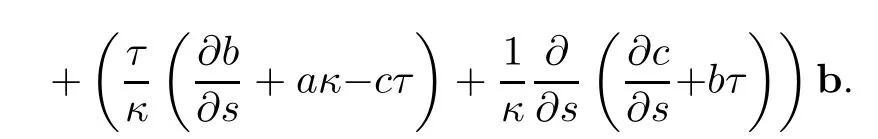
and

Also the evolution of the binormal vector b becomes

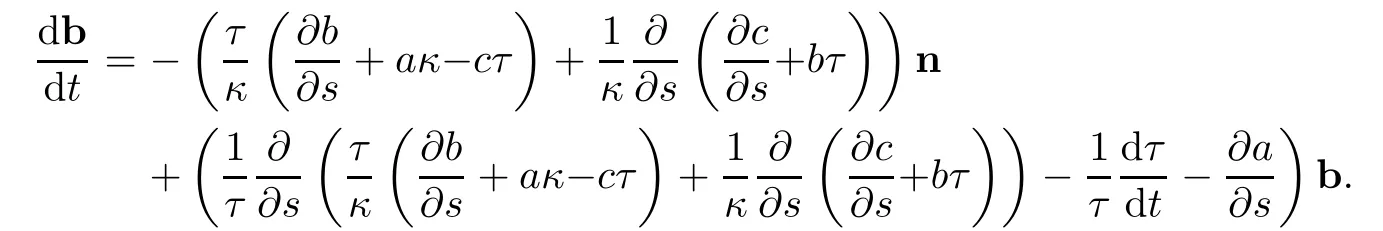
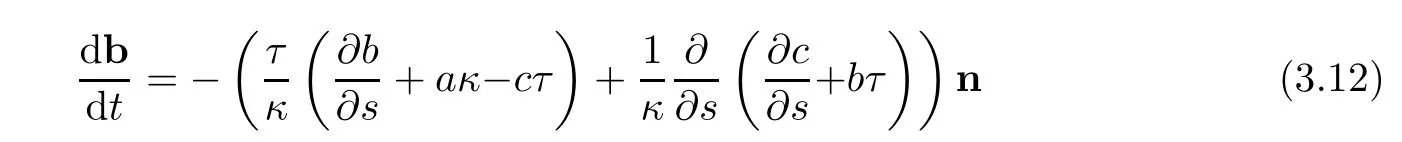
and

Since=0 and=0 for all（u，t）we get

and

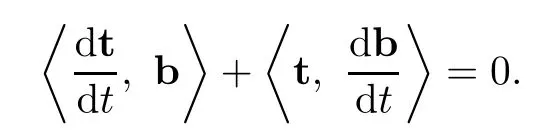
Then by equations（3.9），（3.10）and（3.12）we can write

and

Hence the evolution equations of the Frenet frame take the form

and for the intrinsic quantities the evolution equations become

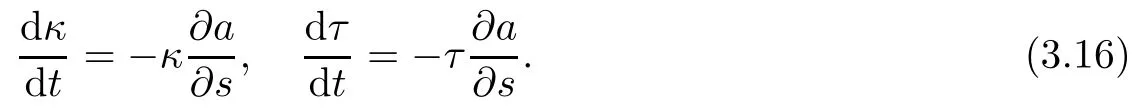
Case 1 Burgers'equations describe various kinds of phenomena such as a mathematical model of turbulence and the approximate theory of flow through a shock wave traveling in viscous fluid.The inviscid Burgers'equation is a model for the nonlinear wave propagation，especially in fluid mechanics.It takes the form

where ψ（s，t）is a solution of the equation.Choosing a=κ or a=τ in equations（3.16）we see that the intrinsic quantities κ and τ evolve according to the inviscid Burgers'equation.

Definition 3.1 A curve evolution r（u，t）and its flowin the Galilean space G3are said to be inextensible if

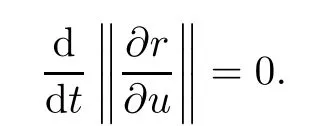
If the family of curves r（u，t），which is given by（3.1），is inextensible，then from（3.7）for all（u，t）we get

and

Therefore we can give the following corollary.

Corollary 3.2 The family of curves r（u，t），which is given by（3.1），is inextensible if and only if for all（u，t）

If we now restrict ourselves to arc length parameterized curves that undergo purely inextensible deformations，that is g（u，t）=ξ（u）=1 and，then the local coordinate u corresponds to the arc length parameter s.Thus the flow of the curve is expressed as

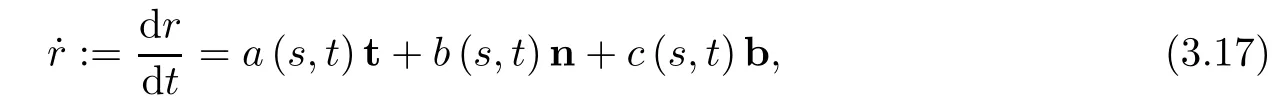
and the evolution equations of the Frenet frames with the intrinsic quantities can be given by

Proposition 3.3 If the family of curves r（u，t），which is given by（3.1），is inextensible then the Frenet vectors，the curvature and the torsion are not time dependent.

4 Motions of Curves in the Equiform Geometry of G3

Let α:I→ G3be a curve with the arc length parameter s.If we write this curve in another parametric representation α（σ）such that

Here we can write

Also the equiformly invariant Frenet vectors T，N and B are related to the Galilean Frenet vectors t，n and b as

We assume that the equiformly invariant arc length parameter of the family r（u，t）is defined as a function of u by

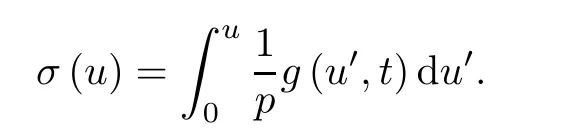
The motion the family r（u，t）can be expressed in the form

where W，U and V are arbitrary functions.The preceding motion of the family r（u，t）is related with motion（3.1）in the Galilean space G3as

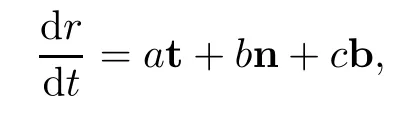
where a=pW，b=pU and c=pV.Using the formulas in Section 3，we obtain

or

Using equations（4.4）and（3.15）the evolution of the equiformly invariant tangent vector field T is calculated as

Similarly，we can write the evolutions of the equiformly invariant principal normal and binormal vector fields，the equiform curvature˜κ and the equiform torsion˜τ respectively as follows:

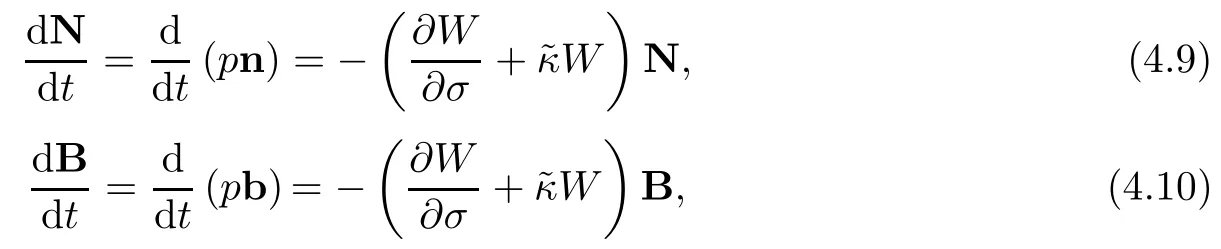
Case 2 Viscous Burger's equation can be thought of as a one dimensional analog of the Navier-Stokes equations which model the behavior of viscous fluids.As such，it is a useful model equation on which to investigate techniques that might be applied to complicated fluid flow problems.It is given by the equation

where ψ（s，t）is a solution of the equation.Choosingin equation（4.11）we see that the intrinsic quantity˜κ evolves according to the viscous Burgers'equation.

If the family of curves r（u，t），which is given by（4.5），is inextensible，then for all（σ，t）we have

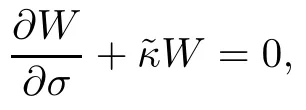
and from（4.2）we get

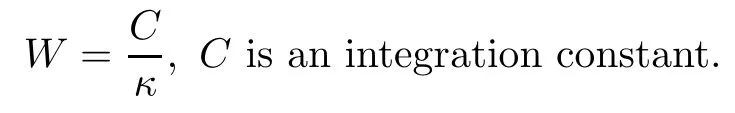
Therefore we can give the following corollary.

Corollary 4.1 The family of curves r（u，t），which is given by（4.5），is inextensible if and only if for all（u，t）the coefficient W of the tangent vector T is equal to

where C is an integration constant.

From（4.8）-（4.10）and Corollary 4.1 we have the following proposition.

Proposition 4.2 If the family of curves r（u，t），which is given by（4.5），is inextensible，then the Frenet vectors，the curvature and torsion are not time dependent.

［1］Kazuaki N，Harvey S，Miki W.Integrability and the motion of curves.Phys Rev Lett，1992，69（18）: 2603-2606

［2］Kazuaki N，Miki W.Motion of curves in the plane.J Phys Soc Japan，1993，62（2）:473-479

［3］Joel L，Ron P.Curve motion inducing modified Korteweg-de Vries systems.Phys Lett A，1998，239（1-2）: 36-40

［4］Chou K S，Qu C Z.The KdV equation and motion of plane curves.J Phys Soc Japan，2001，70（7）: 1912-1916

［5］Chou K S，Qu C Z.Integrable motions of space curves in affine geometry.Chaos Solitons Fractals，2002，14（1）:29-44

［6］Chou K S，Qu C Z.Integrable equations arising from motions of plane curves.Phys D，2002，162（1-2）: 9-33

［7］Chou K S，Qu C Z.Motions of curves in similarity geometries and Burgers-mKdV hierarchies.Chaos Solitons Fractals，2004，19（1）:47-53

［8］Raymond E G，Dean M P.The Korteweg-de Vries hierarchy as dynamics of closed curves in the plane. Phys Rev Lett，1991，67（23）:3203-3206

［9］Chou K S，Qu C Z.Integrable equations arising from motions of plane curves II.J Nonlinear Sci，2003，13（5）:487-517

［10］Metin G.Motion of curves on two-dimensional surfaces and soliton equations.Phys Lett A，1998，241（6）: 329-334

［11］Kazuaki N.Motion of curves in hyperboloids in the Minkowski space II.J Phy Soc Japan，1999，68（10）: 3214-3218

［12］Schief W K，Rogers C.Binormal motion of curves of constant curvature and torsion.Generation of soliton surfaces.R Soc Lond Proc Ser A Math Phys Eng Sci，1999，455（1988）:3163-3188

［13］Alper O¨O，Mustafa Y.Inextensible curves in the Galilean space.Int J Phy Sci，2010，5（9）:1424-1427

［14］Alper O ¨O，Mustafa Y，Mihriban K.Inelastic admissible curves in the Pseudo-Galilean space G13.Int J Open Probl Comput Sci Math，2011，4（3）:199-207

［15］Dae W Y.Inelastic flows of curves according to equiform in Galilean space.J Chungcheong Math Soc，2011，24（4）:665-673

［16］Tevfik S¸.Intrinsic equations for a generalized relaxed elastic line on an oriented surface in the Galilean space.Acta Math Sci，2013，33B（3）:701-711

［17］Blaˇzenka D，ˇZeljka M ˇS.Special curves on ruled surfaces in Galilean and Pseudo-Galilean spaces.Acta Math Hungar，2003，98（3）:203-215

［18］Boris J P，Ivan K.The equiform differential geometry of curves in the Galilean space G3.Glas Mat Ser III，1987，22（2）:449-457

［19］Boris J P.The general solution of the Frenet system of differential equations for curves in the Galilean space G3.Rad Jugoslav Akad Znan Umjet，1990，（450）:123-128

［20］Otto R.Die Geometrie des Galileischen Raumes.Graz:Forschungszentrum Graz Mathematisch-Statistische Sektion，1985

［21］Isaak M Y.A Simple Non-Euclidean Geometry and its Physical Basis.New York:Springer-Verlag，1979

∗Received March 17，2014；revised April 24，2015.

†Corresponding author:Ufuk OZTURK