Ying WANG（王影）

School of Mathematics and Information Science，North China University of Water Resources and Electric Power，Zhengzhou 450011，China

Mingxin WANG（王明新）

Natural Science Research Center，Harbin Institute of Technology，Harbin 150080，China

SOLUTIONS TO NONLINEAR ELLIPTIC EQUATIONS WITH A GRADIENT∗

Ying WANG（王影）

School of Mathematics and Information Science，North China University of Water Resources and Electric Power，Zhengzhou 450011，China

E-mail：feelyeey@163.com

Mingxin WANG（王明新）

Natural Science Research Center，Harbin Institute of Technology，Harbin 150080，China

E-mail：mxwang@hit.edu.cn

In this article，we consider existence and nonexistence of solutions to problem

quasilinear elliptic equations；existence and nonexistence；gradient terms；singular weights

2010 MR Subject Classification 35D05；35D10；35J92；46E30

1 Introduction

In this work，we study existence and nonexistence of solutions to the problem

where 1＜p＜+∞，Ω⊂RNis a smooth bounded domain，and the operator∆pstands for the p-Laplacian defined by∆pu=div（|∇u|p-2∇u）.Throughout this paper，we assume that for any compact subset ω⊂Ω，there exists a positive constant fωsuch that

For the problem

where 1≤q≤p，g（x，u）∈L1（R），and the data f in suitable Lebesgue spaces，has been exhaustively studied.We refer the readers to［1-4］and the references therein for semilinear elliptic problem，and to［5-15］and the references therein for quasilinear elliptic problem.If g（x，u）=1/|u|αwith α＞0 is singular at u=0，the existence of solutions to（1.1）with p=2 has been obtained in［16-18］for 0＜α≤1，and the authors in［19］have proved that α＜2 is necessary and sufficient for the existence of solutions in H10（Ω）for every f with sufficient regularity and satisfying（1.2）.

In this article，we extend the results of［19］to general case p＞1.That is，we consider that g（x，u）is singular at u=0 for a.e.x∈Ω，and obtain existence and nonexistence of solutions to problem（1.1）.Here is our main result.

Theorem 1.1 Suppose p＞1，f∈L1（Ω）such that（1.2）holds.Let h:（0，+∞）→［0，+∞）be a continuous nonnegative function which is nonincreasing in a neighborhood of 0，and assume that

If

then problem（1.1）admits a positive solution in）for any max

Furthermore，if there exist constants s0＞0 and g0＞0 such that

then the solution belongs to W1，p（Ω）.

2 Preliminaries

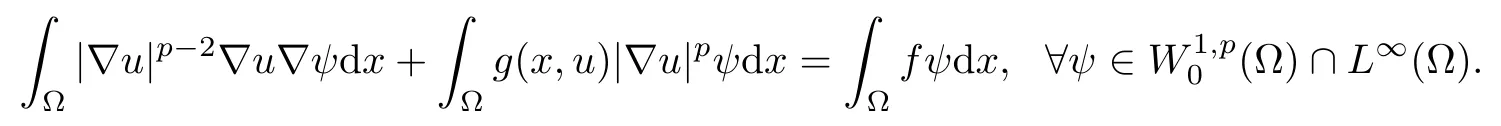
To obtain the existence of solutions to problem（1.1），we need to study the behavior of g（x，u）at the neighborhood of u=0.The following result shows that the solution u is bounded below away from 0 in every compact subset of Ω，and hence，we conclude that g（x，u）is bounded in every compact subset contained in Ω，if u is bounded.

Proposition 2.1 Suppose that f∈Lr（Ω）with r＞N/p，satisfies（1.2）and that h is such that（1.3）holds.Let ω be an open subset compactly contained in Ω，then there exists a constant cω＞0 such that every solution（supersolution）in Ω，of the equation

satisfies

Proof From assumption（1.3）it follows that the function h may be integrable near 0，set，thenis non-integrable near 0.For any s＞0，we define the nonincreasing function

Then，

Because z∈C（¯Ω）and z＞0 in Ω，then z is bounded away from 0 in any compact subsetand takeas a test function in（2.1），from ˜h（s）≥h（s），we deduce that

Let v=ψ（z），we have

This implies that v is a subsolution of the equation

We claim that

（ii）b（s）satisfies the Keller-Osserman condition，i.e.，

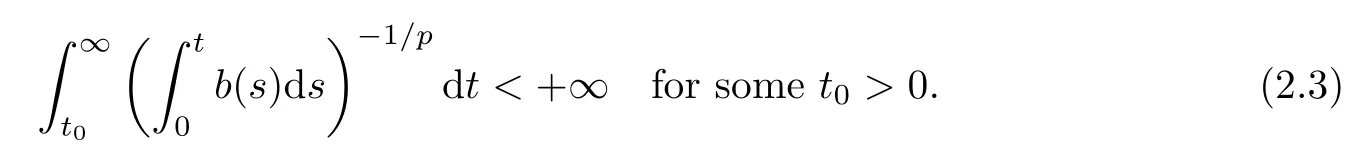
Indeed，let ψ（z）=s，then

Because h（s）is nonincreasing in a neighborhood of 0，there exists z0∈（0，1）such that˜h is decreasing in（0，z0］.Let z≤z0，then

To prove（2.3），it is sufficient to prove

Using the change ψ（z）=s again，we obtain

From the define of˜h，it follows from（1.3）that

Let t0＞0 be such that，then to prove（2.3），it is sufficient to prove that

Therefore，it follows from［20］that for any compact subset ω⊂Ω，there exists a constant Cωsuch that

Moreover，since ψ is nonincreasing，we have

3 Existence

In this section，we study the existence of positive solution for problem（1.1）if f is sufficiently regular，and give the proof of Theorem 1.1.

3.1 Solutions of Problem with Regular Function

To prove Theorem 1.1，we give the following existence result for，first.

Proof As in［19］，we define a suitable sequence of Carath´eodory functions gnby

where Tn（f）is the k-truncation of f defined by

which implies that un＞0 in Ω（see［22］）.Moreover，From（1.4）and from the definition of gn，we have that，for any n∈N，

It follows from the regularity results in［23，24］that un∈Cα（Ω）for some α∈（0，1）.

For any n≥n0，we have that gn（x，s）≤g（x，s）≤h（s）for a.e.x∈Ω and every s＞0，thenis a supersolution of

We deduce from Proposition 2.1 that for any compact subset ω⊂Ω，there exists a positive constant cωsuch that

Let ε→0，we obtainThen，take un∈W1，p0（Ω）∩L∞（Ω）as a test function in（3.1），we have

where S is the Sobolev constant.Therefore，there exist constants C1and C2independent of n，such that

and hence，up to subsequences，un⇀u weakly inBy the weak-∗convergence in L∞，we have thatFix k＞0，similar to the proof in［19］，we have that Tk（un）→Tk（u）strongly in

Now，we prove that un→u strongly inLetL∞（Ω）be a test function in（3.1），then

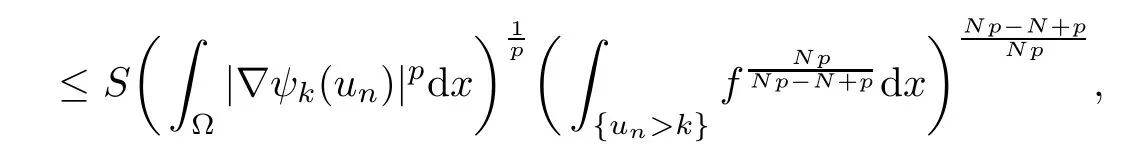
which implies that

Let E⊂Ω be a compact subset，then

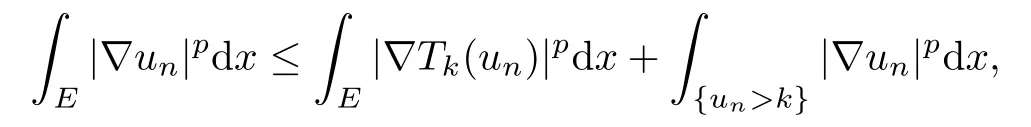
3.2 Proof of Theorem 1.1

To prove that u is a weak solution of（1.1），it is sufficient to prove that

Let n→+∞in（3.3），we have

If E⊂Ω is a compact subset，then

and

we have

It follows from f∈L1（Ω）that

Moreover，since Tk（un）→ Tk（u）strongly in，we see from （3.6）that gn（x，is equiintegrable，and equality（3.5）holds by applying the Vitali'theorem.Moreover，

As Tn（f）→f strongly in L1（Ω），we have that

Letting n→+∞in second inequality in（3.4），we obtain that g（x，u）|∇u|pu∈L1（Ω），which implies that the solution u itself is allowed as a test function in（1.1）.

Proof Let fn∈L∞be such that fn↗f in L1（Ω），then by Theorem 3.1，there exists a sequence of positive solutionsto problems

for all n∈N.Then unis a supersolution of（2.1）with f=fn，applying Proposition 2.1，it follows that，for any compact subset ω in Ω，there exists a positive constant c′ωsuch that

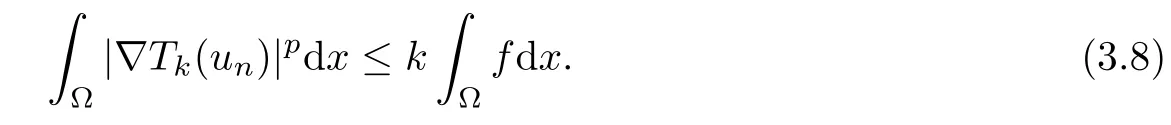
Therefore，up to sequences，Tk（un）⇀Tk（u）weakly in.We claim that Tk（un）→Tk（u） strongly in

Indeed，let ω⊂Ω be a compact subsetsuch that suppφ⊂ω，and as in［12］and［13］，let ϕk（un）=T2k（un-Tj（un）+Tk（un）-Tk（u））with j＞k，then∇ϕk（un）≡0 if un＞2k+j，and

Moreover，ϕk（un）≤0 if and only if un≤Tk（u）≤k.Then，takeas a test function in（3.7），we have that

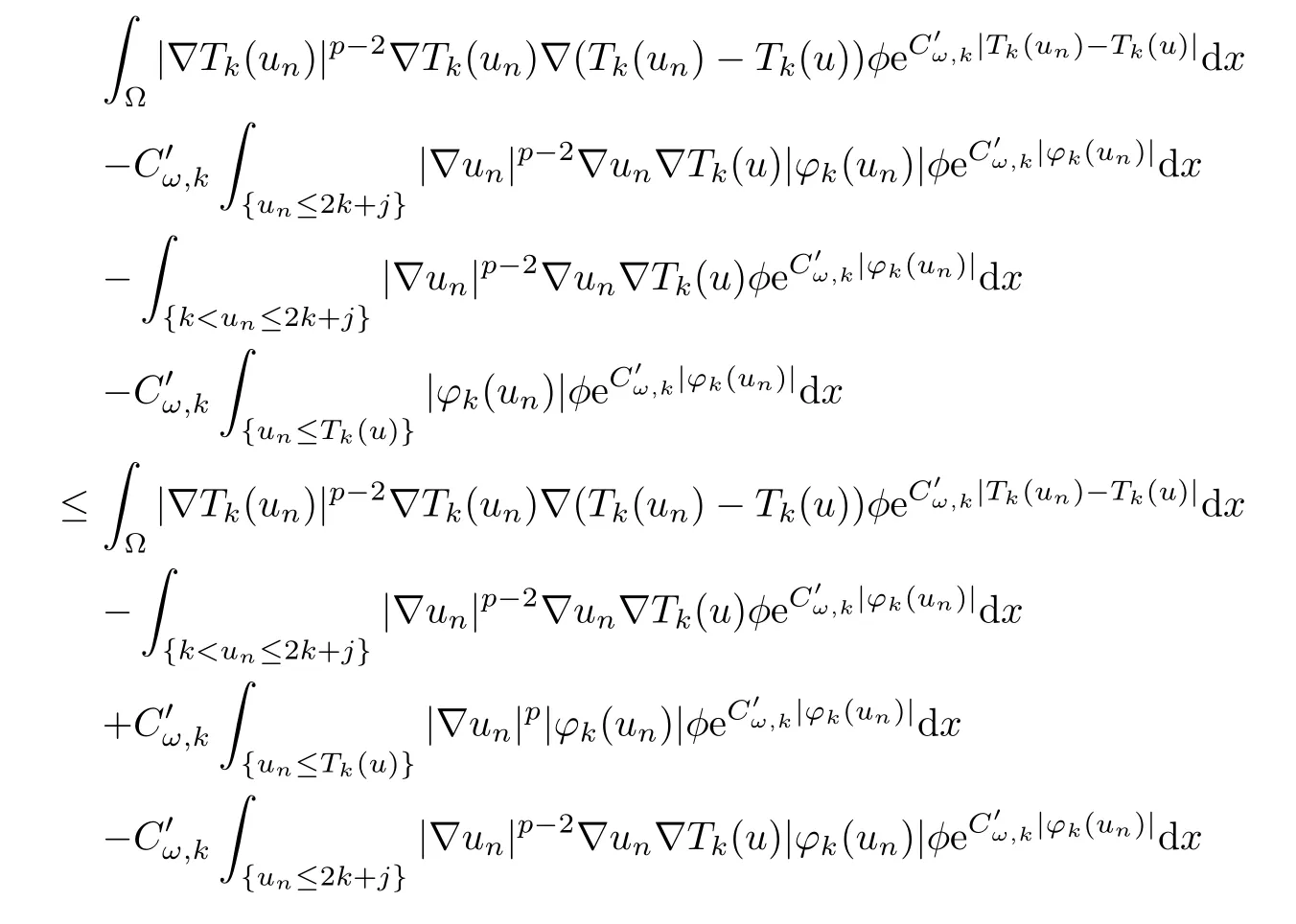
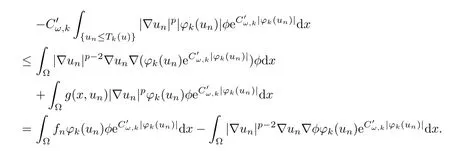
That is，

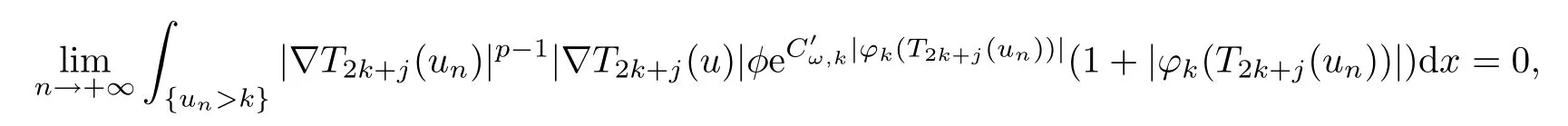
and we deduce from Tk（un）⇀Tk（u）weakly inand Tk（un）→Tk（u）almost everywhere，that

Applying Lemma 4.2 in［25］，it deduces from（3.8）thatwhere Mtdenote the space of measurable function v:Ω→R such that there exists a constant c＞0，and

where|Ω|denotes the Lebesgue measure of Ω.Then，equipped with the pseudo-norm

the space Mt（Ω）is a Banach space.Since Ω is bounded，for every ε∈（0，p-1］，there exists a positive constant C such that

Then，let n，j→+∞in（3.10），we have that

By the fact that

which implies that Tk（un）→Tk（u）strongly inand completes this claim.

To conclude the proof of Theorem 1.1，it is sufficient to prove that

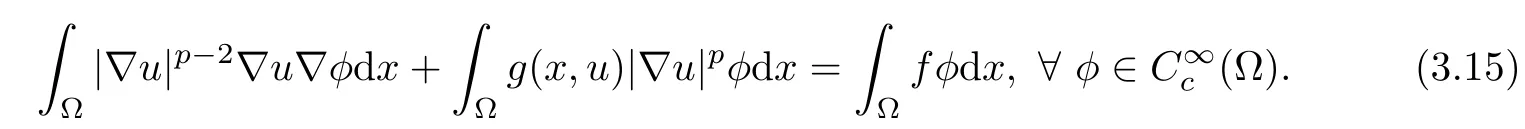
Let E⊂ω be a compact subset in Ω，then

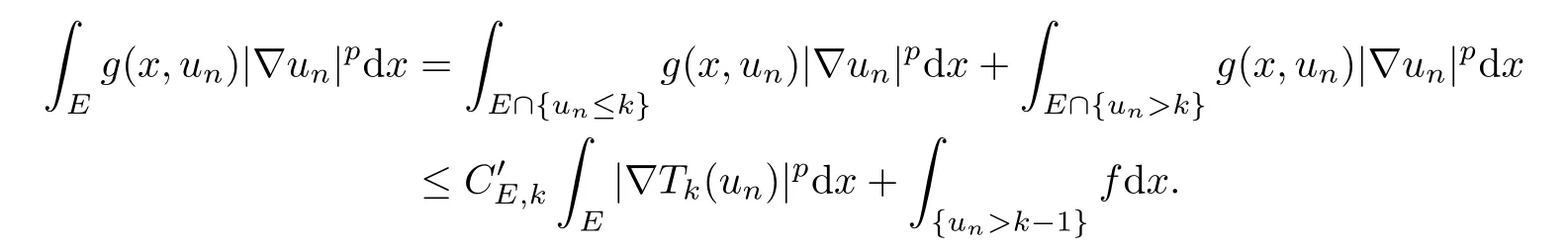
Because Tk（un）→Tk（u）strongly inand f∈L1（Ω），we have thatis local equiintegrable.

Combing with g（x，un）∇un→ g（x，u）∇u a.e.in Ω（see［26］），it follows from the Vitali' theorem that

As un→u strongly in W1，σ（Ω）for any max｛p-1，1｝≤σ＜µ，we conclude（3.15）by letting n→+∞in the following equality，

If（1.5）holds，let k≥max｛s0，1｝，then it follows from（3.16）that

combing with（3.8），we havewhich means that unis bounded in W1，p（Ω）.Similar to the proof of Theorem 3.1，we have that there exists a solution u∈W1，p（Ω），which is the limit（a subsequence of）of un. □

3.3 Other Existence Results

If f∈Lr（Ω）with r＞Np，then，combining with the methods in［27］，we have the following results.

Theorem 3.2 Suppose f∈Lr（Ω）with r＞Np，such that（1.2）holds，then under the conditions of Theorem 1.1，problem（1.1）has a positive solution in

If g（x，s）=1/sα，consider the problem

where α＞0.We have the following result by applying Theorem 3.2.

Corollary 3.3 Suppose f∈Lr（Ω）with r＞Np，such that（1.2）holds.If α＜p，then problem（3.17）has a positive solution in W1，p0（Ω）.

Proof Obviously，if α＜p，then h（s）=g（x，s）=|s|-αsatisfies（1.3）.Since f∈Lr（Ω），r＞Np，it follows from Theorem 3.2 that there exists a positive solution u∈W1，p（Ω）∩L∞（Ω）.□

4 Nonexistence

In this section，we consider the nonexistence of positive solution for problem（1.1）if assumption（1.3）does not hold，and obtain the following nonexistence result.

For any f∈Lr（Ω）with r＞N/p，we consider the following eigenvalue problem

then，we see from［28］that the first eigenvalue，denote λ1（f），is positive，simple and isolated，and the associated eigenfunction is of definite sign in Ω.

Theorem 4.1 Let f∈Lr（Ω）with r＞N/p，be such that（1.2）holds，and assume that there exists a nonnegative continuous function h:（0，+∞）→［0，+∞），such that

and

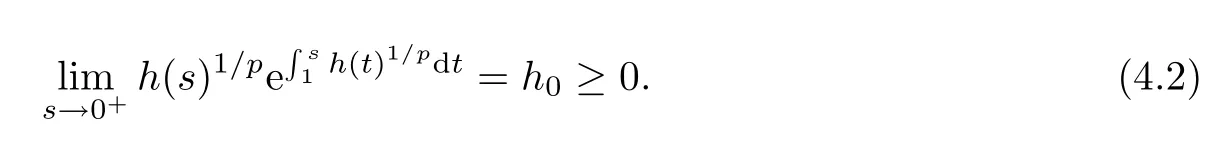
If

then problem（1.1）does not have any positive solution in）for λ1（f）＞1.

Proof Assume by contradiction that there exists a solution u∈）to problem（1.1）.Since g≥0，we can assume that h（s）≡0 if s≥1，and we define the following two nonnegative function G，σ∈C1（［0，+∞）as

Since p＞1，it deduces from（4.1）and（4.2）that G（0）=0，σ（0）=0 and

Now，we construct a nonnegative continuously differentiable function ϕ on［0，+∞）as

In fact，

and for s＞0，

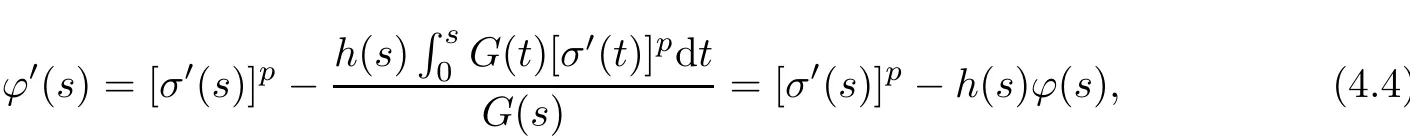
then

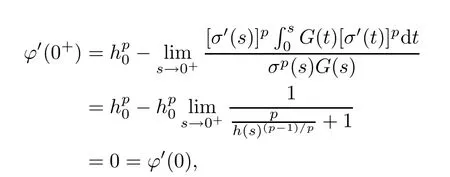
which implies that ϕ is continuous and differentiable on［0，+∞）.Moreover，we have

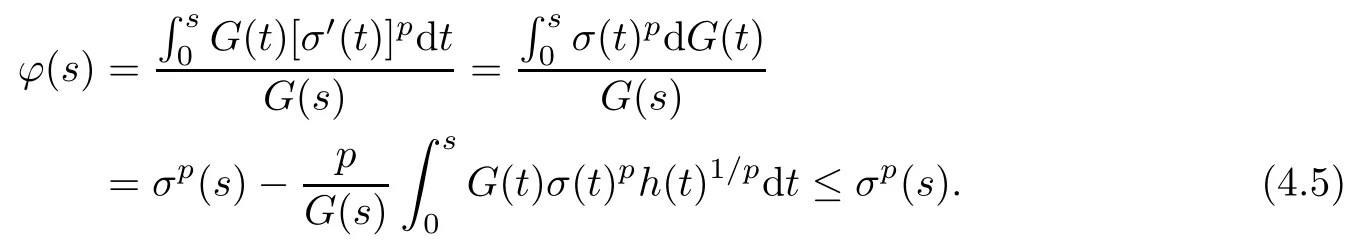
It follows from（4.4）and（4.5）that ϕ，ϕ′are bounded in［0，+∞），then takeL∞（Ω）as a test function in（1.1），we have

We deduce from（4.3），（4.4）and（4.5）that

which is a contradiction with λ1（f）＞1.□

By applying Theorem 4.1，we have the following result.

Corollary 4.2 Suppose 0≤f∈Lr（Ω）with r＞N/p and f/≡0.If either α＞p or α=p and λ1（f）＞1，then problem（3.17）does not have any positive solution in

Proof If u∈W1，p0（Ω）is a positive solution of（3.17），let R＞0 and v=Ru，then v∈W1，p0（Ω）satisfies

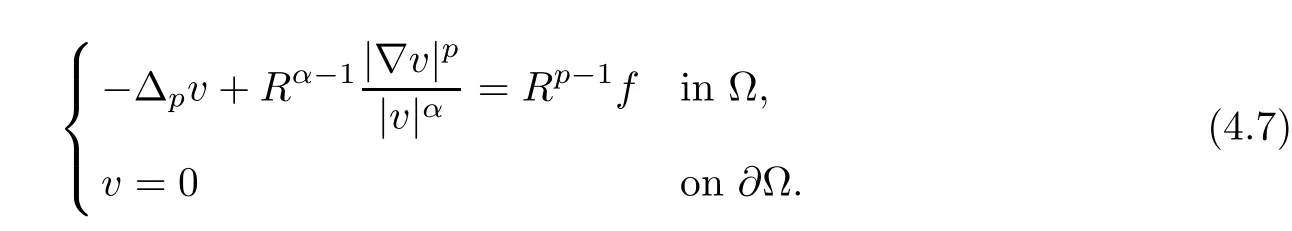
Set h（s）=Rα-1|s|-α，then h satisfies（4.1）.If α＞p，then

As λ1（Rp-1f）=λ1（f）/Rp-1and λ1（f）is positive（see［28］），it follows that there exists R0＞0 such that λ1（f）/Rp-1＞1 for any R∈（0，R0）.Therefore，we conclude by Theorem 4.1 that（4.7）does not admit positive solution in W1，p0（Ω）.

If α=p，then

Thus，h satisfies（4.2）with h0≥0，if and only if R≥1，and Theorem 4.1 implies the nonexistence of solutions to（4.7）provided that λ1（Rp-1f）=λ1（f）/Rp-1＞1.Let R=1，we conclude that（3.17）does not admit positive solution in W1，p0（Ω）if λ1（f）＞1. □

［1］Abdellaoui B，Dall'Aglio A，Primo I.Some remarks on elliptic problems with critical growth on the gradient. J Differ Equ，2006，222（1）:21-62

［2］Bensoussan A，Boccardo L，Murat F.On a nonliner PDE having natural growth terms and unbounded solutions.Ann Inst H Poincar´e Anal Non Lin´eaire，1988，5:347-364

［3］Boccardo L，Gallou¨et T.Strongly nonlinear elliptic equations having natural growth terms and L1data. Nonlinear Anal，1992，19:573-579

［4］Boccardo L，Murat F，Puel J P.Existence de solutions non borness pour certaines´equations quasi-lin´eaires. Port Math，1982，41:507-534

［5］Boccardo L，Murat F，Puel J P.Existence of bounded solutions for nonlinear elliptic unilateral problems. Ann Mat Pura Appl，1988，52:183-196

［6］Boccardo L，Murat F，Puel J P.L∞estimates for some nonlinear elliptic partial differential equations and application to an existence result.SIAM J Math Anal，1992，2:326-333

［7］Boccardo L，Segura de Le´on S，Trombetti C.Bounded and unbounded solutions for a class of quasi-linear elliptic problems with a quadratic gradient term.J Math Pures Appl，2001，80:919-940

［8］Ferone V，Murat F.Nonlinear problems having natural growth in the gradient:an existence result when the source terms are small.Nonlinear Anal，2000，42:1309-1326

［9］Ferone V，Posteraro M R，Rakotoson J M.L∞-Estimates for nonlinear elliptic problems with p-growth in the gradient.J Inequal Appl，1999，3:109-125

［10］Grenon N，Trombetti C.Existence results for a class of nonlinear elliptic problems with p-growth in the gradient.Nonlinear Anal，2003，52:931-942

［11］Maderna C，Pagani C D，Salsa S.Quasilinear elliptic equations with quadratic growth in the gradient.J Differ Equ，1992，97（1）:54-70

［12］Porretta A.Nonlinear equations with natural growth terms and measure data.2002-Fez Conference on Partial Differential Equations，Electron.J Diff Eqns Conf，2002，9:183-202

［13］Porretta A，Segura de Le´on S.Nonlinear elliptic equations having a gradient term with natural growth.J Math Pures Appl，2006，85:65-492

［14］Segura de Le´on S.Existence and uniqueness for L1data of some elliptic equations with natural growth. Adv Diff Equ，2003，9:1377-1408

［15］Trombetti C.Non-uniformly elliptic equations with natural growth in the gradient.Potential Anal，2003，18:391-404

［16］Arcoya D，Barile S，Mart´ınez-Aparicio P J.Singular quasilinear equations with quadratic growth in the gradient without sign condition.J Math Anal Appl，2009，350:401-408

［17］Arcoya D，Carmona J，Mart´ınez-Aparicio P J.Elliptic obstacle problems with natural growth on the gradient and singular nonlinear terms.Adv Nonlinear Stud，2007，7:299-317

［18］Arcoya D，Mart´ınez-Aparicio P J.Quasilinear equations with natural growth.Rev Mat Iberoamericana，2008，24:597-616

［19］Arcoya D，Carmona J，Leonori T，Mart´ınez-Aparicio P J，Orsina L，Petitta F.Existence and nonexistence of solutions for singular quadratic quasilinear equations.J Differ Equ，2009，246:4006-4042

［20］Leoni F.Nonlinear elliptic equations in RNwith absorbing zero order terms.Adv Diff Equ，2000，5:681-722

［21］Leray J，Lions J L.Quelques r´eultats de Vi˘sik sur les probl`emes elliptiques non lin´eaires par les m´ehodes de Minty-Browder.Bull Soc Math France，1965，93:97-107

［22］V´azquez J L.A strong maximum principle for some quasilinear elliptic equations.Appl Math Optim，1984，12:126-150

［23］Serrin J.Local behavior of solutions of quasi-linear equations.Acta Math，1964，111:247-302

［24］Tolksdorf P.Regularity for a more general class of quasilinear elliptic equations.J Differ Equ，1984，51: 126-150

［25］B´enilan P，Boccardo L，Gallou¨et T，Gariepy R，Pierre M.An L1-theory of existence and uniqueness of nonlinear elliptic equations.Ann Sc Norm Super Pisa Cl Sci，1995，22:241-273

［26］Boccardo L，Murat F.Almost everywhere convergence of the gardients of solutions to elliptic and parabolic equations.Nonlinear Anal，1992，19:581-597

［27］Stampacchia G.´Equations Elliptiques du Second Order`a Coefficients Discontinus.Montr´eal Les Press de I'Universit´e de Montr´eal，1966

［28］Xuan B.The eigenvalue problem for a singular quasilinear elliptic equation.Electron J Diff Eqns，2004，16:1-11

∗Received April 8，2014；revised April 25，2015.This research is supported by the Natural Science Foundation of Henan Province（15A110050）.

with 1＜p＜∞，where f is a positive measurable function which is bounded away from 0 in Ω，and the domain Ω is a smooth bounded open set in RN（N≥2）.Especially，under the condition that g（x，s）=1/|s|α（α＞0）is singular at s=0，we obtain that α＜p is necessary and sufficient for the existence of solutions into problem（0.1）when f is sufficiently regular.