魏正元，赵瑜，张鑫

（重庆理工大学数学与统计学院，重庆400054）

跳稳健积分波动率估计量的研究

魏正元，赵瑜，张鑫

（重庆理工大学数学与统计学院，重庆400054）

度量和预测资产价格的波动在金融计量学的多个领域起着关键的作用，为了更深刻地理解金融市场，基于高频金融数据的波动率研究更具有价值和意义。基于已实现方法与最邻近截尾的思想，构建了积分波动率的一种新的估计量——三项最小值已实现波动（TMinRV）。在模型假设下，证明了该估计量的相合性及跳存在情况下所遵循的渐近极限理论。实证研究选取上证综指和深证成指5分钟高频金融数据对TMinRV进行研究，并且将其与MinRV和MedRV进行对比，发现TMinRV能够更好地消除价格跳跃带来的波动，TMinRV的有效性及稳健性优于MinRV和MedRV，它能够更加准确地估计金融资产收益的波动。

高频金融数据；TMinRV；积分波动率；稳健性

波动率是进行资产定价、风险管理、投资组合选择等的基础，波动率研究一直是金融计量学多个领域研究的起点、基础和核心工作。对于低频金融时间序列，多采用ARCH类模型和SV类模型对波动率进行研究，而高频金融时间序列由于包含了更多的市场信息，基于高频金融数据的波动率研究更具有价值。Andersen和Bollerslev等在此方面做出了开创性的贡献，他们提出了一种全新的波动率度量方法——“已实现”波动（realized volatility，RV），其具有无模型、计算简便，并且在一定条件下是积分波动的无偏估计量［1］等优点。受“已实现”波动思想的启发，学者们对“已实现”波动率估计量不断进行改进和扩展，提出了其他“已实现”类波动率估计量，如“已实现”极差波动（realized range-based volatility，RRV）［2］，“已实现”双/三/多幂变差（realized bipower/tripower/mutipower variation，RBV/RTPV/RMPV）［3-5］等，其中RBV、RTPV、RMPV克服了RV不稳健性的缺点。国内方面，张世英［6-8］等考虑到日历效应的影响，提出了赋权的“已实现”波动/双幂变差/极差（WRV/WRBV/WRRV）。Andersen et al.（2012）［9］分别在RBV、RTPV的基础上提出了较之具有更好有效性和稳健性的最小值已实现波动率（MinRV）和中位数已实现波动率（MedRV）。

本文提出了三项最小值已实现波动率（TMinRV），通过近似地尺度化3个连续日内绝对收益率的最小值的平方而达到了跳稳健性，同时证明了该估计量是积分方差的相合估计量，并且得到了相应的渐近分布理论。通过对上证综指和深证成指的实证研究表明，TMinRV比MinRV和MedRV更加稳健。

1　TM inRV估计量

假设X=｛X｝0≤t≤1是一个定义在带滤子的概率空间（Ω，F，（Ft）t≥0，P）上的一维的连续时间对数价格过程，满足下述随机微分方程

其中μ是一个局部有界的可料过程，σ是一个适应的càdlàg（右连续，左极限存在）有界大于0的随机过程，W是标准布朗运动，是有限纯跳过程，κj表示跳跃的大小，L是计数过程。Xt在一个单位交易日［0，1］上的N+1个等距离散点0≤t0＜t1＜…＜tN≤1上观测，相应的收益率和时间区间分别表示为ΔXi=Xti-Xti-1和Δti=ti-ti-1，i=1，2，…，N。

金融资产收益率的波动一般是通过X的二次变差的连续部分来实现的，即积分波动率

在一般情况下，通常取时间区间为［0，1］，即给定的某一天。

1.1TM inRV的定义

受Andersen et al.（2012）［9］思想的启发，本文通过3个连续日内绝对收益率最小值的平方来定义积分波动率的一种新的相合的跳稳健估计量，首先给出如下定义。

定义三项最小值已实现波动（third minimum realized volatility）定义为

TMinRV估计量的相合性和跳稳健的直观性很明显，如果ΔXi-1，ΔXi，ΔXi+1～i.i.d.N（0，1），则

1.2 TM inRV的相合性和渐近分布理论

假设X在区间［0，1］上N+1个等时间间隔点观测，第i个观测值表示为Xi/N，i=0，1，…，N。相应的对数收益率表示为ΔNiX=Xi/N-Xi-1/N，i=1，2，…，N。我们引入长度为M（M≥1）的非重叠收益率区块，

则样本有K=N/M个这样的区块。

定义变量

令函数f∶R3R+且

则对于任何两个三维向量x⇀=（x1，x2，x3），y⇀=（y1，y2，y3），及常数C，有

由以上说明可将IV的TMinRV估计量写作

为了给出并证明TMinRV的相合性及渐近分布理论，继续作如下说明，令

由Burkholder-Davis-Grundy不等式有

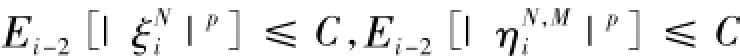
其中p＞0，C是一个正的常数，在本文不同处代表不同的值。

现将IV的基本估计量分解为条件期望和不同鞅序列的和

其中：

假设1令Xt是对数价格过程并假设其服从一个Brownian半鞅

其中μ，σ同上文所述，且进一步假设函数μ，σ是一致有界的，inft＞0σt＞0。

假设2假设波动过程服从广义Itô过程，即

证明首先证明引理1的第一部分，令

从而

由于

所以

事实上式（9）右边第一项是依概率收敛于0的，由式（7）可知

结合Cauchy-Schwartz不等式和Jensen不等式，当N→∞时，

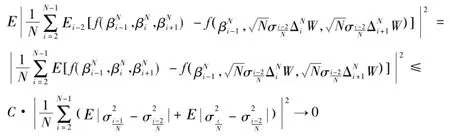
由上述收敛可知，当N→∞时，

为了证明此引理的第二部分，需要更强的条件假设2成立，事实上

引理2若假设1成立，并且当N→∞时，H2N→—P0。

证明

又因为

所以

根据三角不等式及（7）式知，当N→∞时有

其中g（x）=x2，上式最后一步成立是文献［11］中的特殊情形。是显然的，由得到，进而得到，即当N→∞时

引理4若假设1成立，则当N→∞时，有R2N-H2N→—P0；若假设1和假设2同时成立，则当N→∞时，有。

证明要证引理的第一部分，只需证明其第二部分。令

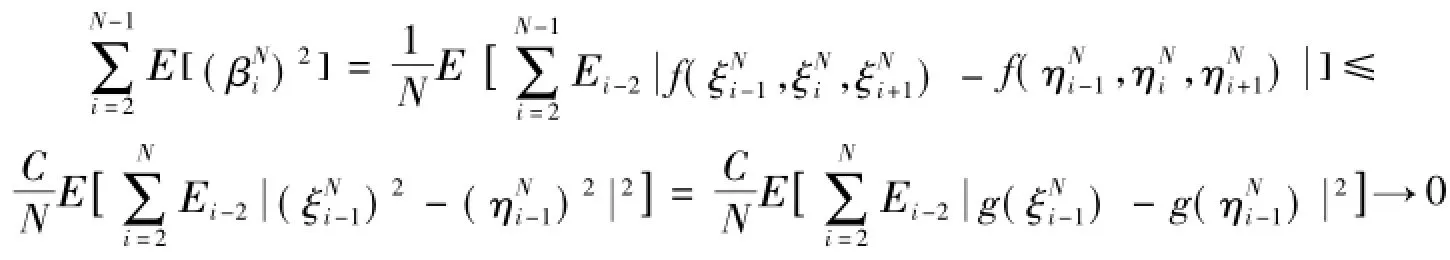
其中g（x）=x2，上式最后一步成立是文献［11］中的特殊情形。

即当N→∞时，

引理5若假设2成立，则当N→∞时，

其中γ=Var［f（V0，V1）］+2Cov［f（V0，V1），f（V1，V2）］，V0，V1，V2～i.i.d.N（0，1）。

证明将N个收益率观测等间隔地化分为K个区块，第K个向量记为，相应的渐近布朗运动观测向量为通过函数hM（·）∶RMR定义波动率的区块估计量

可通过Jacod and Shiryaev［12］中定理IX.7.28证明此引理。接下来只需说明定理IX.7.28的条件（7.27）—（7.31）成立：

最后，令｛Nt｝t∈［0，1］是W的有界半鞅，对于每个区块k，有

其中：γ=Var［f（V0，V1）］+2Cov［f（V0，V1），f（V1，V2）］，V0，V1，V2～i.i.d.N（0，1）。

下面我们分别通过两个命题给出TMinRV的相合性及渐近分布理论。

命题1假设对数价格过程Xt满足式（1），进一步假设其中μt是适应的、局部有界的，σt是适应的、左极右连的且inft＞0σt＞0，a.s.则当N→∞时，。

证明对RN作如下分解：RN=R1N+R2N=H1N+H2N+（R1N-H1N）+（R2N-H2N）。

命题2假设对数价格过程Xt满足式（1），进一步假设其中μt是适应的、局部有界的，σt是有界的，σt≠0且服从假设2所给出的Itô过程，则当N→∞时，

其中γ=Var［f（V0，V1）］+2Cov［f（V0，V1），f（V1，V2）］，V0，V1，V2～i.i.d.N（0，1）。

证明为了方便证明，首先作如下分解

由上述引理1，引理3～6知，当N→∞时，

并且，而其中γ代表常数。从而可知当N→∞时，

2　实证研究

本文选取2013.1.4—2013.12.31上证综指和深证成指5分钟间隔时间段的高频金融数据作为实证研究的样本，这期间共有238个交易日，共有238×51=12 138个数据。（数据从锐思数据库下载http：// www.resset.cn）

在上证综指5分钟时间间隔的对数价格序列中，找出相邻2个对数价格差绝对值最大的时间点为第5 585和5 586个时间点，可将其看作对数价格序列中的跳跃点，它对应第110天的第26个日内对数价格收益率。图1给出了［5 000，7 000］区间上的对数价格路径图，由图可见，在第5 585个时间点处发生了跳跃。图2给出了［105，120］区间上的TMinRV、MinRV和MedRV，其中折线代表TMinRV，星点代表Min-RV，圈点代表MedRV。由图可清晰地看出第110天的TMinRV明显小于MinRV和MedRV，说明TMinRV能更好地消除跳跃带来的波动。

对深证成指作类似于上证综指的分析，在第1 837和1 838个时间点相邻2个对数价格差绝对值最大，同样可看作对数价格序列中的跳跃点，对应第37天的第1个日内对数价格收益率。图3给出了［1500，3 000］区间上的对数价格路径图，由图可见，在第1 837个时间点处发生了跳跃。图4给出了［33，63］区间上的TMinRV、MinRV和MedRV，其中折线代表TMinRV，星点代表MinRV，圈点代表MedRV。由图可清晰地看出第37天的TMinRV明显小于MinRV和MedRV。

图1　上证综指5分钟数据部分对数价格路径图

图2　上证综指TMinRV与MinRV、MedRV部分图

图3　深证成指5分钟数据部分对数价格路径图

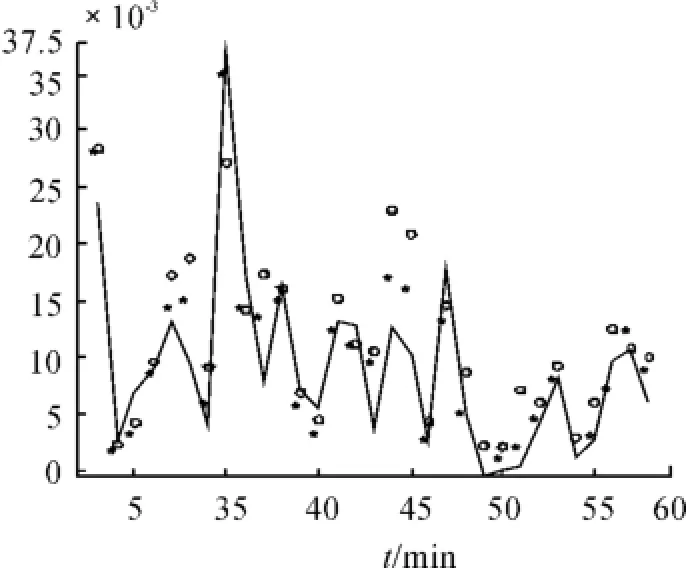
图4　深证成指TMinRV与MinRV、MedRV部分图

根据本文所定义的三项最小值已实现波动率（TMinRV）及Andersen et al［9］的最小值已实现波动率（MinRV）和中位数已实现波动率（MedRV）可以分别算出上证综指和深证成指对数收益率的上述3种估计量的描述性统计特征，如表1。

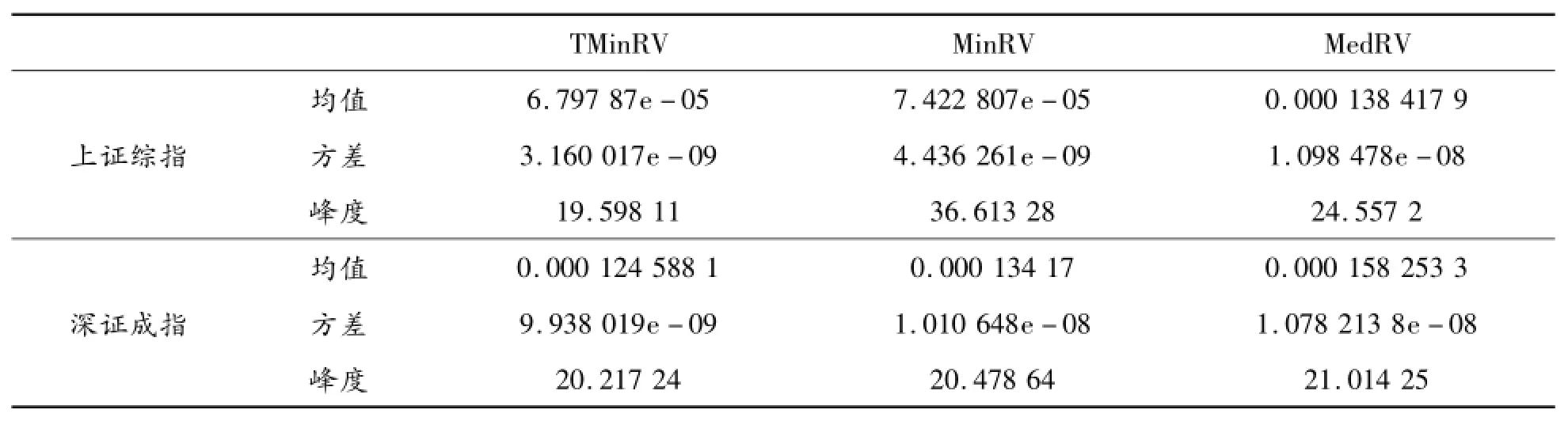
表1　TMinRV与MinRV及MedRV的描述性统计特征

由表1可知：首先，两种指数的TMinRV的均值和方差都比MinRV和MedRV小，说明TMinRV估计量较稳定，稳健性更好；其次，各样本的TMinRV的峰度均小于MinRV和MedRV的峰度，说明TMinRV的估计值的分布更加集中。

图5～8分别展现了上证综指和深证成指在2013年的238个交易日的TMinRV与MinRV，TMinRV与MedRV的对比图。由图可以直观地发现，无论是上证综指还是深证成指，从总体趋势而言TMinRV始终比MinRV和MedRV更加稳定。

图5　上证综指的TMinRV与MinRV

图6　上证综指的TMinRV与MedRV

图7　深证成指的TMinRV与MinRV

图8　深证成指的TMinRV与MedRV

3　总结及展望

本文采用非参数方法构建了三项最小值以实现波动（TMinRV），从理论和实证两方面对所提出的TMinRV的统计特征进行了理论证明和实证分析。理论方面首先给出了一系列引理，继而以定理的形式给出并且证明TMinRV是积分波动率的相合估计量，且服从渐近正态分布；实证方面通过对上证综指和深证成指2013.1.4—2013.12.31的5分钟高频金融数据研究表明所提出的TMinRV具有有效性及稳健性，是比MinRV和MedRV更优的积分波动率估计量，从而进一步证实了本文的理论结论。TMinRV不需要类似于GARCH的模型假设，可直接由观测的数据进行计算，计算简便操作性强，可以考虑将TMinRV拓展为赋权三项最小值已实现波动，亦可将最邻近截尾的理论方法拓展到一般的积分幂变差的估计量，这些工作有待进一步深入研究。

［1］Andersen TG，Bollerslev T，Diebold F X，et al.Exchange rate returns standardized by realized Volatility are（Nearly）Gaussian［J］.Multinational Finance Journal，2000，4：159-179.

［2］Christensen K，Podolskij M.Realized range-based estimation of integrated variance［J］.Journal of Econometrics，2007，141（2）：323-349.

［3］Guangying Liu，Xinsheng Zhang.Power variation of fractional integral processeswith jumps［J］.Statistics&Probability Letters，2011，81（8）：962-972.

［4］Mykland PA，Shephard N，Sheppard K.Econometric analysis of financial jumps using efficient bipower variation［R］.Working paper，Oxford-Man Institute，University of Oxford，2010.

［5］Mykland PA，Zhang L.Inference for continuous semimartingales observed at high frequency［J］.Econometrica，2009，77（5）：1403-1445.

［6］郭名媛，张世英.赋权己实现波动及其长记忆性、最优频率选择［J］.系统工程学报，2006，21（6）：568-573.

［7］李胜歌，张世英.金融波动的赋权“己实现”双幂次变差及其应用［J］.中国管理科学，2007，15（5）：9-14.

［8］唐勇，张世英.金融高频数据的加权己实现极差波动及其实证分析［J］.系统工程，2006，24（8）：52-57.

［9］Andersen TG，Bollerslev T，Diebold F X，et al.Jump-robust volatility estimation using nearest neighbor truncation［J］.Journal of Econometrics，2012，169（1）：75-93.

［10］Barndorff-Nielsen O E，Graversen SE，Jacod J，etal.A central limit theorem for realised power and bipower variations of continuous semimartingales［M］.Berlin：Springer，2006.

［11］Shephard N，Barndorff-Nielsen O E，Graversen SE，etal.Limit theorems for bipower variation in financial econometrics［J］.E-conometric Theory，2006，22（4）：677-719.

［12］Jacod J，Shiryaev A N.Limit theorems for stochastic processes.In：Grundlehren Der Mathematischen Wissenschaften［M］.Berlin：Springer，2003.

（责任编辑陈艳）

Study of Jum p-Robust Integrated Volatility Estim ation

WEIZheng-yuan，ZHAO Yu，ZHANG Xin
（School of Mathematics and Statistics，Chongqing University of Technology，Chongqing 400054，China）

Measuring and forecasting the volatility of financial asset returns plays a very important role in many areas of financial econometrics.To understand the financialmarket deeply，it is valuable and meaningful to study volatility based on high frequency financial data.We provided a novel jump-robust estimator of integrated variance based on the realized method and the theory of nearest neighbor truncation which is named third minimum realized volatility（TMinRV）.Under the model assumption，we proved the robustness and an asymptotic limit theory in the presence of jumps.By selecting the fiveminutes high frequency financial data of ShanghaiComposite index and Shenzhen Component index，empirical analysis on the statistical property of TMinRV shows that TMinRV can eliminate the influence of price jumpsmore effectively and estimate asset return volatilitymore steady.

high-frequency financial data；third minimum realized volatility（TMinRV）；integrated volatility；jump robustness

O21

A

1674-8425（2015）06-0134-10

2015-02-11

重庆市自然科学基金资助项目（cstc2012jjA00018）；重庆市教委科学技术研究项目（KJ130810）；重庆市高等教育教学改革研究项目（1203053）

魏正元（1975—），男，博士，副教授，主要从事应用概率统计、金融统计、金融数学研究。

魏正元，赵瑜，张鑫.跳稳健积分波动率估计量的研究［J］.重庆理工大学学报：自然科学版，2015（6）：134 -143.

format：WEI Zheng-yuan，ZHAO Yu，ZHANG Xin.Study of Jump-Robust Integrated Volatility Estimation［J］. Journal of Chongqing University of Technology：Natural Science，2015（6）：134-143.