陈 琦，王中原，常思江，舒敬荣

（1．南京理工大学能源与动力工程学院，江苏南京210094；2．陆军军官学院二系，安徽合肥230031）

求解非光滑最优控制问题的自适应网格优化

陈 琦1，王中原1，常思江1，舒敬荣2

（1．南京理工大学能源与动力工程学院，江苏南京210094；2．陆军军官学院二系，安徽合肥230031）

针对传统直接配点法在求解非光滑最优控制问题时存在离散误差大、精度低的问题，提出了一种自适应直接配点法。利用局部分段插值多项式逼近最优解，将最优控制问题离散为非线性规划问题，并给出了离散误差估计方法，根据离散误差的大小确定区间内节点的加密量，提出了自适应网格优化算法，利用该算法将大部分节点配置在非光滑区域以降低离散误差。最后通过仿真算例将所提算法与传统直接配点法和文献中的拟谱自适应算法分别进行比较，验证了所提算法的高精度和有效性。

最优控制问题；非光滑；直接配点法；网格优化；自适应算法

0 引 言

近年来，最优控制问题的求解引起了人们的广泛关注，在实际的应用中，许多最优控制问题往往是不光滑的，例如状态受约束的非对称航天器最优控制问题［1］、月球着陆问题［2］、桥式吊车最优控制问题［3］等。在文献［1］研究的非对称航天器最优控制问题中，原本光滑的最优解在对其中一个角速度施加不等式约束后，相应的控制力矩会出现不光滑现象。文献［2］研究了在月球着陆过程中的燃料最优控制问题，其数值仿真表明，在存在推力约束的条件下，控制量会存在切换现象。文献［3］研究了桥式吊车的最优控制问题，由于对控制量施加了上下界约束，导致最终的状态量不光滑且控制量不连续。

针对非光滑最优控制问题，国内外学者进行了大量的研究，并提出了较多的方法。文献［4－5］提出了hp自适应伪谱法，设计了一种多重区间分解策略，通过判断离散误差的分布情况，来确定区间分割点位置及子区间内的配点数。文献［6］采用hp自适应伪谱法研究了无人作战飞机的轨迹规划问题。文献［7］同样以hp自适应伪谱法为基础对N脉冲轨道进行了优化设计。为了进一步提高hp自适应伪谱法对非光滑问题的求解效率，文献［8］提出了分段点最佳化思想，提高了分段点收敛至不光滑点的速度。文献［9］以Chebyshev伪谱法为基础，引入方波脉冲函数，提出了一种复合Chebyshev有限差分法，该算法具有使用方便、精度高等优势。文献［10］提出了一种分段拟谱法，通过设置分点，将时间区域在非光滑区域进行划分，获得了较高的求解精度。文献［11］以Chebyshev伪谱法为基础提出了一种自适应算法，通过计算相邻2个配置点上数值解导数之差，来确定新分点的位置，从而提高了算法的精度。上述方法针对求解非光滑问题所做的改进均以伪谱法为基础，伪谱法作为一种全局离散方法，存在诸如微分矩阵计算量大、离散后的非线性规划问题（nonlinear programming problem，NLP）的雅克比矩阵较为稠密等缺点［12－13］，且随着节点数目的增加，这些缺点会更加突出。相比于伪谱法，直接配点法作为一种局部离散方法，其本身无需计算微分矩阵，主要采用分段插值多项式近似状态变量和控制变量，因此离散后的NLP规模很小，雅克比矩阵也更为稀疏，求解效率很高［12－13］，近年来得到了广泛的应用［14－17］。但该方法的计算精度低于伪谱法，且精度降低在求解非光滑最优控制问题时更为突出。若能对该方法进行改进，在保证计算效率高的同时，尽可能地降低离散误差，使其具有和伪谱法相当的计算精度，那么对于扩大该算法的使用范围将非常有意义。

有关直接配点法的改进，文献［18－19］提出了密度函数法，以密度函数来量化状态量和控制量的剧烈变化程度，并以此为基准重新分配离散节点。在密度函数选取合适的条件下，该方法可较快地将非光滑区域进行节点加密。然而针对不同的问题，选取合适的密度函数并不容易。文献［20－21］均以小波多尺度分析的方法构建了相应的节点调整策略。该方法主要以小波系数的幅值来确定非光滑区域，基于小波系数和二分点的对应关系，确定下一次迭代步所使用的节点并进行序列优化。与以上方法类似，本文也是通过调整离散节点的位置来提高求解精度。但在非光滑区域位置的确定方式上，不同于密度函数或是小波系数的方法，本文给出了一种离散误差的估计公式，然后根据该公式得到的离散误差的大小来确定非光滑区域的位置，构造了一种自适应网格更新策略，使节点能够根据离散误差的大小自动调整，从而避免了密度函数的挑选以及较为复杂的小波推导过程，在保证计算效率的基础上，提高了直接配点法对非光滑最优控制问题的求解精度，以期为求解非光滑最优控制问题提供一种新的思路。最后通过数值仿真并与文献中其他算法的对比验证了所提算法的准确性和有效性。

1 直接配点法

考虑一般Bolza型最优控制问题：

式中，状态变量x（t）∈Rn；控制变量u（t）∈Rm；f为动力学函数；e为终端约束函数；h为路径约束函数；t0和tf分别为初始和终端时间；Φ为终端性能指标函数；L为性能指标被积函数。

在区间［t0，tf］内，将连续的时间等分为N段，三阶Hermite－Simpson方法通过构造3次插值多项式近似子区间内的状态变量，记第k个子区间为［tk，tk＋1］（k＝0，1，…，N－1），该区间内的3次插值多项式可表示为

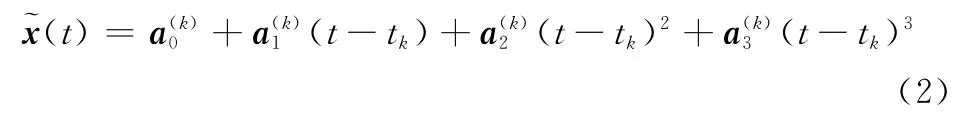
边界条件为

记hk＝tk＋1－tk，fk＝f［x（tk），u（tk），tk］，fk＋1＝f［x（tk＋1），u（tk＋1），tk＋1］，Hermite－Simpson方法还需要利用区间中点处的信息，为此令利用边界条件及区间中点处的导数信息，可得

从式（4）解出a（k）0，a（k）1，a（k）2和a（k）3并带入到式（2）

将tk＋1处的边值条件带入式（5）

记xk＝x（tk），xk＋1＝x（tk＋1），由式（6）可得

式（7）即为Hermite－Simpson defect向量，该向量构成了离散形式的系统微分方程约束。令，其中，式（1）中性能指标函数中的积分项利用复合Simpson公式求解，这样连续的最优控制问题式（1）便可在节点处转换为离散格式为

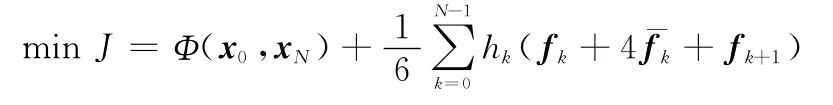
式中，k＝0，…，N－1。从式（8）可看出，连续的无限维最优控制问题被离散为一般的NLP问题，对于该问题，可采用非线性最优化算法进行求解。此外，在转换过程中加入了一个松弛因子δ，该因子的引入在一定程度上保证了离散后的NLP问题可行解的集合是非空的。

由于直接配点法将时间区域进行了N等分，因此便产生了均匀分布的离散节点，这些节点不会根据离散信息而改变，当最优控制问题在某些区域内变化剧烈甚至产生不光滑现象时，这种均匀节点的配置方式将会产生较大的离散误差，如果能在这些区域内适当增加节点的数目，那么可有效地减小离散误差。

2 网格更新算法

2．1 离散误差的估计

节点更新算法需要利用离散误差的信息，然而在一般情况下，最优控制问题的解事先是未知的，因此离散误差的大小只能采用特殊的方法进行估计，本小节主要给出离散误差的估计公式。求解式（8）得到每个节点上的状态量xi及其导数值＝fi。为了充分利用节点上的数值及其导数信息，构造Hermite插值函数（t）近似状态量x（t），有

式中，Ns为节点个数；αi，βi（i＝1，2，…，Ns）为Hermite插值基函数。每个插值基函数为2 Ns－1次多项式，并满足如下条件［18］

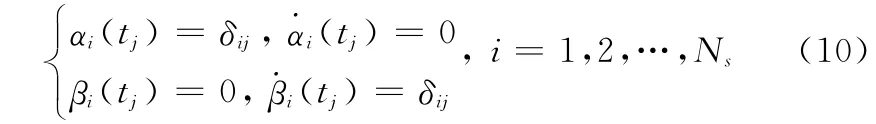
式中，Ci（t）为3次B－样条函数的基。

考虑区间［tk，tk＋hk］，根据系统微分方程，可知

式（13）的计算需要准确的状态量x（t）和控制量u（t），但这些均未知。为此，利用上文的和u）来近似求解x（tk＋hk），有

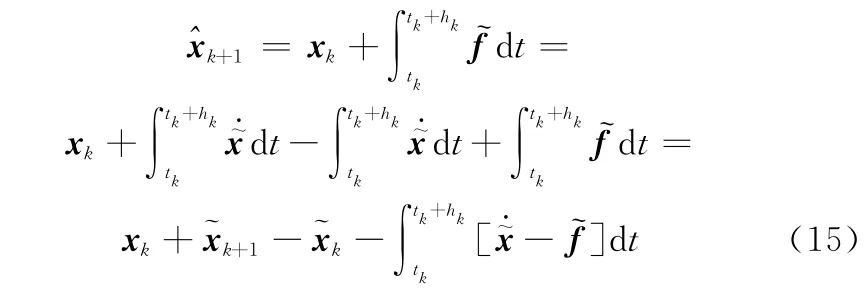
对式（16）两边取绝对值

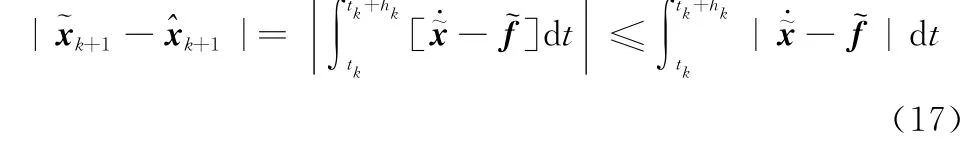
定义区间［tk，tk＋hk］上的绝对局部离散误差

式中

δi，k表示第i个状态量在第k区间内的离散误差。进而可定义最大相对局部离散误差

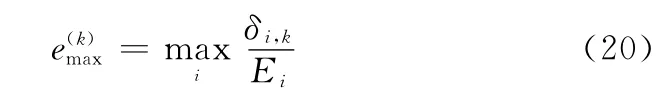
2．2 节点增加量的确定

设εtol为预先设定的误差阈值，且，那么需对第k个区间内的节点进行加密处理，设增加的节点数为M′k，增加节点后的离散误差为。为尽可能提高算法效率，令，因此得

式中，p为离散算法的计算精度。对于本文的Hermite－Simpson方法，对应p＝4．0［22］。求解式（21）可得区间k内需增加的节点数为

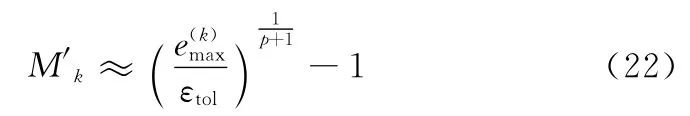
考虑到M′k为整数，且过大的M′k会使离散后的NLP产生稠密的雅克比矩阵，加剧求解难度，为此对M′k进行如下处理：

式中，M1为预先设定的常数，用于限制M′k的增长幅值。

2．3 自适应网格更新算法步骤

自适应网格更新算法步骤如下。

步骤1 初始化。给定正整数M0，M1，Nmaxiter以及Niter＝1；设置εtol的值，并在区间［t0，tf］内均匀布置M0个节点。

步骤2 求解NLP问题。采用直接配点法在节点上离散最优控制问题式，得到NLP问题，利用内点法（interior point optimization，IPOPT）［23］求解该问题，得到xN和uN。

步骤3 估计离散误差。根据式（9）和式（13），构造插值函数˜x（t）和˜u（t）近似xN和uN，结合式（18）～式（20）求解每个区间内的离散误差。

（2）节点更新次数未达到最大值，即Niter＜。

则根据式（23）计算M′k个节点加入到区间k中，否则不增加节点，循环本步操作以遍历k值。

3 数值验证

3．1 能量最优控制问题

为了验证本文所提算法的准确性，本小节采用该算法求解文献［24］中具有解析解的非光滑最优控制问题：

自适应直接配点法的计算参数取为M0＝5，M1＝5，＝10，εtol＝1×10－5，δ＝1×10－10。该最优控制问题的解析解为

由解析解可看出，控制量在t＝0．3和t＝0．7处出现不光滑现象。图1分别将自适应算法和采用均匀节点的传统直接配点法的数值计算结果与解析结果进行了对比，从中可以明显地发现，由自适应算法求解出的控制量在边界点及t＝0．3和t＝0．7点均能很好地逼近解析解，而传统直接配点法则产生了较大的误差。图2为状态变量的对比结果，可以发现在t＝0．3和t＝0．7附近，自适应算法配置了较多的节点，且节点处的状态变量的值与解析解十分吻合，而传统直接配点法则不能较好地逼近解析解。

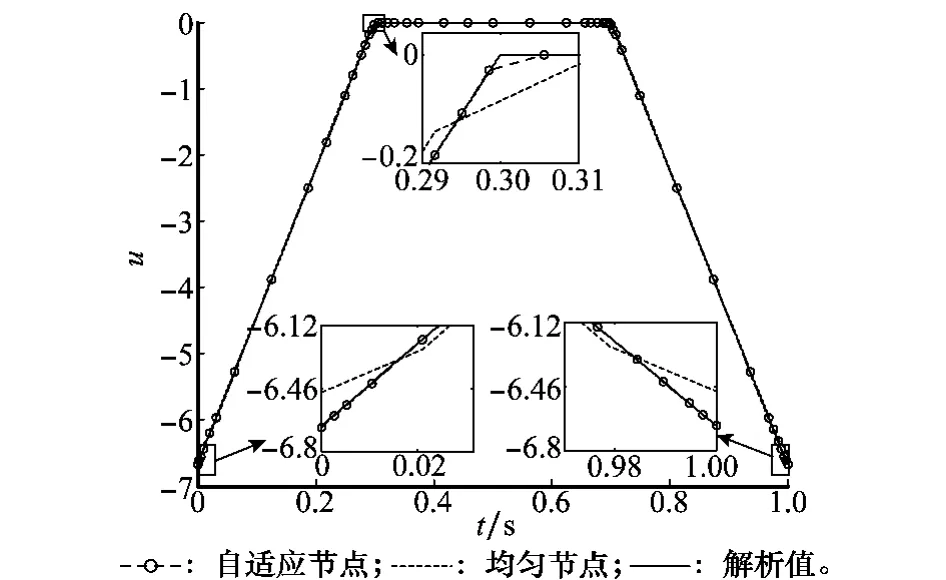
图1 控制量的数值解与解析解对比

图2 状态量的数值解与解析解的对比

图3为每步迭代过程中的节点配置情况，从中可以看出，自适应算法在迭代的过程中能够自动地增加两端及t＝0．3和t＝0．7附近的节点数目，对比图1可知，自适应算法所增加节点的位置正是传统算法不能较好逼近真值的区域，这说明自适应算法能够自动识别出离散误差较大的局域，并对其进行加密节点处理，这一措施可以有效地提高求解精度。图4对比了2种算法的收敛效果，从中可以看出，当节点数目为30时，自适应算法的最大离散误差为10－4，而传统算法的离散误差仍大于3×10－4，若使其误差接近当10－4，所需节点数为50个，但此时自适应算法的离散误差已经小于10－5，可见自适应算法的收敛速度要明显快于传统算法，并且随着节点数的增加，这种差异愈发明显。从以上分析可得出，在同样节点数目的情况下，通过合理地安排节点的配置可以有效地降低离散误差。以上的仿真对比结果验证了本文所提算法在处理非光滑最优控制问题时的准确性，这为今后算法的有效使用提供了依据。

图3 每步迭代过程中的节点配置

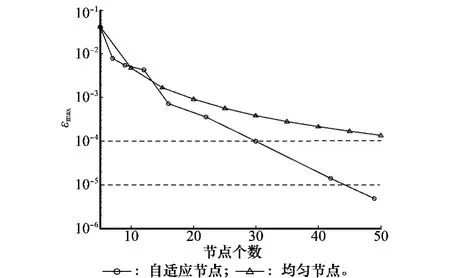
图4 算法收敛过程

3．2 航天器最优控制问题

选取文献［1］中的航天器最优控制问题，采用本文的算法进行求解有

式中，ω1（t），ω2（t）和ω3（t）为航天器角速度；I1，I2和I3为航天器转动惯量；u1，u2和u3为控制变量。计算参数εtol＝1×10－6，其他参数的选取与前文一致。

计算结果如图5～图9及表1所示。图5为状态量变化曲线，可见求解得到的结果满足约束条件，同时可看出，对ω1（t）施加约束后，自适应算法将大部分节点配置在靠近约束的区域。图6～图8为最优控制量变化曲线，为了验证本文算法的正确性，图中将自适应算法和传统算法求解的控制量分别与文献［1］中的结果分别进行了对比。从图6可看出，控制量u1在t＝40s附近产生了不光滑现象，自适应算法与传统算法所得的结果均能吻合文献［1］中的结果。图7和图8分别为u2和u3变化曲线，从中可以看出，自适应算法所得的结果与文献［1］中的结果相符，但是传统算法得到的结果则不能吻合文献［1］中的结果，产生了较大的偏差。由此验证了自适应算法的求解精度要高于传统算法。

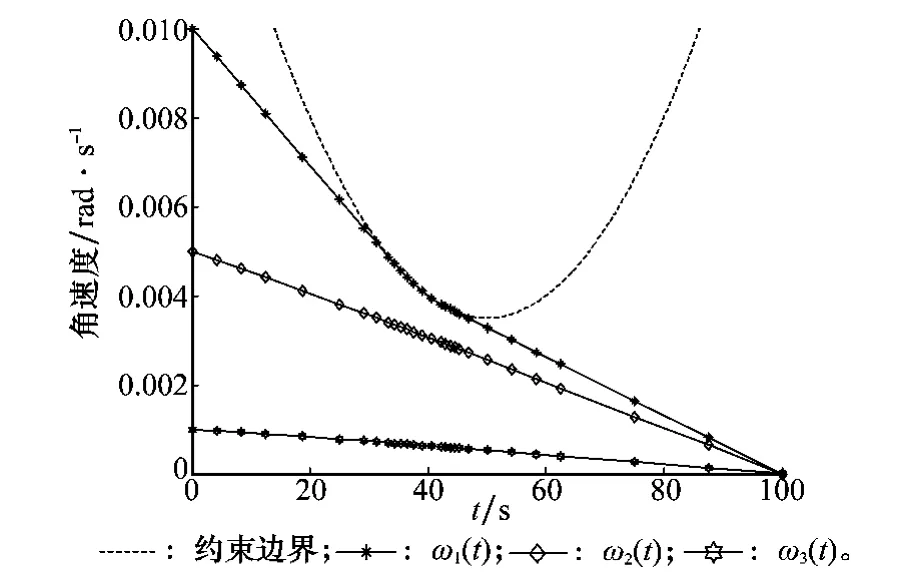
图5 状态变量变化曲线

图6 控制变量u1变化曲线

图7 控制变量u2变化曲线

图8 控制变量u3变化曲线

图9 自适应算法和传统算法计算误差对比（N＝28）

表1 本文算法与文献［11］算法对比

图9为在同样节点数目的情况下（28个），2种算法计算误差的对比曲线。可以看出，传统方法使用了均匀分布的离散节点，且在端点及t＝40s附近产生了较大的离散误差。而自适应算法采用非均匀的节点配置方式，将大部分节点设置在t＝40s附近，极大地降低了离散误差，从而验证了本文算法的高精度。

针对该航天器最优控制问题，文献［11］以自适应拟谱法进行了求解。为了进一步考察本文所提的自适应直接配点法在每步迭代过程中的性能，表1将本文方法在求解航天器最优控制问题时的每步迭代结果与文献［11］中的迭代结果进行了对比。从中可看出，本文算法需迭代7次，大于文献［11］中的5次迭代，但所需的节点数目却由176个减小为28个，降低了84．1%，节点数目的降低有助于减小离散后的NLP的规模，从而提高优化求解效率。此外，从表1也可看出，在相同迭代次数时，本文方法得到的目标值要比文献［11］中得到的目标值大，这是由于虽然迭代过程中节点位置在不断地调整，数量也在不断地增加，但整体来讲其数量还是偏少的（迭代7步后节点数才达到17），位置也不是最优的，而且直接配点法本身的离散精度也要低于拟谱法。因此，在节点数目偏少且位置并非最优的情况下，其得到的目标值便大于文献［11］中得到的目标值。但是这种情况在后续的迭代中得到了改善，从表1中可看出，从第6步开始，随着节点数目的增加及节点位置的优化，目标值在不断减小，最终得到了比文献［11］更小的目标值，这表明了本文算法在求解精度上具有一定的优势。

4 结 论

本文对非光滑最优控制问题的数值解法进行了研究，提出了一种自适应直接配点法。通过构造分段多项式近似状态变量和控制变量，将最优控制问题离散为非线性规划问题，并给出了离散误差的估计方法及节点加密量的计算公式，根据离散误差的大小自适应地配置节点。该算法能够自动地确定出最优控制问题中的非光滑区域，并对其进行加密处理，能较好地解决传统直接配点法计算精度有限、收敛速度过慢等问题。此外，通过将数值算例的结果与已有文献中的拟谱自适应算法进行比较，验证了所提算法仅需较少的节点便可获得相当的计算精度。本文算法具有一定的通用性，可为此类问题的求解提供参考。

［1］Jaddu H．Direct solution of nonlinear optimal control problems using quasi linearization and Chebyshev polynomials［J］．Journal of the Franklin Institute，2002，339（4／5）：479－498．

［2］Shamsi M．A modified pseudospectral scheme for accurate solution of bang－bang optimal control problems［J］．Optimal Control Application and Methods，2011，32（6）：668－680．

［3］Ross I M，Fahroo F．A direct method for solving nonsmooth optimal control problems［C］∥Proc．of the International Federation of Automatic Control World Conference，2002：3860－3864．

［4］Darby C L，Hager W W，Rao A V．An hp－adaptive pseudospectral method for solving optimal control problems［J］．Optimal Control Application and Methods，2010，32（4）：476－502．

［5］Darby C L，Hager W W，Rao A V．Direct trajectory optimization using a variable low－order adaptive pseudospectral method［J］．Journal of Spacecraft and Rockets，2011，48（3）：433－445．

［6］Liu H M，Ding D L，Huang C Q，et al．UCAV low observable attacking trajectory planning based on adaptive pseudospectral method［J］．Systems Engineering and Electronics，2013，35（1）：78－84．（刘鹤鸣，丁达理，黄长强，等．基于自适应伪谱法的UCAV低可探测攻击轨迹规划研究［J］．系统工程与电子技术，2013，35（1）：78－84．）

［7］Han W H，Yang X，Jiang M Z．Optimal design of N－impulse trajectories based on hp－adaptive pseudospectral method［J］．Systems Engineering and Electronics，2013，35（12）：2566－2571．（韩威华，杨新，姜萌哲．基于hp自适应伪谱法的N脉冲轨道优化设计［J］．系统工程与电子技术，2013，35（12）：2566－2571．）

［8］Liu Y B，Zhu H W，Huang X N，et al．Optimal mesh segmentation algorithm for pseudospectral methods for non－smooth optimal control problems［J］．Systems Engineering and Electronics，2013，35（11）：2396－2399．（刘渊博，朱恒伟，黄小念，等．伪谱法求解非光滑最优控制问题的网格优化［J］．系统工程与电子技术，2013，35（11）：2396－2399．）

［9］Marzban H R，Hoseini S M．A composite Chebyshev finite difference method for nonlinear optimal control problems［J］．Communication in Nonlinear Science and Numerical Simula－

tion，2013，18（6）：1347－1361．

［10］Zhang W．A numerical method for solving nonsmooth optimal control problems［J］．Applied Mathematics Journal of Chinese Universities，2009，24（2）：207－220．（张稳．非光滑最优控制问题的一种数值解法［J］．高校应用数学学报，2009，24（2）：207－220．）

［11］Qin T H，Ma H P．Adaptive algorithm for weakly discontinuous solutions of optimal control problems［J］．Control and Decision，2013，28（2）：313－316．（秦廷华，马和平．最优控制问题弱间断解的一个自适应算法［J］．控制与决策，2013，28（2）：313－316．）

［12］Huntington G T，Rao A V．Comparison of global and local collocation methods for optimal control［J］．Journal of Guidance，Control，and Dynamics，2008，31（2）：432－436．

［13］Huntington G T，Rao A V．A Comparison between global and local orthogonal collocation methods for solving optimal control problems［C］∥Proc．of the AIAA American Control Conference，2007：1950－1957．

［14］Herman A L，Conway B A．Direct optimization using collocation based on high－order Gauss－Lobatto quadrature rules［J］．Journal of Guidance，Control，and Dynamics，1996，19（3）：592－599．

［15］Hull D G．Conversion of optimal control problems into parameter optimization problems［J］．Journal of Guidance，Control，and Dynamics，1997，20（1）：57－60．

［16］Tu L H，Yuan J P，Luo J J，et al．Lunar soft landing rapid trajectory optimization using direct collocation method［J］．Chinese Space Science and Technology，2008，（4）：19－24．（涂梁辉，袁建平，罗建军，等．基于直接配点法的月球软着陆轨道快速优化［J］．中国空间科学技术，2008，（4）：19－24．）

［17］Geiger B R，Horn J F，Delullo A M，et al．Optimal path planning of UAVs using direct collocation with nonlinear programming［C］∥Proc．of the AIAA Guidance，Navigation，and Control Conference and Exhibit，2006：1－13．

［18］Zhao Y M，Tsiotras P．A density－function based mesh refinement algorithm for solving optimal control problems［C］∥Proc．of the AIAA Infotech and Aerospace Conference，2009．

［19］Zhao Y M，Tsiotras P．Density functions for mesh refinement in numerical optimal control［J］．Journal of Guidance，Control，and Dynamics，2011，34（1）：271－277．

［20］Jain S，Tsiotras P．Trajectory optimization using multiresolution techniques［J］．Journal of Guidance，Control，and Dynamics，2008，31（5）：1424－1436．

［21］Feng Z W，Zhang Q B，Tang Q G，et al．Node adaptive refinement for trajectory optimization based on second－generation wavelets［J］．Journal of Aerospace Power，2013，28（7）：1659－1665．（丰志伟，张青斌，唐乾刚，等．基于二代小波的轨迹优化节点自适应加密［J］．航空动力学报，2013，28（7）：1659－1665．）

［22］Kress R．Numerical analysis［M］．New York：Wiley，1998．

［23］Wachter A，Biegler L T．On the implementation of a primaldual interior point filter line search algorithm for large－scale nonlinear programming［J］．Mathematical Programming，2006，106（1）：25－57．

［24］Benson D A．A Gauss pseudospectral transcription for optimal control［D］．Cambridge：Massachusetts Institute of Technology，2005．

E－mail：qiychan＠126．com

王中原（1958－），男，研究员，博士，主要研究方向为飞行器飞行控制理论与技术。

E－mail：zywang＠njust．edu．cn

常思江（1983－），男，讲师，博士，主要研究方向为弹箭飞行与控制技术。

E－mail：ballistics＠126．com

舒敬荣（1974－），男，讲师，博士，主要研究方向为外弹道学。

E－mail：shujr1974＠126．com

Adaptive mesh refinement for solving non－smooth optimal control problems

CHEN Qi1，WANG Zhong－yuan1，CHANG Si－jiang1，SHU Jing－rong2
（1．School of Energy and Power Engineering，Nanjing University of Science and Technology，Nanjing 210094，China；2．Department 2，Army Officer Academy of PLA，Hefei 230031，China）

Due to the large discrete errors and low accuracy of the conventional direct collocation method for solving non－smooth optimal control problems，an adaptive direct collocation method is presented．The optimal control problem is transcribed into a nonlinear programming problem by using local piecewise interpolation polynomials to approximate the optimal solution．The estimation method of discrete errors is also presented，and an adaptive mesh refinement algorithm is used to refine the grid by adding nodes to the segments in which the optimal solution is non－smooth，the algorithm is repeated until a user－specified error tolerance is met．Finally，the simulation results demonstrate the utility and efficiency of the proposed method by comparing it with the conventional direct collocation method and the adaptive pseudospectral algorithm respectively．

optimal control problem；non－smooth；direct collocation method；mesh refinement；adaptive algorithm

TP 273．1

A

10．3969／j．issn．1001－506X．2015．06．23

陈 琦（1989－），男，博士研究生，主要研究方向为飞行器轨迹优化、制导与控制。

1001－506X（2015）06－1377－07

2014－07－14；

2014－10－23；网络优先出版日期：2014－11－20。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141120．2110．009．html

国家自然科学基金（11272356）；中国博士后科学基金（2013M541676）资助课题