杨辉华，谢谱模，张晓凤，马 巍，刘振丙

（1.桂林电子科技大学 广西信息科学实验中心，广西 桂林541004；2.北京邮电大学 自动化学院，北京100876；3.桂林电子科技大学 电子工程与自动化学院，广西 桂林541004）

设计和决策问题需要对多个目标同时进行优化，而此类问题中的各个目标之间往往互相矛盾，需要在多个目标间进行折中.通常而言，多目标优化问题要难于单目标优化问题，在单目标优化问题中，一般可以在搜索空间找到一个全局最优解，而多目标优化问题中一般不存在使得多个目标同时最优的全局最优解.对于多目标优化问题，通过折中优化而得到的曲线或曲面，被称为Pareto前沿，针对多目标优化问题，求得一组分布良好的Pareto前沿.

Yang等［1］在2009年提出一种新的智能优化算法——布谷鸟搜索（cuckoo search，CS）算法，CS算法过去几年在很多领域，如工程设计、任务调度、背包问题、旅行商问题等取得了良好的优化效果［2-5］，被证明性能好于一些现有启发式算法，如PSO，GA.鉴于CS算法的简单和高效，LI等［6-9］提出相关改进算法.2011年，Yang等［10］在CS算法基础上提出了多目标布谷鸟搜索（multi-objective cuckoo search algorithm，MOCS）算法，自此该算法也开始受到人们的广泛关注［11-12］.在MOCS算法中Lévy飞行的步长控制量α0为固定值，原种群nest经Lévy飞行后得到新种群nest′，在nest和nest′上随机选取2个个体进行非支配关系的比较，然后基于比较结果进行个体的替换.本文在MOCS算法的基础上，对Lévy飞行的步长控制量α0，下一次迭代种群的选择方法进行改进，提出改进的多目标布谷鸟 搜 索 算 法（improved multi-objective cuckoo search algorithm，IMOCS），在 基 准 测 试 实 例SCH、ZDT 系 列、LZ 上 对 比IMOCS 与MOCS、NSPSO、NSGA-II的性能.

1 多目标优化问题的相关基本概念

一个多目标优化问题可表示如下：

式中：目标向量F（x）含有k个目标fi（x）；gi（x）为约束条件；Ω 为可行域；x 为n 维决策向量，x＝［x1，x2，…，xn］.

在一般情况下，多目标优化问题不存在使得所有目标同时最优的全局最优解，但是可以存在这样的解：对一个或者多个目标不可能进一步优化，而对其他目标不至于劣化，这样的解称为Pareto最优解.有关Pareto的相关定义如下：

定义1（Pareto支配）：对于目标向量u＝［u1，u2，…，uk］以及v＝［v1，v2，…，vk］，称uPareto支配v（记：u≺v），当且仅当∀i∈｛1 ，2，…，k｝ ：ui≤vi∧∃i∈｛1 ，2，…，k｝ ：ui＜vi.

定义2（Pareto最优解）：对于一个解x∈Ω，称x为Pareto最优解，当且仅当不存在x′∈Ω，使得v＝F（x′）＝［f1（x′），f2（x′），…，fk（x′）］支配

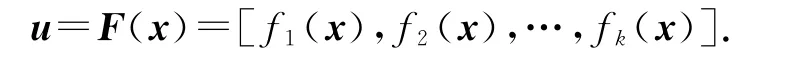
定义3（Pareto最优解集合）：对于一个给定的多目标优化问题，Pareto 最优解集合（P）的定义如下：

定义4（Pareto前沿）：对于一个给定的多目标优化问题，Pareto前沿（PF）的定义如下：

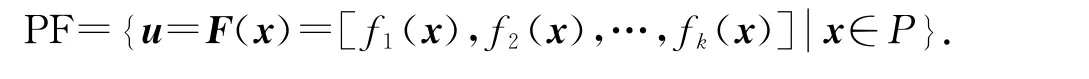
2 多目标布谷鸟搜索算法

在标准的MOCS［10］中，Lévy飞行表示如下：

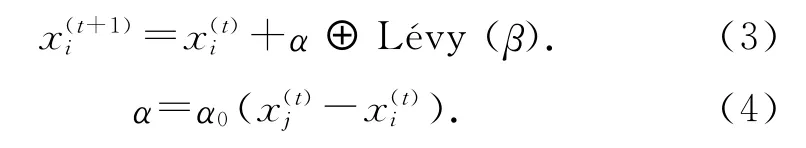
式中：α0为步长控制量，α 为步长，Lévy（β）为服从Lévy分布的随机步长，0＜β≤2为指数，xj（t）为在第t次迭代得到的结果中随机选择的一个不同于xi（t）的个体.MOCS算法描述如下：

3 改进的多目标布谷鸟搜索算法

3.1 动态自适应步长控制量

在标准MOCS中步长控制量α0为定值，当α0较小时，在迭代初期不利于全局搜索，当α0较大时，在迭代后期不利于局部搜索.基此，在IMOCS中对α0进行改进，研究动态自适应变化的α0对IMOCS性能的影响.

Rechenberg等［13］在研究进化计算的参数自动调整时提出了1／5原则，基于Rechenberg原则张永韡等［14］在研究布谷鸟搜索算法时提出一种α0动态自适应变化的方法.本文提出一种更加简单有效的α0动态自适应变化的方法，定义如下：

式中：K 为变化率，r为新解改善的比例，T 为阈值.K的取值大于0，T 的取值根据Rechenberg原则，一般取0.2～0.3之间.r的计算方法为新解中相比原个体GD值变小的个体的总数除以种群大小.当r的值大于T 时，K（r-T）为正数，使得exp（K（r-T））的值大于1，αt＋10相对于αt0增大，此时种群的搜索范围加大，趋于全局搜索；当r的值小于T 时，K（r-T）为负数，使得exp（K（r-T））的值小于1，αt＋10相对于αt0减小，此时种群的搜索范围减小，趋于局部搜索；当r的值等于T 时，K（r-T）为0，exp（K（r-T））的值为1，αt＋1等于αt，此时种群的搜索范围不变.对α0的值应限定在一定范围，防止过调.

3.2 非支配集排序

Srinivas等［15］在1994年提出了一种基于排序选择和小生境技术的非支配排序方法，并结合遗传算法提出了一种求解多目标优化问题的非支配遗传算法（NSGA）.之后Deb等［16］于2002年对NSGA中非支配排序层级的计算以及需要设定共享半径的适应度共享策略进行改进，提出了NSGA-II，在NSGA-II中非支配排序层级的计算时间复杂度更低，并且拥挤度距离的计算不需要人为设定参数，本文采用NSGA-II中非支配集排序的方法来计算每个个体的层级和拥挤度距离.

3.3 基于非支配排序选择种群

在MOCS中个体的选择是基于单个个体间的比较，即对种群nest中每个个体nestj，在新产生的种群nest′中随机选择一个个体nest′i，如果nest′i支配nestj，则 用nest′i替 换nestj.在IMOCS 中，将nest和nest′结合，组成包含2n 个个体的种群tempnest，对tempnest 进行非支配集排序，对tempnest中的每个个体i 增加2 个属性irank和idistance.从tempnest中选出n 个个体，首先选择层级较低的个体，若层级相同，则选择拥挤度较大的个体.

3.4 IMOCS算法描述

IMOCS算法描述如下：

4 实验仿真和分析

4.1 测试实例

为验证IMOCS的改进效果，选择广泛使用的6个测试实例SCH，ZDT 系列及LZ，说明如下：

1）SCH［17］，其Pareto前沿为凸状，

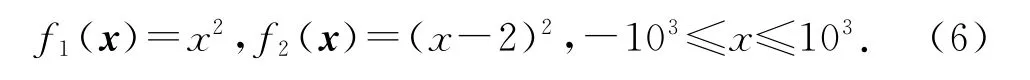
2）ZDT1［18-19］，其Pareto前沿为凸状，

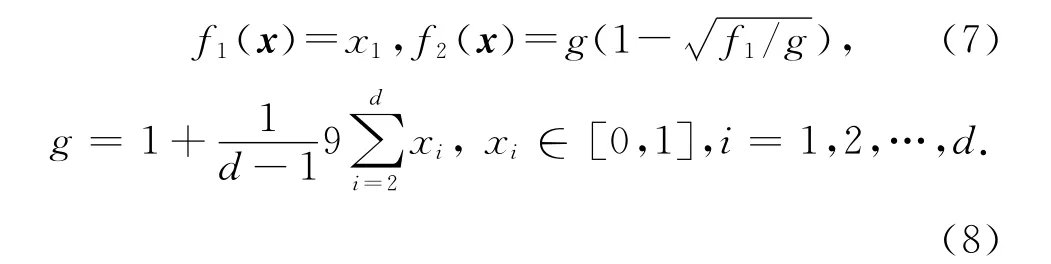
式中：d 为x 的维数.

3）ZDT2，其Pareto前沿为非凸状，

4）ZDT3，其Pareto前沿不连续，

对于ZDT3，在其真实Pareto前沿中，f1从0变化到0.852，f2从-0.773变化到1.

5）ZDT4［20-21］，有很多局部Pareto前沿，

6）LZ［20-22］，其Pareto前沿为凸状，

式中：J1＝｛j｜j为奇数并且2≤j≤d｝，J2＝｛j｜j为偶数并且2≤j≤d｝.

4.2 性能评价指标

为验证IMOCS的性能，实验中采用2个评价指标：广义距离（generational distance，GD）和所求Pareto前沿（P＊）的多样性Δ［23］.

GD 用于衡量所求P＊与真实前沿P 的接近程度，GD 越小，所求P＊越接近P，GD 定义如下：

式中：di为第i个个体与对应真实Pareto前沿之间的欧氏距离，p 为优化问题中的目标个数，对于2个目标的优化问题，p ＝2.

Δ 用于衡量P＊的多样性，定义如下：

4.3 参数说明

测试实例ZDT1，ZDT2，ZDT3中的维度d＝30，ZDT4中d＝10，LZ中d＝5.在IMOCS算法中发 现 概 率pa＝0.5 与MOCS［6］相 同，SCH，ZDT1，ZDT2，ZDT3的动态自适应变化α0初始值为0.1，变化率K＝1.07，阈值T＝0.3，α0限定在［0.01，2］；ZDT4，LZ 的动态自适应变化α0初始值为0.5，变化率K＝1.07，阈值T＝0.15，α0限定在［0.1，5］.以上参数的设置，α0的限定范围、变化率K、阈值T 由实验得出.

4.4 实验结果与讨论

本文在Pentium（R）Dual-Core T4300 ＠2.10GHz CPU，2GB RAM，Windows 7，MATLAB 2010b的计算环境下编程实现IMOCS 算法.为了减小数据随机性对测试结果的影响，更准确地反映算法性能，IMOCS算法在测试中都独立运行10次，然后计算GD 及Δ 的平均值与方差.

4.4.1 步长控制量对IMOCS性能的影响 为了验证步长控制量α0对IMOCS性能的影响，本文分别在α0固定不变（α0＝0.01）和α0动态自适应变化时对IMOCS的性能影响进行对比测试.设置n＝200，MaxIter＝100，如表1所示给出了6个测试实例的P＊与P 之间GD 的平均值GD和方差δ2，表2给出了P＊的Δ 的平均值和方差δ2.

从表1 中可以看出，动态自适应变化的α0相比取固定值时使得IMOCS具有更好的性能，所有测试实例Pareto前沿的较α0固定时都有减小，即当IMOCS中α0动态自适应变化时，其所求Pareto前沿更加接近真实Pareto前沿.且从表2中可以看出，当IMOCS中α0动态自适应变化时，其所求Pareto前沿的多样性也更好.

如图1所示给出了各测试实例的Pareto前沿.针对ZDT4，α0动态自适应变化下的IMOCS比α0固定下的IMOCS所求要小4个数量级，有很大的改进，这是由于固定α0下的IMOCS在10次独立运行中都未能搜索到全局Pareto前沿，而动态自适应变化α0下的IMOCS全部搜索到全局Pareto前沿，因而，这在ZDT4的Pareto前沿图中更加直观体现了这一点.

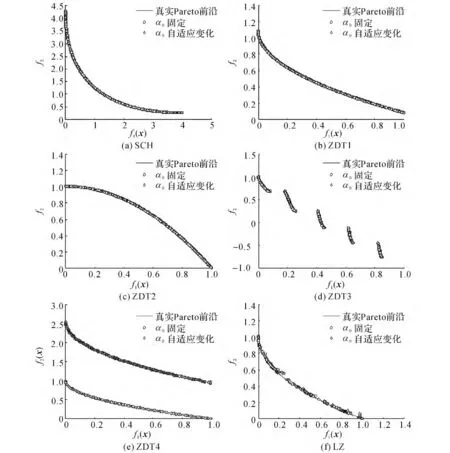
图1 6个测试实例的Pareto前沿Fig.1 Pareto fronts of six test instances

表1 步长控制量动态自适应变化时与固定不变时所求GD的均值和方差Tab.1 Mean and variance of GD under dynamic adaptive changing step-size control amount and fixed one

表2 步长控制量动态自适应变化时与固定不变时所求多样性的均值和方差Tab.2 Mean and variance of diversity under dynamic adaptive changing step-size control amount and fixed one

如图2所示给出了6个测试实例的GD 收敛曲线.针 对 只 有1 维 变 量 的SCH，2 类α0下 的IMOCS都收敛很快；对于ZDT1，ZDT2，ZDT3，动态自适应变化α0下的IMOCS比固定α0时收敛速度明显要快；对ZDT4，在30次迭代以前动态自适应变化α0下的IMOCS 所求GD 曲线在固定α0下的IMOCS所求GD 曲线之上，这主要是由于动态自适应变化α0下的IMOCS处于探索期，α0的变化幅度较大，而30次迭代以后动态自适应变化α0下的IMOCS所求GD 曲线在固定α0下的IMOCS所求GD 曲线之下，并且最终其GD 的数量级为10-5，在图1（e）中体现为动态自适应变化α0下的IMOCS达到了全局Pareto前沿，而固定α0下的IMOCS陷入了局部Pareto前沿，其最终的GD 数量级为10-2，从LZ 的收敛曲线图中可以看出，固定α0下的IMOCS在搜索中GD 值有几处明显的波动，而动态自适应变化α0下的IMOCS较稳定.由此可知：动态自适应变化α0能使IMOCS快速、稳定的收敛.

如图3所示为动态自适应变化的α0在1 000次迭代过程中的变化曲线，其测试实例为ZDT4.由图3可以看出，在40次迭代以前，α0的值有较大的波动，这是α0的一个自适应调整过程，算法处在探索期，在这期间GD 的值减小较快，这在图2（e）中GD 的收敛曲线体现出来；40次迭代到70次迭代，α0的值稳定在1.3 左右，算法处在收敛期，在这期间GD 的值缓慢减小到数量级10-4附近，表明搜索达到全局Pareto前沿，这在图1（e）中体现为动态自适应变化α0下的IMOCS达到了全局Pareto前沿，而固定α0下的IMOCS陷入了局部Pareto前沿；70次迭代以后，α0的值逐渐减小，在120次以后变为设定的最小值0.1，算法已进入停滞期，此后GD 的值稳定在数量级10-5附近，不再有明显的变化.

4.4.2 IMOCS与MOCS的性能比较分析 为了验证IMOCS算法的有效性，本文将其与MOCS的性能进行对比分析.Yang 等［10］给出了MOCS 在n＝50，MaxIter＝500时5个测试实例的GD值，本文计算IMOCS在相同条件下的GD 值，将2种算法的实验结果列于表3.从表3中可知，IMOCS所求GD值都小于MOCS，说明IMOCS性能好于MOCS.4.4.3 IMOCS 与NSPSO 的 性 能 比 较 分 析 Li［21］在2003年提出了基于非支配排序的粒子群优化算法（NSPSO）算法来解决多目标优化问题，算法主要基于非支配排序和小生境技术.为了验证IMOCS算法的有效性，本文将其与NSPSO 的性能进行对比分析.Li［21］给出了NSPSO 在n＝200，MaxIter＝100时4个测试实例的测试结果，本文给出了IMOCS在相同条件下的测试结果.如表4所示为4个测试实例P＊与P 之间的GD 的平均值和方差δ2，如表5所示为P＊的Δ 平均值和方差δ2.

表（5）为IMOCS和NSPSO 所求多样性均值与方差，由表5可知，IMOCS所求Δ 都小于NSPSO，表明IMOCS所求的Pareto前沿多样性更好，而且其偏差较小，进一步说明IMOCS的稳定性.

4.4.4 IMOCS与NSGA-II的性能比较分析 为了验证IMOCS算法的有效性，本文将其与NSGAII的性能进行对比分析.Deb［23］在2002 对NSGA进行改进，提出了NSGA-II，但并未给出实验分析.Yang等［10］给出了NSGA-II在n＝50，MaxIter＝500时5个测试实例的GD值，本文计算IMOCS在相同条件下的GD 值，将2 种算法的实验结果列于 表6.从 表6 中 可 知，IMOCS 所 求GD 值 都 小 于NSGA-II，说明IMOCS性能好于NSGA-II.

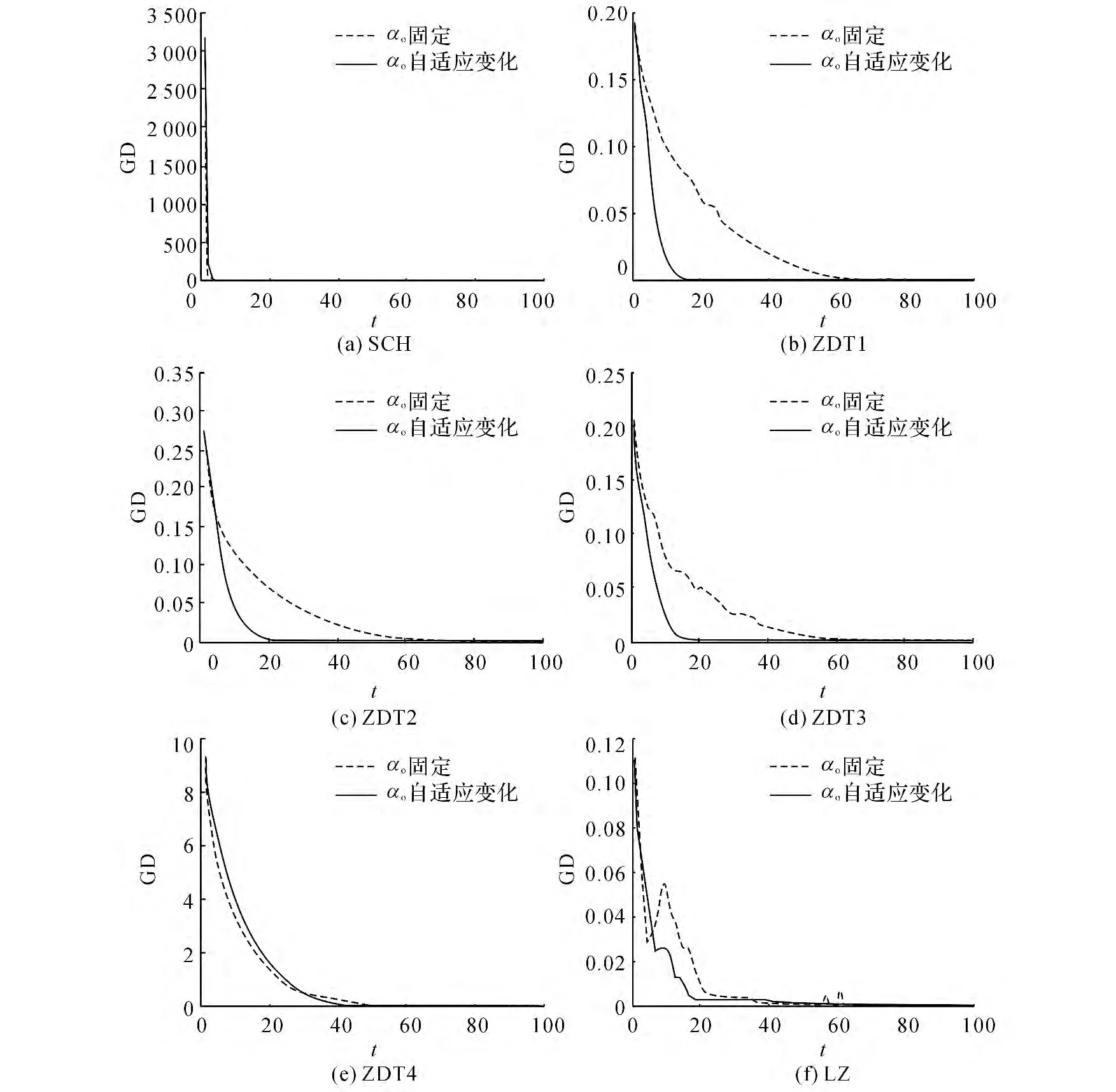
图2 6个测试实例的GD收敛曲线Fig.2 GD convergence curves of six test instances

表3 IMOCS与MOCS所求的GD值Tab.3 GD for IMOCS and MOCS

表4 IMOCS与NSPSO 所求的GD均值和方差Tab.4 Mean and variance of GD for IMOCS and NSPSO

表5 IMOCS与NSPSO 所求多样性的均值和方差Tab.5 Mean and variance of diversity for IMOCS and NSPSO

表6 IMOCS与NSGA-II所求的GD值Tab.6 GD for IMOCS and NSGA-II

图3 ZDT4中α0 的变化曲线Fig.3 Variation curve ofα0for ZDT4

5 结 语

通过对MOCS算法的2点改进：使用动态自适应的步长控制量α0及基于层级和拥挤度距离选择种群，本文提出了IMOCS算法.在测试实例SCH、ZDT 系列和LZ 上进行性能测试，研究了α0对IMOCS 寻优效果的影响，并与MOCS，NSPSO，NSGA-II进行比较.结果表明动态自适应变化α0下的IMOCS所求Pareto前沿的广义距离和多样性都优于MOCS和NSPSO，而且动态自适应变化的α0能使IMOCS 收敛速度更快、求解更加稳定.IMOCS中非支配集排序算法是不受目标数量和决策变量限制的，针对2个目标以上的多目标优化问题，同样能够为每个个体计算其层级和拥挤度距离，而广义距离GD 和种群多样性Δ 的计算方法由其定义可知是可以随目标的数量拓展的，在后续研究中，将研究2个目标以上的多目标优化问题.

（

）：

［1］YANG X S，DEB S.Cuckoo search via Lévy flights［C］∥World Congress on Nature ＆Biologically Inspired Computing.NaBic：IEEE Publications，2009：210-214.

［2］FISTER J I，YANG X S，FISTER D，et al.Cuckoo search：A brief literature review［M］.London：Springer International Publishing，2014：49-62.

［3］YANG X S，DEB S.Cuckoo search：recent advances and applications［J］.Neural Computing and Applications，2014，24（1）：169-174.

［4］GHERBOUDJ A，LAYEB A，CHIKHI S.Solving 0-1 knapsack problems by a discrete binary version of cuckoo search algorithm［J］.International Journal of Bio-Inspired Computation，2012，4（4）：229-236.

［5］OUAAARAB A，AHIOD B，YANG X S.Discrete cuckoo search algorithm for the travelling salesman problem ［J］.Neural Computing and Applications，2014，24（7／8）：1659-1669.

［6］LI Xiang-tao，WANG Jia-nan，YIN Ming-hao.Enhancing the performance of cuckoo search algorithm using orthogonal learning method［J］.Neural Computing and Applications，2014，24（6）：1233-1247.

［7］王李进，尹义龙，钟一文.逐维改进的布谷鸟搜索算法［J］.软件学报，2013，24（11）：2687-2698.WANG Li-jin，YIN Yi-long，ZHONG Yi-wen.Cuckoo search algorithm with dimension by dimension improvement［J］.Journal of Software，2013，24（11）：2687-2698.

［8］SRIVASTAVA P R，KHANDELWAL R，KHANDELWAL S.Automated test data generation using cuckoo search and tabu search（CSTS）algorithm ［J］.Journal of Intelligent Systems，2012，21（2）：195-224.

［9］胡欣欣，尹义龙.求解函数优化问题的合作协同进化布谷鸟搜索算法［J］.模式识别与人工智能，2013，26（11）：1041-1049.HU Xin-xin，YIN Yi-long.Cooperative co-evolutionary cuckoo search algorithm continuous function optimization poblems［J］.Pattern Recognition and Artificial Intelligence，2013，26（11）：1041-1049.

［10］YANG X S，DEB S.Multi-objective cuckoo search for design optimization［J］.Computers ＆ Operations Research，2011，40（6）：1616-1624.

［11］LAYEB A，LAHOUESNA N，KIRECHE B.A multiobjective binary cuckoo search for bicriteria knapsack problem［J］.International Journal of Information Engineering ＆Electronic Business，2013，5（4）：8-15.

［12］CHANDRASEKARAN K，SIMON S P.Multi-objective scheduling problem：Hybrid approach using fuzzy assisted cuckoo search algorithm ［J］.Swarm and Evolutionary Computation，2012，5（1）：1-16.

［13］BÄCK T.Evolutionary algorithms in theory and practice：Evolution strategies，evolutionary programming，genetic algorithms ［M］.Oxford：Oxford University Press，1996：161-164.

［14］张永韡，汪镭，吴启迪.动态适应布谷鸟搜索算法［J］.控制与决策，2014，29（4）：617-622.ZHANG Yong-wei，WANG Lei，WU Qi-di.Dynamic adaptation cuckoo search algorithm ［J］.Control and Decision，2014，29（4）：617-622.

［15］SRINIVAS N，DEB K.Multi-objective optimization using non-dominated sorting in genetic algorithms［J］.Evolutionary computation，1994，2（3）：221-248.

［16］DEB K，PRATAP A，AGARWAL S，et al.A fast and elitist multi-objective genetic algorithm：NSGA-II［J］.Evolutionary Computation，IEEE Transactions on，2002，6（2）：182-197.

［17］SCHAFFER J D.Multiple objective optimization with vector evaluated genetic algorithms［C］∥Proceedings of the 1st international Conference on Genetic Algorithms.New Jersey：L.Erlbaum Associates Inc，1985：93-100.

［18］ZITZLER E，THIELE L.Multi-objective evolutionary algorithms：a comparative case study and the strength Pareto approach［J］.Evolutionary Computation，IEEE Transactions on，1999，3（4）：257-271.

［19］ZITZLER E，DEB K，THIELE L.Comparison of multi-objective evolutionary algorithms：Empirical results［J］.Evolutionary Computation，2000，8（2）：173-195.

［20］ZHANG Qing-fu，LI Hui.MOEA／D：A multi-objective evolutionary algorithm based on decomposition［J］.Evolutionary Computation，IEEE Transactions on，2007，11（6）：712-731.

［21］LI Xiao-dong.A non-dominated sorting particle swarm optimizer for multi-objective optimization［C］∥Genetic and Evolutionary Computation—GECCO 2003.Chicago：Springer Berlin Heidelberg，2003：37-48.

［22］LI Hui，ZHANG Qing-fu.Multi-objective optimization problems with complicated Pareto sets，MOEA／D and NSGA-II［J］.Evolutionary Computation，IEEE Transactions on，2009，13（2）：284-302.

［23］DEB K Multi-objective optimization using evolutionary algorithms［M］.Chichester：John Wiley ＆ Sons，2001：320-332.