HU Lin(胡琳)，WU Qiang(吴强)，XU Qing－cui(徐青翠)，ZHANG Zu－jin(张祖锦)，LIHuacan(李华灿)

1 School of Science，Jiangxi University of Science and Technology，Ganzhou 341000，China

2 Forestry and Environmental Institute，Jiangxi Environmental Engineering Vocational College，Ganzhou 341000，China

3 School of Resource and Safety Engineering，Central South University，Changsha 410075，China

4 Department of Information Engineer，Jiangxi University of Science and Technology，Nanchang Campus，Nanchang 340000，China

5 School of Mathematics and Computer Sciences，Gannan Normal University，Ganzhou 341000，China

Numerical Analysis of Balanced Methods for the Impulsive Stochastic Differential Equations

HU Lin(胡琳)1*，WU Qiang(吴强)2，3，XU Qing－cui(徐青翠)4，ZHANG Zu－jin(张祖锦)5，LIHuacan(李华灿)1

1 School of Science，Jiangxi University of Science and Technology，Ganzhou 341000，China

2 Forestry and Environmental Institute，Jiangxi Environmental Engineering Vocational College，Ganzhou 341000，China

3 School of Resource and Safety Engineering，Central South University，Changsha 410075，China

4 Department of Information Engineer，Jiangxi University of Science and Technology，Nanchang Campus，Nanchang 340000，China

5 School of Mathematics and Computer Sciences，Gannan Normal University，Ganzhou 341000，China

Positive results are proved here about the ability of balanced methods to reproduce the mean square stability of the impulsive stochastic differential equations．It is shown that the balanced methods with strong convergence can preserve the mean square stability with the sufficiently small stepsize．Weak variants and their mean square stability are also considered．Several numerical experiments are given for illustration and show that the fully implicitmethods are superior to those of the explicitmethods in terms of mean-square stabilities for relatively large stepsizes especially．

impulsive stochastic differential equation;balancedmethod; convergence;mean square stability

Introduction

Stochastic model has come to play an important role in many branches of science and engineering.Impulsive effects exist w idely in many evolution processes in which states are changed abruptly at certain moments of time，involving such fields as biology，econom ics，medicine，mechanics and electronics(see Refs.［1－2］and reference therein). However，in addition to impulsive effects，stochastic effects likew ise exist in real systems.It is well known that a lot of dynamic systems have variable structures subject to stochastic abrupt changes，whichmay result from abrupt phenomena such as stochastic failures and repairs of the components，changes in the interconnections of subsystems，and sudden environment changes.In recent years，the stability investigation of the impulsive stochastic differential equations has been discussed by several authors［3－7］.

Unfortunately，the stochastic differential equations (including the impulsive stochastic differentialequations)rarely have explicit solutions.Thus，appropriate numerical methods are needed to apply in practice and study their properties.The numerical analysis of the stochastic differential equations iswell studied［8－16］and of the impulsive stochastic differential equations is discussed in Refs.［17－22］.

However，in these papers，it is already known that the numericalmethods for impulsive stochastic differentialequations are explicit or semi－implicit.Semi－implicit methods are well adapted for stiff systemswith small stochastic noise intensity or additive noise.But in those cases in which the stochastic part plays an essential role in the dynam ics，e．g．，as it iswith large multiplicative noise，the application of fully implicit methods also involving implicit stochastic terms is unavoidable.One of the most important fully implicit numerical methods was the balanced implicit method，which was first proposed by M ilstein，Platen，and Schurz［24］.In 2006，Alcock and Burrage［23］obtained the region of the asymptotic stability and themean square stability of balanced methods for the stochastic differential equations(SDEs).Furthermore，Tan，Gan and Wang［25］investigated the convergence and stability of balanced methods for the stochastic delay differential equations (SDDEs).Lately，Wang and Liu［26］discussed the convergence and stability of the split－step backward balanced M ilstein methods for SDEs.Hu etal．［27－28］investigated the convergence and stability of the balanced methods for SDEs with jumps. Moreover，Hu and Gan［29］proved the order of themean square convergence of the balanced methods for the neutral SDDEs (NSDDEs)with jumps is 1/2.

Consider the following scalar linear impulsive stochastic differential equation.

where x(t－)denotesx0≠0with probability one，thecoefficients a，b∈，γ(t):N→/{－1}，γ(1)，γ(2)，…，are independent random variables.Here，W(t)is a scalar Brownianmotion defined on an appropriate complete probability space(Ω，F，{Ft}t0，P)，with a filtration{Ft}t0satisfying the usual conditions(i．e．，it is increasing and right－continuous while F0contains all P－null sets).

It is known that Eq.(1)has the analytic solution［21］

where［t］denotes the greatest integer less than or equal to x.

Regarding stability analysis，Liu et al.［21］have given a sufficient condition which guarantees the mean square stability of the analytical solution.Furthermore，they have studied the mean square stability of the sem i－implicit Euler method. However，there are few stability results of balancedmethods for the impulsive stochastic differential equations.This paper aims to investigate the convergence and the mean square stability of balanced methods.

1 Mean Square Stability of Strong Balanced Methods

Define a mesh with uniform step h=and m is an integer.We define the strong balanced implicitmethods for the

simulation of the solution x(t)of Eq.(1)as follows.

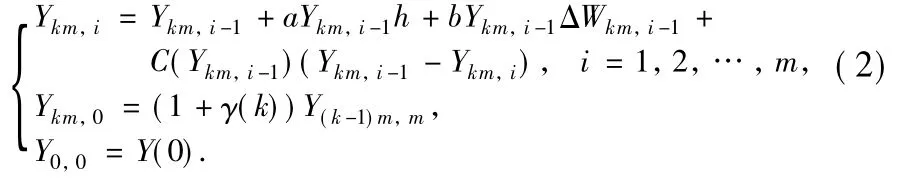
Here Ykm，iis an approximation to x(tkm，i)with tkm，i=k+ih(0≤i≤m)，Y(0)=x(0)，Ykm，m≈x((k+1)－)=andΔWkm，i－1=W(tkm，i)－W(tkm，i－1)．Here C(Ykm，i－1)is given by

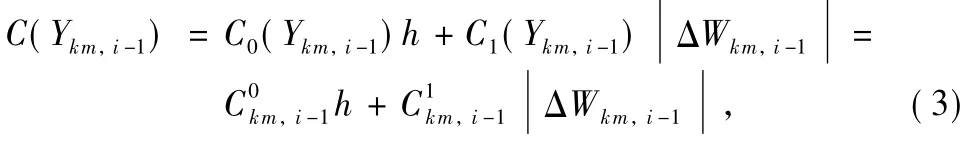
We always suppose that the C0and C1satisfy some conditions.

Assum ption 1For any real numberswhereh for all step sizes h considered，1+α0C0(x)+ α1C1(x)has an inverse and satisfies the condition

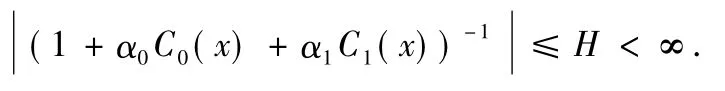
Here H is a positive constant.

The follow ingLemma 1gives a sufficient condition for the mean square stability of system(1).

Lemma 1［21］Let M=M＜+∞，if

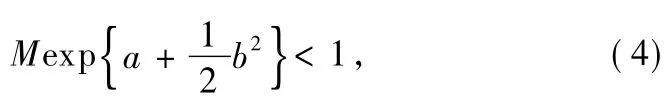
then the analytic solution x(t)of the system(1)ismean square stable，that is，Especially，if γ(j)=γ，∀j∈，then the analytic solution x(t)ismean square stable if and only if

Theorem 1UnderAssumption 1，the balanced methods Formula (2)for Eq.(1)are convergent with order 1/2 in the mean square sense.

ProofThroughout this proof，we use J1，J2，J3，and J4to denote generic constants，independent of h.We denote x(tkm，i)=x(k+ih)，x(tkm，m)=x((k+1)－)，mh=1，i= 0，1，…，m－1，k=0，1，2，…．The system(1)is a stochastic differential equation on the interval［k，k+1)(k= 0，1，2，…)，thus，using Theorem 2.1 with u(·)=0 in Ref.［27］，it is not difficult to find that

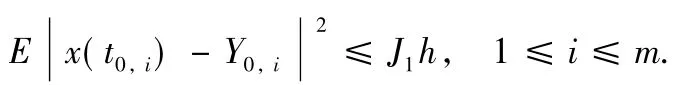
Use Eqs.(1)and(2)and yield

By Eq.(49)in Ref.［27］and the above equation，we find that

Using the same arguments as above，we can derive

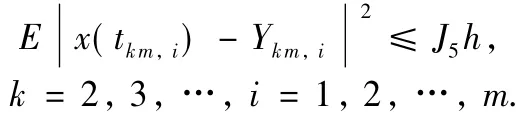
We obtain the desired results.

Theorem 1gives a sufficient condition for themean square stability of system(1).

Definition 1A numerical method is said to be mean square stable if under condition(1)，for given parameters a，b and stepsize h，the numerical solutions Ynsatisfies，which is generated by the application of themethod to system(1)

for any Y0.

The follow ing theorem will show themean square stability of the balanced methods.

Theorem 2Under the condition(1)andAssumption 1，the strong balanced methods(2)are mean square stable for the linear system(1).

ProofNotice that if C0and C1satisfyAssumption 1，the numericalmethods(2)are well－defined and we arrive at

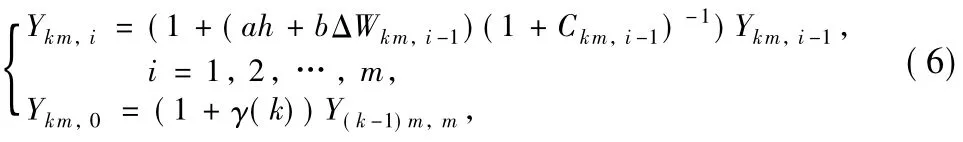
Noting Y(k－1)m，iis Ft(k－1)m，i－measurable，γ(1)，γ(2)，…，Y0，andΔWiare independent each other.Squaring and taking expectation on both sides of the first equation in Eq.(6)，we show that

By the properties of the Brownianmotion，we find that

Lettingξbe independent standard normal random variable，we know that

We w rite the third term at the right－hand side of Eq.(9)as the following formAssum ption 1and properties ofΔWkm，jgive

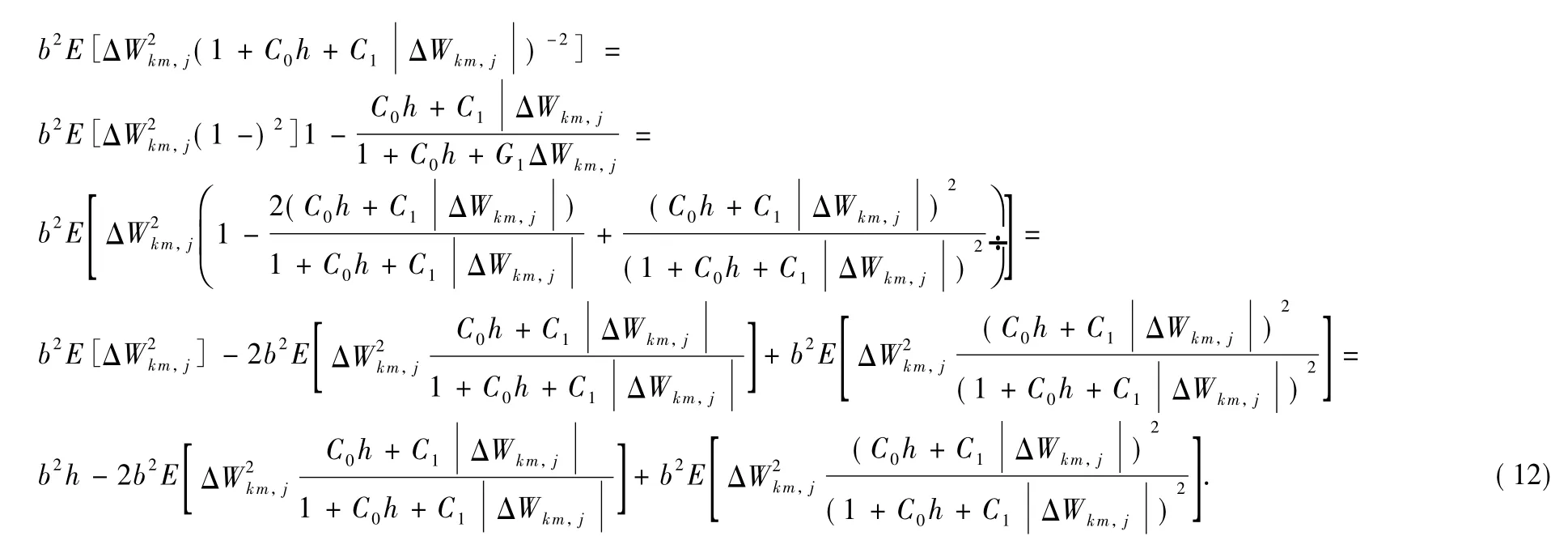
and

Insert Eqs.(13)－(14)into Eq.(12)and yield

Similarly，we have

and

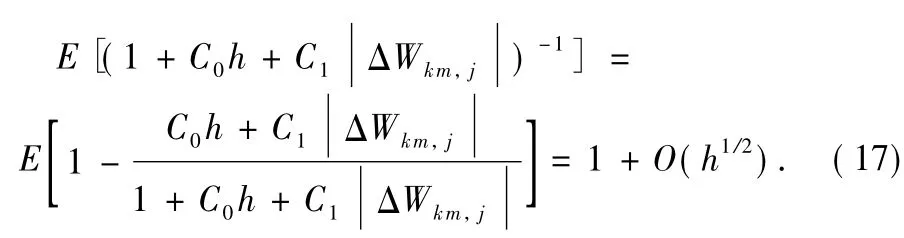
Combine Eqs.(10)－(11)and(15)－(17)with Eq.(9) and yield

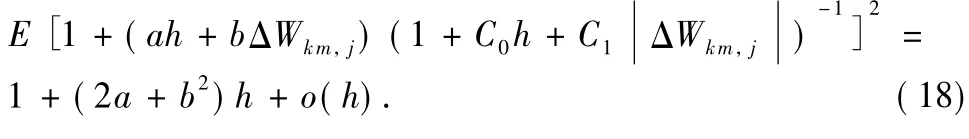
Using a similar approach as before，one can derive

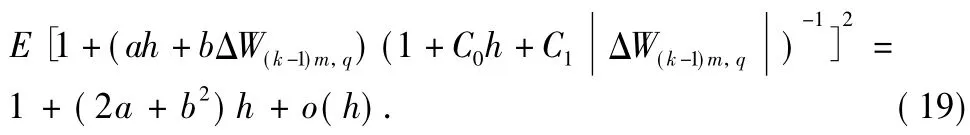
Insert Eqs.(18)and(19)into Eq.(8)and yield

秦明月简直不敢相信线索来得如此简单与突然。边峰则已经举起相机对着车子一通猛拍了。秦明月不放心地说：“你们会不会记错了，这种车其实很普通的。”

From thiswe see that limn→∞E(Yn)2=0 if and only if

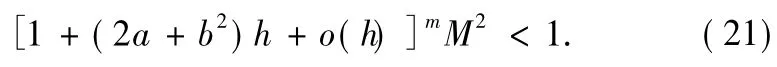
For all sufficiently small stepsize h，we can deduce from

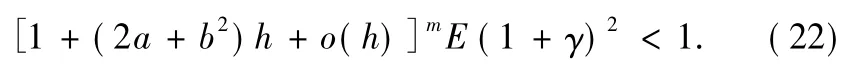
For all sufficiently small stepsize h，Eq.(22)becomes

This completes the proof.

2 Mean Square Stability of Weak Balanced Methods

It is not difficult to prove that

Themain theorem in this section is given as follows.

Theorem 3Under the condition(1)andAssumption 1，the weak balanced methods of Eq.(23)aremean square stable for the linear system(1).

ProofBy Eq.(23)，we find that

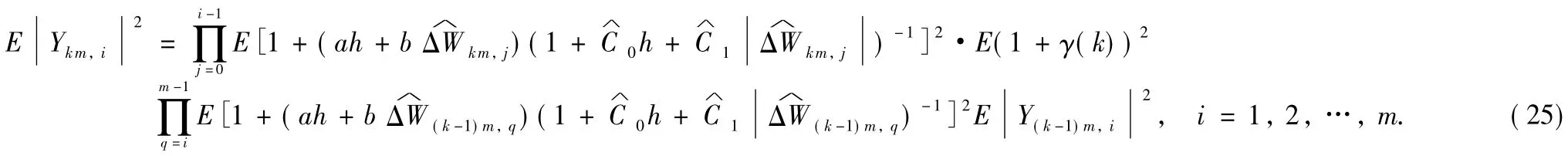
The properties of the Brownianmotion give

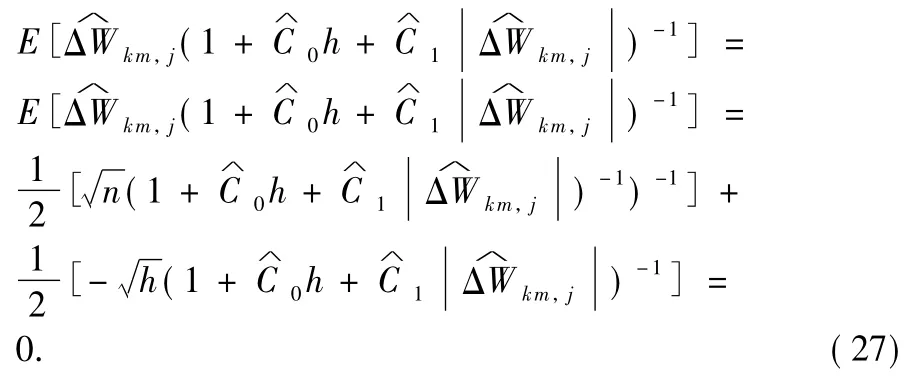
Similarly

It is not difficult to find that

using Taylor expansion

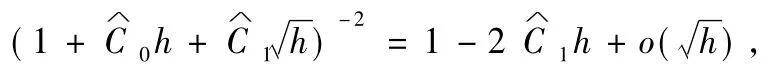
thus，Eq.(29)becomes

Similarly，we have

and

Substitute Eqs.(27)－(28)and(30)－(32)into Eq.(26) and yield

In a sim ilar way as before，one can derive

Combine Eqs.(33)－(34)with Eq.(25)and yield

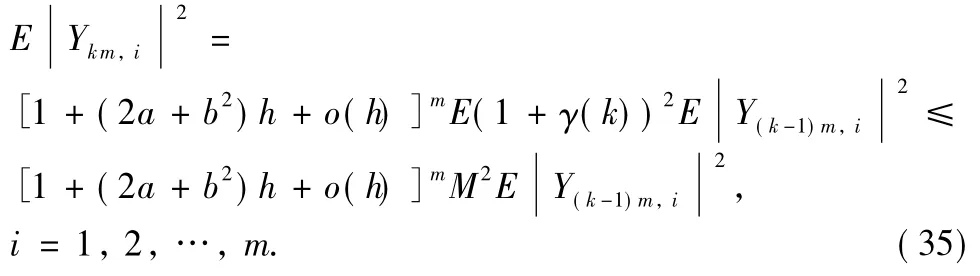
We can derive the desired assertion using the same arguments inTheorem 2.

3 Numerical Experiments

Consider the scalar linear equation

For simplicity，in all the numericalexperimentswe choose C0= 1 and C1=1.Next，we show the convergence of the strong balanced methods(2).We illustrate the convergence via the two follow ing examples.Example 1:a=－3，b=0.3，andγ =18;Example 2:a=－0.5，b=0.1，andγ=0.6.We use xtand Ynto denote the analytic and the numerical solutions of the system(1)，respectively.The mean square errorsεall measured at fixed terminal time T=100，are estimated in the follow ing way.A set of 20 blocks each containing 100 outcomes(ωij:1≤i≤20，1≤j≤100)are simulated and for each block the estimator

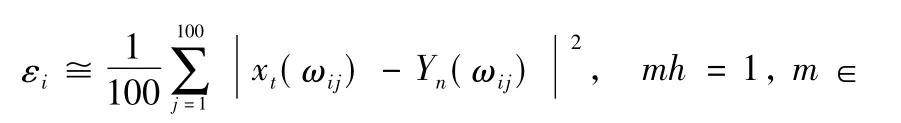
is formed.In Table 1，εdenotes the mean of this estimator，which is self－estimatied with four different stepsize h in the usual way: It is not difficult to find that the mean square errorεbecomes smaller when the stepsize h decreases. Thus our result concerning convergence for the balanced implicit methods is verified.

Table 1 The global errors of the strong balanced methods

To verify our result concerning mean square stability for the balanced implicit methods，we compare the numerical approximations of the Euler－Maruyama methods which are explicitmethods versus the balanced methodswhich are implicit methods to show the balanced implicit methods adm it better stability property.In Figs.1－8，the star lines and the solid lines represent the solutions produced by the balancedmethod and the Euler－Maruyama method，respectively.All the graphs are drawn with the vertical axis scaled logarithmically.

Consider the strong Euler－Maruyamamethod

and the weak Euler－Maruyamamethod

To verify our result concerning strongmean square stability for the strong balanced method and the strong Euler－Maruyama method，we illustrate them via the four follow ing examples.

Example 3:a=－5，b=1，γ=5．

Example 4:a=－2，b=0．1，γ=－0．5．

Example 5:a=－3，b=2．2，γ=－0．6．

Example 6:a=－1．1，b=－1．4，γ=0．1．

The values of the coefficients in Examples 3－6 satisfy the condition(5)，and thus the system(36)ismean square stable. Applying the strong balanced implicit methods(2)and the strong Euler－Maruyamamethod(37)to Examples3－6，we plot the numerical solutions in Figs.1－4.In Fig.1，the behavior of the strong balanced implicitmethods for h=，h=，and h =are clearly consistentwith mean square stability，whereas the strong Euler－Maruyama method is mean－square stable only on h=and h=Figure 2 shows that both kinds of methods aremean square stable on h=and h=.For some larger stepsize h=，the strong balanced implicitmethods are still stable，however，the solution produced by the strong Euler－Maruyamamethod becomes very large and is unstable.From Fig.3，one can easily observe that the two numerical simulations are stable for small stepsize h=0.05 and 0.25.But when the stepsize h increases to 1.5，the strong Euler－Maruyamamethod becomes unstable whereas the strong balanced implicitmethods are still stable.For Example 6，we can obtain the similar observation as shown in Fig.4.

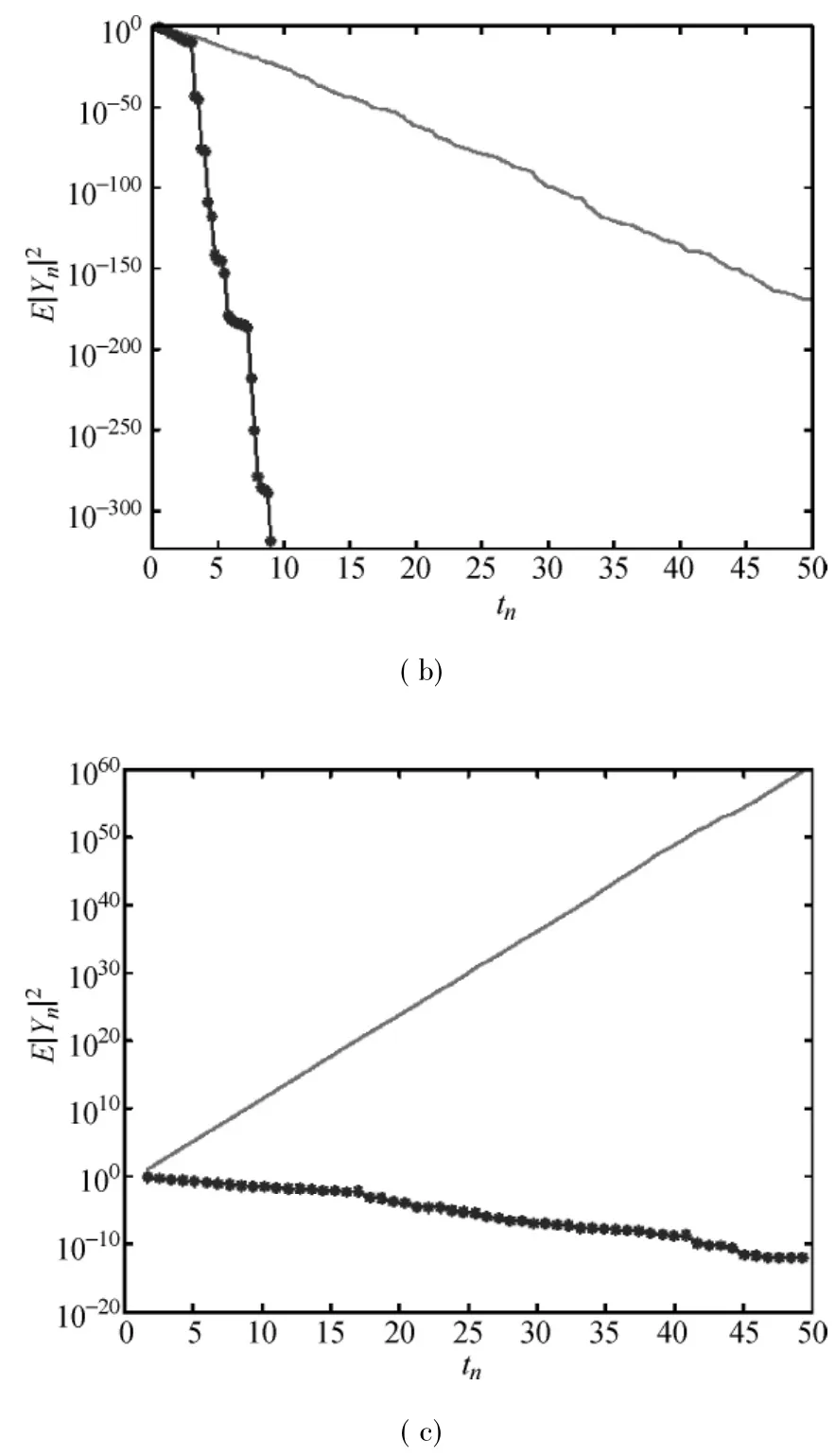
Fig.1 Strong balanced methods and strong Euler－Maruyamamethod for Example 3:(a)h=，(b)h=，and(c)h=

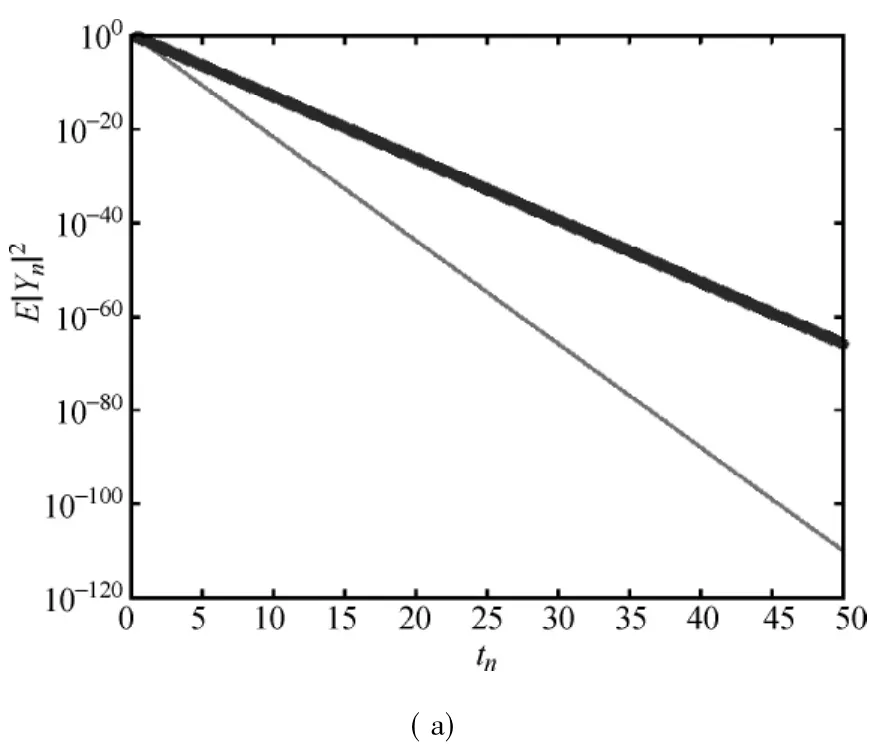
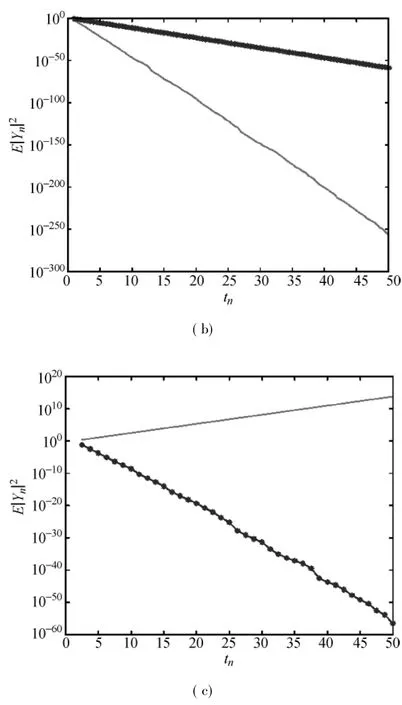
Fig.2 Strong balanced methods and strong Euler－Maruyama method for Example 4:(a)h=，(b)h=，and(c)h=

Fig.3 Strong balanced methods and strong Euler－Maruyamamethod for Example 5:(a)h=，(b)h=，and(c)h=

Fig.4 Strong balanced methods and strong Euler－Maruyamamethod for Example 6:(a)h=，(b)h=，and(c)h=2

The graphs clearly show that these two kinds of strong numericalmethods are stable with small stepsize，but for large stepsize h，the strong balanced implicitmethods are still stable whereas the strong Euler－Maruyamamethod becomes unstable. The numerical results in Figs.1－4 show that，the strong balancedmethods possess better stability properties and have less restriction on the stepsize.

In the follow ing，wewill show themean square stability of the weak numerical methods.We consider the follow ing examples.

Example 7:a=－4，b=－1，γ=8．

Example 8:a=－1，b=－1．2，γ=0．2．Example 9:a=－2，b=0．5，γ=4．

Example 10:a=－0．6，b=0．8，γ=－0．5．

Note that the parameters in these four examples satisfy the condition(5)，and thus both solutions of the system(36)are mean square stable.Applying the weak balanced implicit methods(23)and the weak Euler－Maruyama method(38)to Examples 7－10，we plot the numerical solutions in Figs.5－8. In Fig.5，the behavior of the weak balanced implicitmethods for h=，h=，and h=is clearly consistentwith mean square stability，whereas the weak Euler－Maruyama method is mean－square stable only on h=，and h=.In Fig.6，we find that the weak Euler－Maruyama method becomes unstable whereas the weak balanced methods still successfully reproducethe mean square stability of the test problem even for large stepsize h=.In Fig.7，the weak Euler－Maruyama method guarantees stability on h=and，but fails to preserve stability on larger stepsize h=2.However the weak balanced methods ensure their good performance even the stepsizes h increase to 2.From Fig.8，one can observe a sim ilar effect brought by increasing the stepsize.

Fig.5 Weak balanced methods and weak Euler－Maruyama method for Example 7:(a)h=，(b)h=，and(c)h=

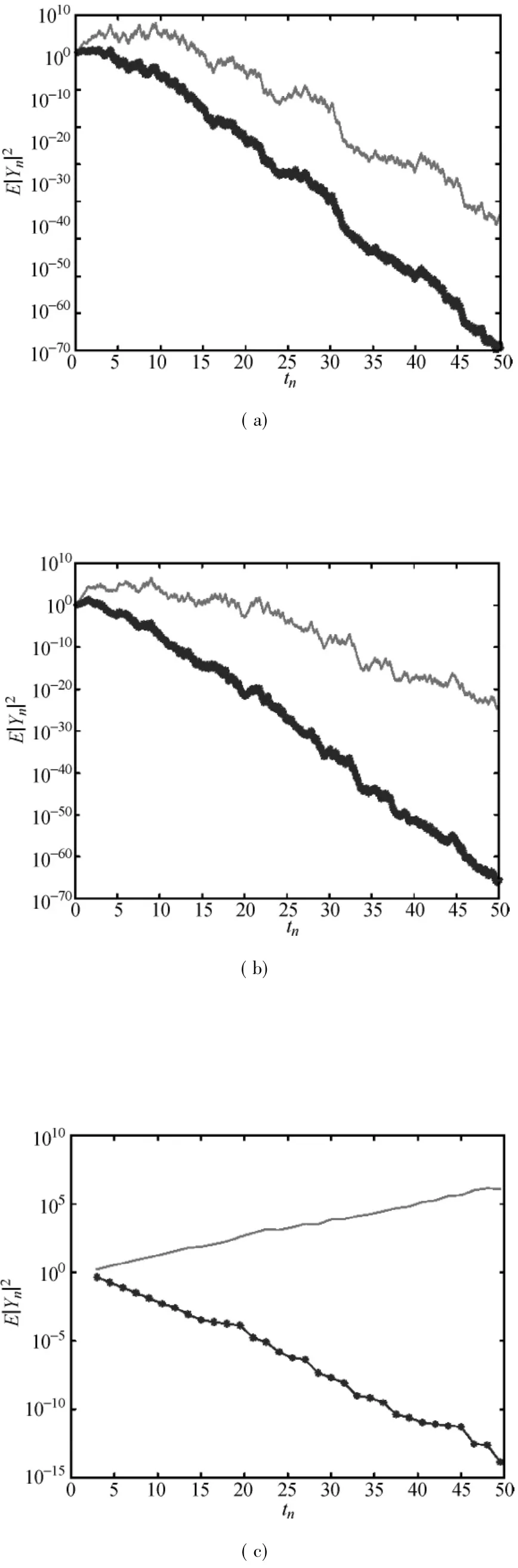
Fig.6 Weak balanced methods and weak Euler－Maruyama method for Example 8:(a)h=，(b)h=，and(c)h=

Fig.7 Weak balanced methods and weak Euler－Maruyama method for Example 9:(a)h=，(b)h=，and(c)h=2

Fig.8 Weak balanced methods and weak Euler－Maruyama method for Example10:(a)h=，(b)h=，and(c)h=

From above，one can see that for large stepsize h，the weak balanced implicit methods are stable whereas the weak Euler－Maruyamamethod is unstable.Hence the weak balanced methods also allow larger range of the stepsize than the weak Euler－Maruyamamethod.

The numerical results in Figs.1－8 show that，to preserve stability the balanced methods allow for larger range of thestepsize than the Euler－Maruyama methods.The balanced implicitmethods adm it better stable properties than the Euler－Maruyama method with the same stepsize.Overall，they are consistentwith the established results.

4 Conclusions

In this work，we have examined the convergence and the mean－square stability of the balanced methods for the pulse stochastic differential equations.It is shown that the balanced implicitmethods give strong convergence rate，at least1/2.The forgoing results show the mean square stability of strong balanced methods and weak balanced methods for the pulse stochastic differential equations.The theory result and the numerical experiment show that balanced methods which have the implicit diffusion term are indeed the superior schemes for relatively large stepsizes and admit better stability property than the Euler－schememethod which has the explicit diffusion term.

［1］Samoilenko A M，Perestyuk N A.Impulsive Differential Equations［M］.Singapore:World Scientific，1995.

［2］Nieto J J，Rodriguez－Lopez R.Boundary Value Problems for a Class of Impulsive Functional Equations［J］.Computers＆Mathematicswith Applications，2008，55(12):2715－2731.

［3］Xu W，Niu Y J，Rong H W，et al.p－Moment Stability of Stochastic Impulsive Differential Equations and Its Application in Impulsive Control［J］.Science in China Series E:Technological Sciences，2009，52(3):782－786.

［4］Yang J，Zhong SM，Luo W P.Mean Square Stability Analysis of Impulsive Stochastic Differential Equations with Delays［J］. Journal of Computational and Applied Mathematics，2008，216 (2):474－483.

［5］Yang Z G，Xu D Y.Mean Square Exponential Stability of Impulsive Stochastic Difference Equations［J］.Applied Mathematics Letters，2007，20(8):938－945.

［6］Wu K N，Ding X H.Stability and Stabilization of Impulsive Stochastic Delay Differential Equations［J］.Mathematical Problems in Engineering，2012，2012:Article ID 176375.DOI: 10.1155/2012/176375.

［7］Bao JH，Hou Z T，Wang F X.Exponential Stability in Mean Square of Impulsive Stochastic Difference Equations with Continuous Time［J］.Applied Mathematics Letters，2009，22 (5):749－753.

［8］Wu F K，Mao X R.Numerical Solutions of Neutral Stochastic Functional Differential Equations［J］.Siam Journalon Numerical Analysis，2008，46(4):1821－1841.

［9］Higham D J，Mao X R，Yuan C G.Preserving Exponential Mean－Square Stability in the Simulation of Hybrid Stochastic Differential Equations［J］.Numerische Mathematik，2007，108 (2):295－325.

［10］Jiang F，Shen Y，Hu JH.Stability of the Split－Step Backward Euler Scheme for Stochastic Delay Integro－Differential Equations with Markovian Switching［J］.Communications in Nonlinear Science and Numerical Simulation，2011，16(2):814－821.

［11］Hu P，Huang C M.Stability of Stochasticθ－Methods for Stochastic Delay Integro－differential Equations［J］.International Journal of Computer Mathematics，2011，88(7):1417－1429.

［12］Rathinasamy A，Balachandran K.T－Stability of the Split－Stepθ－Methods for Linear Stochastic Delay Integro－Differential Equations［J］.Nonlinear Analysis:Hybrid Systems，2011，5(4):639－646.

［13］Yin ZW，Gan S Q，Li R D.General Modified Split－Step Balanced Methods for Stiff Stochastic Differential Equations［J］. Jounal of Donghua University:English Edition，2013，30(3): 189－196.

［14］Tretyakov M V，Zhang Z Q.A Fundamental Mean－Square Convergence Theorem for SDEs with Locally Lipschitz Coefficients and Its Applications［J］.SIAM Journal on Numerical Analysis，2013，51(6):3135－3162.

［15］Cao W R，Zhang Z Q.On Exponential Mean－Square Stability of Two－Step Maruyama Methods for Stochastic Delay Differential Equations［J］.Journal of Computational and Applied Mathematics，2013，245(1):182－193.

［16］Jing F，Shen Y，Liao X X.A Note on Stability of the Split－Step Backward Euler Method for Linear Stochastic Delay Integro－Differential Equations［J］.Journal of Systems Science and Complexity，2012，25(5):873－879.

［17］Wu S J.The Euler Scheme for Random Impulsive Differential Equations［J］.Applied Mathematics and Computation，2007，191(1):164－175.

［18］Wu S J，Han D.Algorithmic Analysis of Euler Scheme for a Class of Stochastic Differential Equations with Jumps［J］. Statistics＆Probability Letters，2007，77(2):211－219.

［19］Li B，Li D S，Xu D Y.Stability Analysis for Impulsive Stochastic Delay Differrential Equationswith Markovian Sw itching［J］.Journal of the Franklin Institute，2013，350(7):1848－1864.

［20］Zhao G H，Song M H，Liu M Z.Exponential Stability of Euler－Maruyama Solutions for Impulsive Stochastic Differential Equations with Delay［J］.Applied Mathematics and Computation，2010，215(9):3425－3432.

［21］Liu M Z，Zhao G H，Song M H.Stability of the Semi－implicit Euler Method for a Linear Impulsive Stochastic Differential Equation［J］.Discrete and Continuous Dynamical Systems Series B:Applications Algorithms，2011，18(2):123－134.

［22］Wu K N，Ding X H.Convergence andStability of Euler Method for Impulsive Stochastic Delay Differential Equations［J］. Applied Mathematics and Computation，2014，229:151－158.

［23］Alcock J，Burrage K.A Note on the Balanced Method［J］.BIT Numerical Mathematics，2006，46(4):689－710.

［24］M ilstein G N，Platen E，Schurz H.Balanced ImplicitMethods for Stiff Stochastic Systems［J］.SIAM Journal on Numerical Analysis，1998，35(3):1010－1019.

［25］Tan Y X，Gan S Q，Wang X J.Mean－Square Convergence and Stability of Balanced Method for Stochastic Delay Differential Equations［J］.Mathematica Numerica Sinica，2011，33(1):25－36.(in Chinese)

［26］Wang P，Liu Z X.Split－Step Backward Balanced M ilstein Methods for Stiff Stochastic Systems［J］.Applied Numerical Mathematics，2009，59(6):1198－1213.

［27］Hu L，Gan S Q.Convergence and Stability of the Balanced Methods for Stochastic Differential Equations with Jumps［J］. International Journal of Computer Mathematics，2011，88(10): 2089－2108.

［28］Hu L，Gan S Q，Wang X J.Asymptotic Stability of Balanced Methods for Stochastic Jump－Diffusion Differential Equations［J］.Journal of Computational and Applied Mathematics，2013，238:126－143.

［29］Hu L，Gan SQ.Mean－Square Convergence of Drift－ImplicitOne－Step Methods for Neutral Stochastic Delay Differential Equations with Jump Diffusion［J］.Discrete Dynamics in Nature and Society，2011，2011:Article ID 917892.DOI:10.1155/2011/ 917892.

O175;O24

A

1672－5220(2015)04－0626－10

date:2014－03－26

s:National Natural Science Foundations of China(Nos.11561028，11101101，11461032，11401267);Natural Science Foundations of Jiangxi Province，China(Nos.20151BAB201013，20151BAB201010，20151BAB201015)

*Correspondence should be addressed to HU Lin，E－mail:littleleave05@163.com